加权主成分距离聚类分析方法的有效性

韩 玉，党宏鹏，朱 猛

(东北电力大学 理学院，吉林 吉林 132012)

随着现代数据存储技术的发展，海量数据库的内在规律愈加复杂难辨.在对海量数据进行分类挖掘时，传统的聚类方法面临诸多的局限[1].事实上，某种聚类分析方法仅仅适用于分析数据中的某类规律，如果忽略模型的适用前提和聚类对象的具体特点，简单地套用传统聚类模型将难以取得理想的分类效果.关于如何解决传统聚类方法，处理现有海量数据问题，很多学者进行了很多有益的探讨.国内学者刘瑞元[2]定义了加权欧氏距离，并讨论了它的性质，并应用加权欧氏距离对2000年奥运金牌榜前10名的国家进行了加权聚类分析.在传统聚类分析的基础上，加权聚类分析方法考虑了指标之间重要性的差异，但没有考虑指标之间存在高度相关性的因素.王庆丰[3]采用主成分分析与聚类分析相结合的集成方法(即一般主成分聚类分析方法)将指标降维成若干相互独立的主成分因子[4]，进而以等权的主成分因子代替原始指标对我国各地区人口素质差异进行聚类分析.一般主成分聚类是在忽略主成分因子的特征权重的条件下进行聚类，虽然解决了指标之间的高度相关性，但又忽略了因子特征权重的影响，特征权重是对主成分因子进行赋权，再对赋权的主成分因子进行聚类，这样便加大了第一主成分对分类的影响，也会对分类的精度产生影响.

基于现有的聚类方法，本文基于已有聚类及主成分分析方法，提出一种新的聚类方法——加权主成分距离聚类方法.加权主成分距离聚类是按特征权重，对主成分因子进行赋权，这样可使各主成分的重要性保持着原有的比例关系.

1 已有聚类分析方法及不足

1.1 传统聚类方法及其不足

传统的聚类分析多是基于样本(指标)之间距离(相关系数)的亲疏关系进行分类[5～9]，相似性度量不但取决于指标之间的亲疏程度，而且依赖于指标重要性的内在差异.因此，用于构建聚类统计量的指标选择至为重要.传统的聚类算法要求描述样本的指标重要性相同，并且彼此独立，然而对于复杂的海量数据库，系统层次结构的指标体系中各指标重要性相差悬殊，指标之间不可避免地会有信息的重叠.如果对存有高度共线性的指标不加处理，直接聚类，那么聚类统计量将同类指标重复计算，过于放大共线性指标的作用，而淹没独立性指标的贡献，导致分类结果失真.应用传统聚类模型处理实际分类问题，为了克服指标体系的高度共线性，往往是定性分析指标之间的机理关系，再主观删除信息重叠的指标，这样以达到聚类指标彼此独立.例如通过专家打分赋予不同指标相应的权重，以体现指标重要性的差异.显然，定性地筛选指标和主观赋权，需要对每一指标的实际意义有深入的了解，并且要求分析者具有相关的领域知识和客观公正的赋权标准，这在实际应用中难以保证.

1.2 一般主成分聚类分析方法及其不足

主成分分析方法是降低数据空间维度的重要方法[10]，其分析结果是将原始错综复杂的指标体系通过线性变换转化为少数相互独立的主成分综合指标，并且要求低维主成分空间能够体现原始指标体系的绝大部分信息.一般主成分聚类分析方法，首先应用主成分分析克服原始指标之间的共线性影响，再用少数主成分代替原始指标进行聚类.值得肯定的是，主成分聚类克服了传统聚类模型不能处理指标之间高度共线性的不足，但应该注意到，不同主成分体现原始指标体系信息的能力(方差贡献率)往往相差悬殊，如果忽略不同主成分重要性的客观差异，不加区别地直接将主成分代替原始指标聚类，则必然会影响主成分聚类分析的准确性.

设F1，F2，，Fs(s≤p)为提取的主成分因子的列向量，其中Fi=(Fi1，，Fip).假设所提取主成分因子F1，F2，，Fs对应的特征值分别为λ1，λ2，，λs，且λ1≥λ2≥≥λs，

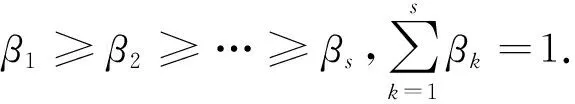
(1)

式中：dij(q)为样本Ii与Ij之间的距离，dij(q)越小(大)表示两样本接近程度越大(小).不难发现，该距离定义直接将主成分因子代替原始指标聚类，在实际运用时存在一个前提假设，即s个主成分因子对分类的重要性均相等，即主成分因子的特征权重β1=β2==βs.然而，由于提取主成分因子时已假设β1≥β2≥≥βs，因此，dij(q)样本距离定义的前提假设与主成分因子提取的前提假设相违背，采用等权的主成分因子代替原始指标直接进行聚类分析，便削弱了特征权重较大的第一主成分因子的重要性，同时放大了特征权重较小的其他主成分因子的重要性，从而导致一般主成分聚类分析方法的分类结果失真.

1.3 加权主成分聚类分析方法及其不足

借鉴主成分聚类分析思想，考虑主成分体现原始指标信息含量的差异性[11]，本文通过赋予各主成分相应的客观权重体现其重要程度的不同，从而定义加权主成分距离为分类统计量，定义第i个样本和第j个样本之间的加权主成分距离为

(2)

通过主成分分析的特征提取，加权主成分聚类分析既剔除了原始指标共线性的重叠信息，又体现了各主成分包含原始指标信息含量的差异.

显然在该距离的定义中，主成分因子Fk(k=1，2，3，，s)对距离dij(q)的权重实际可理解为

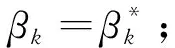
1.4 加权主成分距离的聚类分析方法

针对上述聚类分析方法在特定情形下的失真问题，本文提出加权主成分距离聚类分析方法.设为F1，F2，，Fs(sp)由p维指标向量X=(x1，x2，xp)提取的主成分因子列向量.假设所提取主成分因子F1，F2，，Fs对应的特征值分别为λ1，λ2，，λs，且为主成分因子Fk所对应的特征权重，于是有采用一般主成分聚类分析方法所定义的样本Ii与Ij之间的距离为

(3)

其中：与公式(2)不同的地方，公式(3)是按照主成分因子对应的权重对不同主成分因子下的距离进行加权，由此进行聚类分析.聚类距离的定义需要满足非负性、对称性和三角不等式，不难证明公式(3)满足上述三条性质.与现有聚类分析改进的研究成果相比，加权主成分距离聚类的核心优势在于，同时克服了经典聚类分析存在的两个典型缺陷：(1)通过主成分的特征提取，剔除了原始指标体系高度的重叠信息；(2)每一主成分的距离权重βk来源于原始指标数据，体现了不同主成分聚类效率的差异，并且对各主成分因子下的样本距离赋权，但没有改变各主成分因子对分类重要的比例关系，赋权准则客观合理.加权主成分距离聚类的具体步骤如下：

步骤 1：比较原始指标数据数量级和离散程度的差异，从而确定是采用标准化处理后的无量纲数据，还是采用非标准化的原始数据；

步骤 2：计算指标的相关系数矩阵、KMO检验与Bartlett球形检验值及显著性水平，以判断样本数据是否适宜进行主成分分析，如符合则进入步骤3；

步骤 3：进行主成分分析，计算相关系数矩阵或协方差矩阵的特征值和特征向量，以及各主成分因子的贡献率和累计贡献率，提取主成分因子，并结合因子载荷矩阵对所提取的主成分因子进行命名；

步骤 4：将所提取的主成分因子代替原始指标，采用本文所定义的公式(3)加权主成分距离，为分类统计量进行聚类，并结合实际情况确定样本的所属类别.

2 仿真实验及结果分析

客观公正地评判模型的分类质量是困难而复杂的问题，目前没有评判所有聚类模型有效性的统一标准.在众多的评判标准中，比较客观的是将聚类模型的分类结果与预先已知的本来类属进行对比，以错分率为标准判断不同聚类模型的优劣.为验证拓展聚类模型的有效性，本文选用三个不同品种鸢尾花，将其花瓣长度、花瓣宽度、萼片长度、萼片宽度四个指标生成原始数据，下面说明原始指标间的信息高度重叠.按照累计贡献率≥85%的原则，提取了两个主成分因子，主成分因子的特征值、方差贡献率、和因子载荷矩阵见表1.

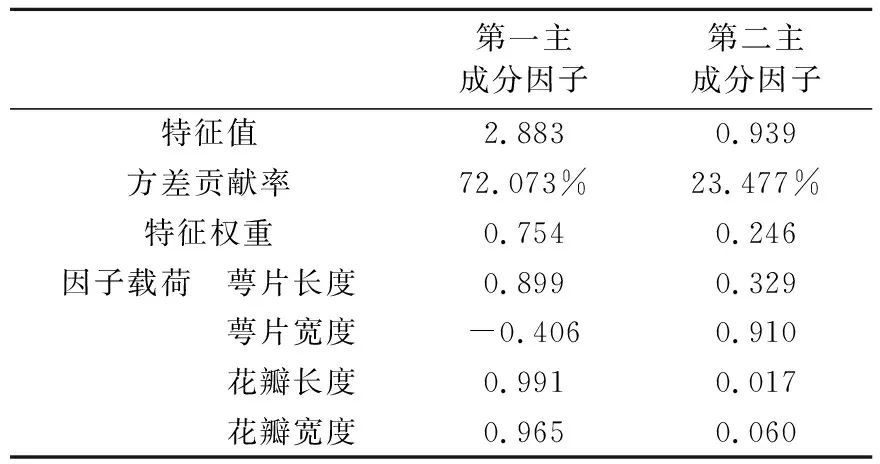
表1 主成分分析结果

表1结果显示，所提取的两个主成分因子的累计贡献率达到了95.55%，能够反映原指标变量的大量信息.由特征值知第一主成分所含信息量是第二主成分因子的3倍，说明两个主成分因子对分类重要性差异较大.因此忽略两个主成分因子对分类重要性的客观差异，而只是采用一般主成分聚类分析方法对两个主成分因子等权重地进行聚类，一方面无法显现出第一主成分因子对于提高分类质量的突出作用，另一方面还会过于放大第二主成分因子的作用，导致低效率的分类结果.而如果采用加权主成分聚类分析方法，先按特征权重对主成分因子赋权，再对赋权的主成分因子进行聚类，虽然考虑了不同主成分因子对分类重要性的客观差异，但其放大了第一主成分因子对分类的重要性，分类结果的精度亦难以保证.

本文分别用传统聚类方法、一般主成分聚类方法、加权主成分聚类方法和加权主成分距离聚类方法对标准化处理后的鸢尾花无量纲数据进行聚类分析.由于距离维数对分类结果有影响，本文分别测量并对比的在距离维数q=2，q=3，q=4情形下的各聚类的效果，如表2所示.

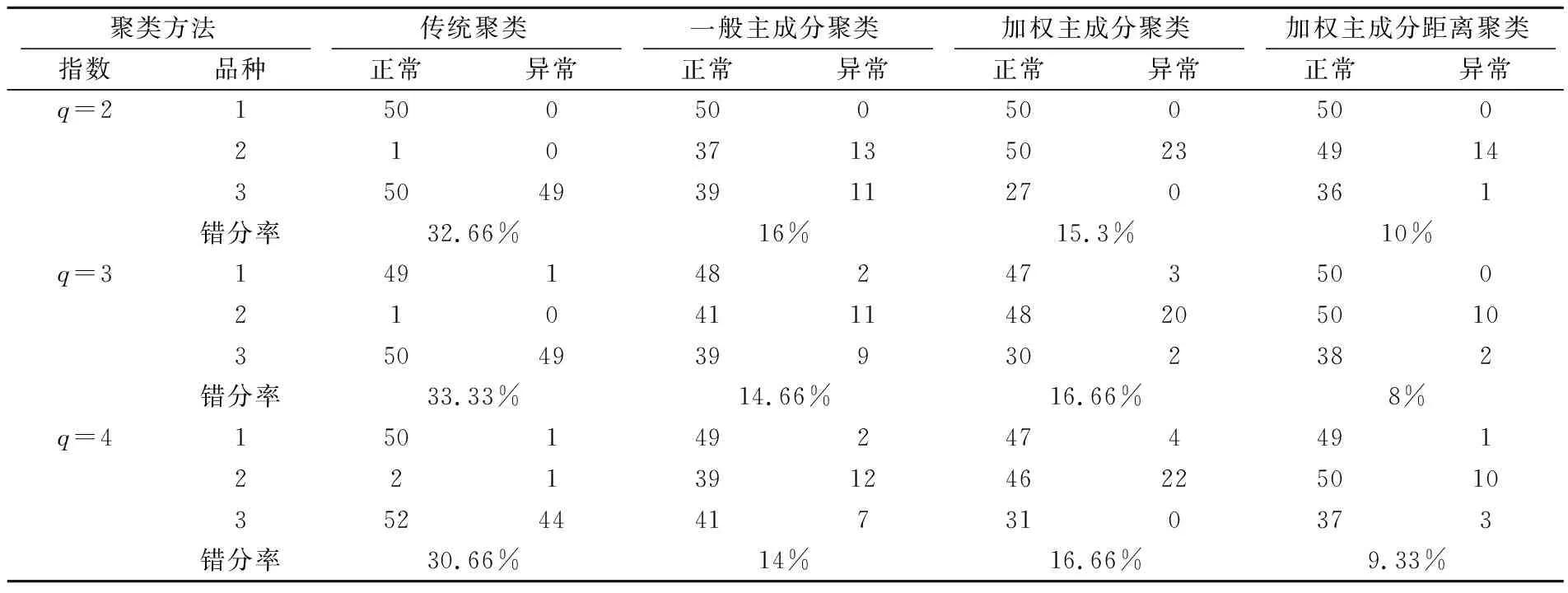
表2 不同聚类方法的分类效果

由表2可知，在q=2时，以错分率为标准，聚类的优劣次序为加权主成分距离聚类、加权主成分聚类、一般主成分聚类、传统聚类.在q=3和q=4时，以错分率为标准，聚类的优劣次序为加权主成分距离聚类、一般主成分聚类、加权主成分聚类、传统聚类.

根据分类结果来看，传统聚类的分类效果最差，一般主成分聚类和加权主成分聚类的效果也不理想.结合表1的计算结果，其原因是各指标之间存在较高的相关性，并且本文提取的两个主成分因子的信息含量分别为72.073%和23.477%.采用一般主成分聚类分析方法的时候减弱第一主成分的作用增强第二主成分的作用，因此导致分类效果不明显.采用加权主成分聚类分析方法的时放大了第一主成分的作用(特别是在q=3和q=4时)，因此导致结果失真.

3 结论与启示

通过以上的分析，在相同情况下，用不同的分析方法得到不同的分析结果，显然可以看出加权主成分距离聚类方法的错分率要远低于其他的几种方法，这为聚类方法提供了一种更为严谨的分类方案，显然这种聚类方案要优于其他的几种聚类方案，而维数对结果的影响并不是很大.

统计分析模型的层出不穷为学术研究提供了广阔的选择空间，但是如果对统计分析方法的理论基础、适用性前提以及存在的问题缺乏深入理解，可能陷入统计方法的研究误区.指标之间的高度相关性导致传统的聚类分析方法无法取得良好的分类效果，通过主成分分析的方法可以将多维数据降至低维，避免指标之间的高度相关性对聚类产生影响.理论研究和实验结果证明加权主成分距离聚类的优点，在各主成分分子信息含量相差不大的时候等同于一般主成分聚类，在第一主成分信息含量远远大于其他主成分信息含量的情况下，避免了采用加权主成分聚类过度放大了第一主成分作用的因素.但是在原始指标变量之间相关较弱不具备主成分聚类分析的条件时，加权主成分距离聚类可能会失效，此时采用传统聚类分析方法较好.