基于混合测距的二阶锥规划节点定位算法
2018-07-19孙莹莹
孙莹莹,张 飞
(1.国网河南省电力公司 驻马店供电公司,河南 驻马店 463000;2.黄淮学院 信息工程学院,河南 驻马店 463000)
0 引 言
受硬件条件和无线环境因素的制约,在WSNs中对传感节点的定位仍是一项挑战的工作[1-4]。至今,研究人员已提出多类定位算法[5,6],依据定位过程是否需要测距,现存的定位算法归属为基于测距或非测距。与非测距定位算法相比,基于测距定位算法的精度较高。在基于测距定位算法中,通常依据信号的相关参数获取距离,如到达时间(time of arrival,ToA)、到达角度(angle of arrival,AoA)[6,7]以及信号强度(received signal strength,RSS)。
此外,考虑了节点能量的局限性和定位精度,常引用协作混合定位算法[8]。文献[9]采用了线性最小二乘(least squares,LS)和优化估计的定位算法,而文献[10]采用了基于RSS差和AoA测量的LS和最大似然估计(ML)的定位算法。相应地,文献[11]通过权重LS求解基于RSS/AoA混合定位问题。
上述的这些算法均采用集中式方案求解混合测距定位问题。尽管集中式方案在大型网络具有较高的稳定性,但是具有足够计算机容量的集中处理器可能难以获取。因此,分布式方案更具有可操作性。
为此,提出分布式的基于RSS-AoA测距的二阶锥规划节点定位(RSS and AoA-based second-order cone programming target localization,R-S-SOCP)算法。R-S-SOCP算法充分利用RSS和AoA测距的优势,获取测量值,然后再利用最大似然(maximum likelihood,ML)估计获取未知节点位置,最后由SOCP将ML估计转换成SOCP的凸优问题。实验数据表明,提出R-S-SOCP算法能有效地降低定位误差。
1 定位模型
考虑一个大型传感网络,其由M个未知节点和N个锚节点构成。同时,引用S={s1,s2,…,sk,…,sM} 表示未知节点集和A={a1,a2,…,ai,…,aN} 表示锚节点集。
相应地,锚节点位置矢量表示为ai∈R3, 且∀i∈A, 而未知节点位置矢量表示为xk∈R3, 且∀k∈S。
当两节点在彼此通信范围R内,这两个节点间才能建立连接。为此,所有未知节点和锚节点链路以及未知节点与未知节点间链路分别定义为
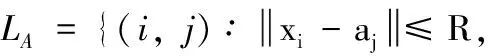
(1)
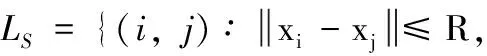
(2)
引用基于RSS和角度AoA测距算法,估计未知位置,测距模型如图1所示。
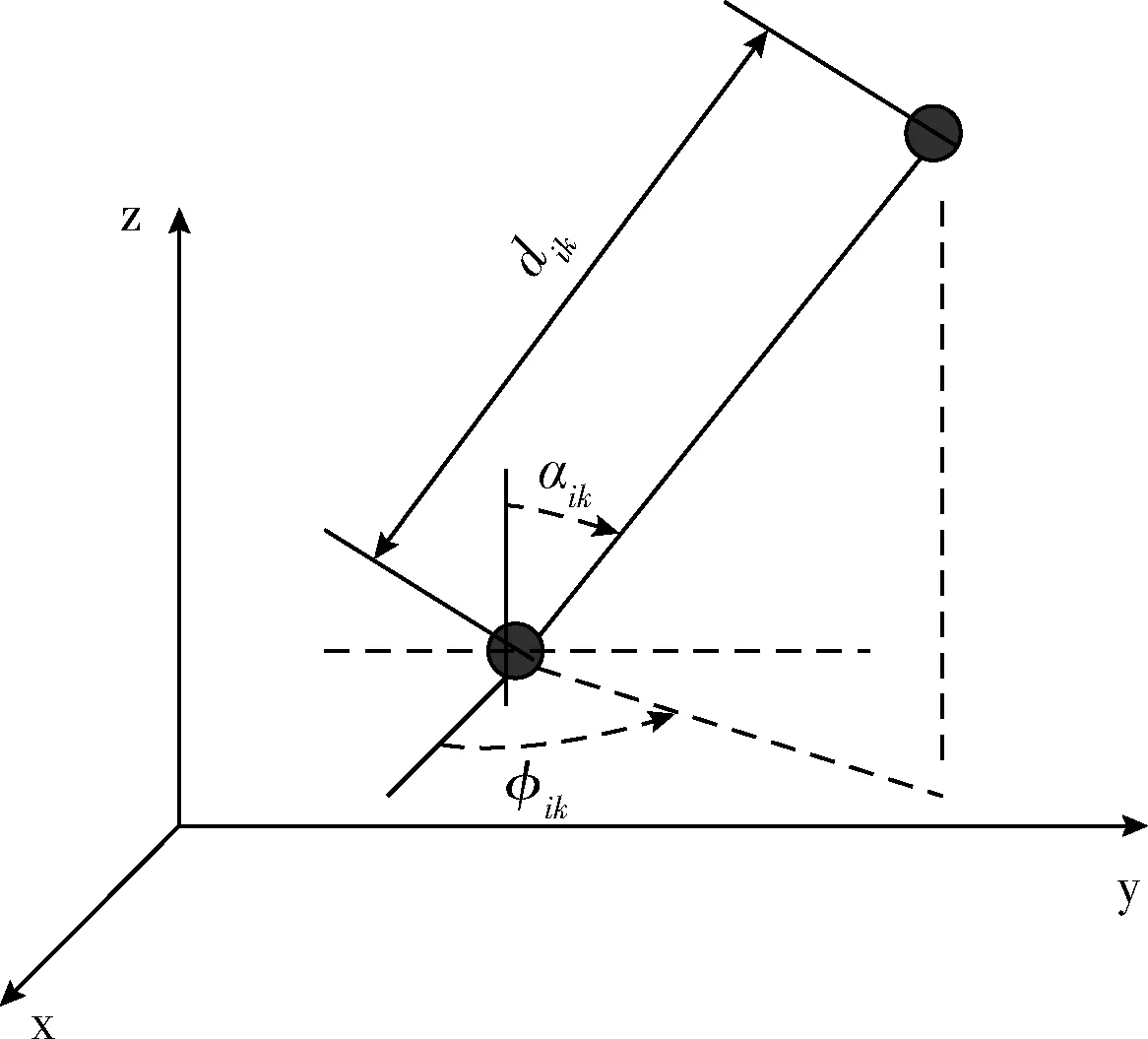
图1 定位模型
假定第k个未知位置的笛卡尔坐标为x=[xk,yk,zk]T, 而第i个锚节点的笛卡尔坐标为αi=[αix,αiy,αiz]T。 图1中的dik、φik和αik分别表示k个未知节点离第i个锚节点间距离、方位角和仰角。
由于RSS测距无需额外硬件设备[12],先利用RSS值进行测距。在无噪声条件下,两个节点i、j间的RSS值Pij(W),定义如式(1)所示[13]
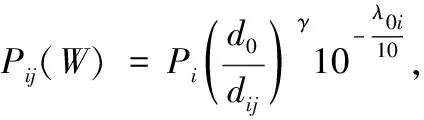
(3)
式中:Pi为第i个传感节点的发射功率,而λ0i表示第i个传感节点在参考距离为d0时的路径衰耗,且d0≤dij。其中dij表示两个节点i、j间的距离。
(4)
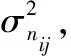
接下来,引用AoA测量。锚节点引用全向天线或天线阵列测量角度。因此,通过简单几何理论,引用文献[9]理论,可测量方位角
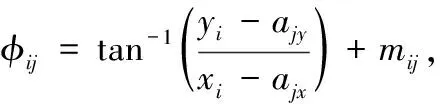
(5)
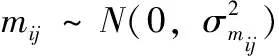

(6)
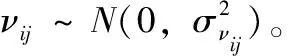
假定观察矢量θ=[LT,φT,αT], 且θ∈R3N, 其中L=[Lij]T、φ=[φij]T和α=[αij]T。 假定条件概率密度分布函数(probability density function,PDF)
(7)
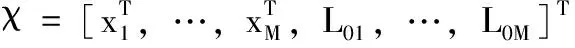
而函数f(χ)
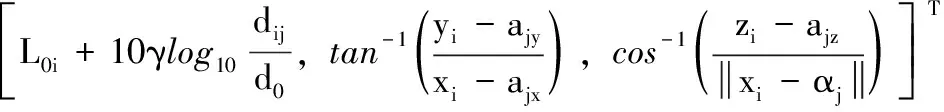
(8)
最后,利用最大似然估计算法估计未知矢量χ的值,可得[14]
(9)
注意到,最大似然估计是非凸优的,且无封闭的解。因此,需用近似求解法,进而获取闭合解,提高定位精度。
2 R-S-SOCP算法
R-S-SOCP定位算法主要包括测距和定位算法两部分。先利用RSS和AoA进行测量,然后利用最大似然估计建立式(9),再通过最小二乘估计未知位置,并作为局部ML的迭代初始值,最后,利用SOCP求解未知位置。R-S-SOCP 定位算法的总体模块如图2所示。

图2 R-S-SOCP定位算法的总体模块
2.1 局部ML估计
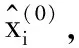
因此,利用局部最大似然估计,计算未知i在第t+1次迭代时位置估计值,如式(10)所示
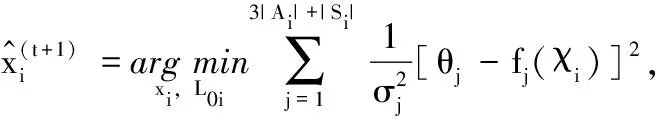
(10)
式中:Ai={j∶(i,j)∈A}、Si={k∶(i,k)∈S} 分别表示第i个未知节点的所有邻居的锚节点和所有邻居的未知节点。
而函数fj(χi)
(11)
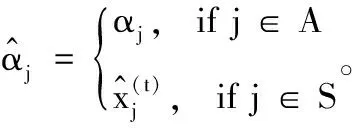
若噪声较小的环境下,并结合式(4)可得
(12)
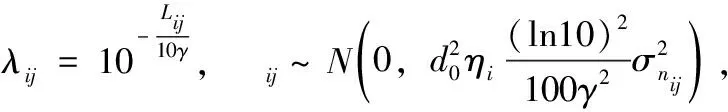
对式(8)两边进行平方,再丢掉二阶噪声变量,可得
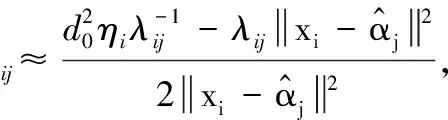
(13)
类似地,式(5)和式(6)可分别转换成
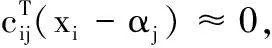
(14)
(15)
其中,cij=[-sinφij,cosφij,0]T, 且k=[0,0,1]T。
利用三角函数知识,并忽略二阶噪声变量,从式(15)可知
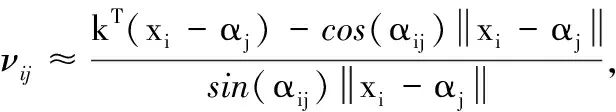
(16)
最后,基于LS准则,并利用式(13)、式(14)和式(16),可得

(17)
注意到式(17),式(17)的解是一个非凸、非封闭解。为此,利用SOCR算法转换成凸优解。
2.2 SOCR算法
引用epigraph变量e、ρ和q,利用这些变量转换式(17),进而将式(17)转换成SOCP问题,如式(18)所示
(18)
约束条件
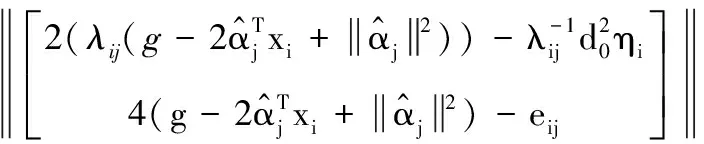
(19)
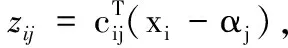
(20)
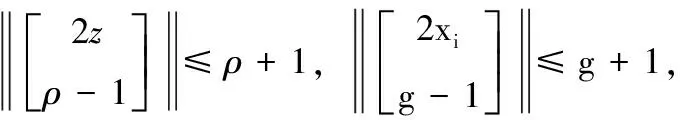
(21)
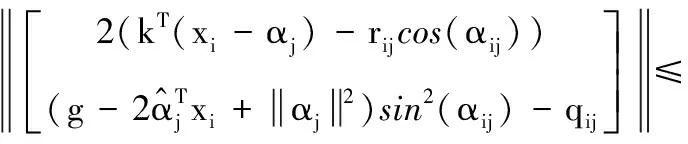
(22)
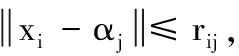
(23)
式(18)是典型的SOCP问题,可通过Matlab软件的工具箱CVX有效解决[14],基于SOCP的定位方案的流程如图3所示。
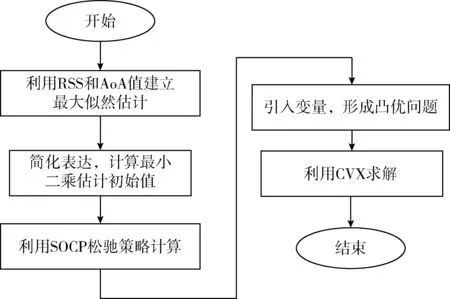
图3 R-S-SOCP算法的定位流程
3 性能分析
通过3.07 GHz的处理器、8GRAM的计算机,并结合MATLAB 2009a建立仿真平台,同时利用工具箱CVX计算SOCP问题。
本小节分析算法定位的准确性,选用定位均方误差RMSE作为性能指标,其定义如式(24)所示
(24)
假定仿真区域内有M个未知节点、N=9个锚节点,仿真区域为50 m×50 m。而参数路径衰落指数γ=3、参考距离d0=1 m。
(1)实验一
首先分析当M=6,R=6 m,方差σ=5 dB仿真场景。9个锚节点的位置分别为:(40,12)、(18,35)、(-5,39)、(-30,8)、(-13,44)、(0,-6)、(37,-23)、(30,20)。仿真结果如图4所示。
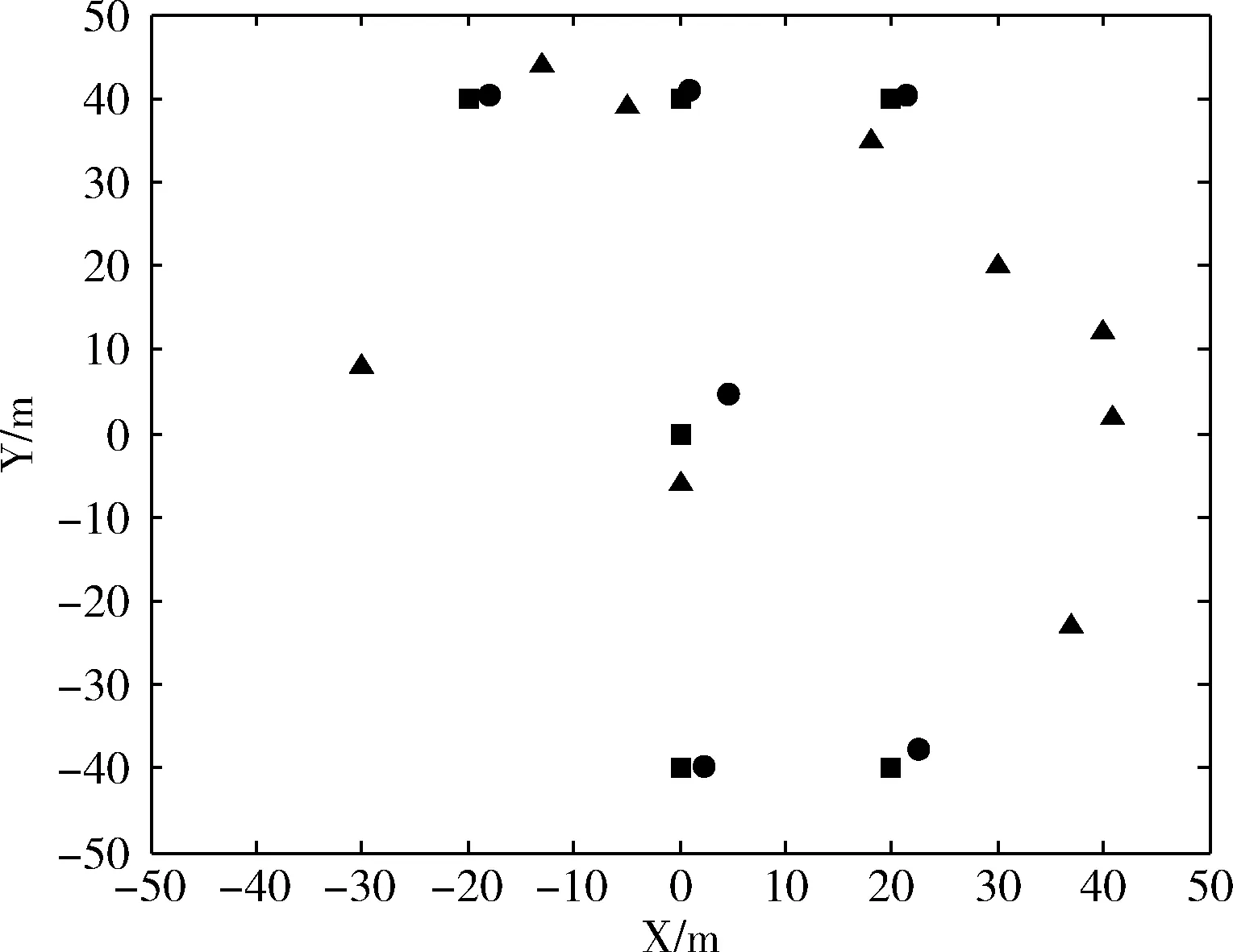
图4 R-S-SOCP算法估计6个未知节点的位置
图4描述了R-S-SOCP算法估计未知节点位置情况,其中“▲”代表锚节点,而“■”代表未知节点、“●”代表对未知节点的位置估计。从图4可知,提出的R-S-SOCP算法能够较准确地估计未知节点的位置。“●”均在“■”附近,甚至重叠。
(2)实验二
表1显示了各算法的复杂度。从表1可知,R-S-SOCP算法的复杂度高于SDPURSS和WANG算法,R-S-SOCP算法的复杂度为2·O(N3.5)、而SDPURSS、WANG算法的复杂度分别为O(N3.5)和O(N)。这说明R-S-SOCP算法是以一定的复杂度换取定位精度。
(3)实验三
最后,节点通信半径R对RMSE影响,实验数据如图6 所示,其中N=9、M=6。
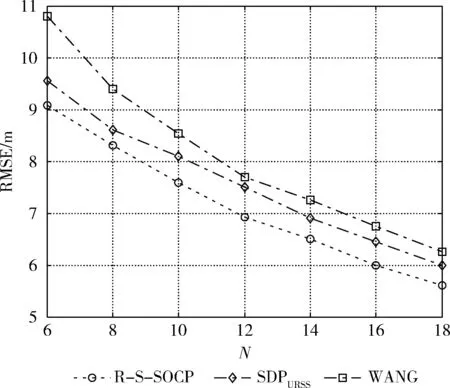
图5 定位均方误差RMSE随N的变化情况

算法算法具体描述复杂度WANGWANG估计[16]O(N)SDPURSSSDP估计[17]O(N3.5)R-S-SOCP本文提出的定位算法2·O(N3.5)
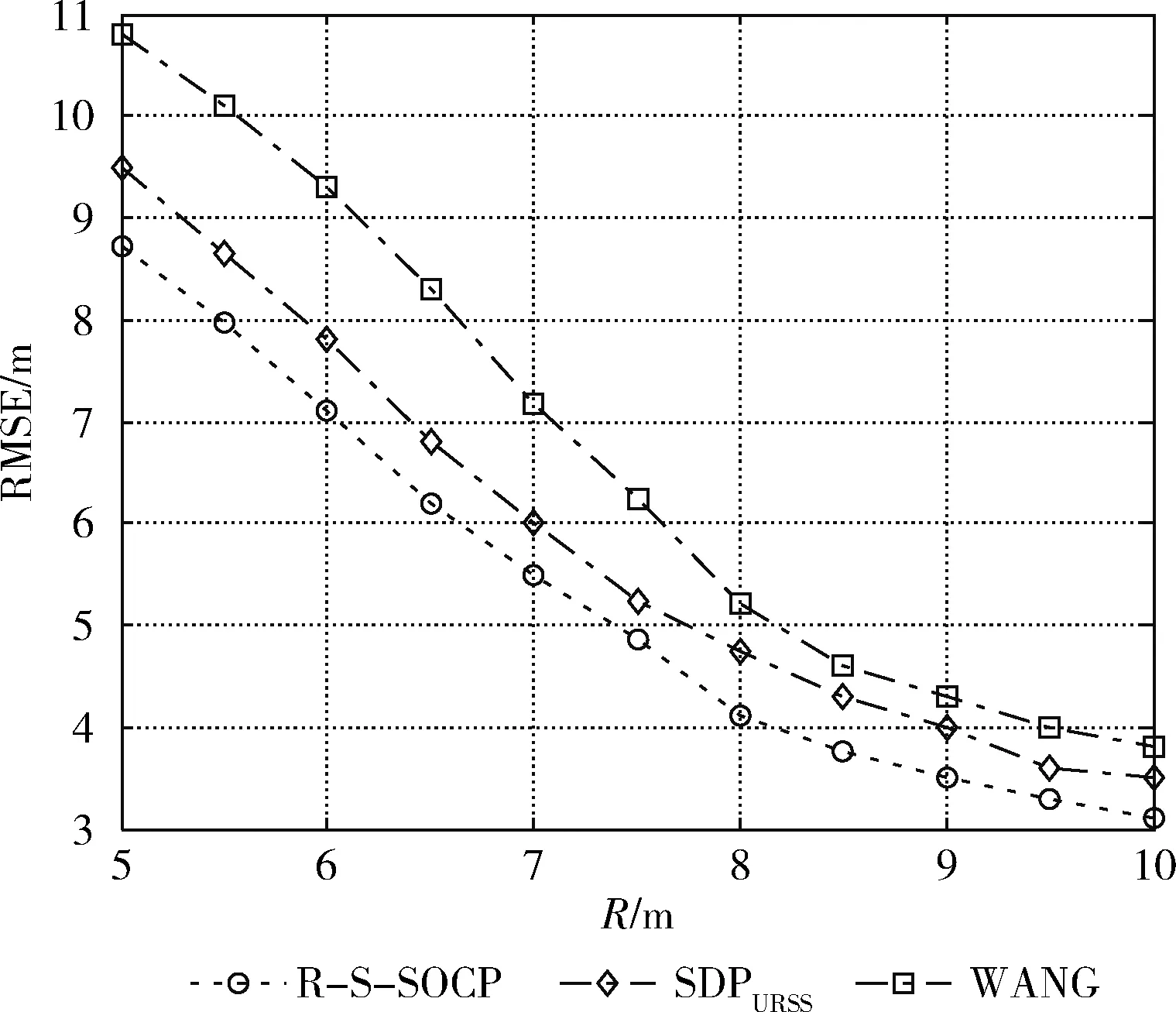
图6 RMSE随通信范围R的变化情况
从图6可知,RMSE随通信半径R的增加而下降,这主要是因为R的增加,提高了节点通信范围,使得未知节点能获取更多的测距信息,这有利于定位精度的提高。与WANG、SDPURSS相比,R-S-SOCP算法的RMSE分别下降了近1 m、0.5 m。
4 结束语
本文针对无线传感网络的节点定位问题,提出基于RSS和AoA的二阶锥规划的R-S-SOCP算法。R-S-SOCP算法通过结合RSS和AoA测量信号参数,再建立定位模型,然后利用SOCP建立定位SOCP定位优化问题,最后由CVX求解未知节点位置。通过引用RSS和AoA测量的优势,降低了测距误差。同时,建立SOCP模型,提高定位的精度。实验数据表明,提出的R-S-SOCP算法有效地降低定位误差。此外,通过表1可知,提出的R-S-SOCP算法提高算法的复杂度。在后期,在维持算法精度的同时,优化算法,降低算法的复杂度。
