典型零件形体的热变形模型及其有限元仿真
2018-07-19金少搏赵凤霞李纪峰
金少搏,赵凤霞,李纪峰
(郑州大学 机械工程学院,河南 郑州 450001)
1 引言
随着精密技术的精度不断提高,温度变化带来的影响愈来愈大,甚至成为制约精度的决定因素,并使传统的热变形误差理论失去作用[1]。近年来,文献[2-5]中对轴类、孔类零件在均匀温度场和非均匀温度场下的热变形规律进行了研究和探索。文献[6]中以有限元为工具,研究了稳态场下圆柱筒尺寸变化规律;文献[7]中基于ANSYS对主轴热变形进行了建模与预测分析;文献[8]中对模块化工具系统中非线性温度下的主轴热变形位移量进行了数学建模,并提出了补偿模型。但以上研究大都针对孔轴零件进行热变形研究,对球类、板类零件研究较少。基于弹性力学和热力学建立了典型零件形体的热变形数学模型,基于ANSYS有限元分析软件对典型零件形体的热形误差及其分布进行了仿真,并进行了实验验证,最后进行了实例应用分析。
2 典型零件形体的热变形模型
圆柱孔类、轴类、板类、球类零件是机械结构中的典型的基本零件形体。以上典型零件形体为例,建立零件的热变形数学模型。
2.1 圆柱轴类零件的热变形模型

图1 轴类零件示意图Fig.1 The Shaft Parts Diagram
假设实心圆柱的半径为R。弹性模量为E,泊松比为v,材料热膨胀系数为α。圆柱处于温度场T中,温度T对称于中心轴线,并与轴向坐标z无关。受温度变化的圆柱所产生的应变包括两部分,一部分是受热后材料的热膨胀引起的,另一部分是由应力引起的。
在圆柱上取微元进行分析,如图1所示。设σr、σθ、σz分别是径向、环向和轴向的应力分量,τθr、τθz、τrθ、τrz、τzθ、τzr为对应的剪应力。应力平衡方程为[9]:
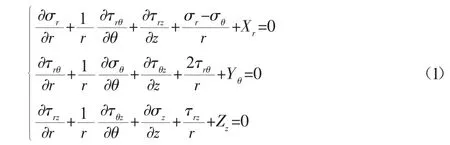
式中:Xr、Yθ、Zz—r、θ、z方向每单位体积的体力。
因为考虑到轴对称和沿轴向的均匀性,零件温度变化仅为r的函数,τθr、τθz、τrθ、τrz、τzθ、τzr都是零。一般地,物体的重力是唯一的体力,在不考虑零件自身重力和残余应力情况下,应力平衡方程可简化为:

设 εr,εθ,εz分别是圆柱径向、环向和轴向的实际应变,则由应力引起的应变为:

首先假设圆柱两端为自由端,温度变化引起的轴向位移w=0,则 εz=0。由式(3)可得:
σz=v(σr+σθ)-αET (4)
代入式(3)得:

设ur是圆柱受热后产生的径向位移量,则有:

将式(4)、式(5)代入式(2)得:
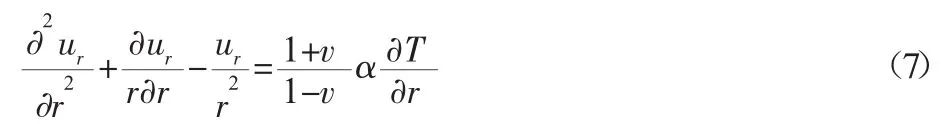
对式(7)进行积分得:
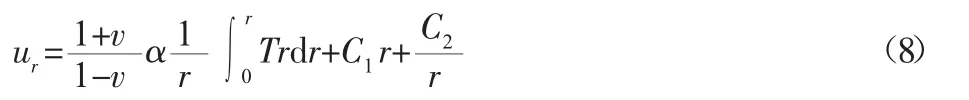
将式(8)代入方程(6),再将所得结果代入式(5),得到:

式中:C1、C2—积分表达式常系数,须由边界条件确定。
在r=0时,为使径向位移在圆心为0,由式(8)可知,C2必须为0。在圆柱边缘,当r=R时,假设曲面不受力,即σr=0,由式(9)可以求得其常系数
式(8)是假设轴向位移w=0得到的,实际中,温度的变化也会产生轴向位移,使w≠0。为使w=0,需要在圆柱两端施加满足按式(4)分布的轴向力,使总的轴向力为0,所施加的轴向力也将产生径向位移。因此,需要去掉由于轴向力影响而产生的径向位移,式(8)变为:

将 C1、C2、σz代入式(11),推得由于温度变化所产生的圆柱径向位移u′r为:

2.2 圆柱孔类零件的热变形模型
假设圆柱孔类零件的内径为R1,外径为R2,内表面温度为T2,外表面温度为 T1。
由边界条件知,在两个半径处σr=0,由式(9)可以求得C1、C2:

将C1、C2、σz代入式(10),得到圆柱孔零件由于温度变化所产生的径向位移为:

传统的零件热变形量计算公式为[10]:
Δd=d0αΔT(13)
很明显,式(13)中,由于温度变化引起的直径变形量只与孔的内径d0有关,与其他的几何尺寸没有关系,存在着很大的近似性,而式(12)则表明内径变化量与孔型零件的内径、外径和材料的特性等参数有一定的函数关系。
2.3 板类零件的热力学模型
假设矩形板类零件的长度为L,宽度为W,厚度为H,上表面温度为T2,下表面为T1。以该板的几何中心为原点,建立坐标系,如图2所示。
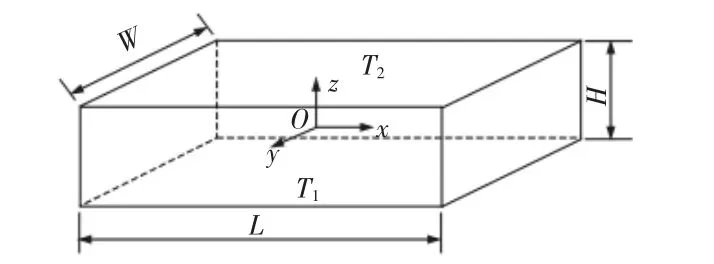
图2 板类零件的坐标系图Fig.2 The Coordinate System Diagram of the Plate Parts
根据零件的结构特征,可得高度z处的温度分布函数为:

2.4 球类零件的热力学模型
设实心球零件的半径为R,表面温度为T0,由于内外温度差比较小,可以看做等温体处理,即温度T=T0,其热变形方程为[12]:

对于空心球类零件,设内径为r1,外径为r2,内表面温度为T1,外表面温度为T0,根据空心球类零件的结构特征,可得出其相对于r的温度分布函数:

得到空心球零件的径向位移为:

注:限于篇幅,球类、板类零件热变形模型不再详细推导。
3 实验验证及应用分析
3.1 实验验证
现采用ANASYS软件对圆柱孔和轴类、板类零件进行热变形仿真,并利用中原精密仪器公司生产的Z600高精度检测仪器,对实际零件进行了热变形实验测量,实验装置,如图3所示。其检测精确度为1μm。

图3 实验装置图Fig.3 The Figures of Experiment Installing

图4 直径为50mm的圆柱轴在100℃的热变形云图Fig.4 The Hot Deformation Nephogram of Cylindrical Shaft with a Diameter 50mm at 100℃
该试验件材料均为45#钢,线膨胀系数α=12×10-6/℃,弹性模量 E 为 206GPa,泊松比 v=0.3,标准室温为 20°C,工作温度范围(30~100)°C,以 10°C 为间隔进行仿真,从而得到不同温度下圆柱孔和轴的热变形云图。典型零件的热变形云图,如图4~图6所示。分别记录不同温度下的最大变形量,结果如表1~表3所示。同时用上节所得到的热力学模型计算热变形量的理论值,如表1~表3所示。最后将实验测量实验数据也记录在表中。

图5 内径为50mm外径为100mm的圆筒在内表面温度为90℃的热变形云图Fig.5 The Hot Deformation Nephogram of the Hole with Inner Diameter 50mm and Outer Diameter 100mm,the Surface Temperature at 90℃

图6 长为50mm,宽为40mm,高为30mm的板在上表面温度100°C的热变形仿真图Fig.6 The Hot Deformation Nephogram of the Plate with Length 50mm,Witdth 40mm,Height 30mm at 100℃

表1 直径为50mm长度为100mm的轴零件在不同温度下的径向变形量(μm)Tab.1 The Radial Deformation of Shaft with a Diameter of 50mm,Length of 100mm at Different Temperature(μm)

表2 内径为50mm外径为70mm长度为150mm的孔零件在不同温度下的径向变形量(μm)Tab.2 The Radial Deformation Value of the Hole with a Inner Diameter 50mm,and Outer Diameter 70mm,and Length 150mm at Different Temperature(μm)
分析以上表中数据可知,测量值与理论值、仿真值非常接近,验证了模型的可靠性以及有限元仿真的正确性。但是理论值与实际测量值还是产生了(0.1~1)mm的偏差,经分析,主要存在于三点:首先是测量器具与温度计的自身误差,其次由于测量过程中工件温度降的过快,读取的值有稍微的滞后性,再者就是读取误差。限于篇幅,其他测量数据不再详述。对典型零件形体的热变形仿真提供了零件形体的变形分布状况,模型为设计者考虑热变形提供了参考。

表3 长为50mm,宽为40mm,高为30mm的板的板类零件在不同温度下的径向变形量(μm)Tab.3 The Radial Deformation Value of The Plate with Length 50mm,Witdth 40mm,Height 30mm at Different Temperature(μm)
3.2 热变形模型应用分析
随着温度的增加,零件的变形量增大。尤其是对于孔轴装配体,由以上实验数据可以看出,在温度较低时,孔与轴的变形量基本相同,因此在低温时孔和轴不会因温度变化影响其配合性质,但在温度较高时,孔与轴的变形量差异较大,且轴的变形量较大,因此在设计孔与轴的配合时,应考虑热变形的影响,将孔和轴的配合精度控制在一定范围内。
以铝制活塞与钢制缸体的装配体为例,配合公称尺寸为φ150mm,缸体外径为 φ180mm,要求工作间隙为(0.1~0.3)mm;缸体工作温度tH=110℃;活塞工作温度ts=180℃,线膨胀系数αs=24×10-6/℃,弹性模量 Es=70GPa,泊松比 v=0.26。
采用传统的热变形公式,由热变形引起的间隙变化量为:

采用所给的热变形公式,热变形所引起的间隙变化量为:

由式(11)和式(12)分别计算得到uH=0.056mm和us=0.288mm,得到Δ=-0.464mm。
其装配热变形分布,如图7所示。可见热变形误差将使得以孔轴配合为典型装配的工作间隙减小。因此,在设计之初就将温度变化对零件的影响考虑进去,设计时在配合偏差上叠加一个补偿量,来抵消零件因温度变化而带来的热变形量,以此为依据可对配合结构进行最佳热配合设计。

图7 活塞与缸体配合的热变形云图Fig.7 The Hot Deformation Cloud Figure of the Fit of Piston and Cylinder Block
4 结论
热应力所产生的变形量在总热变形量中占有一定的比例,在精度要求高的情况下更不能被忽视。(1)基于弹性力学和热力学建立了圆柱轴和孔类、板类、球类零件形体受温度变化时的热变形误差模型,该模型考虑了热应力对热变形的影响,相对于传统计算方法更加合理。(2)采用ANASYS有限元分析软件对典型零件形体的热变形误差及其分布进行了仿真,并以实验验证了仿真及热变形模型的正确性。得到了孔和轴随温度变化的热变形规律,为合理进行零件的公差与配合设计提供了理论依据。
