四足机器人静步态连续行走策略
2018-07-19刘明敏
刘明敏 ,徐 方
(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2.中国科学院大学,北京 100049;3.沈阳新松机器人自动化股份有限公司,辽宁 沈阳 110168)
1 引言
经过多年的研究,移动机器人已经广泛应用工业、农业,而足式机器人作为移动机器人的重要组成部分,它具有非连续地面支撑的运动特点,能够跨越崎岖复杂的地形,具备在非结构化环境中的应用潜力,因此近年来成为研究的热点。四足机器人的步态分为静步态和动步态[1]。静步态强调稳定,动步态注重运动的快速性、灵活性。文献[2]提出浮动基座逆动力学控制和预测力控制策略,并实现了little dog在复杂路面的静步态稳定行走。文献[3]通过对足端轨迹进行规划,实现了液压四足机器人在平地上的对角小跑步态,文献[4]提出了一种零冲击足端轨迹规划算法,文献[5]提出了一种基于参数化矩阵的运动规划方法,实现四足机器人在平面上的转向与斜向运动。文献[6]利用Bezier曲线设计了四足机器人足尖运动轨迹,并实现了高负载四足机器人水平面对角小跑。
以实现四足机器人在平面上稳定、连续行走为目标,提出一种基于walk步态零冲击足端轨迹规划方法。首先运用DH算法推导出单腿的运动学方程。然后采用直线规划支撑腿时足端的运动轨迹,五次曲线规划摆动腿在水平方向上的足端轨迹,摆线规划摆动腿在竖直方向上的足端轨迹。以静态稳定裕度为评价指标,评价了四足机器人在连续行走过程中的稳定性。最后进行仿真实验,验证算法正确性。
2 四足机器人运动学模型建立

图1 左前腿坐标系建立示意图Fig.1 Illustration of the Left Front Leg Coordinate System
一般足式机器人的每条腿有3个自由度(其中1个外摆自由度、2个横滚自由度)即可满足四足机器人运动性能的要求。根据关节配置结构,运用DH算法建立其左前腿运动学模型,其坐标系建立,如图 1 所示。图中:L1,L2,L3—侧摆,大腿,小腿的长度;a,b—前后,左右髋关节距离的一半。其DH参数,如表1所示。表中:αi-1,ɑi-1,di,φi,—连杆长度,连杆扭角,关节距离,关节转角。

表1 DH参数Tab.1 DH Parameters
将DH参数带入齐次变换矩阵(1)
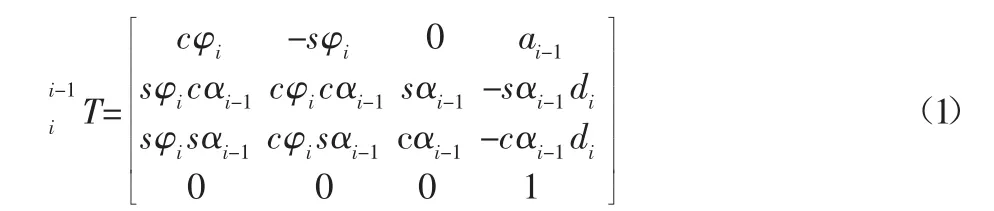
得到各关节之间的变换矩阵:
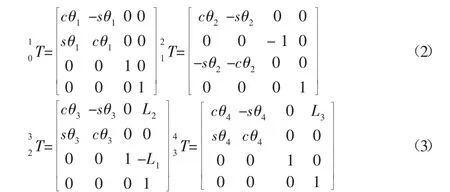
最后将各个关节的变换矩阵依次右乘便得到机器人足端位姿矩阵

因此右前腿的足端坐标为:

式中:c1,s1,c23,s23—cosθ1,sinθ1,cos(θ2+θ3),sin(θ2+θ3)。
对正运动学方程反解可求出逆运动学方程,即给出机器人足端末端的位置就可求出各个关节的角度。
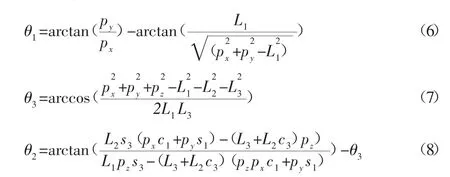
这里只推导了一条腿的运动学,同理替换髋关节坐标系可求出其他三条腿的运动学。
3 轨迹规划
3.1 步态规划
四足机器人的步态分为静步态与动步态。静步态任意时刻至少有三条腿作支撑。当任意时刻支撑腿少于三条时为动步态。静步态行走时稳定性较好,但是速度较慢。仅考虑迈腿次序的组合,静步态的共计24种[7]。为了保证四足机器人在运动过程中保持平稳,机器人的重心的投影要求落在支撑点组成的多边形内。因此只有四足机器人的迈腿顺序为左前腿-右后腿-右前腿-左后腿,如图2所示。四足机器人可以在平面上稳定连续的行走。

图2 直线行走步态运动策略Fig.2 The Linear Walk Gait Locomotion Strategy

图3 直线行走时序图Fig.3 The Sequence Diagram of LinearWalk
3.2 零冲击足端轨迹规划
为了使四足机器人连续、稳定的运动,基于所求的运动学方程及步态规划,给出零冲击足端轨迹规划算法。在运动过程中,每条腿会相对躯干摆动腿与支持腿之间进行周期性摆动。为了达到期望的运动状态足端轨迹要符合以下条件:(1)位置、速度、加速度连续;(2)摆动腿在起脚与落脚的瞬间无冲击,实现软着陆;(3)在运动的过程中躯干匀速前进;
文献[4]对文献[9]所提出的摆线规划方法进行修正,提出一种零冲击的足端轨迹规划改进算法,避免了行走过程中足端的拖地、滑动和接触冲击等问题。其轨迹方程如式(10)所示:

竖直抬腿方向采用式(10)所规划的轨迹,在水平前进方向采用直线与五次曲线混合规划运动轨迹。其轨迹方程,如式(11)所示。

式中:H—抬腿高度;T—步态周期;L—迈步幅度。
单位化H,T,L后,前进方向轨迹方程的位置,速度,加速度曲线,如图4所示。由图像可知,在前进方向的轨迹不仅保证位置、速度连续,还保证加速度连续。

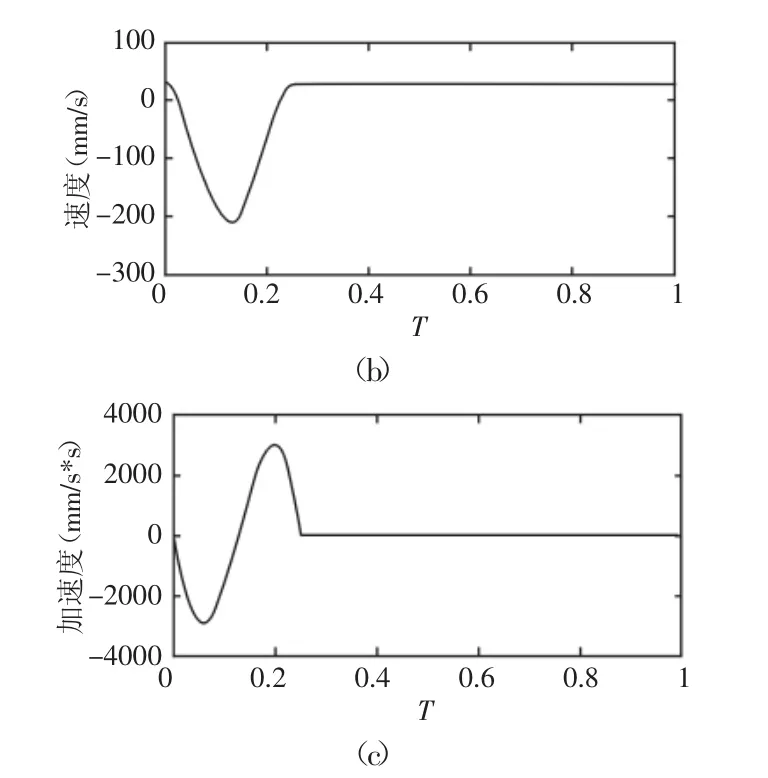
图4 轨迹方程曲线Fig.4 Trajectory Curve
3.3 稳定性分析
四足机器人的静态稳定性评价标准有很多,静态稳定裕度这个概念由McGhee和Frank提出[8]。对于四足机器人,静态稳定裕度等于机器人质心距离支撑三角形边界的最短距离,当质心位于三角形内部,取值为正;质心落在三角形外部,则取值为负;稳定裕度的值越大则机器人越稳定。根据轨迹规划方法,四足机器人一个运动周期内的稳定裕度曲线,如图5所示。

图5 一个运动周期内的稳定裕度曲线Fig.5 Stability Margin Curve of a Cycle
4 仿真验证
为验证算法的正确性,针对四足机器人walk步态连续直线行走的足端轨迹算法进行了仿真验证。仿真中机器人的各项物理参数,如表2所示。

表2 物理参数Tab.2 Physical Parameter
根据所规划的足端轨迹,运用逆运动学反解出各个关节的角度来驱动各个关节,实现轨迹跟随。其一个步态周期内的仿真截图,如图6所示。仿真结果证明机器人可以在水平面上稳定,连续的行走。在运动过程中无打滑,足端拖地,侧翻现象的发生。四足机器人在直线行走时大腿关节与小腿关节的所需的驱动力矩曲线,如图7所示。曲线表明在运动过程中,大腿关节与小腿关节所需的力矩变化平缓,足端与地面之间未产生较大的冲击。另一方面,力矩曲线也为四足物理样机的电机选型提供依据。

图6 仿真截图Fig.6 Snapshots of the Circular Walking Simulation
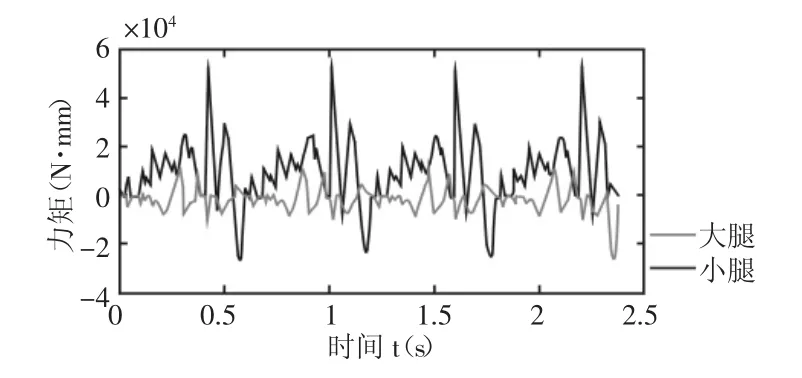
图7 大腿与小腿关节力矩图Fig.7 The Torque of Hip and Crus
5 结论
针对四足机器人在行走过程中出现冲击、打滑、侧翻等问题,提出一种了基于walk步态的零冲击足端轨迹算法。通过直线规划支撑腿时足端的运动轨迹;五次曲线规划摆动腿在水平方向上的足端轨迹;摆线规划摆动腿在竖直方向上的足端轨迹。以稳定裕度为指标评价了四足机器人在行走过程中的稳定性。最后仿真表明四足机器人可以在水平面上的稳定、连续行走,验证了算法的正确性。
