填充不同材料条件下管材三维自由弯曲变形行为研究
2018-07-19程旋魏文斌熊昊王成余耀晖万柏方王林涛陶杰
程旋,魏文斌,熊昊,王成,余耀晖,万柏方,王林涛,陶杰
(1. 南京航空航天大学 材料科学与技术学院,南京 210016;2. 江苏省核能装备材料工程实验室,南京 210016;3. 江苏图南合金股份有限公司,江苏 丹阳 212352)
三维自由弯曲技术作为金属塑性成形领域近年来一项先进技术创新,可实现管材、型材、线材精确无模连续弯曲成形,在汽车、航空航天、舰船等领域有广泛应用,对传统金属构件弯曲成形技术形成了巨大挑战,近年来受到越来越多的关注[1—3]。1989年,Murata等[4—5]首次提出自由弯曲技术,在不改变模具或重新夹紧的情况下,精确弯曲不同半径的复杂空心管和型材,并介绍了弯曲过程中弯矩的计算方法。Gantner等[6—7]建立了有限元分析(FEA)模型,对上述弯曲工艺进行了数值模拟,并通过弯曲试验进行了验证,另外,基于运动学和数学仿真结果,建立了理论模型,研究弯曲模的控制参数。随着相关技术研究的发展,不同类型的自由弯曲构型及运动学理论被不断完善[8—10],同时也被日本、德国等多家企业相继推出商用的自由弯曲成形系统。
三维自由弯曲技术作为一种无模成形技术,在管材弯曲过程中难以保持稳定并且产生回弹,对成形质量及成形精度有很大影响。当前常采用的办法是在管材内加入填充材料,在内部起到支撑作用,抑制管壁厚度的变化和回弹,并且提高成形性能[11]。目前用于管材弯曲的填充物,主要有固体填充物和柔性填充物。常用的固体填充物包括沙子、低熔点合金、钢球等,柔性填充物主要指水、橡胶、聚氨酯棒等,柔性填充物填充方便,可以通过改变压力而随意调整传递和存储能量的大小。近年来,国内外众多学者们通过实验或数值方法研究了填充材料对管材弯曲成形极限和成形性的影响。Langenbrunneri等[12]向管材中填充沙子,通过研究发现,在弯曲过程中,填充的沙子改变了能量平衡,内部支撑力做功抵消了造成内侧管壁失稳起皱的能量,因此可以抑制管材弯曲中的失稳起皱现象;Sedighi等[13]把低熔点合金和不同类型的橡胶作为填充物,研究不同填充物对薄壁管弯曲过程中出现的起皱、截面变形等缺陷的影响;石松朝[14]分析了固体颗粒的传压特性和管材弯曲成形的受力状态,研究了管材截面上的环向壁厚分布和内压力对壁厚减薄率的影响,并对管材固体颗粒填充绕弯成形中的失稳起皱现象从几何角度进行了描述,开发出以钢球为填充介质的管材固体颗粒填充绕弯成形装置,对实际生产有一定的指导意义;李海平等[15]研究发现,采用芯模可有效减小双脊矩形管绕弯成形过程中的截面畸变,并提高弯曲管件的成形精度;在脊槽部位填充材料的方法能够有效抑制双脊矩形管绕弯成形过程中的截面变形,但弯曲结束后刚性模具和填充材料的卸载对管坯截面变形存在一定影响。基于ABAQUS有限元平台,张曙光等[16]建立了脊槽填充材料的双脊矩形管 H型绕弯成形和卸载回弹过程有限元模型,并基于该模型,研究获得了双脊矩形管绕弯和卸载回弹前后截面各部位变形的变化规律;刘春梅等[17]基于ABAQUS有限元平台建立了双脊矩形管E弯成形三维有限元模型,研究了内外侧模具约束条件对双脊矩形管E弯截面变形的影响规律。
目前大多数学者主要研究的是芯棒、低熔点合金及固体颗粒等填充物的影响,对于聚氨酯棒等柔性填充物研究较少,且没有建立相关力学模型,分析比较固体填充物以及柔性填充物对成形质量的不同影响机理。文中通过向铜管填充钢球以及聚氨酯棒,分析研究了不同填充材料对于成形性能的影响机理,并将有限元模拟和实验相结合,验证了该理论模型的准确性。
1 不同填充条件下管材弯曲理论分析
1.1 材料模型的建立
根据塑性成形理论,在管材弯曲过程中,管材内侧受到压应力,使管材内侧壁厚增加;而管材外侧则受到拉应力,使管材外侧壁厚减薄。在三维自由弯曲过程中,由于轴向推力的存在,使管材壁厚变薄受到抑制。为保证模拟结果更接近实验,选择幂强化模型。该模型是一条光滑连续的加载曲线,没有明显的线性弹性阶段,适用于大多数金属和管材,其计算公式见式(1)。

式中:K为塑性系数;n为硬化系数
应力应变分析见图1,其中r0和r1分别是管材外径和内径,ρ是应变中性层处的半径,r是任一点处的半径。
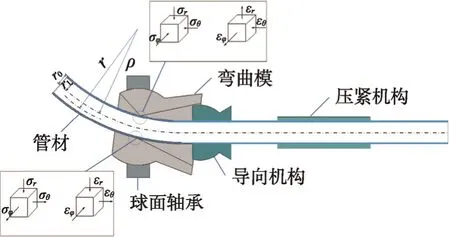
图1 管材弯曲应力应变分析Fig.1 Analysis on bending stress and strain of tube
管材弯曲切向应力σθ计算公式为:

在弯曲过程中,通常假定弯管的截面在垂直于弯曲平面的方向上不发生变化,且管材处于平面应变状态,则根据式(1),可以计算得到平面应变状态下的径向压力σρ和周向压力σφ,见式(3)和式(4),当rρ>时正号,当rρ<时,取负号。
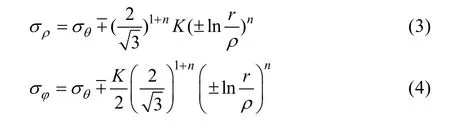
1.2 U-R关系的推导
在三维自由弯曲过程中,管材首先经历一个直线段,然后随着轴承向上运动逐渐弯曲,直至向上运动距离为U,U-R关系决定了管材弯曲成形精度,U-R关系推导如下。

图2 沿y轴方向位移Fig.2 Displacement along direction y
沿y轴方向位移见图2,在弯曲过程中,轴承沿y轴方向偏心距可以分解为:

式中:D1为管材在直线段运动时沿y轴的位移;D2为管材在弯曲段运动时沿y轴的位移。在直线段,管材前进距离L1等于管材在该段时间内的弧段长度。

式中:R为弯曲半径;φ是弯曲角。
设弯曲模中心与导轨前端的距离为A,由几何关系,可以得到:
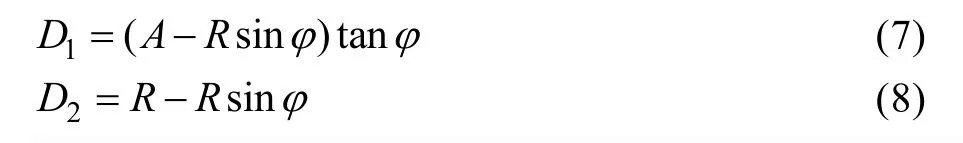
为方便控制,将z轴管材送进速度设为匀速,即:

联立式(5)—(9),可得U-R关系为:

1.3 填充不同材料的管材受力分析
当在管材中不填充材料时,管材受到弯曲模所施加的与管材轴线垂直的压力PU,以及轴向推力PL,受力分析见图3。

图3 无填充物时管材受力分析Fig.3 Force analysis of tube filled with nothing
则在水平方向:

竖直方向:

弯矩为:

当在管材内部填充钢球时,不但受到PU和轴向推力PL,还受到填充材料施加的垂直于内管壁的压力FN,应力分析见图4。其中θ为弯曲模与垂直方向的夹角,r2是所填充的钢球半径。

图4 填充钢球时管材受力分析Fig.4 Force analysis of tube filled with steel balls
则在水平方向:

在竖直方向:

弯曲时的弯矩为:

当选择聚氨酯棒(PU棒)作为填充物时,由于PU棒弹性高,易变形,因此在进行受力分析时,只考虑摩擦力Ff的影响,受力分析见图6。其中,Φ为弯曲模与水平方向夹角,Ff为PU棒与管材内壁直接的摩擦力,r3为PU棒的半径。

图5 填充PU棒时管材受力分析Fig.5 Force analysis of tube filled with PU rubber
则在水平方向:

在竖直方向:

弯曲时的弯矩为:

2 三维自由弯曲有限元模拟
为了研究不同材料填充管的三维自由弯曲过程,选用ABAQUS软件对其成形过程进行了数值模拟。所用的有限元模型包括球面轴承、弯曲模、导向机构、压紧机构、管材以及不同的填充材料6个部分,如图6所示。管材和弯曲模(被动运动,不设置为刚体),网格划分为C3D8R类型,填充材料被定义为可变形体,其他部件均定义为刚体,网格类型为R3D4。将相互作用设置为一般接触,管材与模具切向全局摩擦因数设置为0.02,并将分析步骤调整为动态显式。载荷设置中压紧机构和导向机构设置为完全固定,并在管材末端设置沿x轴方向的指定运动速度,轴承设置沿y轴方向的运动速度,填充材料不施加载荷。
使用铜管对不同填充材料的自由弯曲过程进行了研究,弯曲角设置为120°,弯曲半径设置为78 mm,铜管外径为15 mm,壁厚为1 mm,铜管长度为500 mm,弯曲模中心与导轨前端之间的距离为30 mm,偏心距为 4.5 mm,填充材料包括固体填充物 SS304钢珠以及柔性填充物PU棒,其相关参数见表1。

图6 自由弯曲有限元模型Fig.6 The FE modeling of tube free bending
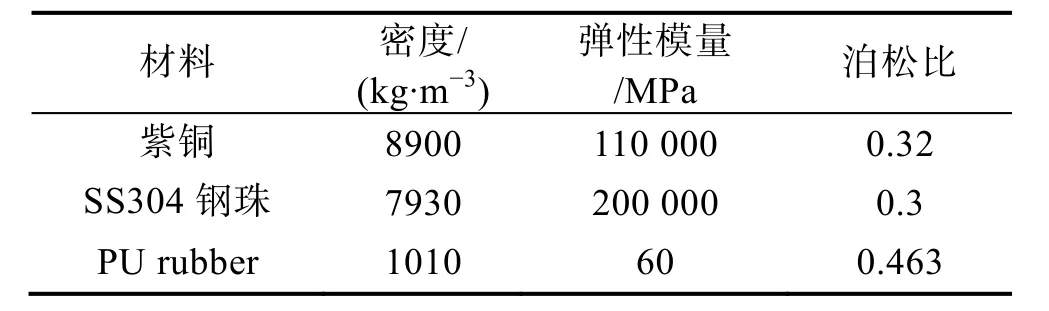
表1 材料参数Tab.1 Parameters of materials
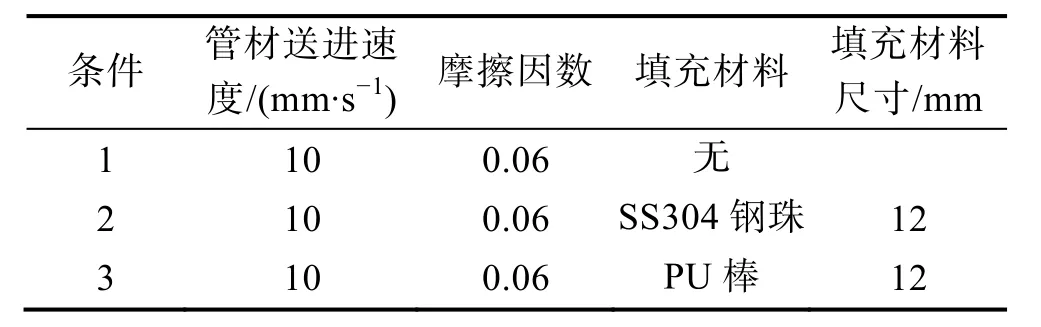
表2 不同条件下的模拟参数Tab.2 Parameters for simulation under different conditions
基于上述参数,在不同条件下的仿真结果见图7。

图7 不同条件下的仿真结果(MPa)Fig.7 Simulation results under different conditions
3 实验及分析
基于上优化工艺参数,在自主研制的三维自由弯曲成形设备上进行了实际的弯曲实验,见图8。

图8 三维自由弯曲实验Fig.8 Experiments of three dimensional free bending
填充不同材料时铜管外侧壁厚的分布规律见图9,可以看出,在不同条件下的成形过程中,壁厚变化规律相似,当弯曲角度分别为 20°和 90°时,由于弯曲模的运动,因此管材壁厚变化较大,外侧壁厚减薄较严重。当不填充任何填充物时,最大壁厚减薄率为 6.2%,当填充固体填充物时,外侧壁厚减薄受到抑制,最大壁厚减薄率降低至 5.8%,而当填充柔性填充物时,最大壁厚减薄率增加至6.6%。

图9 外侧壁厚分布Fig.9 Distribution of outer wall thickness
填充不同材料时铜管内侧壁厚的分布规律见图10,可以看出,填充固体填充物时,可以提高成形质量,而当填充柔性填充物时,反而降低管材成形质量。在不同条件下的成形过程中,壁厚变化趋势相似,当弯曲角度分别为 20°和 90°时,由于弯曲模开始运动或者回到起始位置,受到较大压力,因此管材壁厚变化较大,内侧壁厚增加较大;当填充SS304钢珠时,管材壁厚受到抑制,最大增厚率为18.8%,最小壁厚增厚率为17.4%,而当填充PU棒时,最大增厚率变化为20%,最小壁厚增厚率为18.6%。
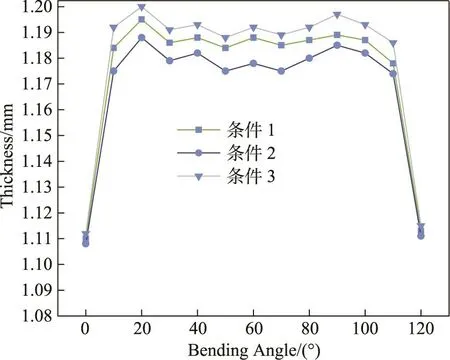
图10 内侧壁厚分布Fig.10 Distribution of inner wall thickness
填充材料对管材的截面椭圆率有很大影响,为研究不同填充材料对椭圆率影响程度,定义椭圆度为η,计算公式为:
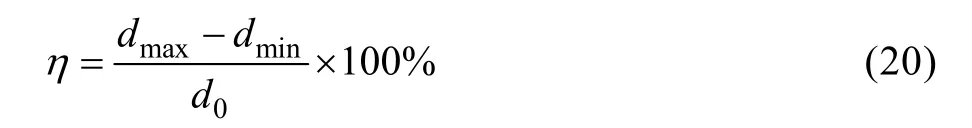
式中:dmax和dmin分别为管材最大和最小外径;d0为管材原始直径。
不同条件下的最大和最小管道半径和椭圆度见表3,可以观察到,无论填充材料是什么,椭圆度都在减小。当填充材料为SS304钢珠时,在条件2下,最小椭圆度可达2.6%。
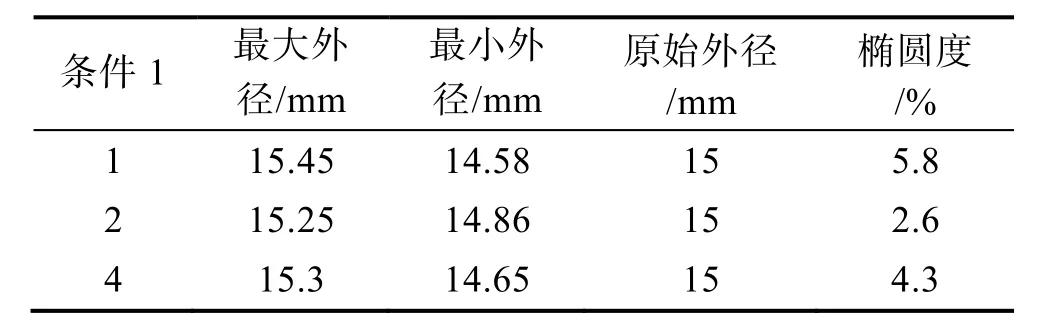
表3 不同条件下的外径及椭圆度Tab.3 External diameter and ellipticity under different conditions
4 结论
1) 将三维自由弯曲技术与填充成形技术相结合,可以有效提高管材成形性能,选择固体填充物 SS304钢珠作为填充物的性能要好于柔性填充物PU棒。
2) 与柔性填充物相比,填充固体填充物对于提高管材成形质量具有更好的效果,但当填充 SS304钢珠时,管材内部会产生凹痕,管材内表面质量变差。
3) 无论是固体填充物还是柔性填充物,均能降低椭圆度,当填充 SS304钢珠时椭圆度可以降低至2.6%。
