Al/Cu双金属管内旋压增量成形有限元数值模拟与分析
2018-07-19余耀晖王成程旋魏文斌熊昊陶杰
余耀晖,王成,程旋,魏文斌,熊昊,陶杰
(1. 南京航空航天大学 材料科学与技术学院,南京 210016;2. 江苏省核能装备材料工程实验室,南京 210016)
随着现代技术的发展,需要一些具有特殊能力和特性的管道材料,如具备耐腐蚀、重量轻、机械强度高等特性,单一的金属管无法满足这些需求,因此开发出了双金属复合管。双金属复合管是由两种不同的金属管材构成,管层之间通过各种变形和连接技术紧密结合,受外力作用时,基管与衬管同时变形且界面不分离。双金属复合管同时兼具两种基材的特性,充分发挥内管和外管的性能,不仅具有较高的强度和刚性,还具有优良的防腐蚀、重量轻、机械强度高等性能,而且降低了生产成本,广泛应用于油田、化工、电力等工业领域[1—4]。
目前对于双金属复合管的研究,潘毓滨[5]通过对Al/Al复合管和Cu/Al双金属复合管进行数值模拟和强力旋压实验相结合的方法,得出在强力旋压过程中,外层金属比内层金属所受到的等效应力大。S.Berski[6]等对双金属棒的挤压过程进行了分析,研究了模具形状和挤出比对该过程中电荷收率的影响。王悦[7]通过对Al/Al复合管和Cu/Al双金属复合管进行界面热阻实验、有限元模拟与旋压实验相结合的方法,对双金属管复合旋压的界面热阻效应、温度场分布以及成形工艺进行了研究;陆晓峰[8]等研究 20碳钢作基管、316L不锈钢作内衬管的双金属复合管的拉拔成形过程,分析稳定拉拔阶段成形区内轴向、径向和环向应力的分布,探讨拉拔力和内外管间残余接触压力的分布规律;Yuan HU[9]等通过液固复合铸造工艺制备 Al/Cu双金属材料,研究不同工艺参数下Al/Cu接头的显微组织、力学性能和导电性能;Ali Tajyar[10]等研究轧制工艺对Al/Cu双金属管的结合强度和机械性能的影响,得出随着各个阶段辊缝减小的增加,硬度增加,而剪切强度下降,然而,两种材料对硬度增加的影响并不相同;伊蒙生[11]对双金属复合管旋压成形过程进行数值模拟研究,将旋压过程分为起旋、稳旋和旋出模具3个阶段,分析了稳旋阶段的轴向、径向和周向的应力分布;徐文斌[12]等基于弹塑性力学理论,阐述了双金属复合管旋压成形过程的力学原理,并获得旋压过程中内外管残余接触压力最大时的最优径向应力、压头直径以及进给率。程可[13]等分析了衬管和基管径向、环向、轴向应力及其间的残余接触应力的分布;利用控制变量法研究旋压工艺参数对复合管残余接触应力的影响。上述学者通过旋压、挤压、拉拔、铸造、轧制等不同的加工方式对双金属管的成形做了研究,对成形过程中双金属管的应力应变状态、力学性能以及对成形后双金属管的结合强度、机械性能、显微组织等进行了相关的分析研究,但对双金属管内旋压成形时管材的成形质量以及影响管材成形质量的主要因素相关研究分析较少。
文中采用ABAQUS有限元软件对Al/Cu双金属管内旋压成形进行数值模拟与分析,研究Al/Cu双金属管在内旋压增量成形时的应力、应变、剪切结合强度分布,探究内旋压增量成形时工艺参数:内管减薄率ψ、两管之间的初始间隙c、旋轮进给比f对剪切结合强度的影响规律,获得合理的工艺参数,对内旋压成形工艺有重要的意义。
1 内旋压成形基本原理
双金属管的内旋压成形原理见图1,内旋芯模安装在主轴上,衬管插入基管中,然后装入内旋芯模内,旋轮在主轴的带动下而转动,从而对双金属管进行旋压。在旋压过程中,开始时,衬管发生弹性变形,随着旋轮的不断进入,衬管发生塑性变形,并与基管接触,产生接触压力,基管在力的作用下发生弹性变形,当旋轮从衬管旋出后,由于基管发生弹性变形,衬管发生塑性变形,基管的弹性回复量小于衬管的塑性回复量,因此旋压完成后,两个双金属管紧密地贴在一起。

图1 内旋压成形原理Fig.1 Schematic diagram of inner spinning
2 内旋压成形数值模拟
2.1 有限元模型的建立

图2 有限元模型Fig.2 Finite element model
有限元模型见图2,基管 Cu的尺寸为Φ100 mm×4 mm,衬管5A03Al的尺寸为Φ91 mm×1.2 mm,两管之间的初始间隙c=0.5 mm,旋轮的圆角半径为4 mm,旋轮的轴向进给速度为v=1 mm/s,旋轮绕参考点RP(见图2)旋转,旋转的角速度为ω=20 rad/s。
2.2 材料的定义
基管Cu与衬管Al材料力学性能见表1。在成形过程中,双金属中的衬管发生较大的变形,故采用幂强化材料模型进行计算,幂强化材料模型的数学表达式见式(1)。

式中:K和n为材料参数;K为塑性系数;n为硬化系数。
旋轮在内旋压成形过程中几乎不发生变形,因此可以把其定义为离散刚体。

表1 双金属管材料力学性能参数Tab.1 Mechanical properties of bimetal tube materials
2.3 分析步与相互作用
分析步的步骤设为动力、显式,为了缩短模拟的时间,质量缩放设为100万倍,时间长度设为150 s。在相互作用的创建上,把相互作用属性的类型设为接触,接触的摩擦因数为 0.2,相互作用的类型设为表面与表面接触;在约束的创建上,把双金属管之间的约束类型设为绑定,旋轮的表面耦合到参考点RP上。
2.4 载荷与网络
在载荷的设置上,对于基管与衬管,在管子的起旋端进行固定,固定类型为XSYMM,对于旋轮,由于旋轮的表面耦合到参考点RP上,所以将轴向进给速度设为v=1 mm/s,角速度ω=20 rad/s,加载到参考点RP上。在网格划分上,采用六面体单元对基管和旋轮划分网格;由于衬管在成形过程中变形产生较大的塑性变形,网格可能会产生严重的畸变而破裂,为了保证模拟的顺利进行,对衬管采用 ALE自适应网格划分网格[14]。
3 模拟结果与分析
3.1 内旋压成形应力应变
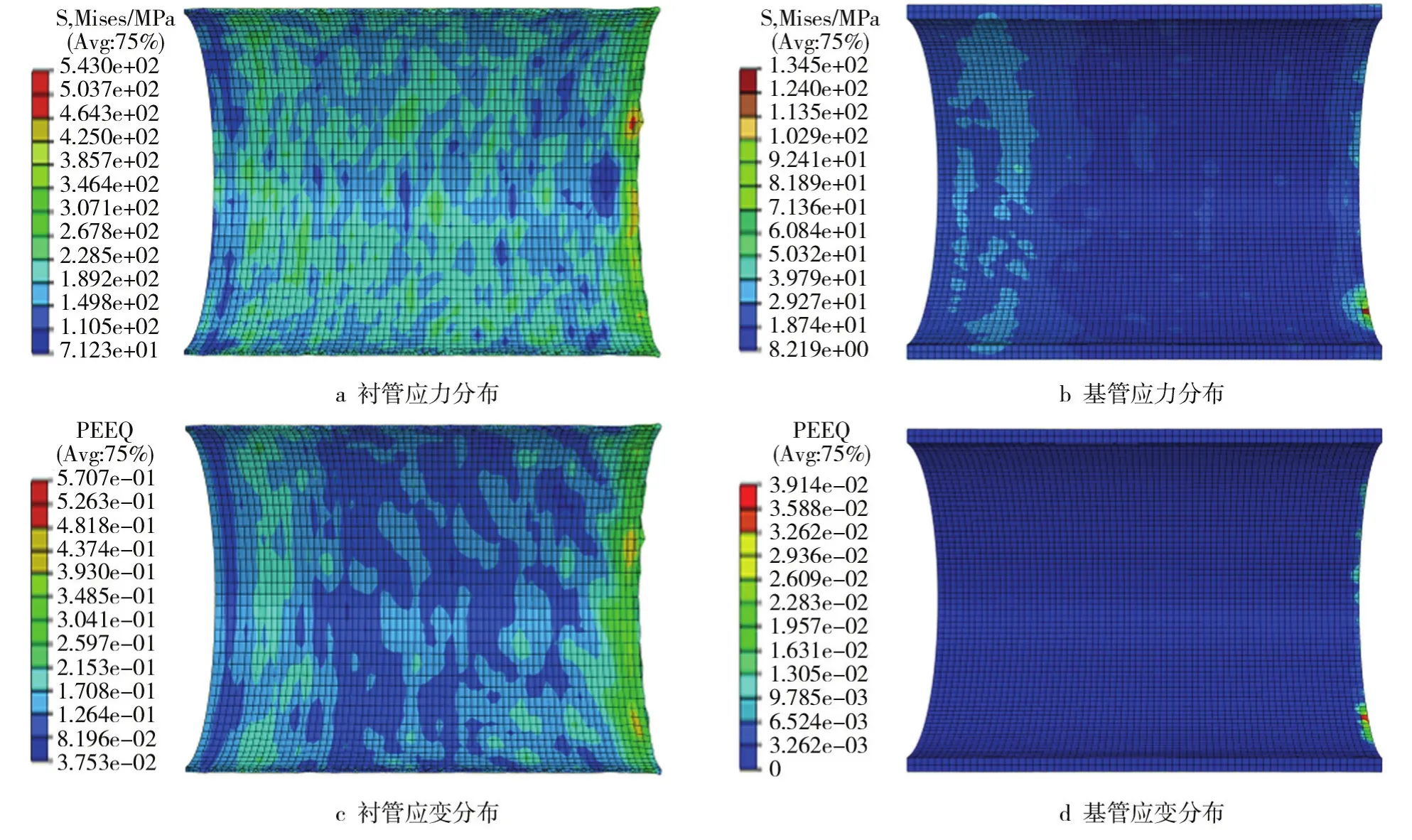
图3 双金属管应力应变分布Fig.3 Stress and strain distribution of bimetal tubes
双金属管在成形过程中,应力应变数值的变化体现出成形的程度,双金属管内旋压有限元仿真结果的应力应变分布见图3。根据图3a—b可以看出,衬管旋压成形后的高应力区出现在旋压结束部分,最大值为543 MPa,主要是由于在旋压成形中,衬管发生较大的塑性变形,由体积不变定理可知,衬管在径向方向的金属流动受到基管的限制,并且旋压的方向是沿轴向运动,因此衬管既有沿径向方向的金属流动,又有沿轴向方向的金属流动,衬管的长度增长,多余的部分没有基管的支撑,因此在旋压结束部分产生高应力区。均匀变形区的应力在110~307 MPa之间,小于衬管的抗拉强度,符合成形条件。基管的高应力区也出现在旋压结束部分,最大值为134 MPa,小于基管的屈服强度,所以基管发生弹性变形。
根据等效塑性应变图3c—d可以看出,衬管旋压成形后的高应变区出现在旋压结束部分,最大值为0.5707,衬管在成形过程中都发生塑性变形。基管只有在旋压结束部分产生了塑性变形,在其他部分的等效塑性应变值接近0,其变形处于弹性变形。
3.2 内旋压成形剪切结合强度
剪切强度是指材料承受剪切力的能力。双金属管的剪切结合强度是指基管与衬管的复合界面承受剪切力的能力。根据CJ/T 192—2017标准规定,基管和衬管的剪切结合强度应不小于0.3 MPa,在ABAQUS模拟中,剪切力的大小用S13, S12,S23来表示,基管和衬管有限元模拟的S13, S12, S23应力分布见图4。由图4a—c可知,衬管均匀变形区的 S13, S12, S23的应力大小分别集中在25, 6.3, 4.6 MPa左右。由图4d—f可知,基管均匀变形区的S13, S12, S23的应力大小分别集中在1.2, 1.55, 5.7 MPa左右。由于衬管发生塑性变形,基管发生弹性变形,因此衬管剪切应力的值大于基管剪切应力的值,基管与衬管的高剪切应力主要集中在旋压结束部分,原因是衬管轴向方向的金属流动,使衬管的长度增长,多余的部分没有基管的支撑,在旋压结束部分造成金属严重挤压、拉长,从而导致产生的剪切应力数值最大。基管与衬管的剪切应力的值都大于0.3 MPa,符合标准。

图4 双金属管的S13, S12, S23应力分布(MPa)Fig.4 S12, S13 and S23 stress distribution of bimetal tube
3.3 旋压工艺参数对剪切结合强度影响
剪切结合强度是双金属管最重要的技术指标,而旋压的工艺参数对剪切结合强度有着显著的影响,因此研究旋压工艺参数对剪切结合强度影响,对材料的成形质量有着重要的作用。
3.3.1 旋轮进给比f
主轴(或芯模)每转一周时,旋轮沿着芯模母线移动的距离称为进给比[15],其相互关系见式(2)。

式中:fv为旋轮与工件接触点沿其母线方向移动的线速度;nm为主轴转速。
在其他旋压工艺参数不变的情况下,改变旋轮进给比f,即设旋轮与工件接触点沿母线方向移动的轴向进给速度vf=1 mm/s不变,分别取角速度ω1=10 rad/s,ω2=20 rad/s,ω3=30 rad/s,ω4=40 rad/s,ω5=50 rad/s,得到f1=0.314 mm/r,f2=0.157 mm/r,f3=0.098 mm/r,f4=0.079 mm/r,f5=0.063 mm/r进行有限元模拟,其剪切应力值主要取决于双金属管S13应力值的大小,其数值平均值分布见图5,由图5可知,随着f的增大,金属管S13应力值也相应增大。由于在成形过程中,进给比增大,旋压过程中的螺距就随着增大,使衬管的塑性变形的速率增加,金属流动的速率增加,从而使基管与衬管之间的径向压力和轴向的剪切应力增大,所以S13的应力值也随着增加。
3.3.2 两管之间的初始间隙c
在其他旋压工艺参数不变的情况下,改变基管与衬管之间的初始间隙c值,对c分别取0.1, 0.2, 0.3, 0.4, 0.5 mm进行有限元模拟,双金属管S13应力平均值分布见图6,由图6可知,随的c的增大,金属管S13应力值也随着增大。由于在成形过程中,两管之间的初始间隙c越大,旋压过程中衬管的扩径量就越大,衬管发生的塑性变形程度就越大,所以产生的残余应力值就越大;基管发生弹性变形、旋压成形后,基管要发生回复,而成形后衬管的回弹程度随初始间隙值增大而减小,增加了基管的回复阻力,所以使基管的残余应力值也增大,从而使基管与衬管之间的径向压力和轴向的剪切应力都增大,所以S13的应力值也随着增加。

图5 不同旋轮进给比下S13应力平均值的分布Fig.5 Average distribution of S13 stress under the change of the feed ratio of the rotary wheel

图6 不同初始间隙下S13应力平均值的分布Fig.6 Average distribution of S13 stress under initial gap change between two tubes
3.3.3 内管减薄率ψ
在旋压过程中,减薄率是变形区的一个主要的工艺参数,直接影响到旋压力的大小和旋压件质量的优劣。壁厚减薄率关系式见式(3)。

式中: 0t为变形前的壁厚(mm);t变形后的壁厚(mm)。
在其他旋压工艺参数不变的情况下,改变内管壁厚减薄率ψ,对ψ分别取25%, 33%, 42%, 50%, 58%进行有限元模拟,双金属管S13应力平均值分布见图7,由图7可知,随着ψ的增大,金属管S13应力值也随着增大。由于在成形过程中,内管减薄率增大,旋压过程中衬管的塑性变形程度随着增大,衬管的径向应力增大,当旋压结束后,衬管的残余应力也增大,从而使基管与衬管之间的径向压力和轴向的剪切应力增大,所以S13的应力值也随着增加。当ψ=58%时,在均匀变形区的应力值在 350 MPa左右,而5A03Al的抗拉强度为320 MPa,其值大于抗拉强度,这样可能会使衬管发生破裂,因此内管的减薄率应小于58%。
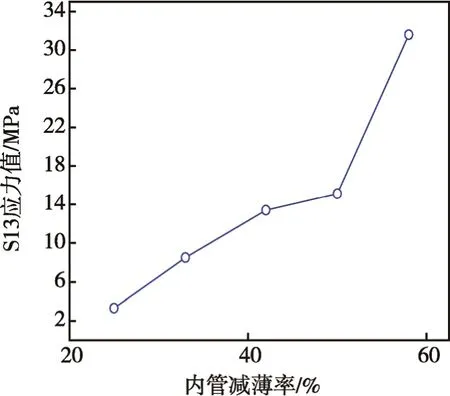
图7 不同内管减薄率下S13应力平均值的分布Fig.7 Average distribution of S13 stress under the condition of inner tube thinning rate change
4 实验
4.1 方案
根据模拟的工艺参数,内管减薄率ψ、两管之间的初始间隙c、旋轮进给比f对成形的剪切结合强度有着显著的影响,所以取3组不同的工艺参数组合作为试样管的工艺参数,试样管的长度为150 mm,具体实验方案见表2。
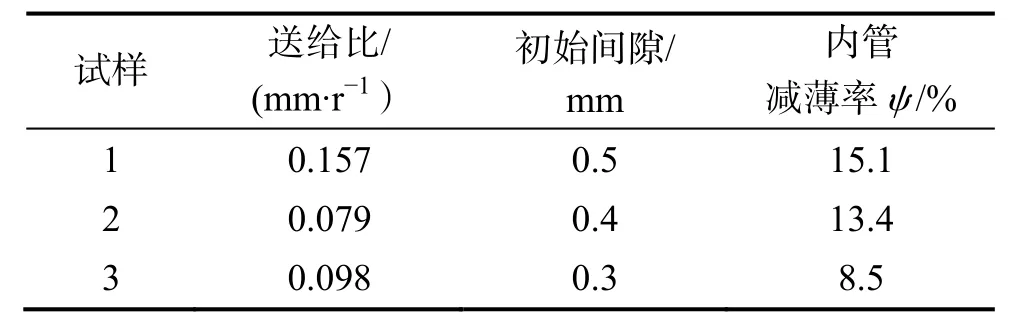
表2 试样管的实验方案Tab.2 Experimental scheme of sample tube
4.2 双金属界面力学性能测试方法
剪切结合强度是双金属管最重要的技术指标,抗剪切强度数值即为剪切力的大小,采用拉伸实验法来测试其界面抗剪切强度。剪切试样见图8。
根据 GB/T 6396—2008复合材料工艺性能实验方法,将剪切试样放入剪切实验装置中,调整实验装置,使试样在实验装置中的间隙为0.1~0.15 mm,用实验机对试样平稳施加实验力,把复材从基材上沿结合面平行剪切下来。抗剪强度按式(4)计算。

图8 剪切试样Fig.8 Shear specimen

本实验中,取b为15 mm,c为2 mm。得到的实验数值与模拟得到的数值见图9,实验的数值与模拟的数值存在一定的偏差,试样 1、试样 2、试样 3的偏差分别为16%, 13%, 17%,在可允许的误差范围内,出现误差的原因是模拟是在理想状态下进行的,而实际的实验,由于管子表面的粗糙度不同,管子的表面可能出现凹陷、凸起、含有其他杂质依附在表面、壁厚不均等缺陷,使其受力不同,应力不均,还有可能是测量的数值存在一定的偏差,使其模拟值与实验值存在一定的偏差。在试样管旋压成形的末端,模拟与实验的剪切应力数值明显增大,主要是由于金属的流动使衬管被拉长,多余的部分没有基管的支撑,末端衬管金属被严重挤压,从而导致产生的剪切应力数值增大。
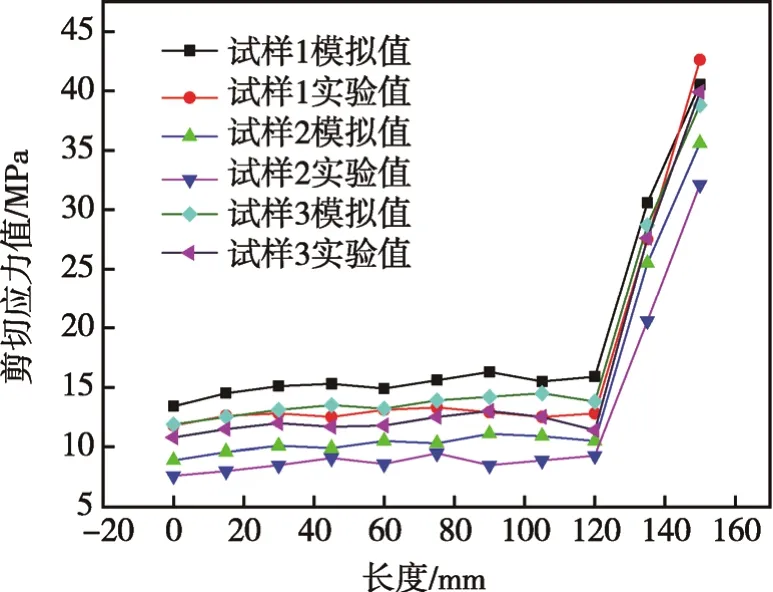
图9 实验与模拟数值分布Fig.9 Numerical distribution of experiment and simulation
5 结论
1) Al/Cu双金属管在内旋压有限元数值模拟中,在其他旋压工艺参数不变的情况下,随着工艺参数内管减薄率ψ、两管之间的初始间隙c、旋轮进给比f的增大,剪切应力数值也随着增大;内管的减薄率应小于58%,否则衬管可能会发生破裂。
2) 剪切应力的实验数值与模拟数值存在一定的偏差,一般在15%左右,在可允许的工程误差范围内,模拟与实验剪切强度应力值集中在8~16 MPa之间,大于CJ/T 192—2017标准规定的0.3 MPa,符合规定要求。
3) 基管与衬管的高剪切应力值主要集中在旋压结束部分,由于衬管径向的扩径量受到限制,根据体积不变定律,衬管金属还会沿着轴向方向流动,使衬管拉长,模拟与实验的剪切应力在旋压成形的末端数值明显增大。
