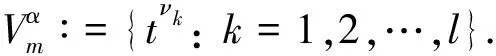求解一类分数阶微分方程终值问题的混合配置法

王林君, 吴 燕, 刘梦雪, 孟义平, 曹明钰

(1. 江苏大学 理学院, 江苏 镇江 212013； 2. 江苏科技大学 理学院, 江苏 镇江 212003；3. 吉林大学 数学学院, 长春 130012)

分数阶微分方程广泛应用于自然界中各种现象的建模和分析中[1-2]. 不同于整数阶微分算子, 分数阶微分算子是非局部的[3], 因此, 分数阶微分方程能更好地模拟自然界的物理现象和动态过程. 例如, 溶质在天然多孔或断裂介质中的平流和分散[4], 在外部影响下模拟黏弹性材料的行为[5], 在数学心理学领域使用分数阶系统模拟人类的行为[6]等. 分数阶微分方程终值问题目前已有很多有效的数值方法： Ford等[7]通过将分数阶微分方程边值问题转化为Fredholm积分方程, 提出了非多项式配置法； Pedas等[8]利用样条配置法求解了一类分数阶微分方程边值问题. 本文针对一类分数阶微分方程终值问题, 给出一种混合配置算法.

考虑如下分数阶微分方程终值问题：

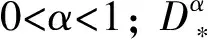
方程(3)-(4)等价于具弱奇核的Volterra积分方程[7]

(5)

在此基础上, 文献[9]结合不动点技巧给出了求解方程(3)-(4)的混合配置格式. 当a>0时, 方程(1)-(2)是终值问题, Ford等[7]证明了其可转化为等价的Fredholm积分方程:

(6)

并给出了其解的存在性定理与唯一性定理.

本文假设方程(1)-(2)满足文献[7,9]的条件, 给出方程(1)-(2)的混合配置解法.

首先, 基于打靶法将方程(1)-(2)转化为初值问题(3)-(4), 步骤如下：

1) 假设初值条件(4)中的初值y0已知, 则用求解分数阶初值问题的混合配置法[9]进行计算便可得到一个含有y0的解y(t,y0)；

2) 根据初值问题的解必经过点(a,ya)从而有y(a,y0)=ya, 故可选用适当的迭代法求解得到y0；

3) 根据得到的y0, 将方程(1)-(2)转化为初值问题(3)-(4).

其次, 在求解初值问题(3)-(4)过程中, 先将方程(3)-(4)转化为方程(5), 然后采用文献[9]中的混合配置法. 令N0表示非负整数集, 对于0<α<1和正整数m, 定义C[0,1]上有限维非多项式子空间[10]

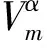
Wα,m={i+jα:i,j∈N0,i+jα

t0j=t0+h0cj,j=1,2,…,l,

其中cj是配置参数, 且满足0≤c1

tik=ti+hidk,k=1,2,…,m,

其中0≤d1

由于方程(5)的解在原点附近具有奇性, 因此混合配置法就是在区间σ0上使用非多项式基底, 而在其他区间使用多项式基底. 定义一个有限维空间

令

z(t)∶=f(t,y(t)),

(7)

将式(7)代入方程(5)得

(8)

将式(8)代入式(7)可得z满足非线性方程

(9)

最后把结果代入式(8)即得方程(5)的解.

注1[9]方程(10)-(11)的性质由f(t,y(t))确定, 当f(t,y(t))关于t和y(t)是线性时, 则得到的方程也是线性的.

例1考虑如下线性分数阶微分方程终值问题[7]：

其真解为

基于打靶法, 首先将其转化为初值问题：

其等价于Volterra积分方程：

表1 例1的数值结果

例2考虑如下非线性分数阶微分方程终值问题:

其真解是y(t)=1-t2.

同理, 首先将其转化为初值问题

(12)

令

(13)

则有

(14)

将式(14)代入式(13)可得

(15)

使用混合配置法求解方程(15), 将得到的解代入式(14), 所得终值问题的数值结果列于表2.

表2 例2的数值结果

表1和表2列出了当m=2, 选取不同的N值时得到的初值条件y0值、误差及收敛阶. 由表1和表2可见, 用混合配置方法求解分数阶微分方程终值问题更有效.