纵向数据下部分线性模型基于经验似然的变量选择

于卓熙, 李梦丽

(吉林财经大学 管理科学与信息工程学院, 吉林省互联网金融重点实验室, 长春 130117)

(1)

目前, 关于模型(1)统计推断问题的研究已有很多结果: 如Fan等[1]对模型(1)的回归系数提出了两种估计方法, 并且对模型(1)的变量选择问题进行了研究； Hu等[2]探讨了模型(1)的核和后移拟合方法； 薛留根等[3]利用经验似然方法给出了模型(1)回归系数置信区间的构造； 张涛等[4]利用分块经验似然方法, 对模型(1)的回归系数提出了一种统计推断方法； 柳长青等[5]基于分块经验似然对模型(1)提出了一个简单有效的检验方法. 上述研究均是针对模型(1)的估计和变量选择问题, 而对其基于经验似然的变量选择问题研究目前文献报道较少. Owen[6-8]提出的经验似然方法在许多方面都优于正态逼近方法, 如不涉及方差估计、由数据自行决定置信域的形状及Bartlett可纠偏等. 由于经验似然有许多类似于参数似然的优良性质[9-12], 所以可以考虑运用基于经验似然的AIC(Akaike information criterion)和BIC(Bayesian information criterion)信息准则进行参数的变量选择, Variyath等[13]已将基于经验似然的变量选择方法用于广义线性模型等可以由一系列估计方程确定的模型中. 本文基于经验似然提出一种纵向数据部分线性模型参数部分的变量选择方法, 并证明其渐近性质. 模拟计算表明, 本文提出的基于经验似然的AIC和BIC信息准则方法具有良好的模型选择效果.

1 主要结果

假设mi是有界的, 即总体的样本容量N与个体数n是同阶的量. 设Tij(i=1,2,…,n;j=1,2,…,mi)是独立同分布(i.i.d.)的, 其共同密度f为Lebesgue可测的.

1.1 回归系数的调整经验似然

在式(1)两边求给定Tij下的条件期望, 并与式(1)两边分别相减可得

Yij-E(Yij|Tij)=[Xij-E(Xij|Tij)]Tβ+εij.

(2)

为构造β的经验似然比函数, 引入辅助变量

其中

(3)

(4)

其中λ=λ(β)是p×1维向量, 且满足

(6)

1.2 基于经验似然的信息准则

令s是{1,2,…,p}的子集, Xij[s]和β[s]分别表示模型(1)中由s确定位置的Xij和β的子向量, 模型(1)的子模型

Yij=(Xij[s])Tβ[s]+θ(Tij)+εij,

(7)

表明只有s确定位置的协变量有显著影响. 令

这里λ[s]=λ(β[s])是s×1维向量, 满足

(9)

再定义

l*(s)=inf{l*(β[s]): β[s]}.

(10)

则基于经验似然的AIC信息准则EAIC(empirical likelihood Akaike information criterion)和BIC信息准则EBIC(empirical likelihood Bayesian information criterion)分别定义为

(11)

这里k是s的基数.

1.3 渐近性质

下面用c表示正常数, 在不同之处可表示不同的值. 假设下列条件成立:

(H1) 带宽满足h=h0N-1/5, 对某个常数h0>0;

(H2) 核K(·)是对称的概率密度函数, 且在其支撑集[-1,1]上有界变差；

(H4) 密度函数f(t)在(0,1)上连续可微, 且存在正的常数d和D, 使得对一切t∈[0,1], 有d≤f(t)≤D;

(H5)θ(t)和μr(t)在(0,1)上二次连续可微,r=1,2,…,p, 其中μr(t)是μ(t)的第r个分量;

(H6) Γ是一个正定矩阵,

(12)

U=B-1-B-1Γ{ΓTB-1Γ}-1ΓTB-1,

(13)

Xi=(Xi1,…,Ximi)T, Ti=(Ti1,…,Timi)T, μ(Ti)=(μ(Ti1),…,μ(Timi))T,

εi=(εi1,…,εimi)T, Wi=diag(ω(Ti1),…,ω(Timi)).

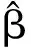
从而

这里:

可以证明

(14)

由文献[3]中引理3知

(15)

取an=op(n1/2), 可知

(16)

在上述计算中把矩阵中的元素由其极限代替, 可得

(17)

(18)

对Q1,n+1(β0,0)运用中心极限定理并由Slutsky定理知结论成立.

类似文献[13]中定理2的证明可得:

类似文献[13]中定理3的证明可得:

定理3假设定理1的条件成立, 若存在{1,2,…,p}的子模型s0是可识别的, 即当且仅当{1,2,…,p}的任意子集s⊃s0时,E(U(β[s]))=0对某些β成立, 则EBIC(s)具有相合性, 而EAIC(s)不具有相合性.

2 算法设计

为说明如何运用基于经验似然的准则EAIC与EBIC实现变量选择, 下面给出变量选择的算法设计. 算法步骤如下：

1) 给定β[s]的初值β0[s], 令λ0=0, c=0, γc=1, ε=10-8;

3) 如果‖Δ(λc)‖<ε, 则转6), 否则转4);

4) 计算δc=γcΔ(λc), 如果R(λc-δc)

5) 更新参数λc+1=λc-δc, c=c+1, γc+1=(c+1)-1/2, 转2);

7) 应用现有的软件包关于β[s]最小化l*(β[s]), 最小化结果即为l*(s);

8) 对所有的s计算l*(s), 用式(11)计算EAIC与EBIC, 选择使EAIC与EBIC达到最小的模型.

3 模拟与应用

3.1 模 拟

为实施模拟, 选择500个数据集, 每个数据集包含n=100个个体, 且每个体具有mi=3次观测, 则总观测数为N=300, 协变量Xij=(X1ij,X2ij,X3ij,X4ij,X5ij)T产生于多元正态分布, 均值为(0,0,0,3,4), 具有协方差结构cov(Xk,Xl)=(0.5)|k-l|,Tij服从(0,1)上的均匀分布, β=(0.5,0.5,0.6,0,0),θ(Tij)=sin(πTij/2), 误差εij服从标准正态分布. 这里核函数取为Epanechnikov核K(u)=0.75(1-u2)+, 权函数ω(t)取为[0.001,0.999]上的示性函数, 带宽h∝N-1/4.

对500个模拟数据集, 给出下列3种情况下, 模型选择的正确率(%)： 1) 选择正确模型(TM)； 2) 包含正确模型, 但至多有1个冗余变量(TM+1)； 3) 包含正确模型, 但至多有2个冗余变量(TM+2). 表1列出了基于AIC与BIC准则的模型选择正确率及基于EAIC与EBIC准则的模型选择正确率. 由表1可见, EAIC与EBIC的模型选择效果优于AIC与BIC的模型选择效果.

表1 不同准则下变量选择的正确率(%)比较

3.2 应 用

选择文献[15]的数据集, 把EAIC与EBIC应用于纵向癫痫病数据研究. 该数据集由6个变量、236个观测值组成, 有59名患者, 每个患者被记录4次, 变量有id(个体识别号)、time(记录时间： 1,2,3,4周)、counts(癫痫发作次数)、treat(治疗： 0为安慰剂; 1为普罗加比)、bcounts(为期8周的基线癫痫发作数)、age(年龄), 因变量是计数变量counts. 本文分别用y,x1,x2,x3,x4表示变量counts,time,treat,bcounts,age, 考虑Poisson广义线性纵向数据模型

lnyij=β0+β1x1ij+β2x2ij+β3x3ij+β4x4ij+εij,i=1,2,…,59,j=1,2,3,4.

研究表明, 变量x2,x4对y的影响不显著, 应用EAIC与EBIC进行变量选择, EACI选择结果包含正确模型, 但有冗余变量x2, 而EBIC选择了正确模型.