Leibniz超代数的非交换张量积

刘贵来, 王 涵, 张庆成

(东北师范大学 数学与统计学院, 长春 130024)

李代数是一类典型的非结合代数, 李超代数是李代数的推广. 目前, 关于李代数和李超代数的研究已有很多结果. 文献[1-2]先后给出了李代数的非交换张量积和李超代数的非交换张量积的概念. 当李代数不必满足反对称性时其即成为Leibniz代数[3-6], Leibniz代数在代数K理论中应用广泛, 文献[7-11]给出了Leibniz超代数的概念及相关性质. Gnedbaye[12]研究了Leibniz代数的非交换张量积. 本文将文献[12]的结果推广到Leibniz超代数上, 使其应用范围更广.

1 Leibniz超代数的作用和半直积

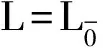
[x,[y,z]]=[[x,y],z]-(-1)|y||z|[[x,z],y],

则称(L,[-,-])为Leibniz超代数.

例11) 对任意一个Leibniz超代数L, 若其满足超反对称性, 即∀x,y∈L, [x,y]=-(-1)|x||y|[y,x], 则L是一个李超代数.

定义2[4]设(L,[-,-])和(L′,[-,-]′)是两个Leibniz超代数, 若f: (L,[-,-])→(L′,[-,-]′)是一个偶的Leibniz超代数线性映射, 且对∀x,y∈L, 满足：

f([x,y])=[f(x),f(y)]′,

则称f: (L,[-,-])→(L′,[-,-]′)是一个Leibniz超代数的同态映射.

定义3[8]设L是一个Leibniz超代数, 若存在L的一个2-阶化线性子空间H, 使得对∀x,y∈H, 有[x,y]∈H, 则称H是一个Leibniz超子代数.

如果H是L的一个2-阶化线性子空间, 且对∀x∈H,y∈L, 有[x,y]∈H, [y,x]∈H, 则称H是L的阶化Leibniz理想. 此时L/H继承了Leibniz超代数的结构, 称为Leibniz超商代数.

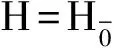
定义5[9]令L是一个Leibniz超代数, 其超子空间Z(L)={x∈L|[x,y]=[y,x]=0, ∀y∈L}称为L的中心.

定义6设L和M是两个Leibniz超代数, 若存在一个对偶的双线性映射λ:L⊗M→M使得λ(x⊗m)=xm及ρ:M⊗L→M使得ρ(x⊗m)=mx, 对任意齐次元素x,y∈L和m,m′∈M, 下列条件成立：

1)m[x,y]=(mx)y-(-1)|x||y|(my)x；

2)[x,y]m=(-1)|m||y|(xm)y-(-1)|m||y|x(my)；

3)x(ym)=-(-1)|m||y|x(my)；

4)x[m,m′]=[xm,m′]-(-1)|m||m′|[xm′,m]；

5) [m,m′]x=(-1)|x||m′|[xm,m′]+[m,m′x]；

6) [m,xm′]=-(-1)|x||m′|[m,m′x].

则称其为从L到M的Leibniz作用.

在上述条件下, 如果对∀x∈L,m∈M, 有xm=0=mx, 则称Leibniz作用是平凡的.

例21) 令L和H分别是Leibniz超代数K的Leibniz超子代数和阶化Leibniz理想, 定义括积为K中的括积运算, 则存在一个从L到H的Leibniz作用.

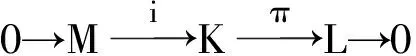
(1)

(2)

则存在从L到M的Leibniz作用.

定义8设L和M是两个Leibniz超代数, 存在L到M上Leibniz作用及一个同态映射∂:M→L, 如果对任意齐次元素x∈L和m,m′∈M, 满足下列条件：

1) ∂(xm)=[x,∂(m)]；

2) ∂(mx)=[∂(m),x]；

3)∂(m)m′=[m,m′]；

4)m∂(m′)=[m,m′].

则称该同态映射为Leibniz超代数的交叉模.

2) 设L和M是两个Leibniz超代数, 存在L到M的Leibniz作用, 则平凡映射0:M→L是Leibniz超代数交叉模.

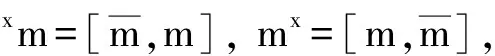
定理1设L和M是两个Leibniz超代数, ∂:M→L是一个Leibniz超代数交叉模, 则下列结论成立：

1) Ker ∂⊆Z(M)；

2) Im ∂是L的一个阶化Leibniz理想；

3) Leibniz超代数Im ∂平凡地作用于Z(M)和Ker ∂.

证明： 1) 对∀m∈Ker ∂, 有∂(m)=0, 则由定义8中3)和4)知, 对∀m′∈M, 有

∂(m)m′=[m,m′]=0,m′∂(m)=[m′,m]=0,

所以m∈Z(M), 于是结论成立.

2) 对∀x∈Im ∂⊂L及∀y∈L, 存在m∈M, 使得∂(m)=x, 则有

[x,y]=[∂(m),y]=∂(my)∈Im ∂, [y,x]=[y,∂(m)]=∂(ym)∈Im ∂,

结论成立.

3) 对∀x∈Im ∂, 存在m∈M, 使得∂(m)=x; ∀m′∈Z(M), 有

xm′=∂(m)m′=[m,m′]=0,m′x=m′∂(m)=[m′,m]=0,

于是Leibniz超代数Im ∂平凡地作用于Z(M), 又由1)知, Leibniz超代数Im ∂也平凡地作用于Ker ∂.

2 主要结果

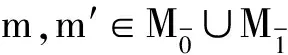
则称Leibniz作用是相容的.

例4设H和H′是Leibniz超代数L的阶化Leibniz理想, 则H和H′之间的相互Leibniz作用是相容的.

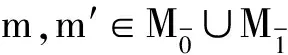
则称(L,h1,h2)是一个Leibniz超对.

例5设M和N是Leibniz超代数L的两个阶化Leibniz理想, 令A=M∩N, 且定义双线性映射h1:M×N→A和h2:N×M→A, 满足h1(m,n)=[m,n],h2(n,m)=[n,m], 则(A,h1,h2)是一个Leibniz超对.

如果存在广泛的Leibniz超对, 则在同构意义下唯一确定. 下面刻画Leibniz超代数的非交换张量积.

定义12设M和N是域K上的两个Leibniz超代数, 且彼此有Leibniz作用, 令V是所有形如m*n和n*m的元素生成的2-阶化向量空间, 其中且|m*n|=|m|+|n|. 若对∀下列条件成立：

1)λ(m*n)=λm*n=m*λn,λ(n*m)=λn*m=n*λm;

2) (m+m′)*n=m*n+m′*n,n*(m+m′)=n*m+n*m′,

m*(n+n′)=m*n+m*n′, (n+n′)*m=n*m+n′*m;

3)m*[n,n′]=mn*n′-(-1)|n||n′|mn′*n,n*[m,m′]=nm*m′-(-1)|m||m′|nm′*m,

[m,m′]*n=(-1)|m′||n|mn*m′-(-1)|m′||n|m*nm′,

[n,n′]*m=(-1)|m||n′|nm*n′-(-1)|m||n′|n*mn′;

4)m*m′n=-(-1)|m′||n|m*nm′,n*n′m=-(-1)|m||n′|n*mn′;

5)mn*m′n′=[m*n,m′*n′]=mn*m′n′,mn*n′m′=[m*n,n′*m′]=mn*n′m′,

nm*n′m′=[n*m,n′*m′]=nm*n′m′,nm*m′n′=[n*m,m′*n′]=nm*m′n′.

其中:m,m′的阶相同;n,n′的阶相同. 则V是一个Leibniz超代数, 并将其重新定义为Leibniz超代数M和N的非交换张量积M*N.

注1若Leibniz超代数的非交换张量积满足反对称性m*n=-(-1)|m||n|n*m, 则其为李超代数的非交换张量积.

定理2若Leibniz超代数M和N彼此平凡作用, 则M*N是一个交换Leibniz超代数, 且存在一个同构映射：

M*N≅(Mab⊗Nab)⊕(Nab⊗Mab),

其中:Mab=M/[M,M];Nab=N/[N,N].

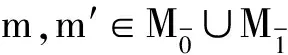
m*[n,n′]=[m,m′]*n=[n,n′]*m=n*[m,m′]=0,

于是M*N与(Mab⊗Nab)⊕(Nab⊗Mab)同构, 结论成立.

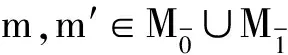
f(nm)=g(n)f(m),f(mn)=f(m)g(n),g(mn)=f(m)g(n),g(nm)=g(n)f(m),

则存在一个Leibniz超代数的同态： f*g: M*N→M′*N′, 满足

(f*g)(m*n)=f(m)*g(n), (f*g)(n*m)=g(n)*f(m).

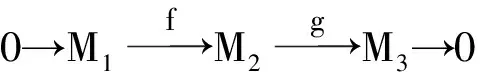
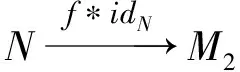
证明： 显然g*idN是一个满同态, 且Im(f*idN)⊆Ker(g*idN).而Im(f*idN)是所有形如f(m1)*n,n*f(m1)的元素生成的, 其中齐次元素m1∈M, n∈N. 由于对任意齐次元素m1∈M1, m2∈M2, n1,n2∈N, 均有

则Im(f*idN)是M2*N的一个阶化Leibniz理想. 因此g*idN诱导了一个Leibniz超代数同态：

ξ: (M2*N)/Im(f*idN)→M3*N,

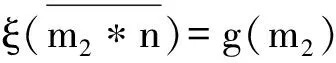
ξ-1:M3*N→(M2*N)/Im(f*idN),

定理4设L是一个Leibniz超代数, M是其阶化Leibniz理想, 则存在一个Leibniz超代数短正合列：

τ′: (L/M)*(L/M)→(L*L)/Im(σ),

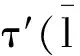
定理5设M和N是两个Leibniz超代数, 且彼此的Leibniz作用相容, 则有：

1) 存在Leibniz超代数的同态映射：

2)Ker(ψM)⊆Z(M*N),Ker(ψN)⊆Z(M*N).

则ψM[m1*n1,m2*n2]=[ψM(m1*n1),ψM(m2*n2)]； 又有

则ψM[m1*n1,n2*m2]=[ψM(m1*n1),ψM(n2*m2)]； 又有

则ψM[n1*m1,m2*n2]=[ψM(n1*m1),ψM(m2*n2)]； 又有

则ψM[n1*m1,n2*m2]=[ψM(n1*m1),ψM(n2*m2)]； 又有

则ψN[m1*n1,m2*n2]=[ψN(m1*n1),ψN(m2*n2)]； 又有

则ψN[m1*n1,n2*m2]=[ψN(m1*n1),ψN(n2*m2)]； 又有

则ψN[n1*m1,m2*n2]=[ψN(n1*m1),ψN(m2*n2)]； 又有

则ψN[n1*m1,n2*m2]=[ψN(n1*m1),ψN(n2*m2)]. 综上可得结论.

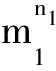
若n1*m1∈Ker(ψM), 即ψM(n1*m1)=n1m1=0, 则对∀m2*n2,n2*m2∈M*N, 有

因此Ker(ψM)⊆Z(M*N).

若m1*n1∈Ker(ψN), 即ψN(m1*n1)=m1n1=0, 则对∀m2*n2,n2*m2∈M*N, 有

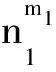
因此Ker(ψN)⊆Z(M*N).