局部小范围闭合等值线命题规律及其教学启示

2018-07-19广西

教学考试(高考地理) 2018年2期

关键词：等值线等温线命题

广西

侯刘起李帅

局部小范围闭合等值线是指相邻的两条等值线之间呈闭合形状的等值线，是等值线的重要内容。等值线部分是地理教学的重点、难点，也是高考的高频考点。本文结合高考题、模拟题中的典型例题，梳理局部小范围闭合等值线的命题规律，并从中总结，得到教学启示。

一、局部小范围闭合等值线的命题规律

局部小范围闭合等值线的考查包括闭合线上数值的判读、闭合线内数值的判读两个方面。

1.闭合线上数值的判读

闭合线上数值的判读包括相邻两条等值线的数值相等、相邻两条等值线的数值不相等两个方面。当相邻两条等值线的数值相等时，闭合线上的数值可以按照等值线的变化规律(增大或减小)直接进行判读(见例1)。当相邻两条等值线的数值不相等，且无附加条件时，闭合线上的数值与相邻两条等值线的数值相等(见例2)。当相邻两条等值线的数值不相等，且有地形等附加条件时，闭合线上的数值与相邻的某一条等值线的数值相等(见例3)。

【例1】林线是高山垂直自然带谱中一条重要的生态界限，通常是指高海拔处树木(针叶林)生长的上限。下图示意我国局部区域高山林线海拔分布。图中M地的林线海拔可能为______米。

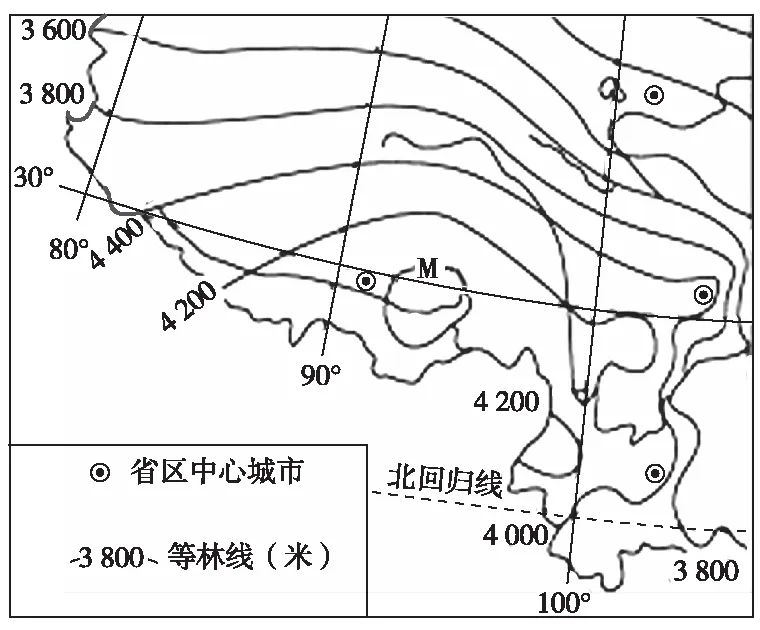
【解析】该题目以我国局部地区为背景，考查林线的判读。从图中可以看出，M地两侧等值线的数值相等，等值线的间距为200米。因此，按照等值线的变化规律，直接读出M地的林线海拔为4 400米。

【例2】(2002年全国大纲卷)“某时海平面平均气压图”中M处的气压数值可能为 ( )

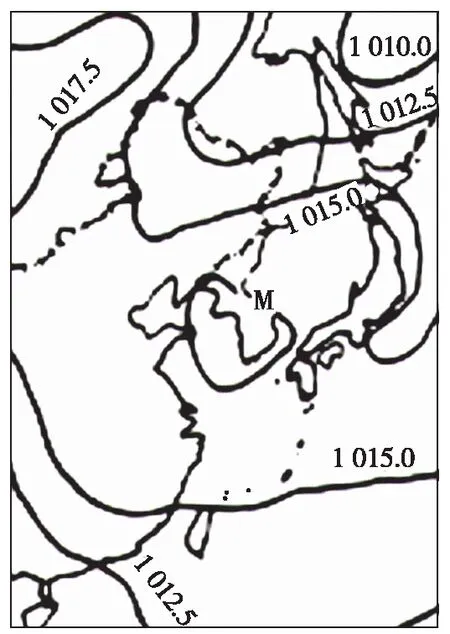
C.1 017.5、1 015 D.1 015、1 012.5

【解析】该题目以东亚为背景，考查气压值的判读。从图中可以看出，M地两侧等压线的数值不相等。首先找到M地附近数值不相等的两条等压线分别是1 015 hPa、1 017.5 hPa。那么M地的数值与相邻的两条等值线的数值相等，为1 015 hPa或1 017.5 hPa,故选C。

【例3】“北美部分地区七月等温线分布图”中等温线M的数值为______℃，请说出判断理由。

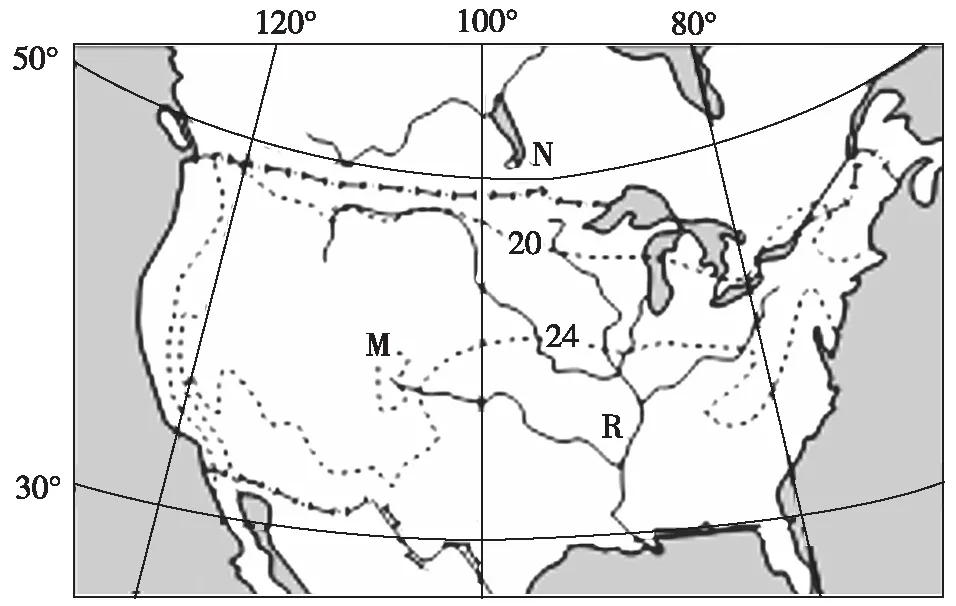
【解析】该题目以北美洲为背景，考查气温的数值及其理由。从图中可以看出，M地两侧等温线的数值不相等。首先找到M地两侧数值不相等的两条等温线，分别是20℃、24℃。那么M地的数值与相邻的两条等温线的数值相等，为20℃或24℃。但是，M地位于美国西部山地地区，海拔较高，气温较低，因此M地气温为20℃。

2.闭合线内数值的判读

闭合线内数值的判读包括相邻两条等值线的数值相等、相邻两条等值线的数值不相等两个方面。当相邻两条等值线的数值相等时，闭合线内的数值可以按照等值线的变化规律(增大或减小)直接进行判读，但要注意附加条件(见例4)。当相邻两条等值线的数值不相等，闭合线上有数值且无附加条件时，可以根据“大大小小规律”(大于大的，小于小的)直接判读闭合线内的数值，且结果只有一种(见例5)。当相邻两条等值线的数值不相等，闭合线上无数值且无附加条件时，可以根据“大大小小规律”(大于大的，小于小的)判读闭合线内的数值，但结果有两种(见例6)。当相邻两条等值线的数值不相等，闭合线上无数值但有地形、洋流等附加条件时，要首先根据“大大小小规律”(大于大的，小于小的)判读闭合线内的数值，然后再根据附加条件确定最终结果(见例7)。

【例4】下图是我国某区域等高线地形图，图中②地的海拔可能是 ( )

下面以“篮球双手胸前传接球”一课为例，谈谈“一二·三六”教学模式的具体实施。本节课主要围绕着动作技术和合作意识两条主线展开，要求各个学生需要通过感受练习过程中产生的接球、抱球以及传球等各种判断产生的一连串问题及两者之间相互体谅、相互理解、相互配合，进行深入的探究、合作、思考、汇总，然后基于自身的实践去了解前后站、接与抱以及平行站之间存在的差异性，最终掌握教学要求的技术内容。

A.750米 B.750～780米

C.780～810米 D.810米

【解析】该题目以我国某区域为背景，考查等高线的判读。从图中可以看出，等高线的间距为30米，②地闭合线两侧等高线的数值相等，并且②地周围有河流流过。因此，按照等高线的变化规律及河流的地形特征，可以读出②地闭合线上的海拔为780米，并且②地的海拔高于闭合线上的海拔，所以②地的海拔大于780米，小于810米，故选C。

【例5】(2011年福建卷)气温、降水量和日照时数过高或过低都会给柑橘的生长发育带来风险，气候风险度越大，柑橘减产的可能性也越大。下图示意我国大陆亚热带柑橘产地气候风险度分布。图中E、F两地气候风险度分别可能为 ( )

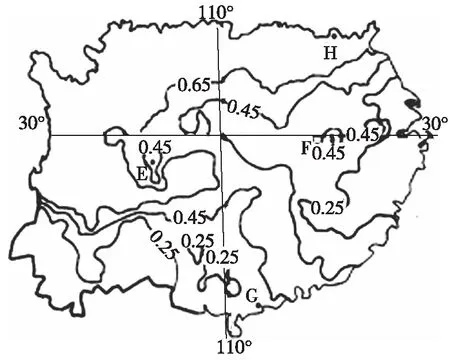
A.0.55 0.50 B.0.30 0.50

C.0.55 0.35 D.0.30 0.35

【解析】该题目以中国东南地区为背景，考查气候风险度的判读。从图中可以看出，E、F闭合线两侧等值线的数值不相等。E地闭合线两侧数值不相等的两条等值线数值为0.45、0.65，F地闭合线两侧数值不相等的两条等值线数值为0.25、0.45，同时E、F两地闭合线上的数值都为0.45。因此，根据“大大小小规律”判断，E地的数值小于0.45，F地的数值大于0.45，故选B。

【例6】(2013年全国大纲卷)某种生物的种密度指单位面积该种生物的个体数量。下图为北美洲部分地区某种动物的种密度等值线图。H、K、Q、R四地中，该种动物的种密度可能相等的两地是 ( )

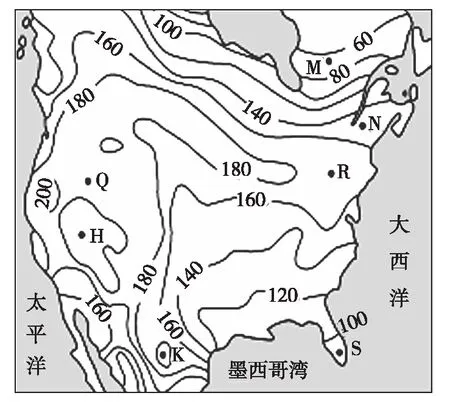
A．H、R B．Q、R C．Q、H D．H、K

【解析】该题目以北美洲为背景，考查生物种密度的判读。从图中可以看出，Q地的数值大于180，小于200；R地的数值大于160，小于180；H、K闭合线两侧等值线的数值不相等。首先找到H地闭合线两侧数值不相等的两条等值线为180、200，K地闭合线两侧数值不相等的两条等值线为160、180。那么H地闭合线上的数值可能为180或200，K地闭合线上的数值可能为160或180。然后，根据“大大小小规律”判断出H地的数值大于200、小于220或大于160、小于180；K地的数值大于180、小于200或大于140、小于160。经对比可知，Q、K或者H、R的动物种密度可能相等，故选A。

【例7】下图是南美洲南部地区示意图，图中M处的温度值应为 ( )

A.20℃

C.16℃

【解析】该题目以南美洲为背景，考查温度的判读。从图中可以看出，M地闭合线两侧等温线的数值不相等。首先找到M地闭合线两侧数值不相等的两条等温线为16℃、20℃，那么M地闭合线上的数值与相邻的两条等温线的数值相等，为16℃或20℃。其次，根据“大大小小规律”判断出M地的数值可能小于16℃或大于20℃。但是，由于M地位于安第斯山脉且受沿岸秘鲁寒流的影响，因此,M地的温度大于12℃，小于16℃,故选B。

二、基于命题规律的局部小范围闭合等值线教学启示

结合典型例题,对局部小范围闭合等值线命题规律进行梳理，得到以下教学启示。

1.关注命题规律，加强数值判读

局部小范围闭合等值线的命题以数值判读为主，但是，数值判读的要求略有变化。例如例1、例2、例3是局部小范围闭合等值线线上数值的判读，而例4、例5、例6、例7是局部小范围闭合等值线线内数值的判读。另外，例1、例2、例4、例7只判读一条闭合线的数值；例5判读两条闭合线的数值；例6判读两个常规的数值、两条闭合线的数值并进行比较；例3判读一条闭合线的数值，并说出理由。

因此，在教学过程中，要注重引导学生观察，是局部小范围闭合等值线线上数值的判读还是线内数值的判读。同时，要引导学生不仅学会判读一条局部小范围闭合等值线数值，也要进一步引导学生关注多条局部小范围闭合等值线数值的判读、局部小范围闭合等值线数值与常规数值的比较以及局部小范围闭合等值线的成因等。

2.注重方法指导，强化迁移应用

在局部小范围闭合等值线的典型例题中，既包括等压线、等温线、等高线等常见的等值线类型，也包括气候风险度、生物种密度、林线等不为人熟知的等值线类型。但是，局部小范围闭合等值线的判读方法是相同的，即首先判断是闭合线上还是闭合线内数值的判读,然后观察与闭合线相邻的两条等值线的数值是否相等。当相邻两条等值线的数值相等时，闭合线上、闭合线内的数值可以按照等值线的变化规律(增大或减小)直接进行判读。当相邻两条等值线的数值不相等时，闭合线上的数值有两种情况，即当无附加条件时，闭合线上的数值与相邻的两条等值线的数值相等；当有地形等附加条件时，闭合线上的数值与相邻的某一条等值线的数值相等。

当相邻两条等值线的数值不相等时，闭合线内的数值有三种情况，即当闭合线上有数值且无附加条件时，可以根据“大大小小规律”(大于大的，小于小的)直接判读闭合线内的数值，且结果只有一种；当闭合线上无数值且无附加条件时，可以根据“大大小小规律”判读闭合线内的数值，但结果有两种；当闭合线上无数值但有地形、洋流等附加条件时，要首先根据“大大小小规律”(大于大的，小于小的)判读闭合线内的数值，然后再根据附加条件确定最终结果。

因此，在教学过程中，要指导学生牢固掌握局部小范围闭合等值线的判读方法。同时，结合命题规律对局部小范围闭合等值线从不同角度、不同侧面、不同情形、不同背景等进行变式训练，从而强化知识、方法的迁移应用，达到举一反三、融会贯通的效果。