一种基于特征的协同聚类模型

张 飞 张立波 罗铁坚 武延军

1(中国科学院大学 北京 101408) 2 (中国科学院软件研究所 北京 100190) (tjluo@ucas.ac.cn)

互联网的蓬勃发展促使信息总量呈现指数上升，这使得互联网用户从庞杂的信息中获取有用的信息变得越来越困难.推荐系统能够根据用户的特点和兴趣有针对性地为他们推荐有价值的信息.因此推荐系统的作用越来越突出，已经被应用到商品推荐等诸多领域中.

协同过滤(collaborative filtering, CF)[1-3]算法是推荐系统中一种被广泛采用的算法.与传统基于内容(content-based)[4]的推荐算法不同，协同过滤算法不需要用户的个人资料以及物品本身的信息，仅仅利用用户和物品之间的交互关系(如点击、浏览、评分等)就能做出准确的推荐.在用户越来越重视个人信息安全的形势下，协同过滤算法相比基于内容的推荐算法具有更大的优势.

传统的协同过滤算法在取得一定性能的同时仍然存在一些问题.例如数据的高稀疏性使得算法的推荐性能难以提高，对此研究人员提出一种基于聚类的协同过滤算法，通过对用户和物品进行聚类，将有相同爱好的用户和相同特征的物品分为一组，然后在各个分组上分别利用协同过滤算法进行推荐.但是，大部分聚类方法都只允许用户或者物品属于一个分组，而现实中一个用户可能有多种爱好并且一个物品可能具备多种特征，因此只允许用户和物品属于一个分组具有很大的局限性.

基于上述考虑，本文提出了一种基于特征的协同聚类模型，它充分利用用户与物品之间的交互信息来挖掘它们的潜在特征，并根据这些特征将他们分配到合适的多个分组中.例如某用户同时喜欢喜剧电影与动作电影，则应该将该用户分配到喜剧和动作这2个分组中去.这种聚类方式充分利用了用户和物品的特征，使得聚类的结果更加可信.最后将本文算法得到的聚类结果使用传统的协同过滤算法进行推荐，通过与多种最新算法在3种公开数据集上的比较，验证了本文提出的模型能够显著提高预测与推荐的准确度.

本文的主要贡献有2个方面：

1) 提出一种快速提取用户以及物品特征的方法以及给出该方法的求解过程；

2) 提出一种图模型将用户评分信息与特征信息结合，用来计算最终的聚类结果.

1 相关工作

Breese等人[5]将协同过滤推荐算法分为2种类型:基于内存(memory-based)的协同过滤算法与基于模型(model-based)的协同过滤算法.

基于内存的协同过滤算法主要是通过寻找用户[6]或者物品[7]之间的相似性来进行推荐，虽然这种推荐系统实现简单并且很有效，但是它还存在很多问题，比如无法有效处理大规模数据以及高稀疏性的数据.为了解决基于内存的协同过滤算法的这种问题，许多基于模型的协同过滤算法被提出，比如贝叶斯模型[8]、基于回归的模型[9]、潜在语义模型[10]、聚类模型[11-12]和矩阵分解模型[13].在这些模型中，矩阵分解模型被广泛使用，比如著名的SVD(singular value decomposition)[14]模型、NMF(non-negative matrix factorization)[15]模型、MMMF(maximum margin matrix factorization)[16]、NPCA(nonparametric probabilistic principal component analysis)[17]等，它们在处理大规模数据时有着杰出的表现，但是推荐系统数据高稀疏性的特点仍旧限制了这些算法性能.

为了克服数据的高稀疏性等问题，基于聚类的协同过滤算法被提出.聚类的协同过滤算法首先将用户与物品进行适当的聚类分组，然后在每个分组上分别使用协同聚类算法进行推荐.由于互联网的发展，越来越多的算法在对用户物品进行聚类时，加入了很多额外的信息来增强聚类性能[18-22]，比如产品分类信息[23]、用户信任网络[24]等.但是这些额外的信息有时候并不能增加聚类的准确度，比如某用户购买了某件商品，他的好友们可能不会对这件商品感兴趣，因此本文的聚类过程仅仅使用了隐式反馈信息，如用户物品评分.这种只使用隐式反馈信息的聚类算法一般分为3种:基于用户的聚类、基于物品的聚类以及双侧聚类.

基于用户的聚类算法是根据用户的相似度将最相似的若干用户分为一组，在为具体的用户进行推荐时只考虑用户所在的分组.例如Sarwar等人[25]就是将全部的用户根据相似度进行聚类，并将每一个聚类结果中的用户视为邻居；Xue等人[26]则是通过训练数据将用户进行聚类，为每个用户挑选出最好的若干邻居并学习出预测矫正信息，然后利用这些矫正信息以及邻居来为具体的用户进行推荐；相反，基于物品的聚类算法则是根据物品之间的相似度来进行聚类，例如O’Connor等人[27]提出的方法.

除了上述的一些单侧聚类算法外，还有一些基于双侧聚类的聚类算法，这与本文的主要方法一致，Ungar等人[28]通过使用吉比斯采样与k-means方法对用户与物品进行聚类，该方法在模拟数据上有一定的效果，但是在真实数据上却不乐观；George等人[29]则是对用户物品同时聚类，然后根据聚类分组中的平均打分以及用户自身的矫正量来进行最后的推荐；除了以上这些单类聚类算法外，Xu等人[30]还提出了一种多类协同聚类算法，它与本文核心思想一致：允许用户和物品同时属于多个分组.但是它的聚类原理比较片面，仅仅考虑用户对物品的评分而忽略了用户自身的特点与物品自身的特点.

2 基于特征的协同聚类模型

本文提出的基于特征的协同聚类算法主要框架及其在推荐系统中的作用如图1所示，主要包括2个模块：1)一个特征表示模型，用来挖掘用户的兴趣以及物品的特征;2)一个图模型，利用挖掘出来的特征以及用户的评分信息计算最终的聚类结果.在推荐系统中，可以先利用本文算法完成数据的聚类工作，再将聚类的结果应用到推荐模型中，从而提高最终的推荐性能.

2.1 相似度的计算

通过图1可以发现在本文模型中需要计算用户相似度与物品相似度，在推荐系统中，著名的基于相似度的推荐算法如Item-Based[7]，User-Based[6]等所采用的相似度算法主要是余弦相似度、Pearson相关系数以及约束Pearson相关系数等，它们的计算方法如表1所示.

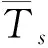
从表1可以看出，当Ist=∅时,也即用户s和t之间不存在共同打分过的物品，那么这3种相似度算法都无法计算s和t的相似度;另一方面当2个用户共同打分过的物品较少甚至只有1个时，仅仅利用这些少量的打分信息来判断用户之间的相似度显然是不够准确的.而在推荐系统中，其数据的高稀疏性是其最大的特点，2个用户之间共同打分过的物品集合Ist往往都比较少甚至为空，因此，采用上述方法计算得到的相似度不够可靠，为了解决这个问题，本文采用一种新的特征表示模型来挖掘用户以及物品的特征信息，然后用这些特征信息来计算相似度，我们将在2.2节讨论如何提取特征.

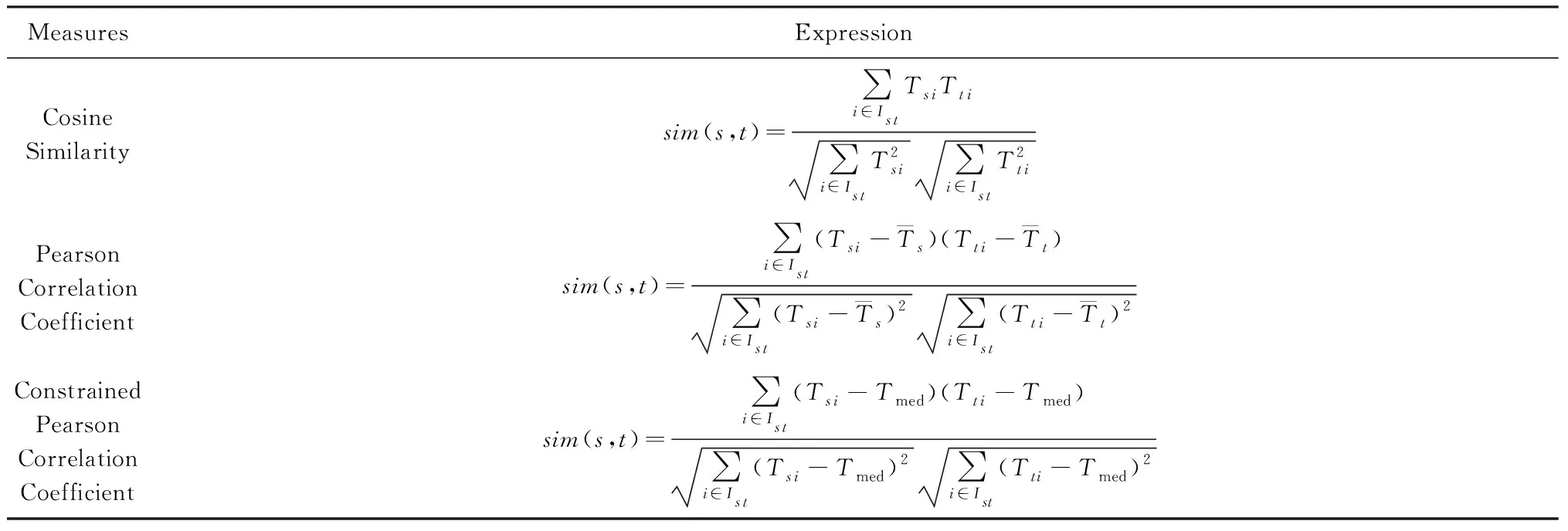
Table 1 Measures of Similarity[31]表1 相似度的计算方法[31]

2.2 特征信息的提取

在本节我们将介绍图1中的特征表示模块，该部分用来提取用户与物品的特征以便计算它们的相似度.

设n个用户对m个物品的评分矩阵为T∈n×m，用户的特征信息矩阵为U∈n×a，其中第u行的a维行向量Uu表示第u个用户的特征信息向量,a为一个较小的指定的特征信息维度;同样地，用矩阵V∈m×b表示全部物品的特征信息矩阵，b表示物品特征信息的维度.我们将通过二次回归模型用第u个用户的特征信息Uu以及第v个物品的特征信息Vv去拟合评分Tu v.

在传统的二次回归模型中，对于特征向量x，其对应的监督值y通过表达式去拟合：

(1)

其中,z表示常数项系数，w表示一次项系数，W表示二次项系数，l则表示向量x的维度.则在本文的模型中，显然有x=(Uu,Vv)，y=Tu v，于是得到：

(2)

我们令：

(3)

(4)

可以观察到，pu只和用户u有关，qv只和物品v有关，于是我们得到最终的二次回归模型：

(5)

注意到此处我们重新定义W∈a×b.式(5)表示用户u对物品v的评分可近似由1个全局常数z、1个与用户有关的常数pu、1个与物品有关的常数qv、以及他们的特征元素之间的两两乘积的加权和组成.所以，我们可以令z为整个数据集评分的均值，令pu为用户u的全部评分的均值，令qv为物品v被评分的均值，即：

(6)

(7)

(8)

其中,当Tu v=0时表示用户u对物品v的评分不存在，此时δu v=0，否则δu v=1.

根据式(5)我们可以得到模型的拟合误差：

(9)

优化式(9)使得L最小即可得到我们所需的特征信息矩阵U和V.我们利用随机梯度下降法求解，并设学习率为η，我们得到参数更新公式：

(12)

下面给出本文提取特征的算法的伪代码，如算法1所示：

算法1. 特征提取算法.

输入：评分矩阵T、参数n,m,a,b,η；

输出：矩阵U,V.

① 随机初始化W,U,V；

② 根据式(6)计算z；

③ foru=1 tondo

④ 根据式(7)计算pu；

⑤ end for

⑥ forv=1 tomdo

⑦ 根据式(8)计算qv；

⑧ end for

⑨ repeat

最终得到U,V矩阵即可表示为用户和物品的特征信息矩阵，然后利用表1中的相似度算法就能够得到用户以及物品的特征信息相似度.

2.3 图模型的构建

在本节我们将介绍图1中的图模型模块，将2.2节计算得到的相似度与用户的评分信息结合构建出一个无向图，利用它来计算最终的聚类结果.

在我们的图模型中，所有的顶点由用户和物品组成，边则分别由3部分构成:用户相似度、物品相似度以及用户对物品的评分.另外，为了强调高评分在图中的重要性，有变换函数：

f(Tu v)=(1+e-τ(Tu v-Tmed))-1，

(13)

其中,Tmed表示评分制的中值，τ为超参数.该函数的作用是将中值映射为权重值0.5，当评分高于中值时，表示用户对该物品有喜欢的倾向，因此在聚类中应该有较高权重，但同时弱化高评分之间的差距，比如4分与5分的权重差距显然应该小于4分与3分之间的差距，同理，评分小于中值时应该具有较低的权重，且同样需要弱化低评分之间的权重差距.

因此，该图模型的构建过程如下:

1)n个用户与m个物品组成n+m个节点，用户节点编号为1,2,…,n，物品节点表示为编号n+1,n+2,…,n+m，第v个物品编号为n+v；

2) 用户u与物品v之间边的权值定义为Wu(n+v)=f(Tu v)；

3) 用户i与用户j之间边的权值定义为Wi j=α×sim(Ui,Uj)，其中α表示放缩因子，其目的是为了均衡用户评分所转化的权值与根据相似度得到的权值之间的差异，函数sim(Ui,Uj)表示用户i与用户j之间的特征信息相似度，可以采用表1中的相似度算法计算，本文采用的是余弦相似度算法；

4) 物品i与物品j之间边的权值定义为W(n+i)(n+j)=β×sim(Vi,Vj)，函数sim(Vi,Vj)表示物品i与物品j之间的特征信息相似度，参数β也是放缩因子，为了平衡物品相似度与评分权值之间的差异.

通过上述步骤构建好图模型后，便得到该无向图的权值矩阵W∈(n+m)×(n+m)，下面讨论如何利用它得到最终的聚类结果.

2.4 聚类结果的计算

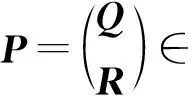
显然，在2.3节的图模型中，权值越大的边对应的2个顶点，表明用户对该物品更加关注或者用户之间、物品之间更加相似，它们应该更有可能被分在同一组中，即它们在矩阵P中对应的2行行向量近似.有损失函数:

(14)

本文利用Belkin等人[32]的方法来求解式(14)，首先我们定义对角型矩阵D∈(n+m)×(n+m)，其元素Di i为矩阵W的第i行之和，即:

(15)

则将式(14)展开并经过一定的线性变换，得到:

ε(P)=2tr(PT(D-W)P).

(16)

因此,要使得ε(P)最小，则只需要找到一个矩阵P，使其满足PT(D-W)P的迹最小.为了使得最优化问题式(14)有解并且使得解空间的维度不低于c，我们对矩阵P进行限制:

PTDP=I.

(17)

经过上述讨论，聚类结果的评价矩阵P的求解转化为求解满足式(17)的矩阵P，使得PT(D-W)P的迹最小.根据文献[32]，这样的矩阵P应当是由矩阵D-W的前c个非0最小特征根对应的特征向量组成的.则可以根据(D-W)p=λDp求得矩阵D-W的广义特征根，其中p为广义特征根λ对应的广义特征向量.最后，将前c个非0最小特征根对应的特征向量组成的矩阵P即为所求.

得到用户和物品的评价分布矩阵后，再根据评价值的大小确定某个用户或者物品所属的分组.在本文的算法中，只要用户或者物品对某个分组持有正的评价值，则将该用户或者物品分配到该分组中去，这样便得到了最终的聚类结果.

2.5 推荐结果的生成

如图2所示，图2(a)表示非聚类的协同过滤算法生成推荐结果的流程，它直接将原始的用户评分矩阵通过协同过滤算法进行计算，得到用户对其他物品的预测评分从而进行推荐;而在基于聚类的协同过滤算法中，如图2(b)所示，首先利用聚类算法对原始的用户评分矩阵进行聚类，得到若干聚类分组，然后对每个聚类分组分别使用传统推荐方法得到在这些分组上的推荐结果，最后，将所有分组得到的推荐结果进行汇总即得到最终的推荐结果.在将各个分组上的推荐结果汇总的过程中，由于聚类算法允许1个用户或者物品属于多个分组，因此可能会存在1个用户与1个物品同时属于2个不同分组但是预测得分不同，本文的处理方式为选择用户评价得分较高分组上的预测得分作为最终结果.

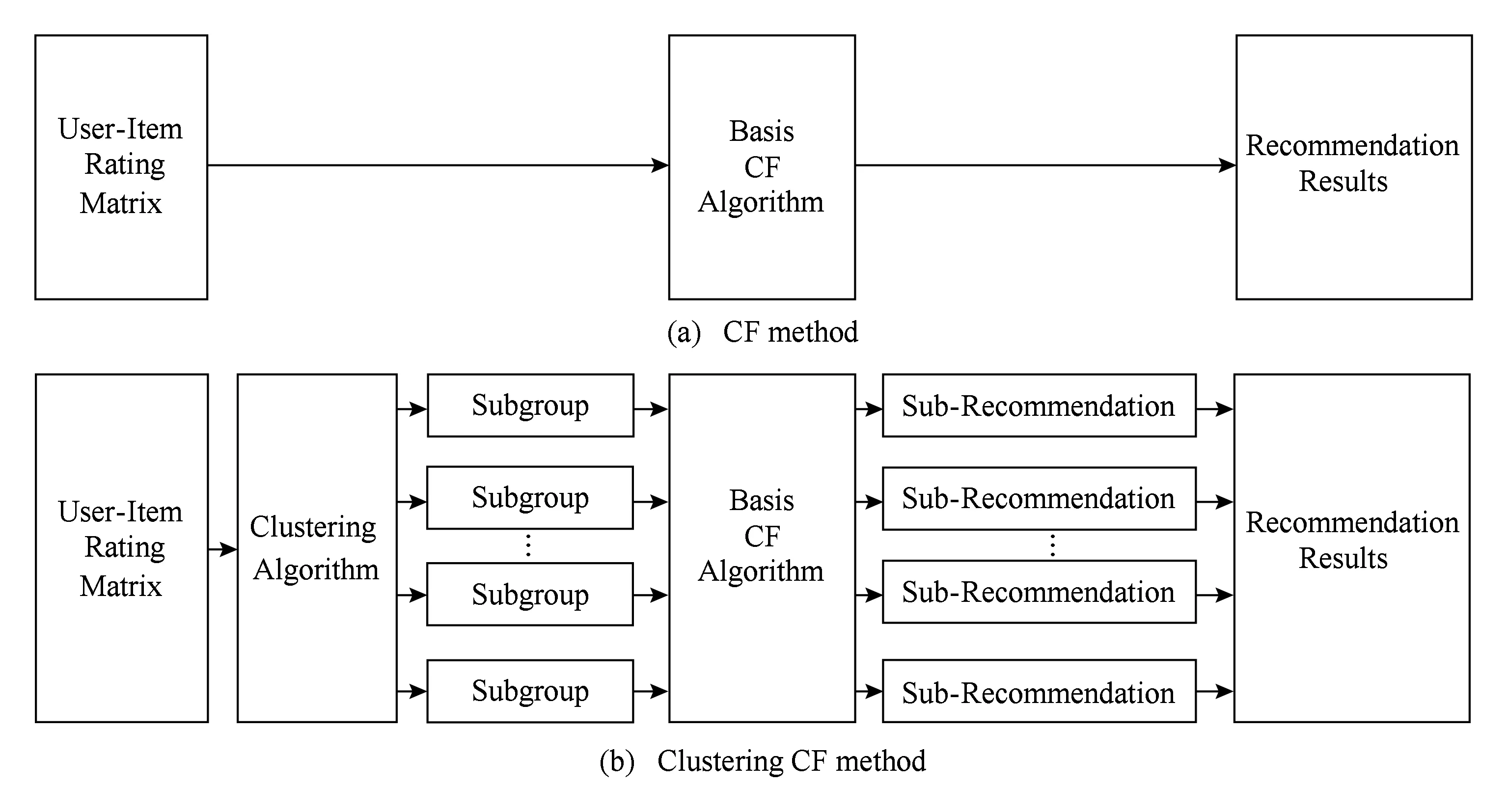
Fig. 2 The framework of the CF and clustering CF method图2 协同过滤算法与聚类的协同过滤算法的推荐框架

3 实验评估

3.1 数据集

本文的实验将使用3个公开数据集来检验聚类模型的性能:

1) MovieLens-100K

由于大部分推荐系统规模较小，这类系统的数据表现为数据少、用户平均打分数量中等，因此本文选用了MovieLens-100K数据集，它来自于MovieLens网站上的用户对电影的打分数据，包含943个用户对1 682部电影作品的近100 000条评分记录，用户的打分均为不大于5的正整数.

2) MovieLens-1M

部分推荐系统较为成熟，积累了一定的用户，但是物品品种类较为固定，因此此类推荐系统表现为用户量较多、商品数量较少、平均用户打分次数多.针对该系统的特点，本文选用了MovieLens-1M数据集，它与MovieLens-100K数据集来源相同，不同的是它更晚发布且拥有了更多的用户与更多的评分记录，它包含了6 040个用户对3 952部电影的1 000 209条评分数据，且每个用户都至少对20部电影进行了打分.

3) Epinions

某些推荐系统表现为用户量与商品量都是庞大的，但是却只有很少的评分记录，很难从中分析用户喜好，因此，本文选用了Epinions数据集，该数据集包含了22 166个用户对296 277个商品的打分信息，显然，它比前2个数据集要大得多，但是，该数据集有很多用户打分次数较少以及很多物品缺乏有价值的评分信息，因此，本文对该数据集进行了预处理，将打分次数低于10次的用户从数据集中移除，同样地，将被打分次数少于10次的商品也移除，最后，得到了21 109个用户对13 957件商品的433 507条评分数据.

这3个数据集的统计信息如表2所示.其中，Sparsity表示评分矩阵中空元素(未评分)所占的比例，即：

Table 2 The Statistics of the Three Datasets表2 3个数据集的统计信息

从表2可以看出,MovieLens-100K数据集规模最小;MovieLens-1M数据集平均用户打分次数最高，意味着信息更加丰富;而Epinions数据集最为稀疏，有着庞大的用户与物品量却拥有着较低的打分数量.

3.2 评估指标

在实验性能的评估上，本文分别从预测性能与推荐性能2个方面进行测试.

1) 在预测性能上.本文采用推荐系统领域内比较常用的平均绝对误差(mean absolute error,MAE)指标，其表达式为

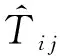
2) 在推荐性能上.本文采用TopK推荐方法，即从预测结果中选出预测评分最高的K个物品并排序，然后比较选出的这K个物品与测试集中用户最喜爱的K个物品的吻合程度.采用的评估指标为归一化折损累积增益(normalized discounted cumu-lative gain,NDCG)，对用户u，其对应NDCG计算为

其中,Nu表示测试集中用户u的评分数量，当模型推荐结果的第i个物品出现在测试集中用户的TopK列表中时，ri=1，否则ri=0.IDCG(ideal discounted cumulative gain)为常量，表示完美推荐时的累积增益，其表达式为

对所有用户的NDCG求平均值，即为最终的评估指标，显然，NDCG值越大，表示模型性能越好.

3.3 评估方法与对比算法

如图2(b)所示，利用本文算法进行推荐的过程是先将用户以及物品进行聚类，再在每个不同的聚类小组上调用其他协同过滤推荐算法得到推荐结果.因此，本文对比方法为采用不同的聚类算法进行分组，然后在各种算法得到的聚类分组上调用同一种协同过滤推荐算法来对比最终的预测性能和推荐性能.

在协同过滤推荐算法的选择上，本实验选择了当下较为主流的推荐系统所采用的算法，包括2个基于内存的协同过滤算法以及4个著名的基于模型的协同过滤算法:

1) Item-Based(IB)[7].其基本思想是预先根据所有用户的历史偏好数据计算物品之间的相似性，然后把与用户喜欢的物品相类似的物品推荐给用户.

2) User-Based(UB)[6].该算法与Item-Based算法类似，不同之处在于该算法计算的是用户之间的相似度.

3) SVD[14].该算法是基于SVD矩阵分解算法，将评分矩阵分解为多个矩阵的乘积，最后将利用这些矩阵的乘积预测用户的评分.

4) NMF[15].和SVD方法类似，不同的是它将原始评分矩阵分解为2个矩阵的乘积.

5) MMMF[16].该算法也是一种矩阵分解模型的算法，由于其具有较好的推荐性能而被广泛采用.

6) NPCA[17].该算法在文献[17]中被提出，它拥有着更高的预测准确度.

在聚类算法的选择上，本文采用4种算法来与本文方法进行对比:

1) UserClu(UC).它是单侧聚类算法，该算法基本思想是利用k-means算法对数据集进行基于用户的聚类，将用户分成多个组.

2) ItemClu(IC).该算法与UserClu算法类似，不同之处在于该算法是利用k-means算法对物品进行聚类.

3) CoClust(CoC)[29].它是双侧协同聚类算法，其思想是将用户与物品进行联合聚类，但是1个用户或者1个物品只能属于1个分组.

4) MCoC[30].它是双侧多类协同聚类算法，它和CoClust算法思想一致，不同之处在于该算法允许1个物品或者用户属于多个分组，这一点与本文的算法一致，这也更符合现实情况:1个用户可能对多个领域感兴趣.

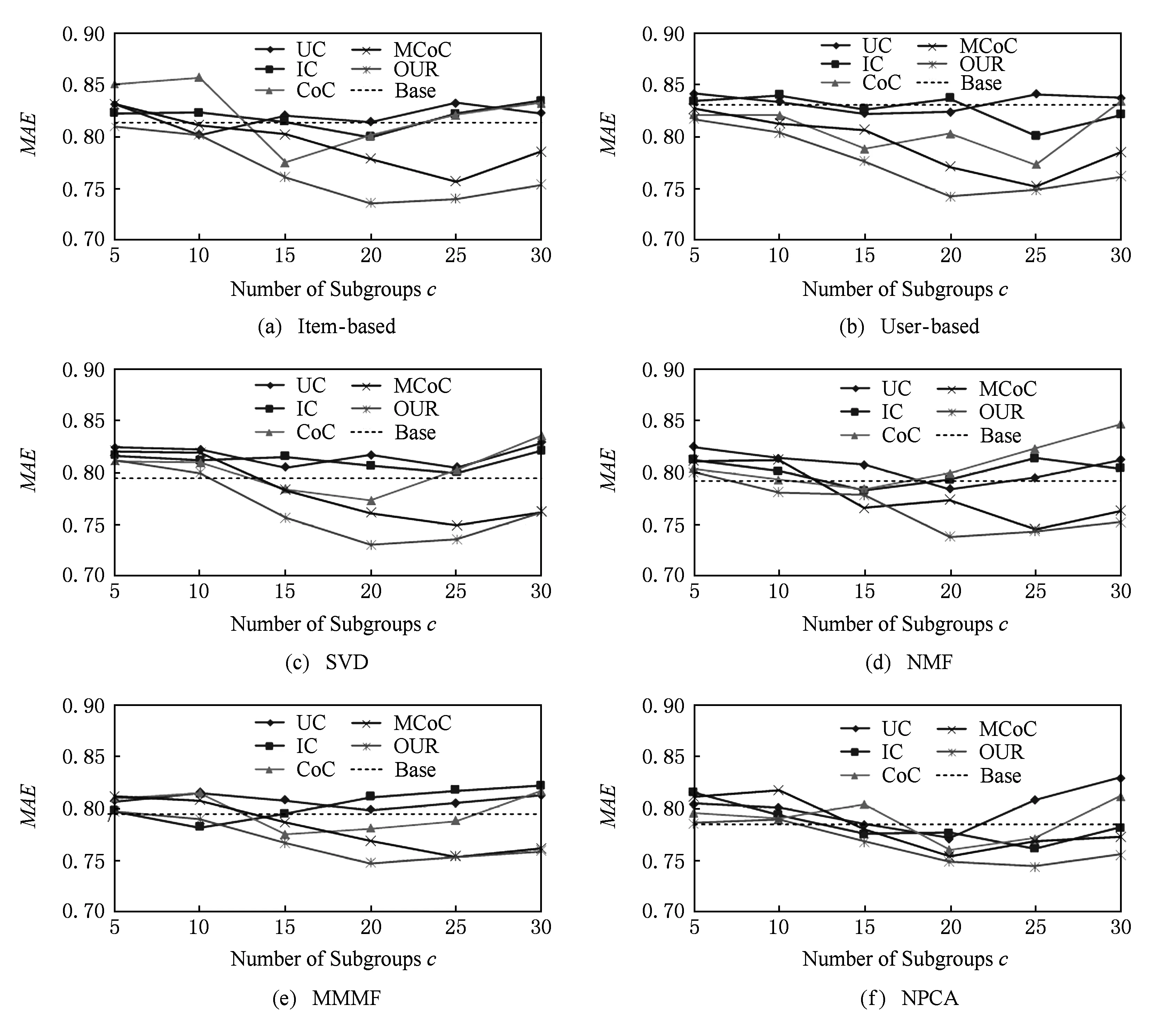
Fig. 3 The evaluation result of the prediction performance on MovieLens-100K图3 在MovieLens-100K数据集上的预测性能测试结果

3.4 参数设置

在进行实验之前，需要对本文模型有关参数进行设置.

1) 在特征提取阶段.用户特征维度a和物品特征维度b与具体的数据集有关，在MovieLens-100K数据集中，我们设置a=16，b=18；在MovieLens-1M数据集中，我们设置a=20，b=18；在Epinions数据集中，我们设置a=24，b=22；在学习率的设置上，在3个数据集中均为η=0.01.

2) 在图模型构建阶段.参数τ=1.5，由于3个数据集的评分制度都是1～5分的整数，因此有评分制中值Tmed=3.参数α与β是为了均衡评分权重与相似度权重之间的差异，而且，不同数据集相似度取值情况也有所不同，在MovieLens-100K数据集中α=1.3，β=1.3；在MovieLens-1M数据集中α=1.1，β=1.2；在Epinions数据集中α=1.9，β=1.5.

3) 在聚类计算阶段.聚类分组个数c是实验中的控制因素，我们主要考查在不同分组下本文模型与其他算法性能优劣.

4) 在性能评估阶段.由于大部分推荐系统都采用的Top10推荐，因此，评测指标NDCG的K值在3个数据集上均取K=10.

关于上述参数的选择原因及其对模型性能的影响，本文将在3.7节进行讨论.

3.5 实验结果

在本文的实验中，我们将3个公开数据集都分成2部分，随机选取80%的数据作为训练数据，剩下的20%作为测试数据，用来检测算法的预测和推荐性能.测试方法为先固定分组的个数，然后利用上述4种聚类算法对训练数据集进行分组，然后对所有算法得到的分组结果中选用同一种协同过滤推荐算法进行预测或推荐，统计各个算法的MAE值与NDCG值.由于矩阵分解模型的结果与分解的维度有关，因此，实验中分别对SVD，NMF，MMMF，NPCA算法的分解维度进行了不同的设置并进行实验，在所有不同纬度下取得的性能中，记录最好的一个来作为与本文方法的对比结果.

1) 在数据集MovieLens-100K上的测试

由于MovieLens-100K数据集规模最小，因此分组不易过多，否则由于数据过度分散导致信息丢失严重.在参数设置方面，本文通过多个分组规模测试，选取了最优效果较为集中的分组区间(5～30组).

预测性能的测试结果如图3所示，6个子图分别表示了6种不同协同过滤算法下的测试结果，在每个子图中，我们对比了包括本文算法在内的5种聚类算法在不同分组个数情况下的预测性能，横轴表示分组个数，纵轴表示测试指标MAE值，每个子图中的水平虚线(基准线)表示了在不分组的情况下直接使用协同过滤算法得到的MAE值，也即使用图2(a)的方法得到的结果.

从图3中可以看出，当分组较少时，各不同聚类算法差别不太明显，但是随着分组个数的增多，本文算法的优势越来越突出，分组数为20左右时，除了NPCA算法以外，在其他算法上都表现出了明显的性能优势.验证了本文的算法能够很好地应对小规模的推荐系统，提升它们的预测性能.

在Top10推荐性能测试中，我们的实验结果如图4所示：

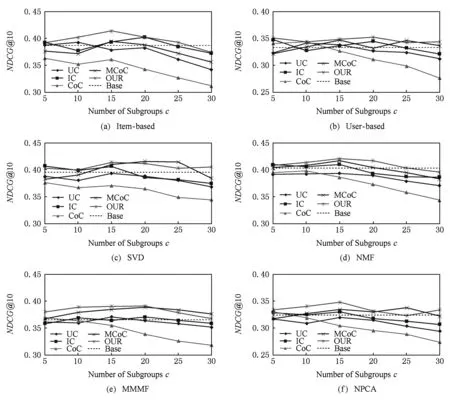
Fig. 4 The evaluation result of the Top10 recommendation performance on MovieLens-100K图4 在MovieLens-100K数据集上的Top10推荐性能测试结果

从实验结果可以看出，除了在图3(c)中推荐性能比MCoC稍差以外，本文聚类模型在其他算法的测试上均取得了较好的推荐性能.另外，对比图3与图4我们注意到，采用Item-based推荐算法虽然预测性能不高，但是推荐性能却比较好，相反采用NPCA推荐算法虽然取得了最高的预测性能，但是推荐效果却很差，经分析，我们认为出现这种“反常”现象的原因除了算法本身特点外，还包括数据集特点与推荐规则等原因.首先，分析表2可知MovieLens-100K数据集平均用户打分数量在106左右，则测试集中打分数约为20，这些评分中为5分的显然就更少了(不足10个)，因此，用户Top10列表中会包含很多低分物品，而我们的推荐规则只推荐高分物品，这导致用户列表中多数物品无法被推荐到，因此推荐性能取决于对测试集中仅有的若干高分物品的预测准确度，尽管NPCA算法MAE值较低，但是有可能其对高分物品的评估存在一定误差，从而导致预测性能好反而推荐效果不理想，另一方面，Item-based推荐效果好的原因，则是由于基于物品相似度的推荐往往符合用户的心理，相似的物品往往更容易引起用户注意，尽管Item-based方法会将原本低评分却与高评分物品相似的物品预测为高分并推荐(预测性能较差)，但该物品可能正好被用户因为与其喜欢的物品相似而购买或者关注(尽管用户购买后不喜欢)，因而在测试集高分物品不足的情况下，Item-based推荐算法可能会起到不错的效果.

尽管NDCG指标会出现上述“反常”现象，但仍然被众多推荐系统作为重要指标之一，因为它只关注算法对高分物品的预测准确度，而不必关心对低分物品是否也有准确的预测，这正是“推荐”所需要的.

2) 在数据集MovieLens-1M上的测试

MovieLens-1M数据集与MovieLens-100K数据源一致，区别在于前者数据规模更大，并且平均每个用户打分数与平均每个物品被打分次数在3个数据集里都是最高的.该测试用来检验本文算法在数据信息相对丰富的情况下的性能.我们在该数据集上做了同MovieLens-100K一致的实验，预测性能实验结果与Top10推荐性能实验结果分别如图5和图6所示.

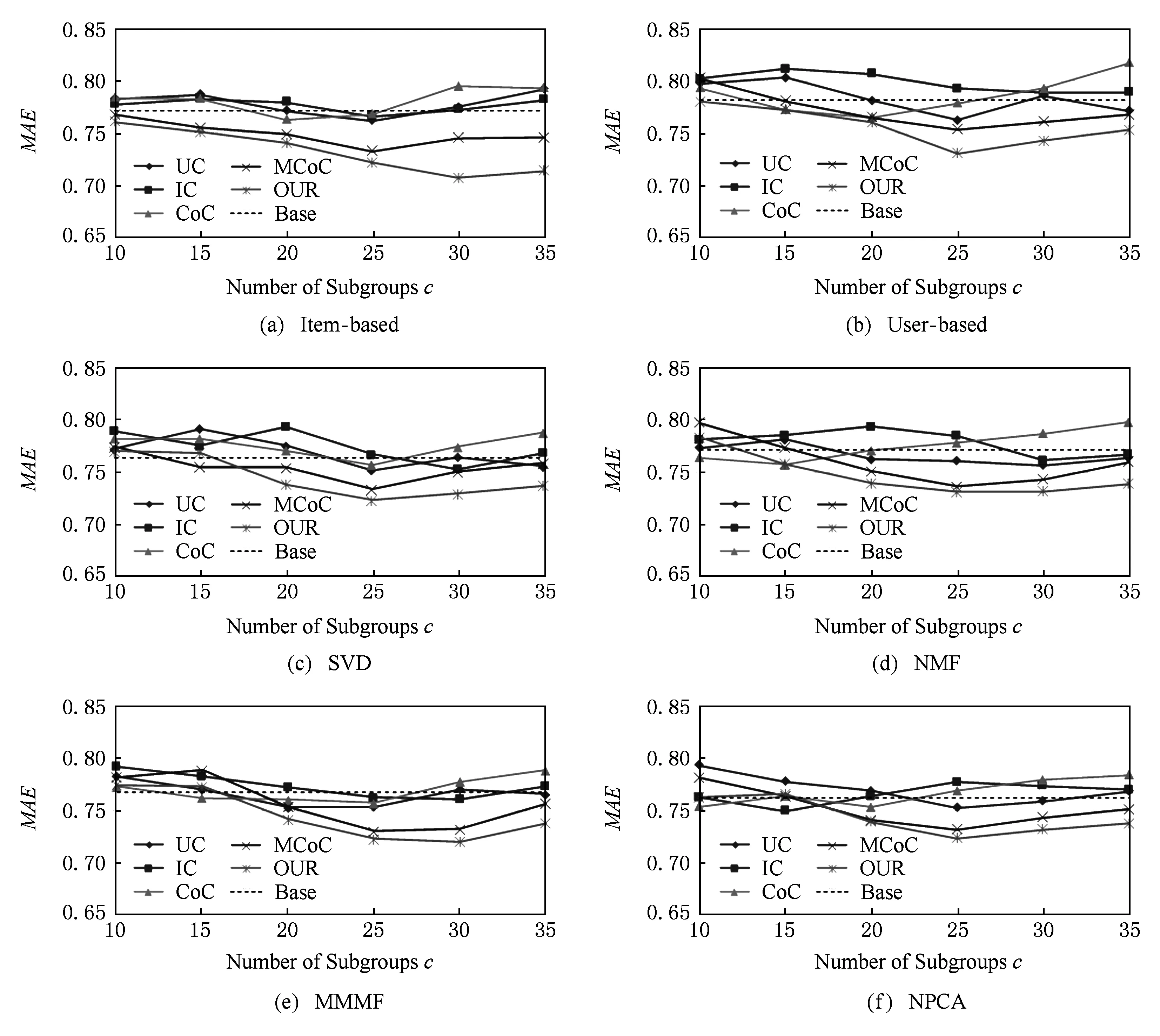
Fig. 5 The evaluation result of the prediction performance on MovieLens-1M图5 在MovieLens-1M数据集上的预测性能测试结果

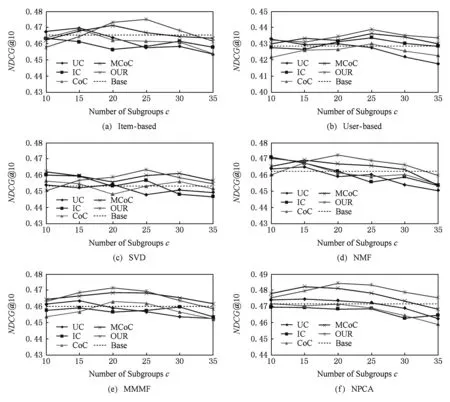
Fig. 6 The evaluation result of the Top10 recommendation performance on MovieLens-1M图6 在MovieLens-1M数据集上的Top10推荐性能测试结果

从图5实验结果可以看出，在数据集打分数量足够多的情况下，各个算法都表现出一定的稳定性，说明足够多的评分数能够帮助各聚类算法更加准确地捕捉用户和物品的特征，降低不同算法之间的差异.尽管如此，从实验结果来看本文算法所带来的预测性能提升与其他算法相比仍然是有优势的.另一方面，通过观察图6的推荐结果也证实了上述分析：与图4相比，图6中各算法的推荐性能差异也变得较小，波动幅度在0.03左右.但是本文模型以及MCoC与其他聚类模型相比仍然取得了微弱优势，另外，图6的实验结果也没有出现“反常”现象，正是由于测试集评分足够多，在用户的Top10列表中几乎都是高分物品，因此，预测性能越好一定程度上可以反映出推荐性能较好.

3) 在数据集Epinions上的测试

在所有3个数据集中，Epinions数据集规模最为庞大，该数据集稀疏率也是最高的，我们利用该数据集检验本文算法在应对大规模数据时的性能，实验结果如图7和图8所示.

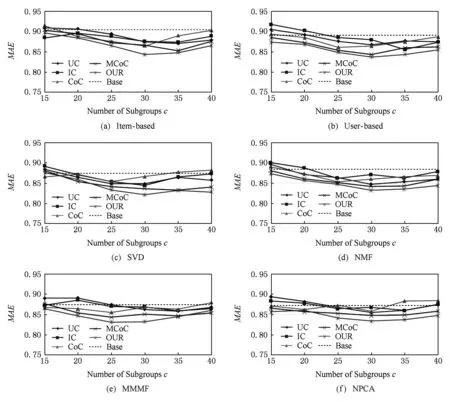
Fig. 7 The evaluation result of the prediction performance on Epinions图7 在Epinions数据集上的预测性能测试结果

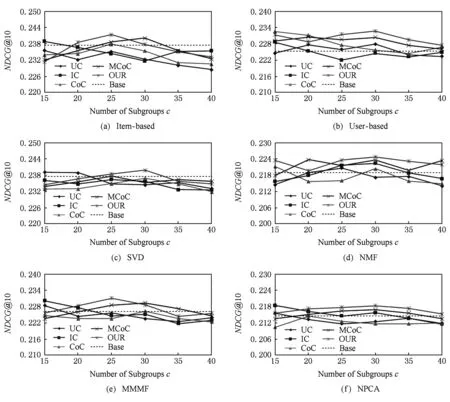
Fig. 8 The evaluation result of the Top10 recommendation performance on Epinions图8 在Epinions数据集上的Top10推荐性能测试结果

从图7的预测结果可以看出，大部分算法的预测结果MAE值都在0.85以上，和在MovieLens-1M数据集上的0.75相比性能大打折扣，说明该数据集大的稀疏性使得各个算法都难以捕捉用户物品的特征，预测准确度降低，即使增大分组个数，能够发掘的有效信息也是有限的，无法大幅度提升准确度，但是本文的算法依然能够发掘比其他算法更多的信息，提升了更大的预测性能，在所有同类算法中表现优异.验证了本文算法也能够应对具有高稀疏性数据的推荐系统.

但是另一方面，观察图8可以发现，各个算法的NDCG指标都在0.20～0.25之间，随着分组个数增大多数算法的推荐性能呈现无规律波动，且波动幅度达到0.1左右，通过分析表2我们认为，造成这种情况的原因是由于该数据集用户评分太少，只有平均20个左右，因此测试集中用户评分的物品数往往只有一两个甚至没有，这使得所有算法都难以正确推荐出测试集中的物品，即使增大分组个数也不一定能够提升推荐性能.

3.6 实验结果的总结和分析

在3.1节所述的3个不同数据集上的实验中，从实验结果图3、图5、图7对比各个算法的预测性能可以得到6个结论:

1) 图3、图5以及图7中大部分实验结果都位于基准线下方，这表示通过聚类得到的推荐结果要比无聚类的要好，说明通过聚类的方式能够提升协同过滤算法的预测准确度.

2) 基于特征的协同聚类算法在所有3个数据集上都有杰出的表现，证明了该算法在预测功能上的有效性.

3) 在3个数据集上本文算法与MCoC同其他聚类算法如UC与IC等相比，有更好地表现.原因是数据集的高稀疏性使得仅仅使用k-means进行聚类不能够得到理想的结果，并且双侧聚类算法能够获得比单侧聚类更多的信息.

4) 虽然MCoC算法也能够提升不错的预测性能，但是从实验结果上来看，本文的算法总是比MCoC更好一些，说明加入用户之间以及物品之间的相似性联系比单纯的依赖用户对物品的打分进行聚类能够得到更好的结果，能够利用更多的数据本身带来的信息.

5) 当分组数较少时，所有聚类算法的性能差别不大，有的聚类后的性能要比不聚类的协同过滤算法还要差.这说明较少的分组不能够完全区分用户以及物品的特点，分类不够准确，当分组个数适当时，大部分聚类后的预测性能都有明显提升.

6) 分组不易过多，所有的实验中当分组过大时，在折线图中都表现出了上升的趋势，意味着继续增大分组个数可能会得到更差的结果.原因可能是分组数太多，导致数据过度分散，丢失了过多的数据之间的联系，因此导致性能下降.

另一方面，观察实验结果图4、图6以及图8对比各个算法的推荐性能，我们有得到3个结论：

1) 在MovieLens-100K数据集上，NDCG指标值大约在0.3～0.45之间；在MovieLens-1M上则提升至0.41～0.48之间；而在Epinions数据集上，则只有0.2～0.25.在通过观察表2的数据集统计信息后，我们认为数据集中用户的打分数量一定程度上影响各个算法的推荐性能，打分数量越少，TopK推荐时测试集包含的低分物品就会越多，而这些物品一般不会被推荐到，因此推荐性能就会变差，显然，评分数量越多，越有可能获得准确的推荐.

2) 尽管数据集的特征对模型推荐性能产生一定的影响，但是在3个数据集上本文模型都取得了不错的推荐效果，经本节分析，推荐性能很大程度上取决于对测试集中高分物品的预测准确度，而本文模型在聚类过程中，评分越高越有可能出现在一个聚类结果中，因此，本文模型对于高分物品的预测准确度有一定的保障，从实验结果也可以看出，正是由于该原因，MCoC算法也保持着高预测准确度以及高推荐准确度.

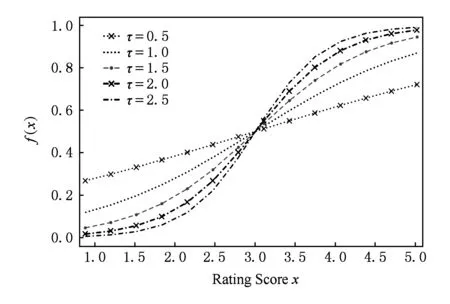
Fig. 9 The image of the mapping function with different τ value图9 不同τ值对应的映射函数图像

3) 在所有3个数据集上，本文模型取得最佳推荐性能时(NDCG值最大)在聚类结果上所用的推荐算法均为Item-based，说明在推荐性能上，Item-based算法最简单也最为有效，因为它总是推荐和用户兴趣相似的物品，但是由于该原因，导致Item-based算法的推荐结果缺乏多样性[29].

通过以上对预测性能与推荐性能的分析，我们可以认为，本文模型能够有效处理不同特点的推荐系统，提升它们的预测性能与推荐性能.

3.7 参数的影响

在本节，我们将讨论本文实验所采用3.4节参数设定的原因，主要讨论参数a，b，τ，α，β对模型性能的影响，以下涉及实验的部分均采用MAE指标.

首先分析参数τ，它是式(13)中的参数，该函数将评分映射成图模型中边的权重，我们分别选取不同的τ值来观察它将评分映射为权重的情况，如图9所示.从图9可以看出，当参数τ=1.5时，1～5分的映射权重比较合理，既弱化了高分间的差距，又不至于像τ=2.5时那样差距过小，当τ过小比如τ=0.5时，可以发现映射后的权值基本还是线性关系，没有起到弱化高分之间的差距的作用.

参数α与β是为了平衡图模型中上述函数映射的权重与基于相似度的权重之间的差异，当τ=1.5时，评分为5分时映射后的权重最大，为0.95，由于相似度的最大值可能大于0.95，也可能远小于0.95，因此需要用α与β去平衡这种差异.

参数α对模型性能的影响情况如表3所示，除了α外，其他参数同3.4节相同，从表3我们可以看出，在MovieLens-100K数据集上，本模型在不同推荐算法下取得最佳性能的α约为1.3，在MovieLens-1M数据集上取得最佳性能的α约为1.1，而在Epinions数据集上就需要α达到1.9.在3个数据集上，MAE值都随着α的增大而呈现先降低后升高的趋势，说明α过小会降低用户相似度的重要性，而导致聚类效果变差;如果α过大时，聚类主要取决于用户相似度了，因此模型退化为基于用户的聚类模型.同理可以分析，当β过大时，模型就退化为基于物品的单侧聚类模型，而表4的实验结果也证实了这一分析，观察表4可以发现，取得最好性能时的β值与我们3.4节所设置的一致.

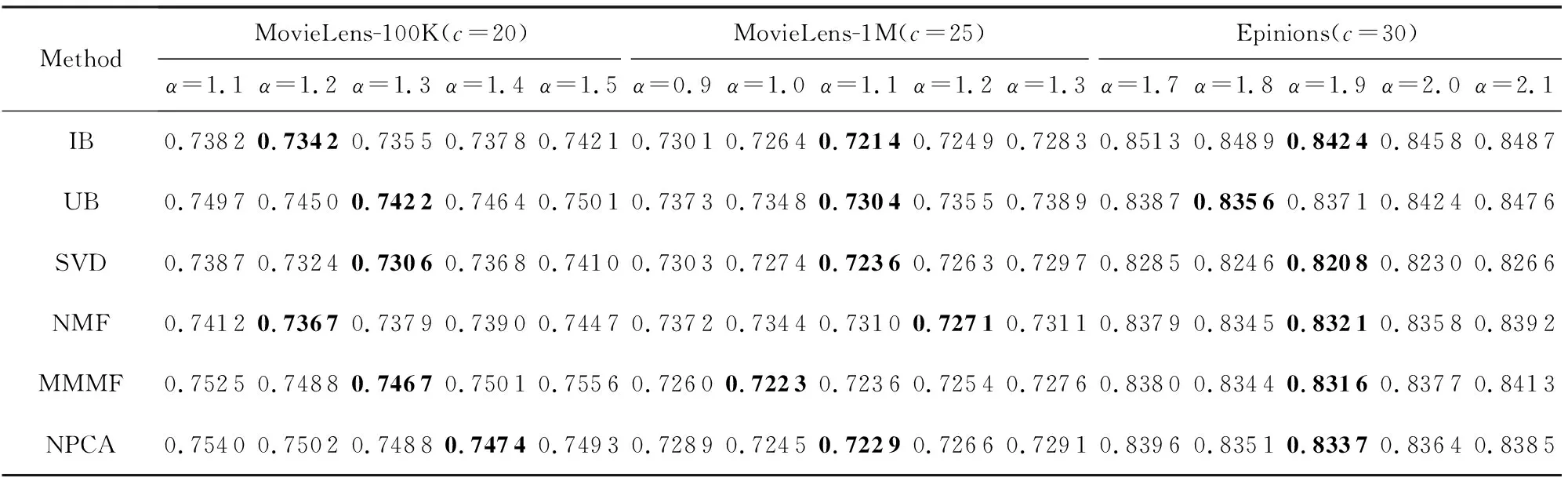
Table 3 Comparison of MAE Results with Different α on Three Datasets表3 不同α值在3个数据集上的MAE

Note: The best experimental results by setting differentαvalues under the same data set and recommendation algorithm are in bold.

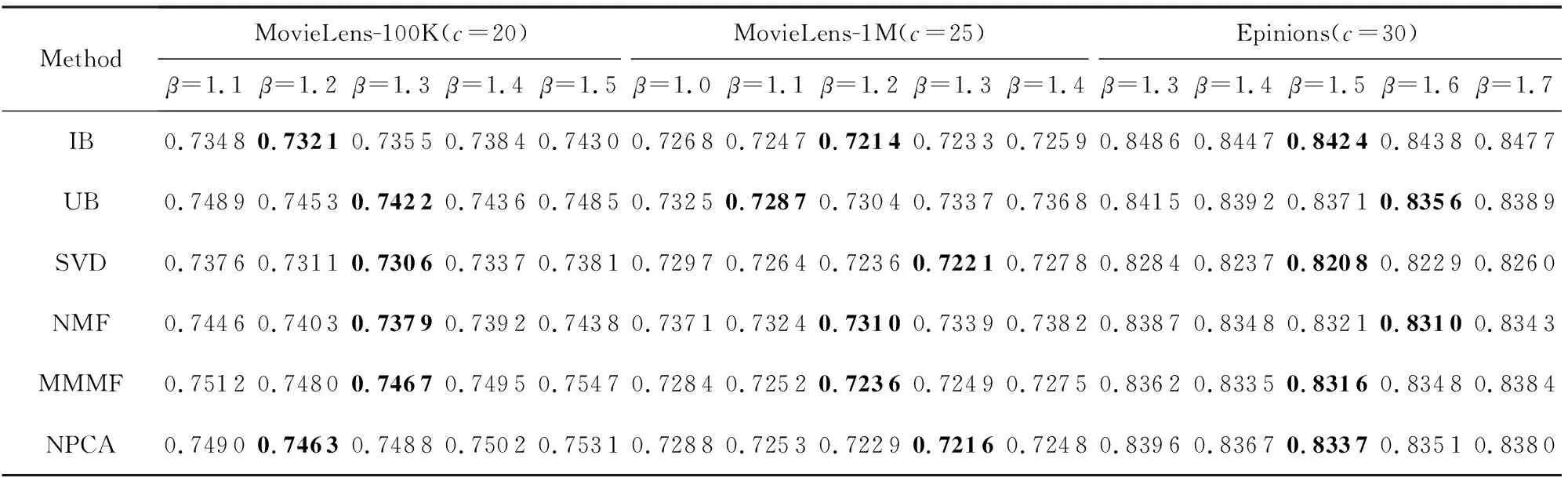
Table 4 Comparison of MAE Results with Different β on Three Datasets表4 不同β值在3个数据集上的MAE结果对比

Note: The best experimental results by setting differentβvalues under the same data set and recommendation algorithm are in bold.

最后，我们简单讨论参数a和b对模型性能的影响，该参数控制着特征提取过程中用户特征与物品特征的维度，实验结果如表5和表6所示.可以看出，随着特征维度的增长，模型性能提升较快，直到达到最好性能，但是继续增大维度，MAE值就会缓慢上升.分析认为，当维度较低时，特征提取不完全，没有很好的区分度，导致相似度计算不准确；当维度较高时，有可能会出现过拟合现象，因此模型性能缓慢下降.从实验结果可以看出，取得最好性能时的特征维度正如3.4节所设置.

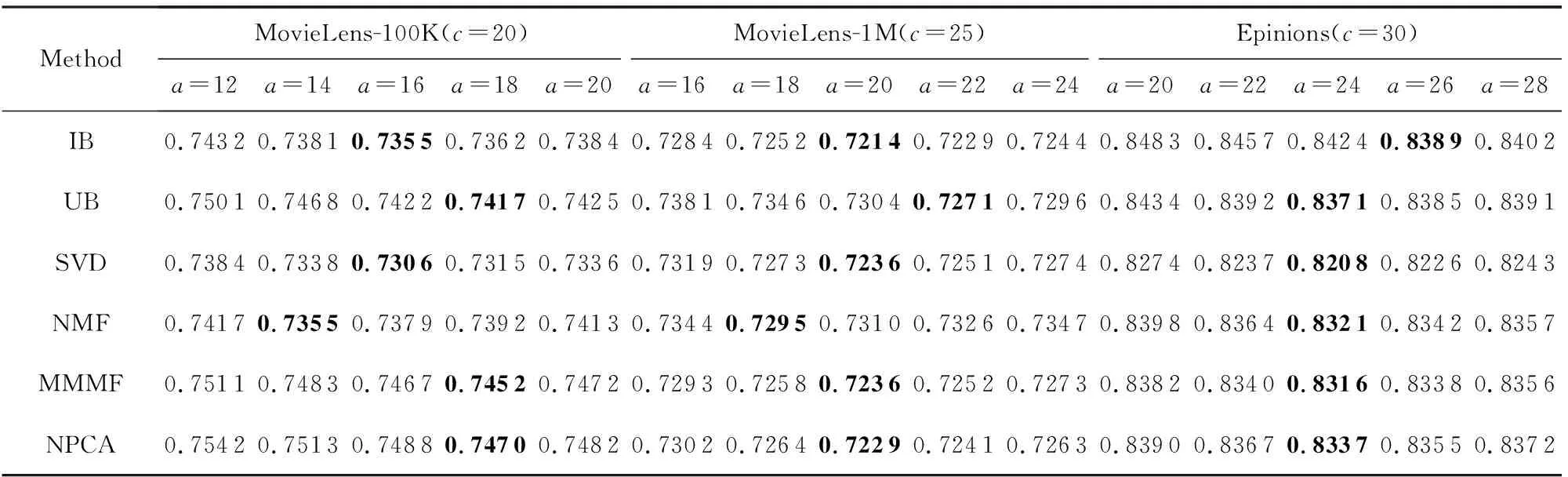
Table 5 Comparison of MAE Results with Different a on Three Datasets表5 不同a值在3个数据集上的MAE结果对比

Note: The best experimental results by setting differentavalues under the same data set and recommendation algorithm are in bold.

Table 6 Comparison of MAE Results with Different b on Three Datasets表6 不同b值在3个数据集上的MAE结果对比

Note: The best experimental results by setting differentbvalues under the same data set and recommendation algorithm are in bold.

4 总 结

本文提出了一种新的基于特征的协同聚类模型，它通过从用户评分信息中提取用户以及物品的特征，并将其应用在聚类过程中以提高聚类准确度，从而提高协同过滤算法的预测性能与推荐性能.本文模型首先通过二次回归模型发掘用户与物品的特征，然后通过一个图模型将用户物品的特征与用户对物品的评分等信息综合起来，从中计算出最终聚类结果.经过在3个真实的数据集上从预测性能与推荐性能2个方面来进行测试，实验结果有效地验证了本文模型的确能够更好地提升协同过滤算法的预测性能与推荐性能.在今后的工作中，我们考虑将这种从用户评分矩阵中发掘用户物品特点的方式进行拓展，添加一些其他信息来更准确地发掘用户和物品的特征，也能更进一步提升本文模型的性能.