教学主线统领 目标逐级落实——以《全等三角形复习》教学设计为例

杨丽娟

(昆山市葛江中学　215300)

数学课堂教学应以促进学生获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验为目标，增强学生分析问题和解决问题的能力，并以此为目标提高学生的数学素养[1].数学课堂教学，如果没有一以贯之的教学主线统领，就会导致教师的教学行为随意性大，学生负担沉重但学习效果差的现象.基于此，笔者2017年6月14日在苏州市首届“名师领航”高研班培训中开设公开课《全等三角形复习》，整个教学过程呈现两条教学主线：明线，即学习目标，通过复习全等三角形知识，掌握添辅助线构造全等三角形的方法，探索线段、角之间的数量关系；暗线，即教学目标，揭示添辅助线构造全等三角形的实质是实现图形的平移、旋转、翻折，培养学生数学表达能力，引导学生用掌握的知识解决问题.结合课堂教学，笔者思考的是在巩固知识的前提下，如何在有限的空间、时间和资源状态下，追求最大的教学收获.

1　利用简单问题唤醒认知储备，呈现知识系统

奥苏伯尔提出“学生已经知道了什么，再根据学生已经知道了什么进行教学”.这对我们了解学生、了解教学的起点，有的放矢进行教学是非常重要的.

复习课覆盖的“基础知识”，如果通过归纳成文或图表概括来梳理，会让学生感觉枯燥乏味，难以激发学习热情.所以精选简单的典型练习，通过问题呈现全等三角形的判定方法与性质，并通过针对性的讲解，增强知识点之间的融会贯通与理解.

1.1　设置开放性问题，在思维广度的延伸中梳理知识

思维的广度主要体现为思维主体善于根据整个问题从多角度、多方位来对问题进行思考.开放性问题可以给学生提供更广阔的活动空间和思维空间，使其思维富有弹性和流畅性，对启发学生的发散思维和培养学生的思维品质有着积极的促进作用.设置开放性问题，为学生在探索空间上作思维的开放预设，学生会因问题的开放而作“无拘无束”的思考，以流畅的思维保证知识梳理的全面性.

全等三角形的判定方法

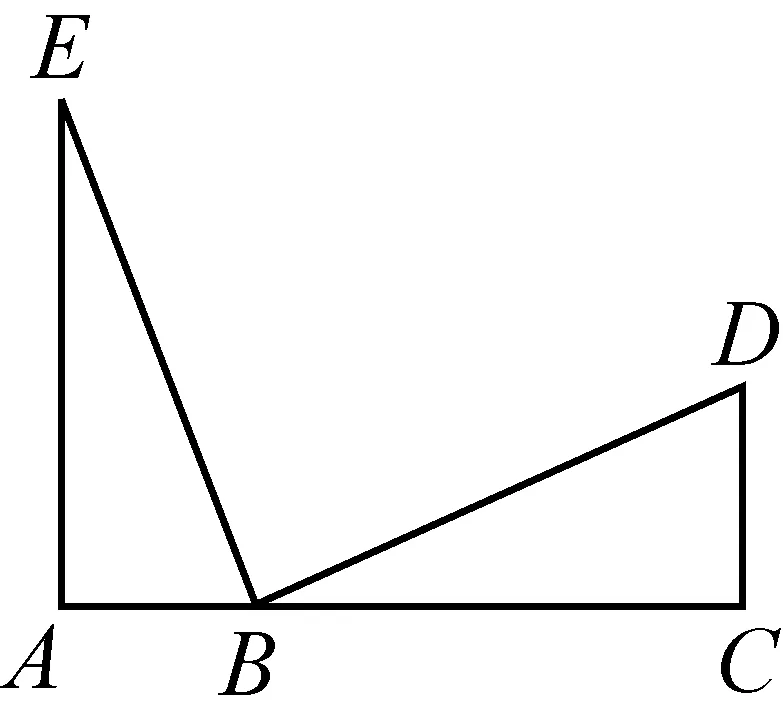
图1

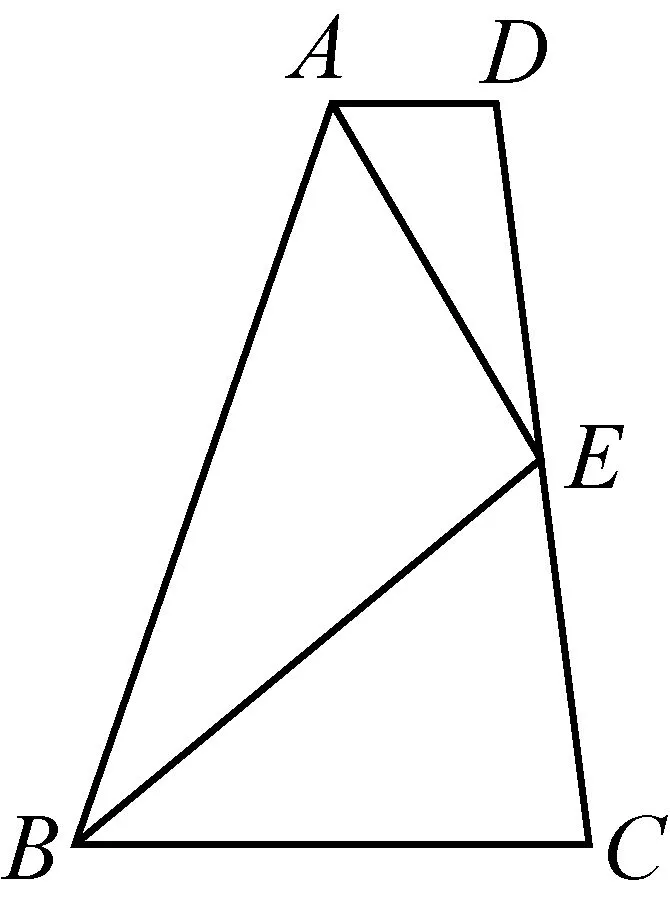
练习1如图1，A，B，C三点在同一条直线上，∠A=∠C=90°，AB=CD，请添加一个适当的条件，使得△EAB≌△BCD.

设计意图教材上介绍全等三角形的判定方法——1、两边及其夹角分别相等的两个三角形全等(SAS)；2、两角及其夹边分别相等的两个三角形全等(ASA)；3、两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS)；4、三边分别相等的两个三角形全等(SSS)；5、斜边和一条直角边分别相等的两个直角三角形全等(HL).本题若用“SAS”证明，可以添加条件“AE=BC”；若用“ASA”证明，可以添加条件“∠ABE=∠D”或“EB⊥BD”；若用“AAS”证明，可以添加条件“∠E=∠CBD”或“EB⊥BD”；若用“SSS”证明，需添加两个条件“AE=BC、BE=BD”(不符合本题要求)；若用“HL”证明，可以添加条件“BE=BD”.学生从不同的角度去观察图形、思考问题，用不同的判别方法解决问题，不仅有效再现学生的基础知识，更使学生的思维突破局限，给学生更多的思维空间，从而培养学生自主探究的思维品质.

1.2　通过简单练习，在思维深度的拓展中关注知识

思维的深度是指我们考虑问题时，要深入到客观事物的内部，抓住问题的关键、核心，进行由近到远、由表及里、层层递进、步步深入的思考.数学知识在各自的发展过程中，其纵向和横向都有着深刻的内在联系，通过简单练习寻找知识之间的联系，有利于学生从系统的高度思考问题，把握问题的实质.

全等三角形的性质

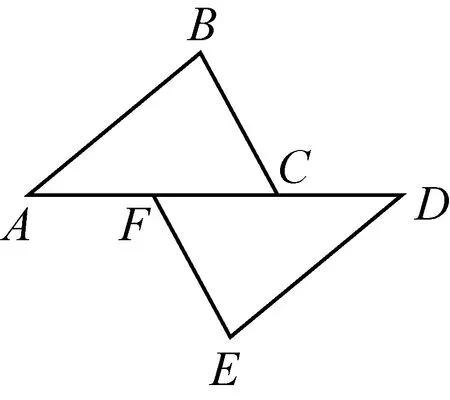
图2

练习2如图2，点A、F、C、D在同一条直线上，且△ABC≌△DEF.

(1) 若∠A=45°，∠B=100°，求∠DFE的度数；

(2) 观察图形，利用已知条件，你有什么发现？

设计意图第(1)小题，在△ABC中，根据“三角形内角和等于180°”得到∠ACB=35°，利用“全等三角形的对应角相等”得到∠DEF=∠ACB=35°.第(2)小题，结论众多：利用“全等三角形的对应边相等”可得AB=DE,、BC=EF、AC=DF，并在此基础上根据“等式性质”发现AF=CD；利用“全等三角形的对应角相等”除了可得∠ACB=∠DEF外，还可得到∠B=∠E、∠A=∠D，并在此基础上根据“内错角相等，两直线平行”发现BC∥EF、AB∥ED.练习中利用全等三角形获得对应量相等，这时可以引导学生归纳——要获得对应量相等，可以全等三角形为桥梁.

本题把知识放在系统中学习，不满足于停留在知识的表面和肤浅的理解，对知识进行综合梳理、寻找规律，发展思维的深度.

2　寻找基本图形归纳解题思路，实现数学应用

《义务教育数学课程标准(2011年版)》指出:在空间观念上，要求学生“能从复杂的图形中分解出基本图形，并能分析其中的基本元素及其关系”.在图形解题教学中，要引导学生主动识别提炼基本图形，并用基本图形寻找解题的思路，从而实现数学应用效益的最大化.

2.1　设计阶梯性问题，促进思维拾级而上

阶梯性问题是由简单到复杂、由浅入深、层层递进的数学问题串，满足不同层次的学生解决不同层次问题，激活学生不同层次的思维.设计阶梯性问题，低起点，高立意，学生可拾级而上，逐层深入地对题目进行探究，可以充分展示各自不同的探究思维深度.

例1已知正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上.

(1)如图3-1，连接DF、BF，证明：DF=BF；

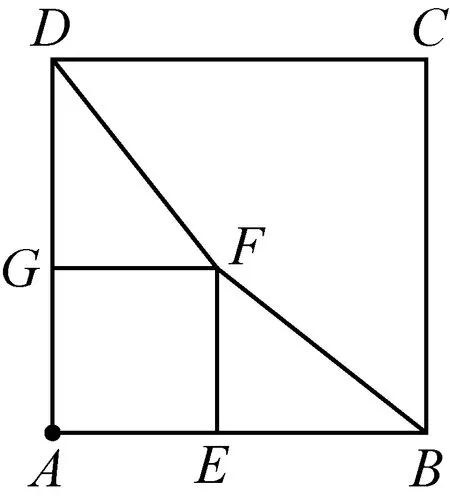
图3-1

图3-2

分析要证明DF=BF，这两条线段分别出现在△DGF和△BEF中，利用已知条件，发现△DGF≌△BEF(SAS)，借助全等三角形对应边相等，得到DF=BF.观察图形，整个图形关于AC成轴对称，故将△DGF沿AC翻折与△BEF重合，由此可知若含有轴对称图形，可用轴对称性质，沿对称轴翻折图形来寻找全等三角形.

(2)若将正方形AEFG绕点A顺时针方向旋转，在旋转的过程中线段DF与BF的长还相等吗？若相等，请证明；若不相等，连接DG，在旋转的过程中，你能否找到一条线段的长与线段DG的长始终相等．并以图3-2为例说明理由．

分析先利用几何画板演示，在旋转过程中，DF与BF随位置变化相等关系改变.连接BE，发现△ADG绕点A顺时针旋转90°与 △ABE重合，于是△ADG≌△ABE(SAS),可得DG=BE.由此可知，若出现有一个公共端点的相等线段AD=AB、AG=AE，可用旋转方法寻找全等三角形.

2.2　借助练习归纳模型，提升解题能力

对一些基本思路、基本方法和基本结论相同的问题进行模拟练习，通过练习对已经学过的知识进行整理，在这过程中打通学生的思维通道，提升他们分析问题和解决问题的能力.

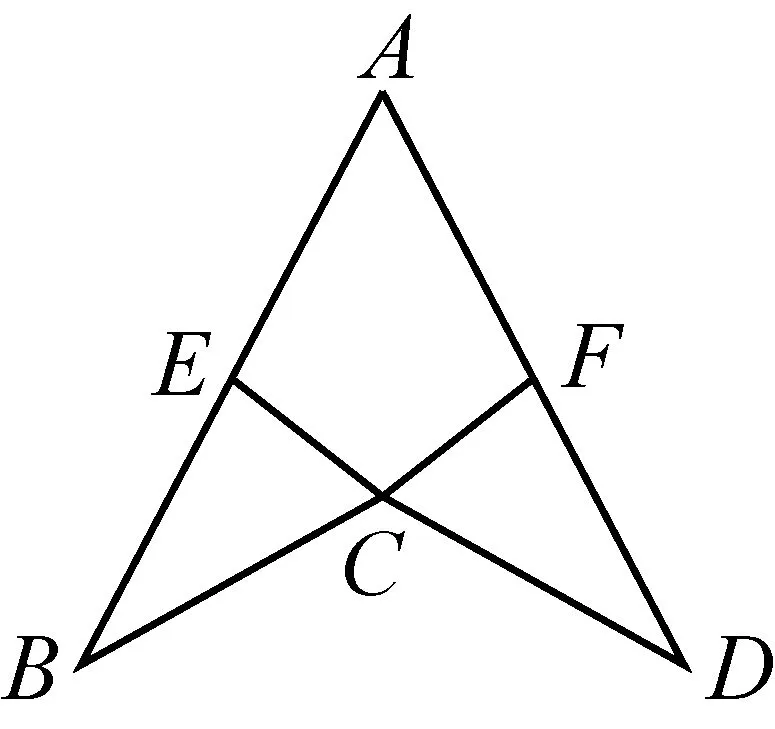
图4

练习3已知：如图4，AB=AD，CB=CD.

(1)求证：∠B= ∠D；

(2)若AE=AF，试猜想CE与CF的大小关系，并证明.

分析要证明∠B=∠D,图中没有现成的全等三角形可以利用,需添辅助线构造全等三角形.通过连接AC，其实质是将△ABC沿AC翻折与△ADC重合,由此构造全等三角形△ABC≌△ADC(SSS),得到∠B=∠D；在此基础上发现△AEC≌△AFC(SAS),得到CE=CF.学生独立思考后完成练习，深刻感受以添辅助线构造全等三角形为手段，实现图形的平移、翻折或旋转，获得对应量相等.

2.3　从相等关系到不等关系，抓住问题的本质

数学问题的本质是通过数学知识和方法承载的数学思考揭示解决问题的方法，为学生提供体会数学思考问题的方式，揭示数学问题内在的逻辑结构和本质关系，进而推动解题成果的扩大、解题模式的积累、解题经验的生成.

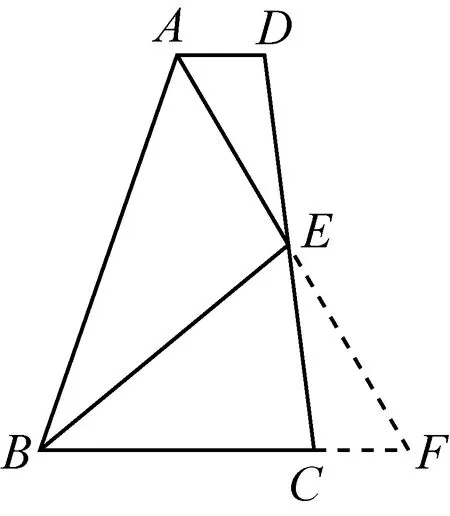
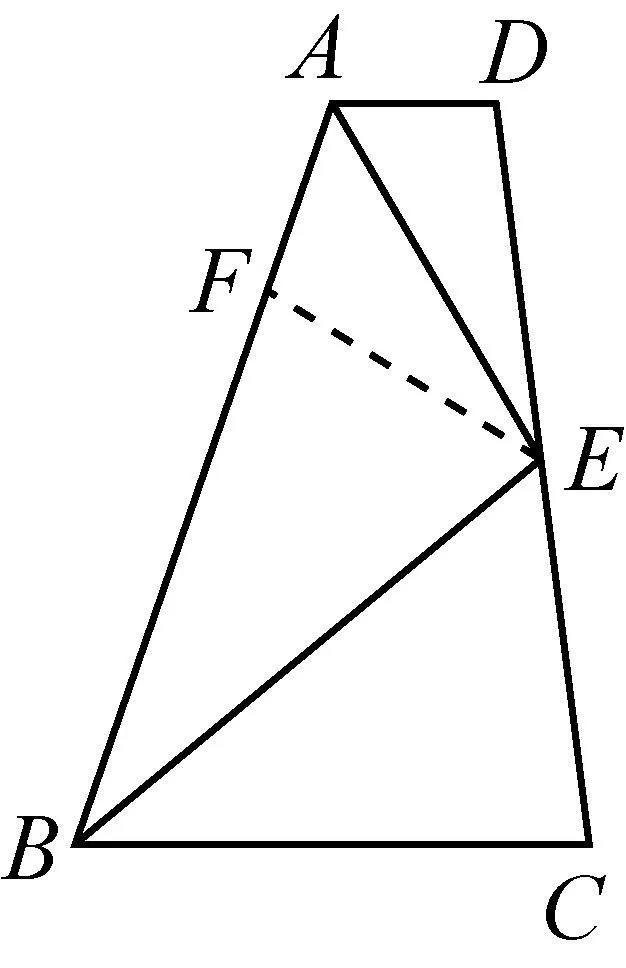
例2如图5-1，△ABC中，AD为BC边上的中线，求证：AB+AC>2AD.

分析要证明AB+AC>2AD，有两个关键:①创设2AD，②AB+AC>2AD形似“三角形两边之和大于第三边”，想办法将AB、AC、2AD转移到同一个三角形中.因此，如图5-2，延长AD到E，使DE=AD，连接CE，得△ABD≌△ECD(SAS)，于是AB=CE，在△ACE中，CE+AC>AE，即AB+AC>2AD.

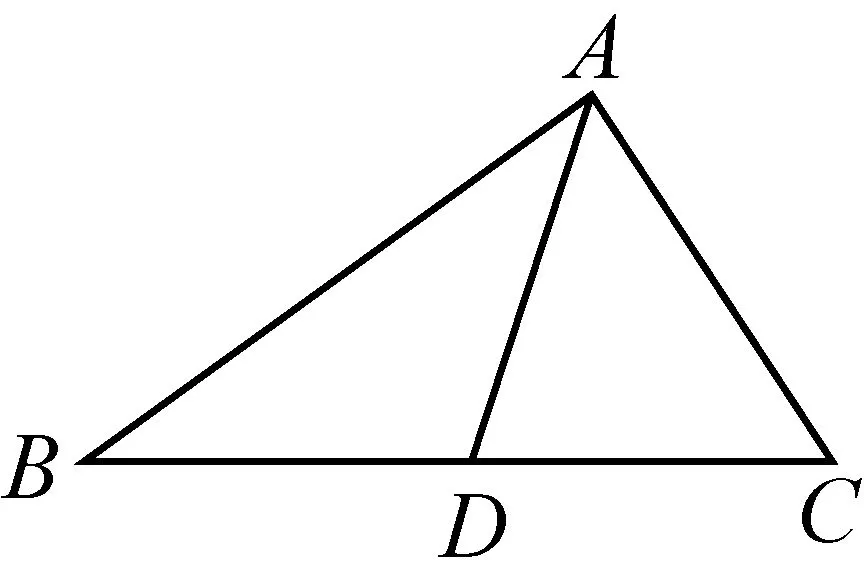
图5-1

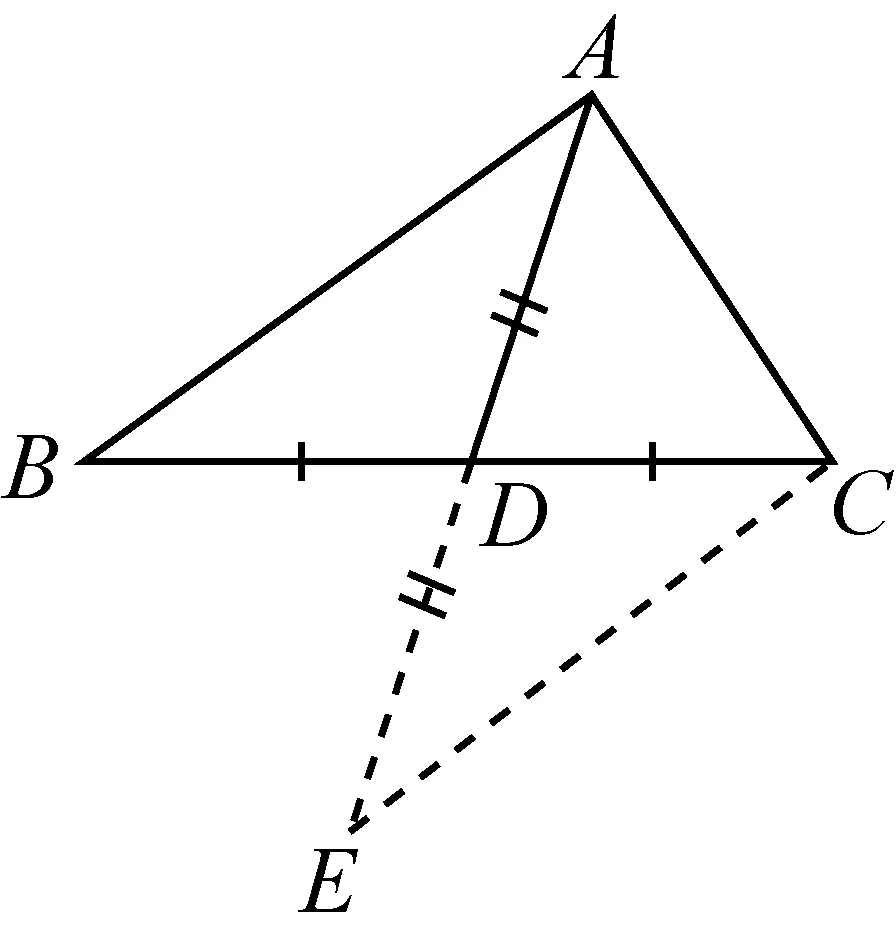
图5-2

变式若AB=5，AC=3，求AD的取值范围.

分析借助之前的解题思路，在△ACE中，利用三角形的三边关系可得EC-AC

设计意图学生习惯利用全等三角形获得对应量相等，本题要证明不等关系还是以全等三角形为桥梁.将△ABC的中线AD延长一倍，构造一对全等三角形，这种添辅助线的方法称为“倍长中线法”，其实质还是实现三角形的变换:若连接EC，是将△ABD绕点D旋转180°得到△CDE；若连接BE，是将△ACD绕点D旋转180°得到△BDE，以此抓住问题的本质.

3　构造基本图形探索数量关系，实现数学教育终极目标

数学教育的终极目标，不是仅仅掌握现有的专业知识，也不是单纯的为学生提供求解某些具体问题的工具，而是培养学生对理性(真理)的追求，造就一种精神，一种脚踏实地、不畏艰难的探索精神，善于抓住问题的根本，将复杂问题简单化，体现数学的智慧.

图6

例3如图6，四边形ABCD中，AD∥BC，EA,EB分别平分∠DAB,∠CBA,CD过点E.试探索AB、AD、BC之间的数量关系，并说明理由.

分析利用图中角平分线可以构成轴对称图形，学生根据之前介绍的翻折法，进行大胆猜想、小心证明,想到三种解题方法.

方法一如图7-1，延长AE、BC交于点F，发现△ABE沿BE翻折与△FBE重合，即△ABE≌△FBE(AAS)，得AB=BF、AE=EF；继而发现△ADE绕点E旋转180°与△FCE重合，即△ADE≌△FCE(ASA)，得AD=FC.因为BF=CF+BC，所以AB=AD+BC.

方法二延长BE、AD交于点F，解题思路同方法一.

方法三如图7-2，在AB上截取AF=AD,

图7-1

图7-2

连接EF.发现△ADE沿AE翻折与△AFE重合，即△ADE≌△AFE(SAS)，得∠D=∠AFE，因而∠C=∠BFE；继而发现△CBE沿BE翻折与△FBE重合，即△CBE≌△FBE(AAS)，得BC=BF；则AB=AF+BF=AD+BC.

设计意图本题探索得到一条线段等于两条线段的和，可以试用截长补短法，通过把一条长边截为两段，或延长短边使其等于所求边，其实质还是体现翻转、旋转，构造三角形全等.

变式如图6，四边形ABCD中，AB=AD+BC，EA,EB分别平分∠DAB,∠CBA,CD过点E.你能发现AD与BC的位置关系吗？请说明理由.

分析由已知条件AB=AD+BC，截长补短的指向明确，在例3的基础上，学生通过添辅助线，实现图形翻折、旋转，构造全等三角形，发现AD∥BC.

数学复习课是课堂教学的重要补充，有效的复习课教学直接关系到教育教学质量和学生数学能力的形成，是数学课堂教学的归宿.数学复习课的意义，在于通过对知识间本质联系的挖掘来加深学生对知识的理解和结构的重建，通过对题型类比的整理，来加强思维的渗透和方法的提炼.只有在知识、能力并重的同时，注意到数学文化的教育价值，才能真正将情感、态度、价值观落实到实处，把知识整理、题型归纳、思想渗透和方法提炼上升到应有的高度，在兼顾渗透探究意识和训练创新思维的同时，凸显学生数学综合素养的培养、延伸与发展.