日本中小学立体几何内容设置理念之个案评介
2018-07-16张晓雪
张晓雪 代 钦
(内蒙古师范大学数学科学学院 010022) (内蒙古师范大学科学技术史研究院 010022)
1 前言
立体几何内容是几何课程中的重要组成部分,它对学生数学思维的发展具有重要作用,在各国数学教科书中设置立体几何内容的顺序和程度不同.日本的小学、初中和高中均设置立体几何内容,同一个立体图形概念在小学、初中和高中由直观指出、操作实验到严格定义的螺旋方式上升,凸显其显著特点,这与我国中小学立体几何内容的设置有很大不同.
本文是对日本“数学学习指导要领”(相当于我国的数学课程标准)下的小学、初中和高中的立体几何内容设置的理念和特点进行阐述.立体几何在数学教学中扮演着不可或缺的角色,是培养学生空间想象力和逻辑思维能力的重要部分.此外,由于受地域差异或文化等影响,世界各国中小学的数学教科书中立体几何内容设置不尽相同,因此,研究其他国家立体几何内容设置对我国数学教科书的编写以及立体几何的教学具有一定的启示作用.
作为同受儒家文化影响的我国邻邦日本,各方面飞速发展,在世界各国备受瞩目.在近年来的TIMSS和PISA测试中,日本学生的成绩大多名列前茅,引人注目,这体现了他们数学教育的整体水平.日本现行的学制是“六三三制”,即小学六年,初中三年,高中三年.小学第一学年到第五学年每学年两册数学教科书,第六学年一册,共十一册;初中三年每学年一册,共三册;高中共五册,分别为《数学A》、《数学B》、《数学Ⅰ》、《数学Ⅱ》、《数学Ⅲ》,每册书的具体上课学期要根据“数学学习指导要领”相关规定和学校的实际情况来确定.
本文在介绍相关背景的基础上,结合日本东京书籍株式会社2015年发行的小学算数教科书、启林馆出版的2016年开始使用的初中数学教科书和2017年开始使用的高中数学教科书,以其中的立体几何内容为研究对象,从内容设置理念和个案分析两个方面来进行论述.
2 日本小学、中学立体几何内容设置
“数学学习指导要领”是日本编写中小学数学教科书的根据,小学、初中和高中数学学科总体目标“图形”教学要求分别概括为:(小学)通过数学活动,掌握数量和图形的基础的、基本的知识和技能,有条理地解决实际问题,培养表现能力的同时,使学生切实感受数学活动的快乐和用数学解决问题的益处,培养将数学运用于学习、生活的态度*曹一鸣.十三国数学课程标准评介(小学、初中卷)[M].北京:北京师范大学出版社,2012:180.;(初中)通过数学活动,加深对数量和图形的基本概念和原理、法则的理解,习得数学的表现和处理方法,提高数学性的思考表达能力的同时,切实感受数学活动的乐趣和数学的优越性,培养灵活运用数学思维、判断的态度*曹一鸣.十三国数学课程标准评介(小学、初中卷)[M].北京:北京师范大学出版社,2012:202.;(高中)要加深对空间中直线与平面的位置关系以及它们所形成的夹角的理解.另外,要理解与多面体相关的基本性质,并在考察事物过程中灵活应用*曹一鸣,代钦,王光明.十三国数学课程标准评介(高中卷)[M].北京:北京师范大学出版社,2013:145..根据该目标和结合学生的身心发展以及获得知识的认知规律,日本数学教育工作者们编写了小学、初中和高中三套数学教科书中的立体几何内容.
在《算数*1945年前日本将小学数学叫做“算术”,之后改为“算数”.1》(上下册)到《算数5》(上下册)和《算数6》中,有六册教科书中设置了立体几何内容,分别是《算数2》(下册)、《算数3》(下册)、《算数4》(下册)、《算数5》(上下册)、和《算数6》.在初中《数学1》、《数学2》、《数学3》三册中的《数学1》中设置了立体几何内容,在高中《数学Ⅰ》、《数学Ⅱ》、《数学Ⅲ》、《数学A》、《数学B》五册书中,除《数学Ⅱ》以外均设置了立体几何内容,下面列出小学、初中和高中数学教科书中立体几何内容的设置.
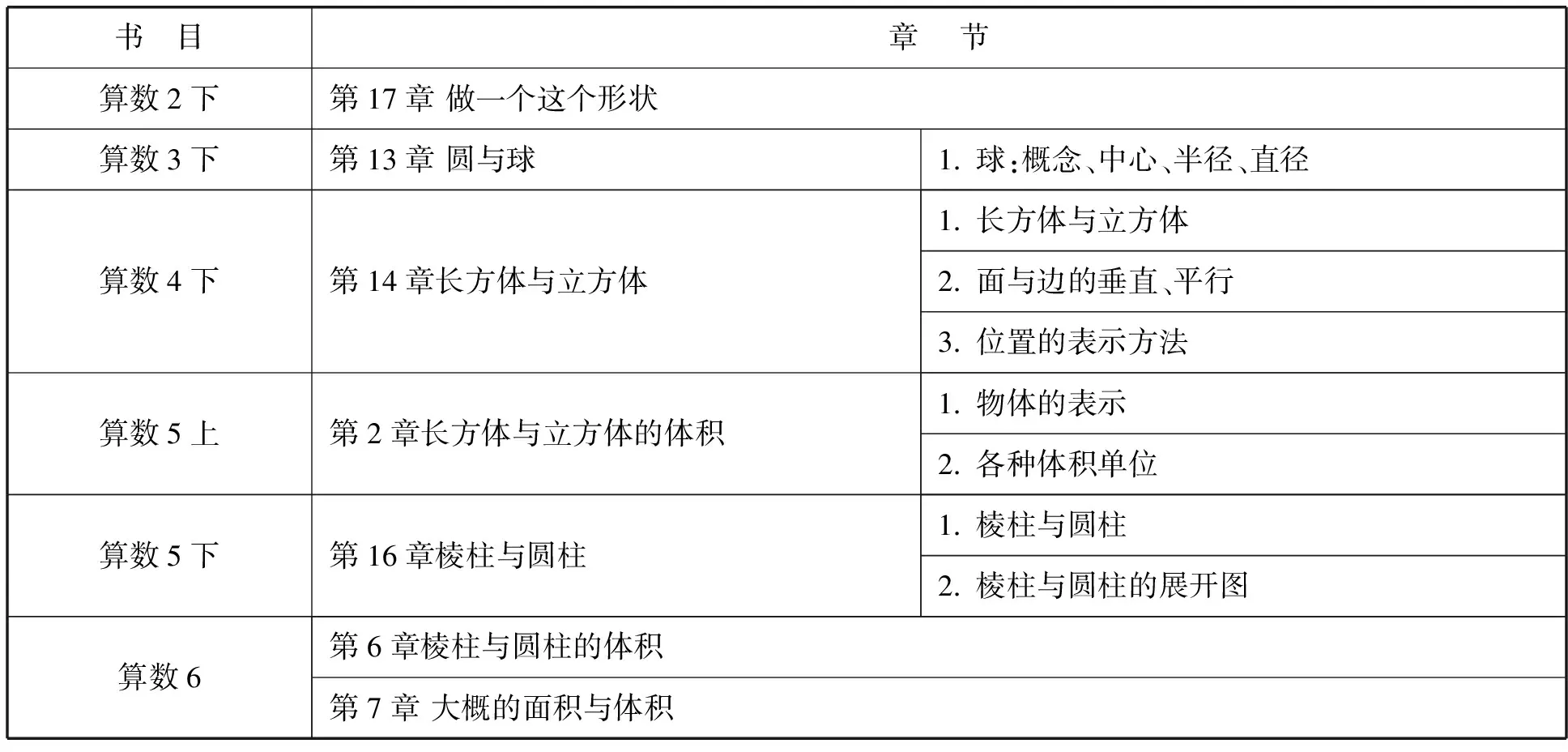
表1 小学立体几何内容设置
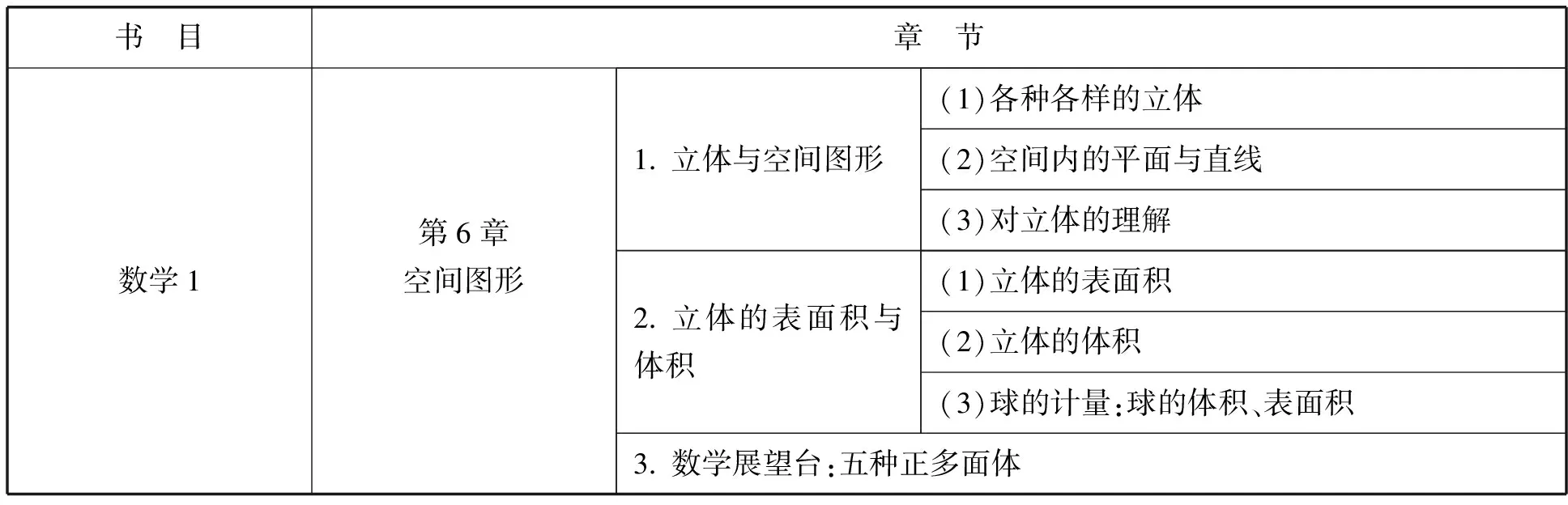
表2 初中立体几何内容设置
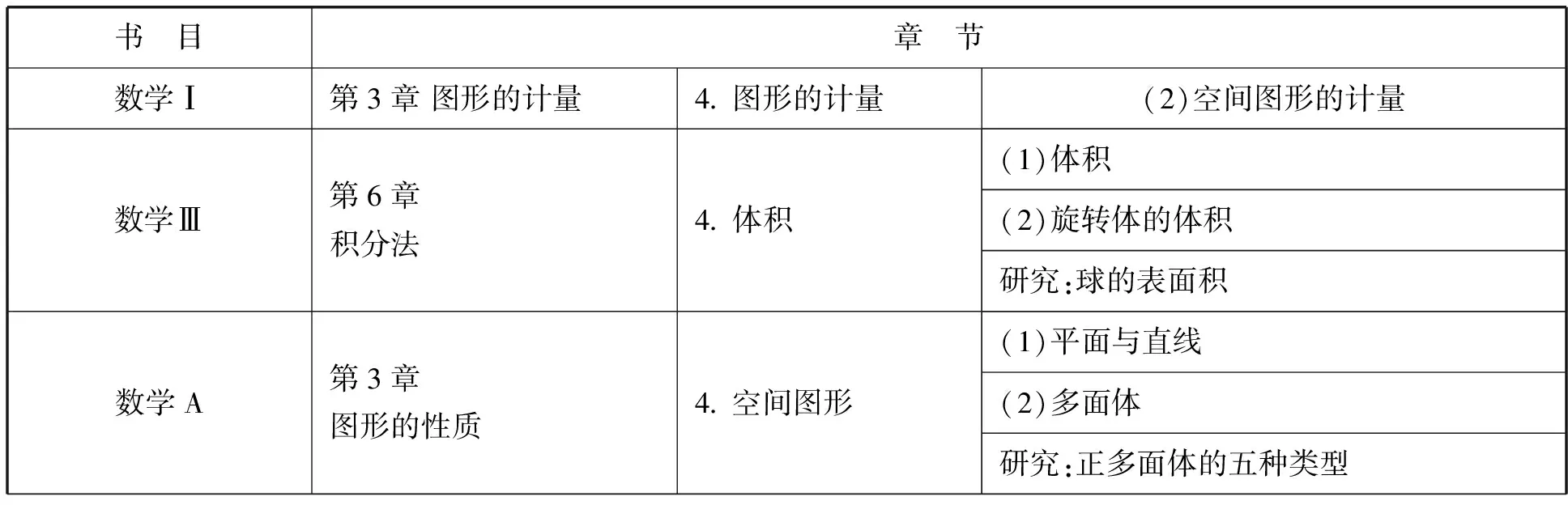
表3 高中立体几何内容设置

续表
从上表可见,日本从小学到高中是以螺旋形式来设置立体几何内容.日本在面临严峻社会问题的形势下,进行教育改革,对教科书进行改编,其中在对数学教科书中几何内容进行删减的情况下,仍保留了立体几何在小学到高中一定的课时量,可见日本对立体几何在数学教育中重视的程度之大.
小学立体几何主要是让学生通过数学活动,了解生活中简单的立体图形,这有助于小学生空间感觉和想象力的培养、表现自我以及更好地从生活角度理解数学,掌握数学.此外,在知识层面上可以让学生对立体图形有一个直观的、经验的认识,在学生的认知范围、接受能力之内进行立体几何的教学,也为中学立体几何的学习做好铺垫;初中的立体几何是让学生通过数学活动,从经验的积累中产生对立体几何图形的理解以及简单证明,是培养学生的思考力、判断力和表现力的一种实验几何;而高中的立体几何则是让学生通过数学活动,仔细地考察事物,培养其严谨的个性和创造性基础,是要经过逻辑推理、严格的理论证明得到的一种理论几何.
在以螺旋形式上升的立体几何内容中,虽然有重复的部分,但这些内容衔接着小学和初中,初中和高中,内容由浅入深,使它们之间的过渡更加自然,使进入新阶段的学生少一些陌生感和跳跃感,更加容易接受新的立体几何知识.并且包含解决问题的方法、传达的数学思想也对应着学生认知发展的规律,这有助于学生对新旧知识进行加工与重组,促进学生对立体几何的认识从具体化过渡到抽象化.
3 个案分析
个案1球
小学教科书中,在学习圆的知识之后对球的概念进行了简要介绍,给出“从哪个方向看都是圆的图形是球”直观描述的定义.如图1,并指出球从哪里进行切分,得到的切口都是圆,当球被切成一半的时候,这个切面圆是最大的,并且这个圆的圆心、半径、直径就是球的球心、半径、直径.
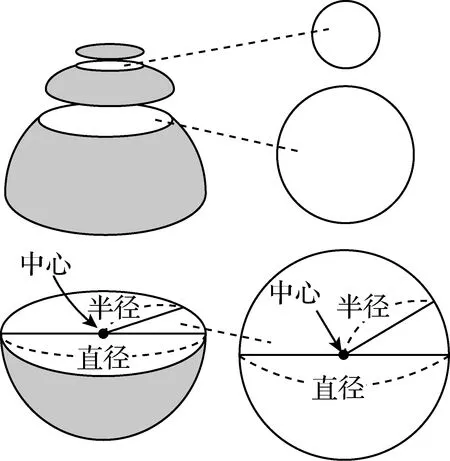
图1
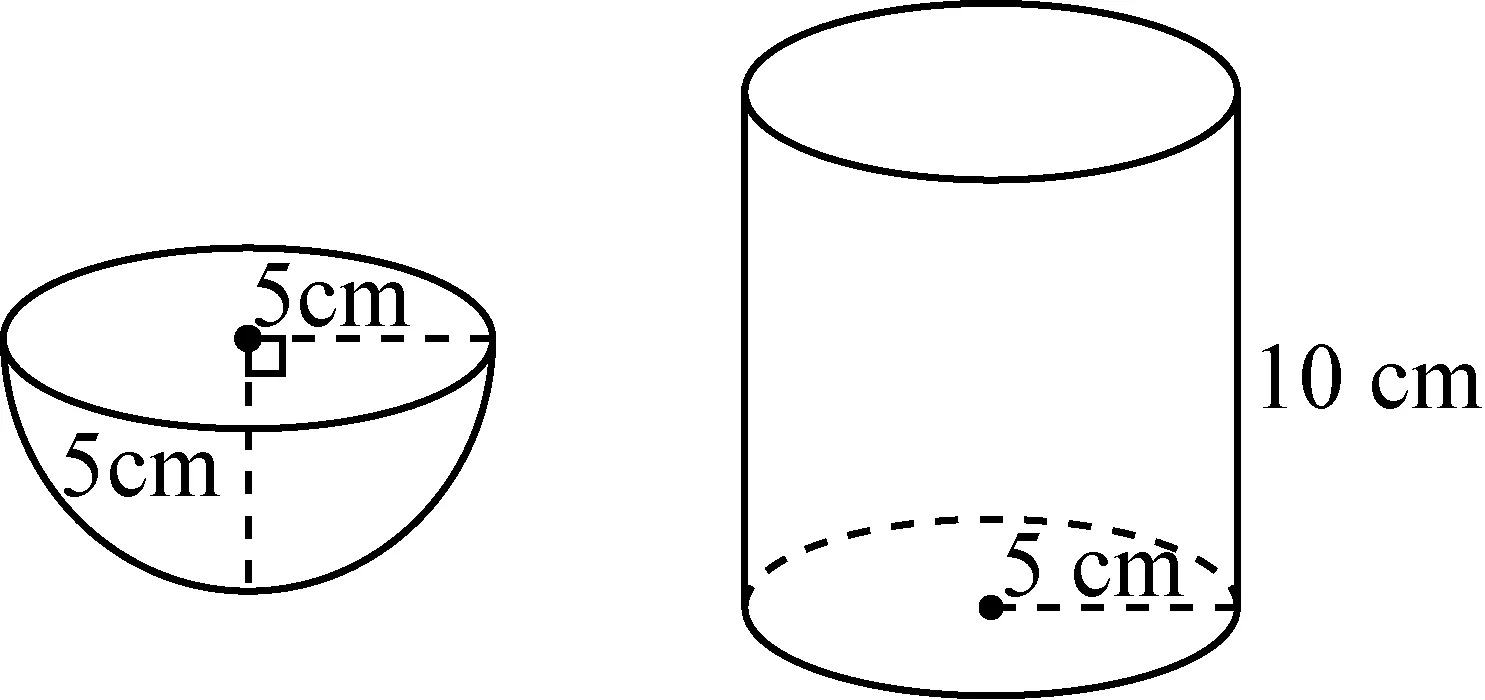
图2
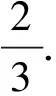
对于球的表面积S=4πr2则是直接给出的,但在思考题中提出如下问题:先给出一个半径为5 cm的半球,用毛线缠在半球的外侧,然后将2倍长度的毛线平置于平面上,形成半径为10 cm的圆,如图4,用球的表面积公式进行说明.这里采用实验几何的方法.
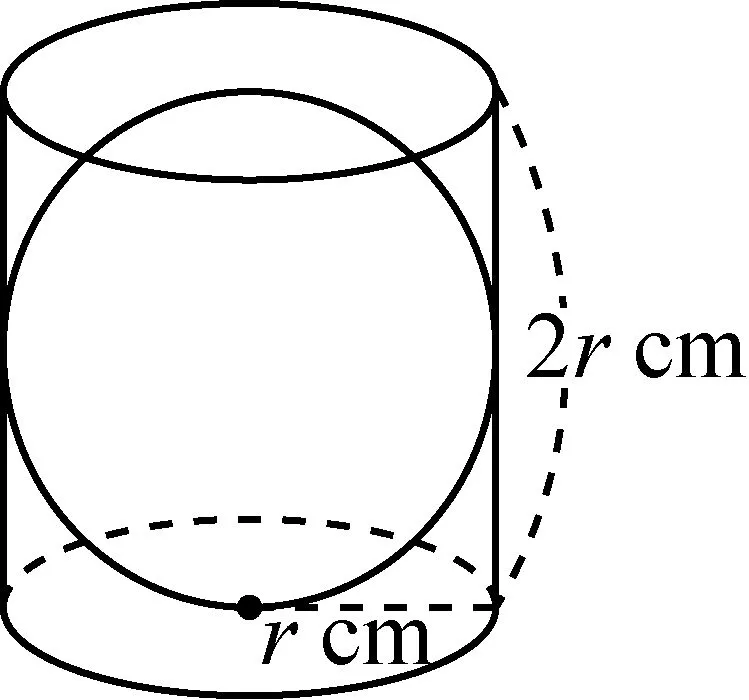
图3
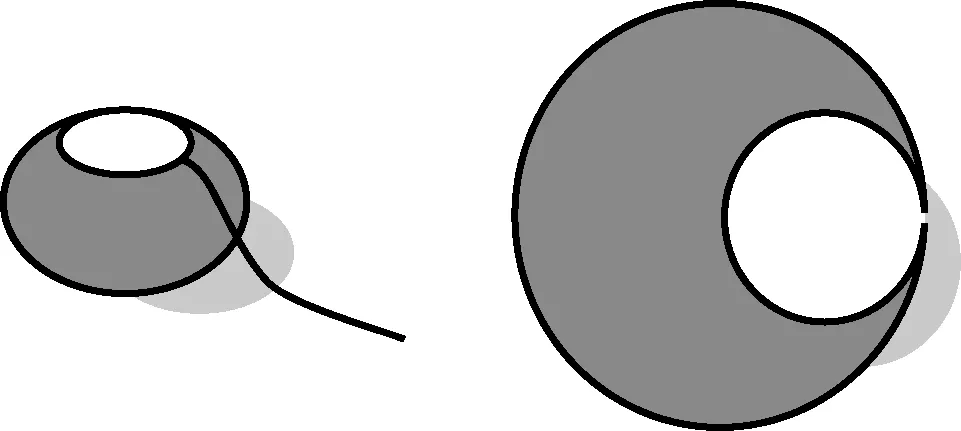
图4
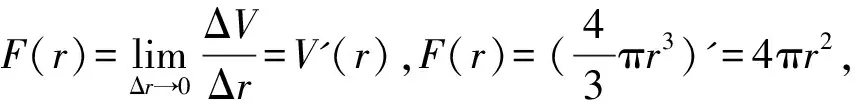
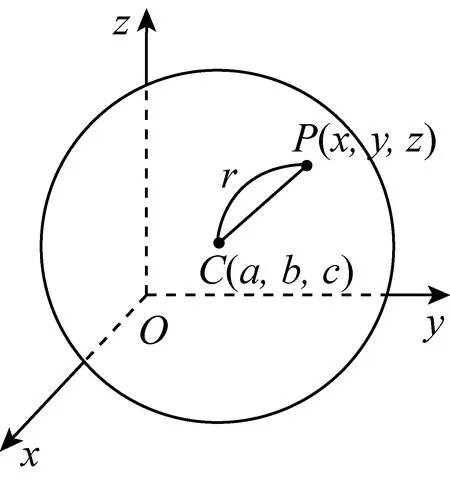
图5
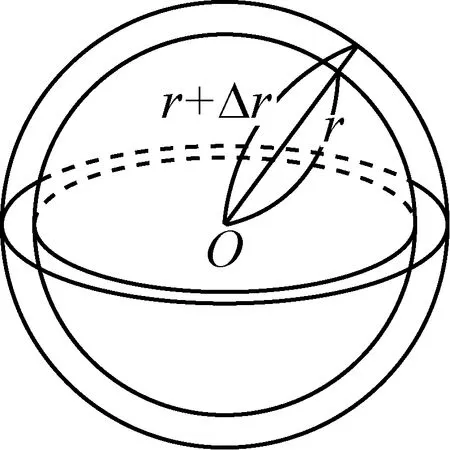
图6
这里十分清晰地交待了从小学球概念在视觉认知下的直观描述定义、初中球概念在经验认知下的实验性定义到高中球概念在理性认知下的严格定义,既考虑到学生的认知规律,又反映了数学学习的递进过程.
个案2直线与平面的垂直关系
“直线与平面垂直”这部分内容先后在小学、中学教科书中共出现了四次,具体过程如下:
第一次“直线与平面垂直”出现在小学《算数4》(下册),不过只是从长方体中进行了简要介绍,说明长方体的一棱与底面是垂直的,如图7,边BF与底面EFGH垂直.
第二次出现在初中《数学1》中,如图8,教科书在给出直线与平面的位置关系后给出直线与平面垂直:直线l与平面P交于点A,当直线l垂直于过点A平面P上的所有直线时,直线l与平面P垂直.这时,直线l就是平面P的垂线.直线l与平面P垂直的确定条件是:平面P上过交点A的两条直线分别与直线l垂直.
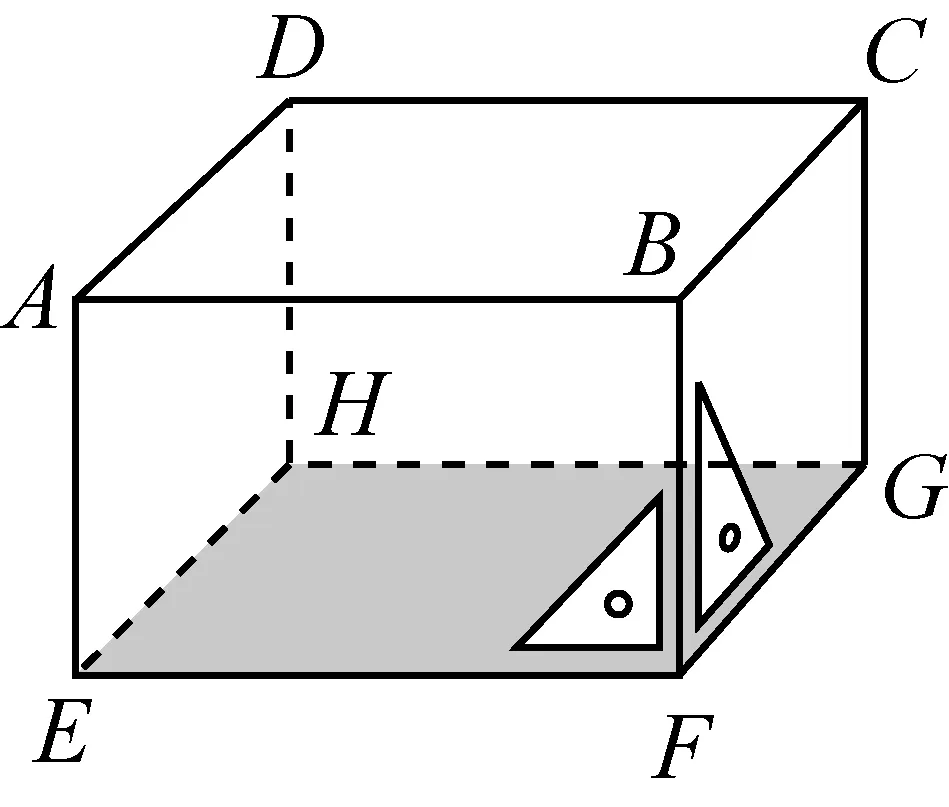
图7
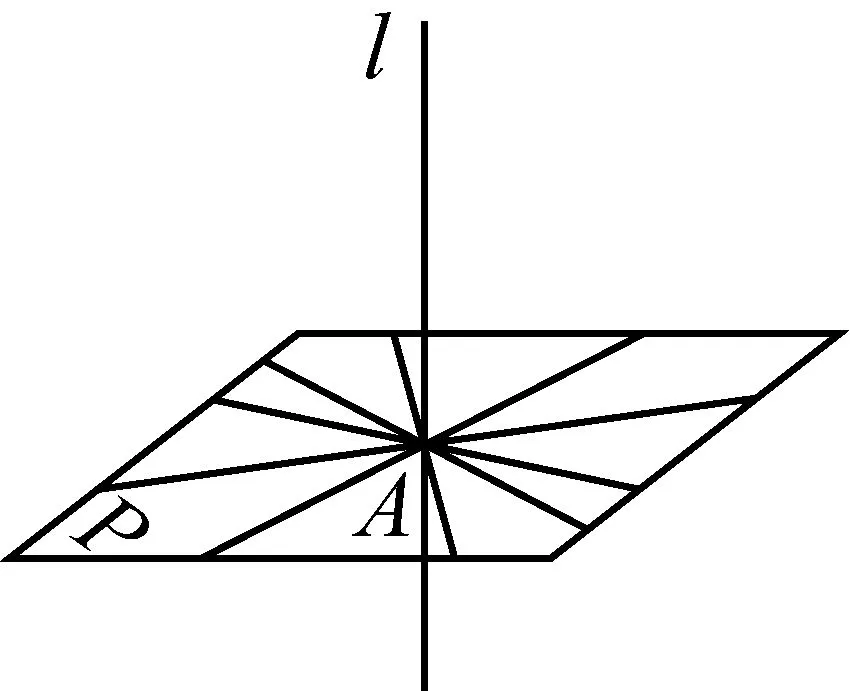
图8
第三次出现在高中《数学A》“空间平面与直线”中,如图9,同样是在直线与平面的位置关系后给出直线与平面垂直关系:当直线p与平面α交于点O时,若直线p垂直于过点O在平面α上引出的两条直线l,m,则p垂直于过点O的平面α的任意一条直线n.平面α上任意一条直线都与直线p垂直,则直线p就与平面α垂直,书写p⊥α.这时,p就是α的垂线.
第四次出现在《数学B》“空间向量”第一节中,如图10,平面α上任意一条直线都与直线p垂直,则直线p就与平面α垂直,书写p⊥α.若p与α上两条相交直线垂直,p就与α上所有直线都垂直,即p⊥α.
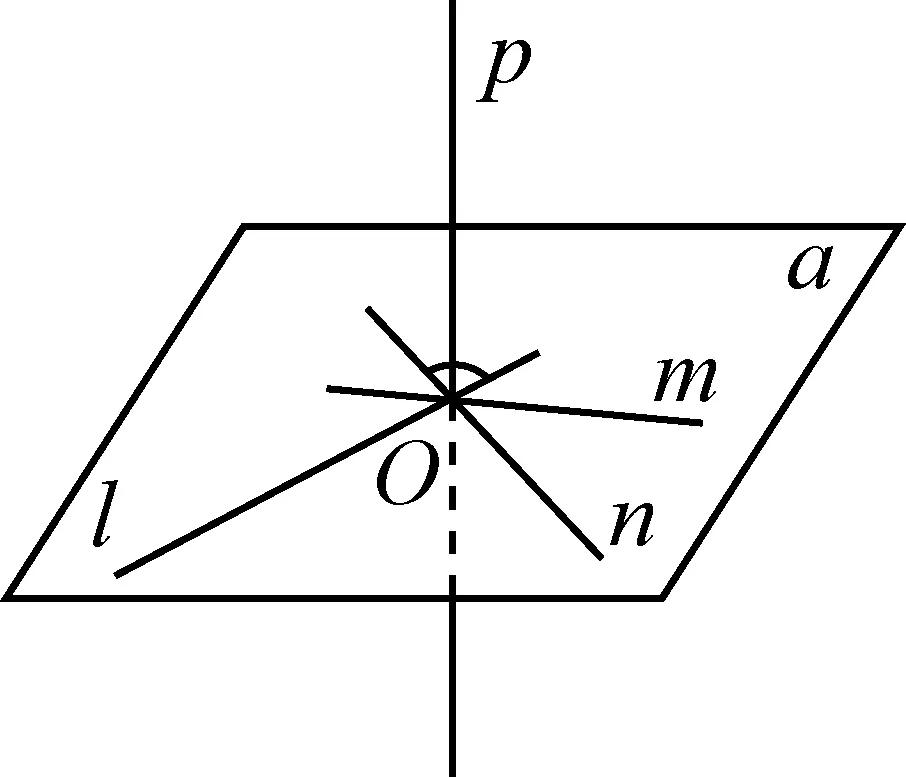
图9
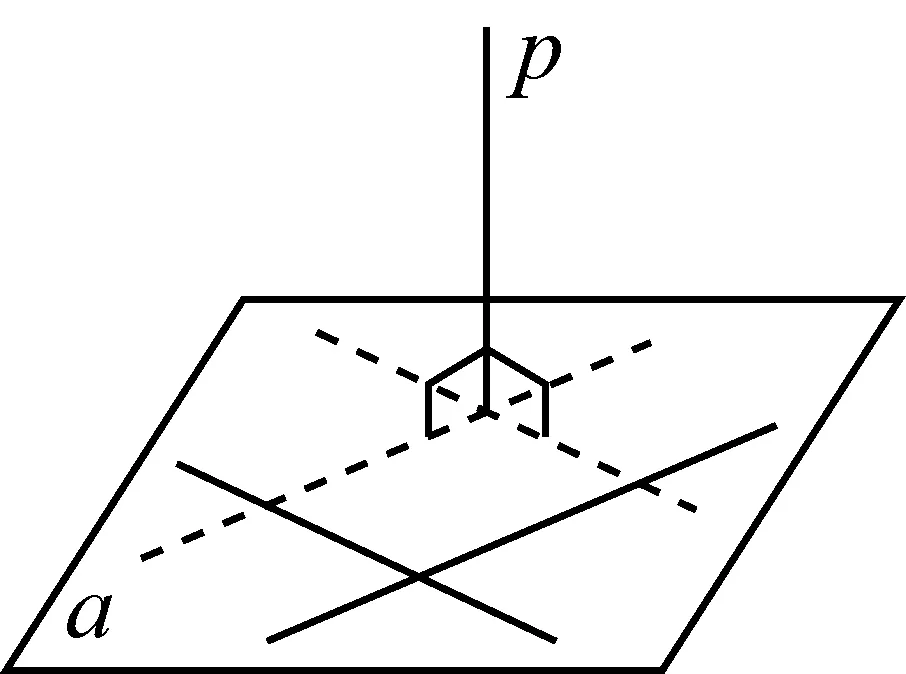
图10
总之,第一次“直线与平面垂直”的出现让学生们直观地了解直线与平面垂直,为以后的学习打下基础.第二、三次的编排很相似,均是在直线与平面的位置关系中进行讲解,之后也都进行深入,但第三次出现的高中定义限制了条件,即:①直线与平面相交;②直线垂直于过交点的两条直线.第三次与第四次的定义均出现在高中,值得关注的是,在这两次定义的叙述中都使用了“任意”这个数学中的学术语,相比于第二次出现的初中定义中使用的“所有”一词更具抽象性,从而印证了教科书的编写要适应学生认知发展的规律.同时,第四次的引入也为即将讲授的空间直角坐标系做准备,能够使学生更容易、清晰地理解空间直角坐标系中直线和平面、平面和平面的垂直关系.类似这样的内容设置在日本数学教科书中有很多,在此不赘述.
4 结语
教科书是学生学习知识、掌握技能、培养思维和形成人格的最基本的信息载体和工具,它的优劣对学校教育质量的提高是至关重要的.中小学数学教科书中相关知识的有效衔接是优秀教科书的标志之一.如果中小学教科书没有能够做到这一点,即使是对优秀的教师来说,在教学中衔接相关知识也是极为困难的.因此,小学数学教科书编写者应该熟知初高中数学内容,初中数学教科书编写者应该熟知小学和高中数学内容,高中数学教科书编写者也应该熟知小学和初中数学内容,这样才能保证小学、初中和高中数学教科书内容的有效衔接.从日本中小学数学教科书中立体几何内容的衔接看,既自然顺畅地逐次深入,又在潜移默化中降低了学生学习难度.通过对立体图形由表及里的认识,使学生对具体事物的认识层层递进,对具体事物的表征研究,探究其内在本质.这对培养学生的观察能力、动手操作能力和逻辑推理能力具有重要的促进作用.在初中《数学1》的“各种各样的立体”后有设置“正多面体”,在最后作为选修的“数学广场”部分又对“正多面体”进行讨论.在高中《数学A》中又系统讲解“正多面体”,并给出欧拉的多面体定理,即v-e+f=2,v为顶点数,e为边数,f为面数.在“卷末广场”的学习中也安排了正八面体的动手制作课题六项.通过这种编排,使学生对立体几何知识的掌握更具系统性和完整性,并注重学生的个体差异和个性发展.
中小学数学知识的有效衔接,是日本教科书的显著特色之一.另外,日本对教科书的编写过程稳中求进,十分缓慢,大约每十年进行一次改革,内容变化也不大.正如日本著名教育家佐藤学先生所说:“文化变革越是缓慢,才越能得到确实的成果.”*(日)佐藤学.静悄悄的革命[M].李季湄译.北京:教育科学出版社,2014:2.上述理念与做法对我国数学教育改革与数学教科书建设具有“他山之石,可以攻玉”之借鉴功效.
致谢:本文参考的日本现行教科书是由日本京都大学柳本哲教授和岐阜县教育委员会教育总务课下野宗纪先生提供,在此表示衷心的感谢.
