微言要义之抽样方法
2018-07-16徐章韬
张 灵 徐章韬
(华中师范大学数学与统计学学院 430079)
1 引言
数学家华罗庚指出“据我看来,要真正打好基础,有两个必经的过程,即‘由薄到厚’和‘由厚到薄’的过程,‘由薄到厚’是学习、接受的过程,‘由厚到薄’是消化、提炼的过程”.“把书读厚”是“把书读薄”的前提,在教学中,中学数学教师应在自身已经理解数学的基础上,引导学生通过理性思考深入挖掘数学知识本质、知识背后蕴含的思想以及知识之间的内在联系,把书读厚,而不能只停留在对知识的逻辑意义上的认可.教师的教学能力,首当其冲体现在对教学内容的把握上,若教师自身不具备“理解数学”的能力,教学过程必然表面化,无法对知识进行深入剖析、展开,那么数学家华罗庚提出的两个必经过程都不可能会发生.章建跃老师提出“理解数学是教好数学的前提”[1],指出了“理解数学”的重要性.
在中学所要教学的概率与统计中,“利用样本估计总体”是统计的核心思想,样本的代表性取决于所采取的抽样方法.中学阶段主要学习了三种抽样方法:简单随机抽样、系统抽样和分层抽样,本文是对这三种抽样方法的一个深入研究.
2 简单随机抽样
简单随机抽样方法是一种最容易理解的、最简单的抽样方法,没有复杂的抽样程序,当抽样框——抽样总体组成的集合确定的情况下,可直接抽取样本,如人们在日常生活中买水果时,想知道水果是否好吃,会选择从所有的水果中随机挑出一个,尝一尝来进行判断,这是一种非常自然的想法.简单随机抽样体现了“利用样本估计总体”最朴素的思想——样本来源于总体,若要获得所需样本,最简单的方法便是从总体中直接进行抽样.
当各个单元在总体中的地位相同时,各单元被抽到的机会相同是样本具有较好代表性的前提.简单随机抽样的定义为“一般地,设一个总体含有N个单元,从中逐个不放回地抽取n个单元作为样本,如果每次抽取时总体内的各个单元被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样”[2].在简单随机抽样中,可用条件概率的知识来解释每个单元被抽到的概率是相等的.
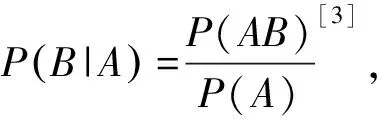
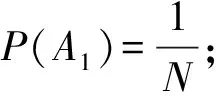
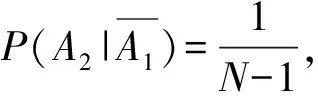
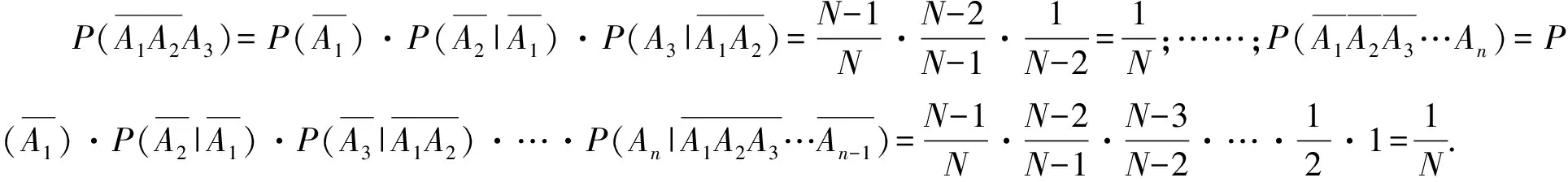
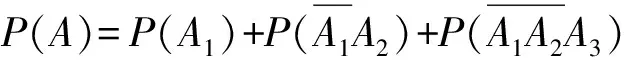
简单随机抽样的本质是一种随机现象,是系统抽样和分层抽样的基础.事实上,系统抽样和分层抽样都可看作是在进行简单随机抽样前多了一些不影响单元等概率性的前期处理工作:系统抽样是在进行简单随机抽样前,根据初始单元和抽样间距将总体分为了若干个地位相同的群;分层抽样是在进行简单随机抽样之前,按相关标志值将总体划分为了若干个层.简单随机抽样的随机性是系统抽样、分层抽样随机性的前提,它给人们提供了一个讨论概率抽样方法自然的出发点.
3 系统抽样
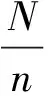
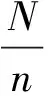
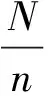
在词典里,“系统”指由若干相互联系、相互作用的要素所组成的、具有一定结构和功能的有机整体.在系统抽样中,起始单元确定了,再根据已经确定的抽样间距,便能得到其余的样本单元,整个样本也就确定了.这里的样本便可看作由起始单元和抽样间距确定的一个有机整体——“系统”,其结构表现为各单元在总体排列上的间距一定.这就像等差数列一样,首项(起点)定了,公差(间隔)定了,整个数列也就确定了.由于样本的结构一定,在系统抽样中,当总体单元排列顺序确定时,一些单元不可能同时出现在样本中,即排除了不符结构的样本组合.因此,与简单随机抽样相比,系统抽样抽取样本的方式虽然更加简便,且符合等概率性,但是其样本的多样性减弱了.另外,采用系统抽样方法从总体中抽取样本,系统抽样的精度(样本的多样性,代表总体的程度)与总体单元的排列顺序密切相关.
4 分层抽样
若总体是由差异比较大的几部分单元组成的,采用系统抽样或随机抽样都有可能产生分布不均的样本,这时,需要人为将总体分层,再按比例对每一层进行随机抽样,即采用分层抽样.中学数学介绍的是按比例分层抽样,其步骤为:①利用辅助信息,将总体N个单元分为“不重不漏的”m个层;②按照各层单元数占总体单元数的比例分配每一层的样本容量,样本总量为n;③采用简单随机抽样方法或系统抽样方法,从各层独立的抽取相应样本容量的单元;④将各层取出的单元合在一起作为样本[6].当各部分差异明显时,采用分层抽样方法能得到与总体结构相近的样本,其样本的代表性要高于简单随机抽样和系统抽样.
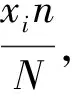
在分层抽样中,总体中差异明显的每一部分都会在样本中占有相应比例的单元数,保证了样本在总体中的分布是相对均匀的,层样本(各层所获的那部分样本)相对于所在层的代表性决定了最终样本的代表性.因此,就分层抽样而言,如何提高层样本的代表性是关键,这就要回归到简单随机抽样的特点.在简单随机抽样中,各单元之间的差异越小,即总体在标志值上的方差越小,各种可能的样本组合之间的差异也会小,随机抽取出的样本在估计值上相对于总体的偏差会越小,反之,总体在标志值上的方差越大,各种可能的样本组合之间的差异也会越大,随机抽出的样本代表性差的可能性越高.因此,在分层抽样中,为了提高层样本的代表性,应尽可能的利用辅助信息,扩大层间方差,从而降低层内方差,提高估计的精度.
5 教学建议
5.1 挖掘随机抽样的思想
合理的数学知识背后需要有思想的支撑,同样地,学生在学习数学知识时,也需要相应的数学思想作为支撑,站在思想的角度看待知识,认清知识“来自何方”.三种抽样方法都属于随机抽样,掌握随机抽样的思想,为学生深层次地理解知识奠定基础.
首先,抽样的目的是为了用样本估计总体,抽样方法往往只有“好与差之分”,而不是“对与错之分”,评价抽样方法的优劣应该以样本的代表性为标准;其次,样本的代表性,要从抽样规则来看,而不能以某一次的抽样结果是否与总体一致论,在随机抽样中,样本的产生是随机的,合理的抽样规则也可能产生歪曲的抽样结果,这里所提到的“样本的代表性”,是根据抽样规则进行理性分析后得出的理论结果;最后,为了使样本具有代表性,抽样规则应客观、公正,保证总体中每个单元被抽中的概率相等,不能人为的安排某些单元有更大的可能性被抽中,这样的抽样结果是不客观的.
5.2 把握知识的要点
在三种抽样方法中,何为“简单”、何为“系统”、何为“分层”,是需要把握的要点,要点往往是认识知识本质的关键所在.“简单”说明了简单随机抽样在三种抽样方法中的基础地位,“系统”指向系统抽样所得的样本是一个具有一定结构的有机整体,“分层”表明所得样本的结构与总体一致,在总体中的分布是相对均匀的.这些要点揭示了三种抽样方法的不同之处,以及各自的特点,认识了要点之后,还有助于对三种抽样方法的精度进行进一步的分析、比较,明确影响样本代表性的因素.
5.3 与概率知识相结合进行教学
统计与概率关系密切,对抽样方法的等概率性进行理性分析需要用到概率知识.严谨、理性是数学学科的特点,由于抽样方法与实际生活关系密切,看似简单、容易理解,教师教学时容易经验至上,忽视对这部分知识进行理性分析,这样的做法不利于培养学生的理性精神,这样的教学是不够深入的.借助概率知识,通过逻辑分析和运算过程,让三种抽样方法的“等概率性”变得有理有据,促进学生进一步体会抽样方法的科学、合理之处.
