基于Copula函数的新型综合干旱指数构建与应用

张　迎，黄生志，黄　强，李　沛，马　岚

（西安理工大学　西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048）

1　研究背景

干旱是制约人类社会发展的一大难题，干旱发生频率高，影响范围广，危害程度深，严重影响着人类的农业生产、经济发展及社会稳定。我国是一个自然灾害频发的国家。据统计，气象灾害造成的经济损失约占所有自然灾害的70%，其中干旱造成的损失又占了气象灾害的50%以上［1］。随着全球气候变暖，干旱发生的频率逐渐增高，影响逐渐增大，对干旱的深入研究刻不容缓［2-3］。为将干旱进一步量化，研究者们常采用影响干旱的气象、水文等要素建立不同的干旱指标，对干旱强度、持续时间、发生频率、影响危害等进行客观地时空比较，从而达到度量、对比和综合的研究目的［4-6］。可以说，干旱指数是干旱研究的基础。

针对不同类型的干旱（气象干旱、水文干旱、农业干旱和社会经济干旱等），研究者们构建了不同的干旱指数。包括用于描述农业干旱的作物水分指数CMI［7］、土壤水分亏缺指数SMDI（基于周尺度土壤水分）和蒸散亏缺指数ETDI（基于蒸散量）［8］，用来描述水文干旱的SWSI指数（基于积雪、水库蓄水、流量、降水和地表供水）［9］，以及用于描述气象干旱的基于标准化降水指数SPI［10］和PDSI指数（基于降水量、温度）［11］等。然而，干旱相关变量间存在一定差异性，使用单一指数无法综合描述气象、水文、农业、社会经济干旱的全部特征。因此，需要探索一种多变量的方法来解决这一问题［12］。近年来，为了创建一种融合多种干旱相关变量的综合干旱指数，国内研究者们付出了相当多的努力。任怡等采用熵权法赋权和模糊综合法将PDSI、SPI和SPEI这3种指数结合在一起，构建了一种模糊综合评价指数DI［13］；常文娟等基于主成分分析法构建了融合降雨、径流及土壤含水量等水文气象要的综合干旱指数PRSM［14］。然而，基于赋权法、模糊综合法的综合干旱指数在赋权时存在一定主观性，极易造成误差。基于主成分分析法的综合干旱指数则是将相关变量线性组合在一起，无法反映它们的非线性影响特征。Copula函数是一种能够将不同边缘分布的相关变量结合在一起的连接工具，能巧妙的避免上述问题，且在水文水资源领域中已有较广泛应用［15-17］。基于此，本文拟构建一种基于Copula函数的综合干旱指数MSDIp（Multivariate Standardized Drought Index，parametrically），通过构建以降雨和径流作为边缘分布的联合分布函数，以求克服基于赋权法的综合干旱指数的主观性问题和主成分分析法针对非线性相关变量失真的问题。该指数能综合表征气象干旱和水文干旱的联合特征，提高综合干旱指数的准确性和适用性，以期为决策者监测、预防干旱提供有力支持。

2　研究内容与方法

2.1研究区概况及数据资料渭河是黄河的第一大支流，发源于甘肃鸟鼠山，流经甘肃、宁夏、陕西三省，在陕西省潼关县汇入黄河，全长818 km（图1）。渭河流域位于东经103.5°～110.5°，北纬33.5°～37.5°之间，流域面积13.5万km2。整个流域地势西高东低，北部为黄土高原，南部为秦岭山脉。渭河流域属大陆性气候，冬季寒冷少雨，夏季炎热多雨，年平均气温为7.8～13.5°C，年降水量为500～800 mm，主要集中在6—10月，蒸发较为强烈，陆面蒸发量为500 mm，水面蒸发量为660～1600 mm，区域年平均降水量约为559 mm，近几十年来有下降的趋势，渭河多年平均径流量75.7亿m3，陕西境内为53.8亿m3［18-20］。

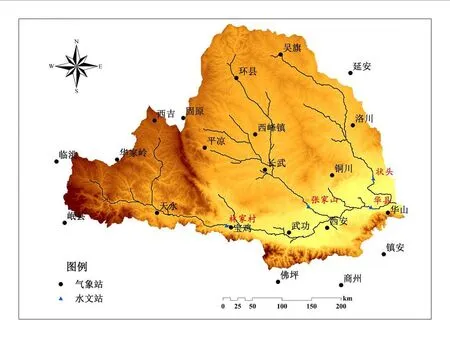
图1　渭河流域水文、气象站点分布图

本文选取由中国气象局国家气候中心获得的渭河流域21个气象站观测降水记录，记录以日为时间步长，覆盖从1960年到2010年。渭河流域径流资料来源于黄河水利委员会，包括主要干流和支流上的林家村、张家山、华县和状头等多个水文站的日径流序列。如图1，本文将渭河流域划分为3个区域进行研究，分别为张家山以上流域（泾河流域）、林家村以上渭河流域和全流域。

2.2研究方法本文选取降雨（气象要素）、径流（水文要素）两种变量，利用Gringorten（1963）经验频率公式分别计算二者的边缘分布［21］，采用Frank Copula函数计算其联合概率分布，从而构建出既能表征气象干旱，又能表征水文干旱的综合干旱指数（MSDIp）。在此基础上，结合北极涛动、Nino3.4区海温等大气环流异常因子和太阳黑子活动，探究了干旱演变的可能驱动力。

2.2.1二维Copula函数理论Copula函数能够构造不同边缘分布的多个变量的联合分布函数。在众多Copula家族中，阿基米德Copula应用范围最为广泛［22］。而阿基米德Copula函数当中，以Clayton Copula、Gumbel Copula和Frank Copula应用最广。其中，Frank Copula结构较为简单，可以用来描述对称相关结构，对于正负相关性均可适用且对相关性的程度没有限制，上下尾相关性变化均不明显［23］，而其他两种Copula函数只适用于正相关的水文序列，且都着重反映上、下尾中某一尾的尾部相关性［23］。然而，受冰雪融水、流域调蓄等作用，降雨、径流序列关系并不一定为正相关。同时，Frank Copula函数在干旱研究中已有较多应用［12，24-28］。因此，本文选择Frank Copula函数作为连接函数，构建降雨、径流的联合分布。

根据Sklar定理，令F、G分别为随机变量x，y的边缘分布函数，H为联合分布函数，则对∀x,y∈ Rˉ，有Copula函数C使得：

若F、G连续，则C是唯一的。

函数最早由Frank于1979年提出，其表达式为：）

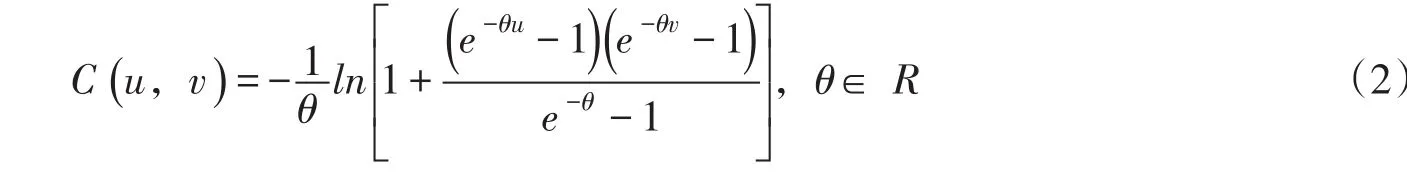
生成元为：

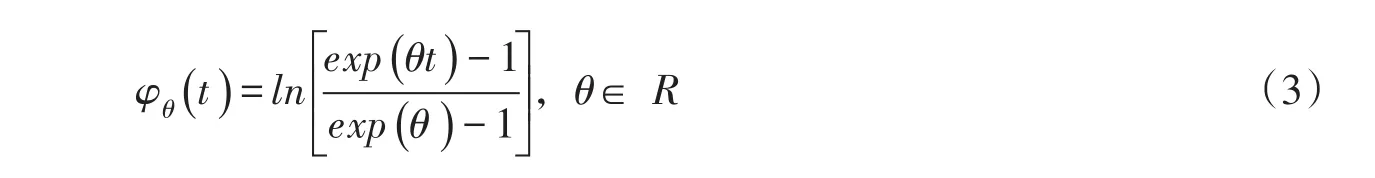
式中：u和v分别为两个变量的边缘累积概率，θ为参数。θ可以由Kendall秩相关系数τ求得：

一阶德拜函数D1(θ)表达式为［29］：

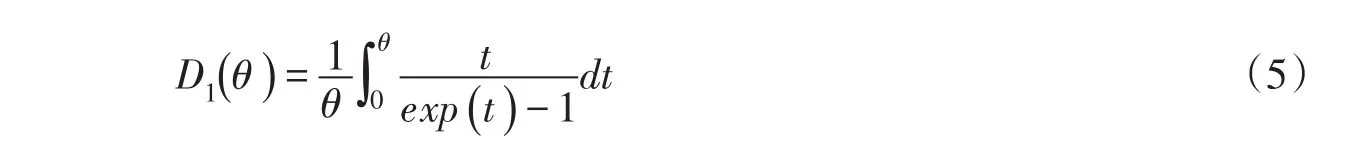
2.2.2综合干旱指数（MSDIp）的建立分别以渭河流域各区域降雨、径流序列为随机变量x和y，通过皮尔逊相关系数法算得各区域降雨、径流的相关系数在0.63左右，具有较强的相关性，可以进行联合分布函数的构建。X和Y为降雨、径流的某一数值，假设两随机变量相应的边缘分布分别为F（x）和G（y），则它们的联合分布P可以用累积联合概率p和Copula函数C表示为：

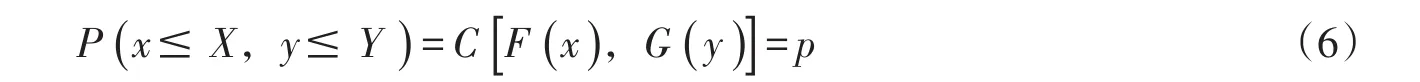
于是，由联合分布函数得到综合干旱指数（MSDIp）：

式中φ为标准正态分布。

由于气象干旱的（缺乏降水）发生和结束都很迅速，而水文干旱（径流不足）的开始与结束对气象干旱的响应存在一定的延迟［8］，往往气象干旱已经结束了，水文干旱才刚刚开始。这使得决策者难以兼顾多种类型干旱的情况，做出及时、合理、有效的应对决策。MSDIp既包含降雨信息，又包含径流信息，可以同时表征气象干旱和水文干旱，综合了SPI指数善于捕捉干旱开始的优点和SRI指数善于捕捉干旱结束的优点。按照严重程度，可以将干旱划分为湿润、无旱、中旱、重旱、特旱等不同等级。本文参照SPI指数等级划分方法，将MSDIp指数的干旱等级划分如表1。考虑到干旱达到一定程度才会产生较大影响，根据历史干旱发生频次与MSDIp指数的经验频率，以MSDIp=-1作为判定干旱是否发生的阈值，即当MSDIp指数持续小于-1时，则认为发生了干旱。

表1　MSDIp干旱等级划分

2.2.3时空演变特征分析本文基于构建的1960—2010年年尺度MSDIp指数序列，分析了渭河流域3个区域综合干旱的时空演变特征。采用了Man-Kendall法与极差重标法（R/S）结合的综合趋势分析法［30］分析了综合干旱指数的趋势与持续性；采用启发式分割法［31-32］计算了1960—2010年序列的变异发生点。

将前文所得月尺度的MSDIp指数转化为年尺度MSDIp指数，得到新的时间序列。

用Mann-Kendall法分析时间序列的趋势，计算出统计特征值U，从而判断序列的趋势特征：特征值U＞0时，表明有上升的趋势；U＜0时，表明有下降的趋势；并且，当|U|＞U0.05/2=1.96时，表示序列趋势变化显著。

用R/S法求出赫斯特指数H，以此指出序列的持续性或反持续性特征，即可得到序列可能的未来变化趋势。如果H＞0.5时，即具有持续性，未来变化趋势与该序列过去趋势相同；如果H＜0.5时，即具有反持续性，未来的变化趋势与该序列过去趋势相反。综合两个统计量（如表2），就可以得出干旱序列未来的趋势特征［30］。

2.2.4基于交叉小波的驱动力分析利用交叉小波功率谱（XWT）［33-35］，采用Morlet小波进行计算，分别对Nino3.4区海温（ENSO）、北极涛动（AO）等大气环流异常因子和太阳黑子活动，即m（t）与MSDIp指数n（t）进行分析研究。根据交叉小波功率谱定义，有：

表2　综合法未来趋势特征

式中：a为尺度伸缩参数；τ为时间平移参数；CM(a，τ)是序列m（t）的小波变换系数；CN(a，τ)是序列n（t）的小波变换系数的共轭复数。

交叉小波功率谱能够反映两个序列经过小波变换后具有相同能量谱区域，从而揭示两序列在不同时频域上相互作用的显著性。

3　结果及其分析

本文计算了月尺度下的SPI（标准化降水指数）、SRI（标准化径流指数）和MSDIp指数，通过对比验证了MSDIp指数表征干旱的优越性，进一步采用MSDIp指数的年均值分析了渭河流域干旱时空演变特征，并分析了干旱演变的驱动力。

3.1MSDIp指数的应用效果分析各区域Frank Copula参数θ取值计算结果如表3。

表3　各区域参数θ计算结果

图2（a）展示了月尺度下的渭河流域全流域1960—2010年的SPI指数、SRI指数和MSDIp指数。从图2（a）可知，月尺度下MSDIp指数的走势、变化规律与SPI指数和SRI指数有较好的一致性。MSDIp指数与SPI指数、SRI指数的Pearson相关系数均在0.8以上，呈极强相关，且通过了95%的置信度检验。这说明新构造的MSDIp指数具有一定的可靠性。

为进一步作更直观的比较，截取1972至1982年月尺度下的SPI指数、SRI指数和MSDIp指数变化情况如图2（b）所示。将横坐标放大，可以看出3种指数的一些差异。一般认为，干旱的开始通常是由于降雨的持续缺乏，因此SPI指数对于捕捉干旱的开始非常灵敏；而由于复杂的产汇流过程，水文干旱对气象干旱的响应存在一定的延迟，因此SRI指数能有效识别干旱的持续时间和结束。如图2（b）中黑色矩形框所示，MSDIp和SPI指数小于-1的时刻（认为是干旱发生的开始）相对SRI指数来说要早，这表明MSDIp指数捕捉干旱开始的能力与SPI指数相当。同时，MSDIp和SRI指数大于-1的时刻（认为是干旱发生的结束）相对SPI指数来说要迟，这表明MSDIp指数捕捉干旱结束的能力与SRI指数相当。这是因为，SPI指数以气象干旱特征为主要参考，而气象干旱发展突然、迅速；SRI指数以水文干旱特征为基准，而水文干旱存在相当的延迟且持续时间较长。图中黑色矩形框内显示，MSDIp指数能够将SPI指数和SRI指数所捕捉的干旱开始与结束都含括在内。也就是说，MSDIp指数能够如SPI指数一样很好的捕捉到干旱的开始，也能如SRI指数一样很好的捕捉到干旱的持续时间和结束，同时具有二者的优点。此外，由图中第二个矩形框内3种指数变化情况可以看出，只发生了水文干旱而气象干旱未发生的情况下，MSDIp指数同样捕捉到了干旱的发生。这些结果有力地证明了MSDIp指数综合了降雨径流两种信息，能够灵敏、有效地捕捉干旱发生的开始、持续时间、结束。

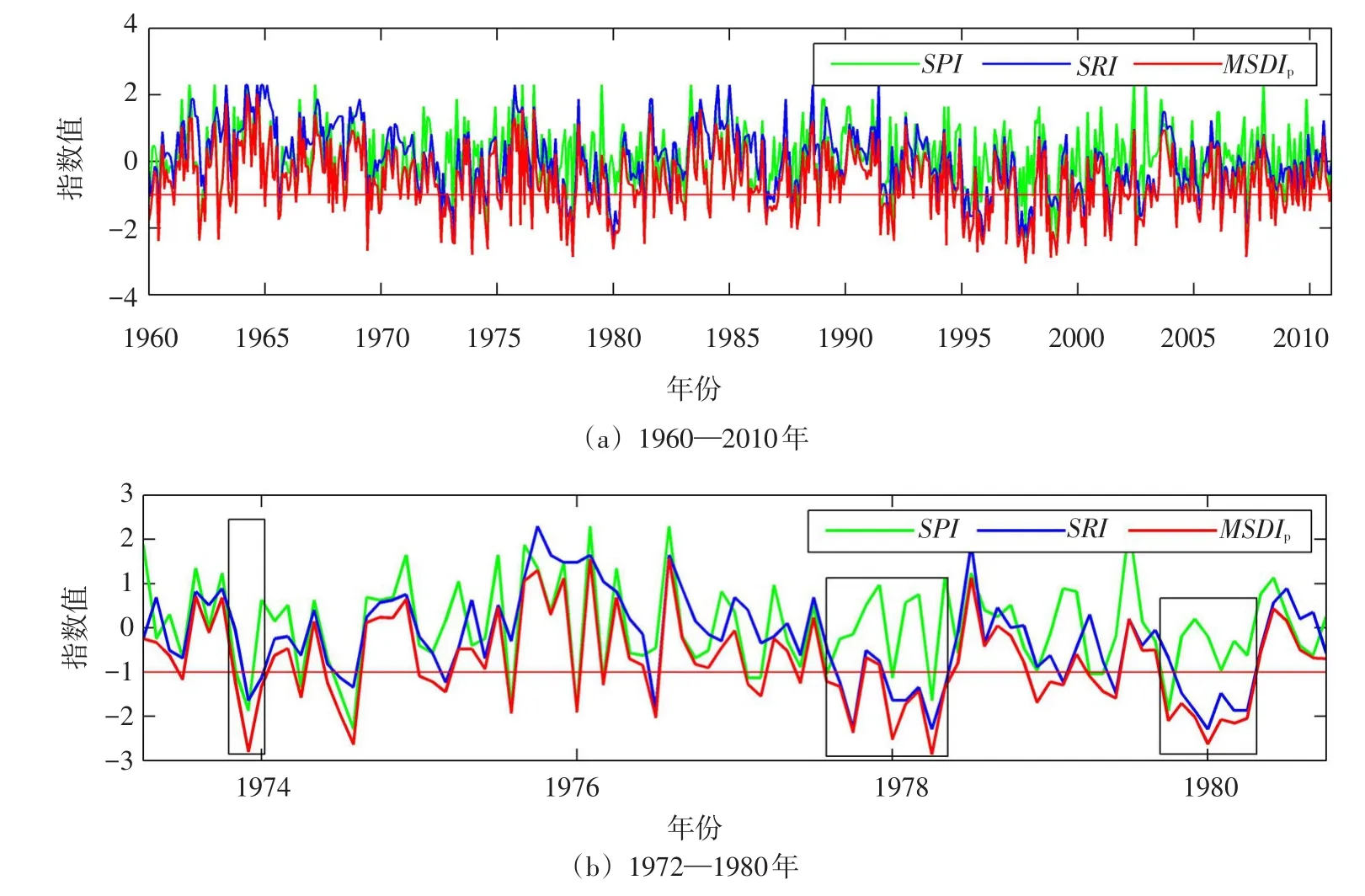
图2　渭河流域全流域月尺度下不同时段SPI指数、SRI指数、MSDIp指数对比

由图2（a）中MSDIp指数年际变化可知，1972年至1982年左右，干旱发生较为频繁，且干旱等级较高，同样的还有1995年至2007年左右。查阅渭河流域干旱相关文献资料，发现本文所研究MSDIp指数捕捉到的干旱与有历史记载、文献支持的干旱事件能够相吻合［36-37］，这说明新构造的MSDIp指数具有一定的准确性。

同时，观察图2发现，表示MSDIp的红色折线总体上位于表示SPI的绿色折线和表示SRI的蓝色折线的下方，这体现出MSDIp在数值上对干旱的一种“严重化”。分别对样本总数为612（51年×12月）的MSDIp指数序列、SPI指数序列和SRI指数序列进行数值、干旱场次相关统计（如表4），发现：

（1）MSDIp至少与SPI、SRI中的一种同时小于-1的有164次，“报准率”达75.2%，说明MSDIp指数具有一定的可靠性。

（2）MSDIp＜-1，而SPI、SRI均≥-1的有54次。这54次“误报”大体上可以分为三种情况：SPI＞0，SRI接近-1；SRI＞0，SPI接近-1；SPI、SRI均小于0，但均大于-1。在这三种情况下，SPI与SRI虽均未达到阈值，但从综合干旱的角度考虑（由于干旱是包括降雨、径流等多种因子在内的水分亏缺，仅考虑气象干旱或水文干旱，难以反映流域真实干旱情况［5］），无法得出此种情况较SPI或SRI一方小于-1而另一方大于0的情况更为乐观的结论。进一步对这54次“MSDIp显示为干旱而SPI、SRI显示为非干旱”的情况进行分析，发现在其前后一个月内发生气象/水文干旱的有26次。这说明，MSDIp指数在干旱预警方面具有较好的表现。

表4　MSDIp、SPI、SRI干旱场次统计结果

总的来说，本文构建的基于Frank Copula函数的综合干旱指数MSDIp具有一定的可靠性、灵敏性和综合性等优越性，兼具SPI指数和SRI指数两种指数对于捕捉干旱开始、结束的优点，能够更加综合、全面的识别干旱，提前发出预警，为干旱的检测与防治提供有力的支持。Hao等［38］也通过将不同时间尺度的美国加利福尼亚州和北卡莱罗纳州的综合干旱指数与SPI指数和SSI指数进行对比分析，比较了它们捕捉的干旱发生时间和持续时间，从而验证了综合干旱指数的可靠性，且具备有效的干旱预警能力。另外两个区域（林家村以上流域与张家山以上流域）所得结果与全流域大致相同，此处不再一一赘述。

3.2渭河流域综合干旱时空演变特征分析本文基于构建的1960—2010年年尺度MSDIp指数序列，分析了渭河流域3个区域综合干旱的时空演变特征。

3.2.1综合干旱过去趋势分析分别对林家村以上流域、张家山以上流域、全流域3个研究区域MS⁃DIp指数进行分析，得到结果如表5。

表5　研究区域综合干旱过去趋势及未来趋势结果

由表5可知，在1960—2010这51年中，林家村以上流域、张家山以上流域和全流域的干旱指数均存在显著下降趋势（U＜-1.96）。这说明从1960年到2010年，渭河流域干旱逐步加剧，造成的影响也愈加严重。进一步采用Mann-Kendall法对各区域降雨、径流序列进行趋势分析，发现降雨序列的特征值U降雨=-1.6，说明降雨序列存在不显著下降趋势；径流序列的特征值U径流=-3.7，说明径流序列存在显著下降趋势。可见，过去50余年渭河流域的降雨和径流均有不同程度的减少，其中，径流的减少是造成渭河流域综合干旱加剧的主要原因。而降雨和径流的变化受到气候变暖与人类活动的双重影响。

上述干旱变化情况，与以往关于渭河流域干旱演变特征的研究能够互相印证，如：黄生志等［31］采用SPI指数研究了渭河流域干旱特征演变，发现整个渭河流域干旱趋势明显，流域的中部和东部地区的干旱严重程度有上升趋势；任立良等［18］采用SRI指数基于VIC模型研究了渭河流域水文干旱演变特征，发现渭河流域年降水量呈下降趋势，年径流量均呈显著减小趋势，且1970年代和1990年代流域总体呈现干旱频发的特征；赵安周等［20］利用PDSI指数基于SWAT模型研究了渭河流域干旱时空分布，发现渭河流域、渭河干流和泾河流域均表现为变干的趋势。因此，变化环境下流域综合干旱的演变研究尤为重要。

3.2.2综合干旱的变异诊断采用启发式分割法对林家村以上区域、张家山以上区域、全流域1960—2010年年尺度MSDIp指数进行变异诊断，取P0=0.95，ℓ0（序列分割长度）为25，均存在变异点，P（Tmax）=1＞P0，且变异点都发生在1994年；对全流域进行第二次分割，有P（Tmax）=0.959＞P0，得到第二变异点发生在1971年。根据已有研究［31］可知，渭河流域MSDIp指数变异点与径流序列变异点基本一致。因此，渭河流域综合干旱的变异可能是由径流序列的变异导致的。各区域变异点情况如图3所示。

3.2.3综合干旱的未来趋势分析结合前文所述1960—2010年渭河流域综合干旱过去趋势分析结果，进一步分析渭河流域综合干旱的未来趋势。由前文中表5可见，林家村和全流域Hurst指数H均大于0.5，下降趋势有持续性，未来依然为下降趋势；与之相对的，张家山以上流域Hurst指数小于0.5但接近0.5，存在较弱的反持续性，也即未来反而存在上升趋势。而MSDIp指数越小，说明越偏向干旱。也就是说，渭河流域除张家山以上流域综合干旱情况可能会有所减缓外，其他区域均存在加重的趋势，林家村以上流域最为严重。值得庆幸的是，3个区域Hurst系数均接近0.5，说明按照这种变化趋势发展的可能性并不大。但这种趋势仍然需要引起重视，一旦这种趋势成为现实，将给当地农业、经济、社会等的可持续发展带来极大的挑战，因此需要政府部门提前采取相应的措施以减缓、应对综合干旱可能加重的情况。

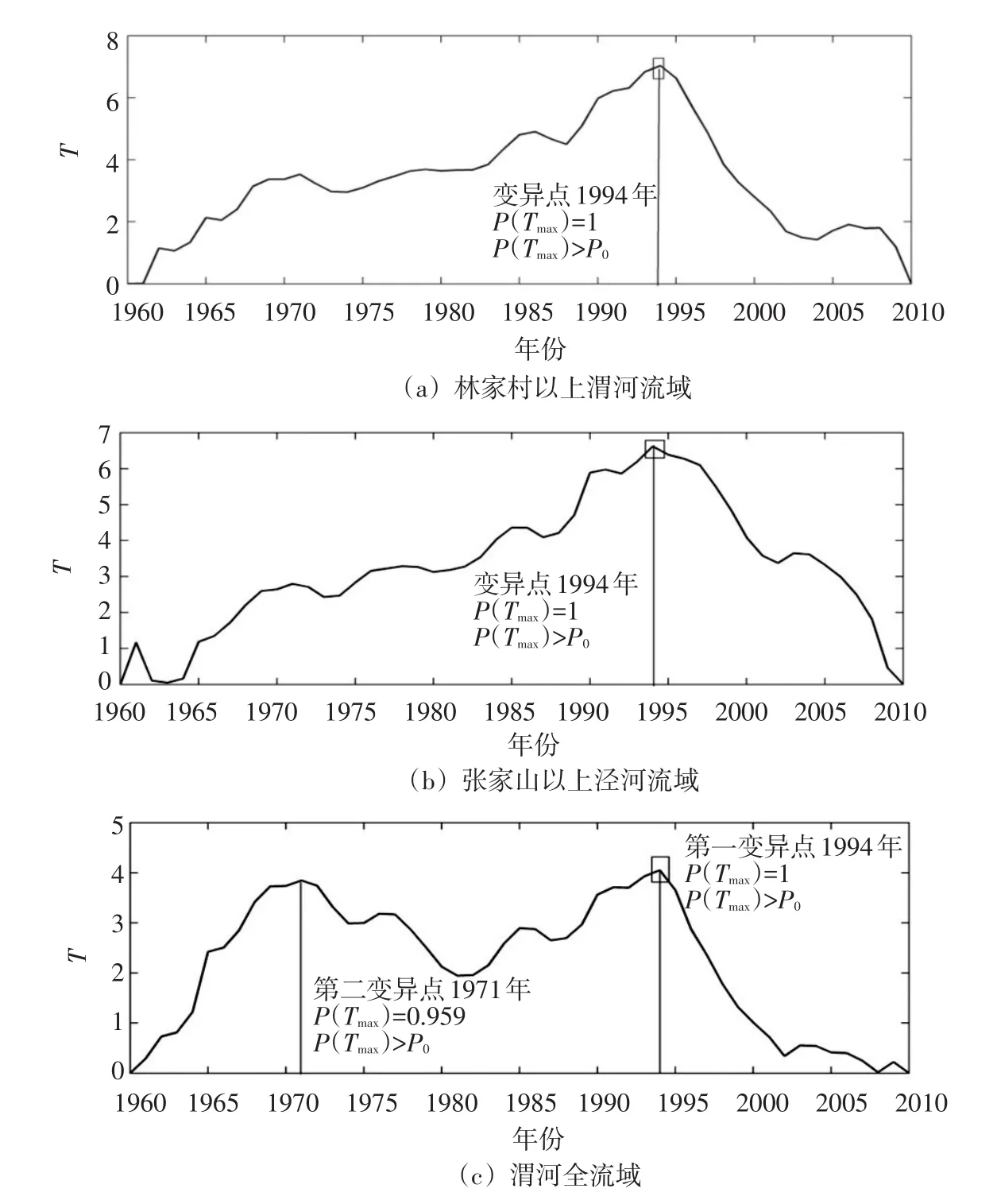
图3　流域年径流启发式分割检验

3.3综合干旱演变的驱动力分析由前文知，渭河流域综合干旱存在变异，且干旱情势未来有着加剧的趋势。为探究造成此影响的原因，本文采用交叉小波法对干旱演变的驱动力进行了分析，并对驱动因子间的相互关系进行了研究。本文选取北极涛动（AO）、Nino3.4区海温（ENSO）和太阳黑子3种对降雨、径流影响较大的气象因子［39-41］，分别分析了它们对干旱指数的影响。

图4—6为大气环流异常因子及太阳黑子对全流域MSDIp指数的小波图谱。图中细黑线为小波影响锥线的边界，为有效谱值区；区内粗黑线为显著性水平95%的置信区间；箭头表示相位差，箭头向右表示两时间序列变化相位一致，箭头向左表示两时间序列变化相位相反，箭头向上（90°）表示气象因子变化超前干旱指数变化3个月，箭头向下（90°）表示气象因子变化落后干旱指数变化3个月。小波变换系数越大代表相关性越高，即颜色越红意味着相关性越高。

3.3.1北极涛动（AO）对综合干旱指数的影响AO是北半球热带外大气低率变化的主要模态，我国北方的气候异常与AO有着密切联系［40］。由图4可知，北极涛动（AO）与全流域MSDIp指数在1960—1970年有周期为1到4年的正相关关系，在1982—1988年有周期为6到8年的正相关关系，在1992—1994年有周期为4年的正相关关系，在1996—1998年有周期为1到2年的负相关关系。总的来说，AO对全流域MSDIp指数影响较为强烈，呈显著正相关关系。

3.3.2Nino3.4区海温对综合干旱指数的影响ENSO是低纬度地区热带海气耦合系统中最强的年际变化信号，海温的异常变化对大气环流和我国天气气候变异起着重要作用［42］。Nino3.4区海温是EN⁃SO的特征指数。如图5所示，Nino3.4区海温与全流域MSDIp指数在1962—1974年有周期为1到4年的正相关关系，在1984—1993年有周期为4到6年的正相关关系，在1994—1996年有周期为2到4年的正相关关系，在1996—1997年有周期为1到2年的负相关关系。Nino3.4区海温的影响则略弱于北极涛动。3.3.3太阳黑子对综合干旱指数的影响太阳变化是通过调节宇宙射线通量的变化，影响地球上空云量的变化，最终影响气候变化的［43］。如图6，太阳黑子与全流域MSDIp指数在1970—1985年有周期为7到11年的负相关关系，在1985—2005年有周期为7到12年的正相关关系。由图中置信区域色相变化可以看出，太阳黑子对全流域MSDIp指数影响最为强烈。

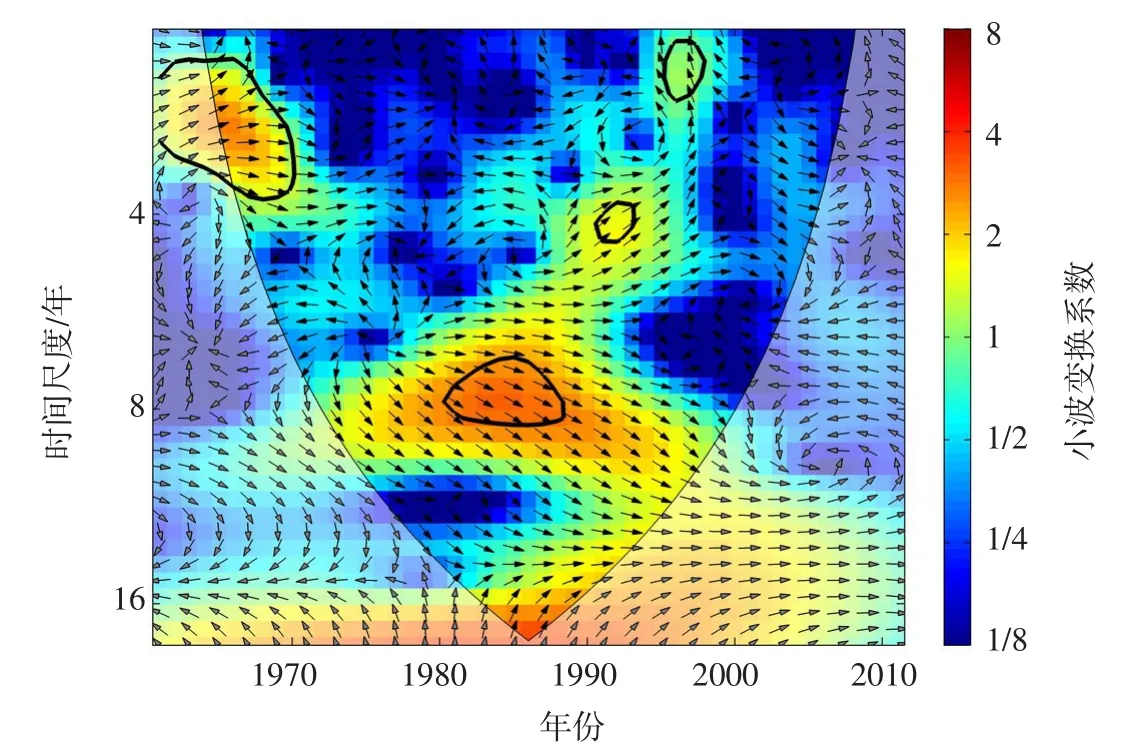
图4　AO与全流域MSDIp指数交叉小波关系图谱

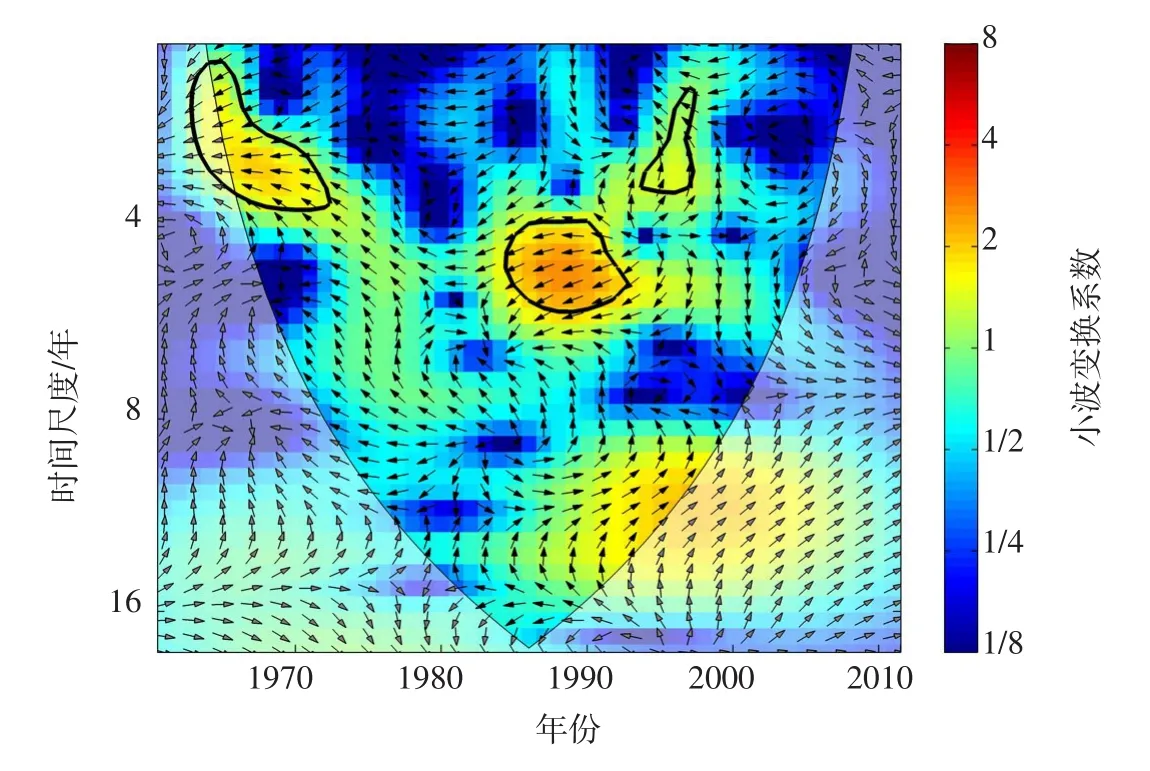
图5　Nino3.4区海温与全流域MSDIp指数交叉小波关系图谱

此外，进一步分析太阳黑子与AO、Nino3.4的关系（如图7、图8），可以发现，太阳黑子对二者的影响也极为强烈。太阳黑子与AO在1970—1980年有周期为7到11年的负相关关系，在1981—2006年有周期为7到14年的正相关关系。太阳黑子与Nino3.4在1970—1994年有周期为10到14年的正相关关系，在1990—2004年有周期为8到10年的负相关关系。林家村以上流域与张家山以上流域情况与之大体相同。

通过对比发现，对综合干旱的影响程度：太阳黑子活动＞Nino3.4区海温＞AO。现有研究表明，太阳黑子活动对降水、径流均存在影响［40，44］，故而对基于降水、径流序列构建的MSDIp指数，也就是对综合干旱，存在直接影响。同时，太阳黑子活动也通过影响大气环流异常因子，对MSDIp指数造成间接影响。由此可见，太阳黑子活动是影响渭河流域综合干旱演变的主要驱动力。

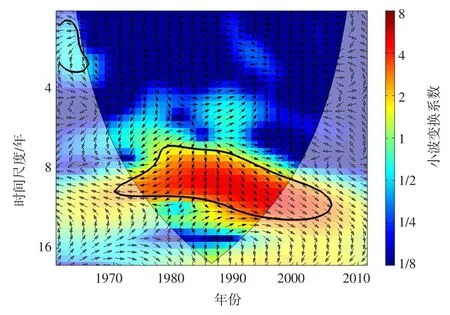
图6　太阳黑子与全流域MSDIp指数交叉小波关系图

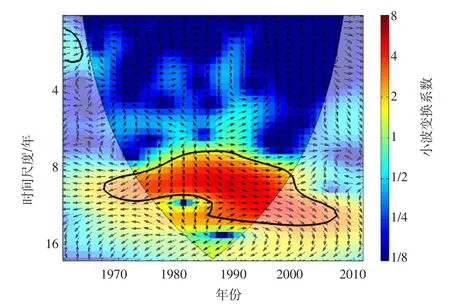
图7　太阳黑子与AO交叉小波关系图谱

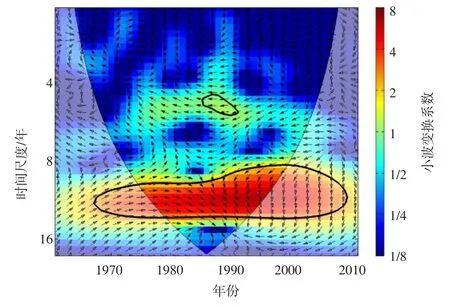
图8　太阳黑子与Nino3.4区海温交叉小波关系图谱

4　结论与讨论

本文根据渭河流域1960—2010年降雨、径流资料，构建了一种基于参数Copula函数的新型综合干旱指数，这种新型干旱指数避免了构建多变量联合分布函数时各边缘分布不同的问题、赋权法产生的主观性误差和主成分分析法对非线性关系失真等多种弊端，能够较好地综合表征气象与水文干旱，具有以往干旱指数所没有的优越性。通过MSDIp指数在渭河流域的应用，可以得出以下结论：

（1）通过与SPI指数和SRI指数结果进行对比，MSDIp指数能够如SPI指数一样很好的捕捉到干旱的开始，也能如SRI指数一样很好的捕捉到干旱的持续时间和结束，同时具有二者的优点。这意味着，MSDIp指数能够综合的表征气象、水文两种干旱，为干旱的监测、防治乃至预报提供可靠、有力的支持。

（2）1960—2010年间，渭河流域各区域综合干旱均存在显著加剧趋势，造成这种趋势的可能原因是渭河径流的显著减少。

（3）渭河流域综合干旱存在变异，主要变异点发生在1994年。且流域综合干旱未来情势不容乐观，整体上有加剧的趋势，应及时考虑采取有效措施应对这种可能发生的变化。

（4）渭河流域综合干旱的演变受大气环流异常因子和太阳黑子活动的共同影响。其中，太阳黑子活动是主要驱动力。太阳黑子活动既能直接影响渭河流域综合干旱的发生，同时也能够通过影响大气环流异常因子进一步产生间接影响。

本文提出MSDIp指数，旨在对传统的干旱指数进行补充，为决策者提供一种更加便利的、具有综合性的干旱指数。此外，本文尚存在一些不足。本文仅考虑了气象干旱与水文干旱两种干旱，而未能将农业干旱与社会经济干旱也综合进来。同时，本文仅能验证所使用的Frank Copula函数在渭河流域的适用性，而未能建立一种广泛通用的方法来构建综合干旱指数。

干旱已成为当下热门研究内容，而综合干旱指数方面尚需更多科学、有效的研究，以求为有关部门提供更加准确、可靠的决策依据，达到防治干旱的目的，甚至化灾为利，促进社会的可持续发展。