如何做实证:路径分析
2018-07-14喻平
喻 平
(南京师范大学课程与教学研究所 210097)
在回归模型中,可以包括多个自变量,但只能包括一个因变量.而许多因果效应问题,因变量往往不止一个.回归分析还有一个局限就是只能分析直接效应,不能分析间接效应.事实上,许多变量之间可能有直接关系,也可能受到中介变量的影响而产生间接效应.路径分析就是解决这类问题的方法.
路径分析的主要目的是检验一个假想的因果模型的准确和可靠程度,测量变量间因果关系的强弱,回答下述问题:①模型中两变量X与Y间是否存在相关关系;②若存在相关关系,则进一步研究两者间是否有因果关系;③若X影响Y,那么X是直接影响Y,还是通过中介变量W间接影响,或者既有直接影响也有间接影响;④直接影响与间接影响两者大小如何.
1 路径分析的基本概念
(1)路径图
用矩形框表示可观测的变量(图1),直线箭头表示假定变量之间有因果关系,箭头由自变量(原因变量)指向因变量(结果变量).双向箭头表示两个变量之间的相关关系,不是因果关系.如果变量之间没有连线,表示假定变量之间没有直接关系.
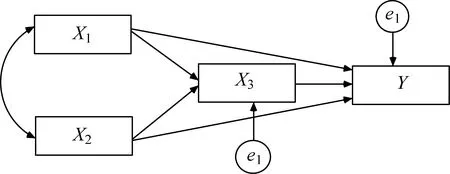
图1 四个变量的路径图
(2)外生变量
只能是原因的变量,有箭头指向別的变量但沒有箭头指向它.图1中X1,X2是两个外生变量.两个外生变量间可能有相关,以双向箭头表示,如X1与X2.两个外生变量间也可能独立无关,此时没有箭头表示.
(3)内生变量
为结果的变量,有箭头指向它.图1中的X3,Y都是结果变量.内生变量包括:中介变量:既是果又为因(X3);因变量:只为果的变量(Y).
(4)残差变量
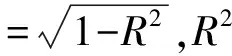
(5)路径系数
路径系数是指某一自变量对其因变量的直接效果,亦即标准回归系数.回归系数标于各路径上.由Xj到Xi的路径系数,它表示Xj与Xi间因果关系的强弱,即当其他变量均保持不变时,变量Xj对变量Xi的直接作用力的大小.
2 路径分析的设计
路径分析是多元回归分析的延伸,与后者不同的是:①路径分析中的因果关系是多层次的,因果变量之间加入了中介变量,使路径分析模型较一般回归模型对于现实因果关系的描述更丰富有力.②路径分析不是运用一个而是一组回归方程,在分析时更应注意保证各方程式所含意义的一致性.
路径分析要以下列假定为前提:①变量间的因果关系是单向的,不具有反馈性,又称递归模型;②变量间具有线性可加关系;③变量具有等距以上测量尺度;④所有误差均为随机的,外生变量无测量误差;⑤所有内生变量的误差变量间及与内生变量有因果关系的所有自变量间无相关.当某些假定,如递归性或变量的测量尺度不满足时,要做适当的处理才能应用路径分析.
2.1 适合路径分析的课题
讨论多于两个变量之间的关系,可以进一步思考它们之间是否有因果关系,此时可以考虑研究它们之间的回归分析和路径分析.例如,有三个变量X1,X2,X3,发现它们之间有比较高的相关,于是进一步思考它们之间的因果关系,可能会出现图2的一些情形:
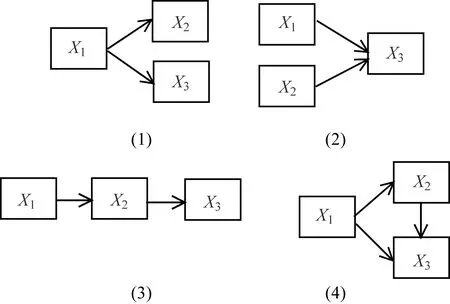
图2 三个变量之间可能的关系
图2(1)中,X1是因,X2,X3是果;图2(2)中,X1和X2是因,X3是果;图2(3)中,X1是X2的因,X2是X1的果,同时X2是X3的因,X3是X2的果,此时,X2成为X1到X3的中介变量;图2(4)中,X1是X2和X3的因,同时X2是中介变量.
例如,要研究三种数学核心素养:数学建模、逻辑推理、数学运算之间的关系,作相关研究方法发现它们之间有显著的相关关系,于是可以考虑以逻辑推理和数学运算为因,数学建模为果建立一个路径分析模型.这种考虑主要是因为相对于数学建模来说,逻辑推理和数学运算是更为基本的数学能力,因而它们可能会对数学建模产生影响.即数学建模能力会受到个体逻辑推理能力和数学运算能力的影响.
一般说来,要研究三个或三个以上变量之间关系的问题,在发现它们之间存在相关关系的基础上,都可以考虑用路径分析方法对其研究.例如,数学学习的各种心理因素:知识表征、认知结构、模式识别、自我监控、学习焦虑、成就动机、学习归因、学习兴趣、意志品格、自我效能、自我概念等等;数学学习的各种行为:学习的主动性、学习策略、学习习惯、学习风格、学习倦怠等等.这些因素之间可能就有相关关系,于是可以设计路径分析作进一步研究.
要确定采用路径分析方法研究的课题,首先,要确定研究这些变量的可能性和必要性,不能把任意几个变量组合起来作为研究对象,要思考它们之间是否可能相关,它们中谁可能是原因,谁可能是结果,谁可能是中介变量.这个分析过程或者依据某种理论,或者在别人已有的研究工作基础之上的拓展与推广,或者源于教学实践的经验.第二,对于决定要研究的变量,还要考虑是否有测量这些变量的公认比较好的量表.如果没有现成的量表,那么你是否能够编制所需量表,工具是关键.
2.2 路径分析步骤
(1)提出初始理论模型
研究者根据相关理论、文献数据或个人经验建构一个可以检测的初始模型,并绘制一个没有路径系数的路径图.这一步是整个研究的起点,要求建构的模型有一定理论依据,并根据经验分析外生变量的确可能会对内生变量产生作用.
(2)编制量表进行测验
在构建的模型中,涉及几个变量,就要编制几个量表.例如,图1中涉及的变量有X1,X2,X3,Y,于是要编制测量这四个变量的量表,然后选择一组被试进行测试,将数据收集整理.
(3)计算路径系数
路径系数是自变量(外生变量)对因变量(内生变量)的回归系数,直接作用关系是一元线性回归,间接关系是多元线性回归.因此,计算路径系数就是求回归方程的过程.路径系数的计算:第一步,将路径模式分解为数个回归方程式;第二步,求各回归方程式中各个预测变量的β值,各预测变量的β值即为所对应之路径系数.
(4)理论评估与修正
评估理论模型时可以删除不显著的路径系数,然后重新计算新模型的路径系数.在删除部分影响的路径后,会成为一种限制模型,由于预测变量数的改变,路径系数也会发生变化,因而要重新作回归分析.
案例1学生亲社会和反社会课堂行为对他们学业成绩的影响.[1]
研究者温兹尔提出研究问题:当考虑到学业行为、教师偏好和各种背景变量时,亲社会和反社会课堂行为独立于学业成绩的预测变量之外.然后,探索社会行为与学业行为或教师偏好显著相关,与学业成绩间接相关.
400多名六年级和七年级学生,11名教师参加研究.该研究涉及5个变量的测量,亲社会行为、反社会行为、学业行为、教师对学生的偏爱、学业成绩.其中亲社会行为有两个特征:合作、共享;反社会行为有两个特征:动手打架、违反纪律.这两种行为的测量采用由学生对其他同学的评价的方法,在各个特征被同学提名的百分率基础上,每个学生得到一个亲社会行为综合分数和一个反社会行为综合分数.学业成绩用年级学年考试成绩和斯坦福基本技能测验的分数.学业行为由教师在一个5点量表上对下述行为给每个学生打分:①对学校作业的兴趣;②有独立工作能力;③关心评价.然后计算出每一个学生的学业行为得分.教师对学生的偏爱,采用教师评定方法,要求教师在一个5点量表上评价他们在多大程度上愿意让某位学生下半年仍留在他的班上.
在收集数据的基础上,通过计算相关系数,学业成绩与亲社会行为、学业行为、教师对学生的偏爱有显著正相关,与反社会行为有显著负相关.然后通过回归分析,求出路径系数,得到图3的模型(路径系数略):
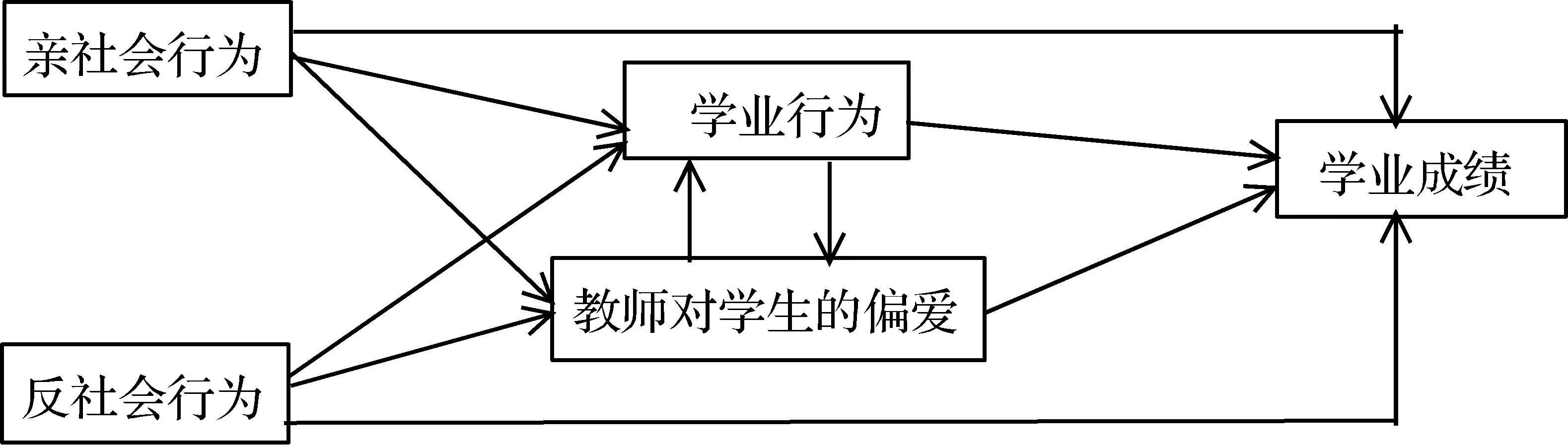
图3 五个变量之间关系的路径分析
3 路径系数的计算
3.1 一个实例的路径系数计算
假定我们要研究学生的成就归因、学习焦虑、学习倦怠、学业成绩四个因素之间的关系,依据学习理论的教学经验,构建一个如图4的路径分析模型.在这个模型中,成就归因是外生变量,学习焦虑、学习倦怠是内生变量,且为中介变量,学业成绩是因变量.
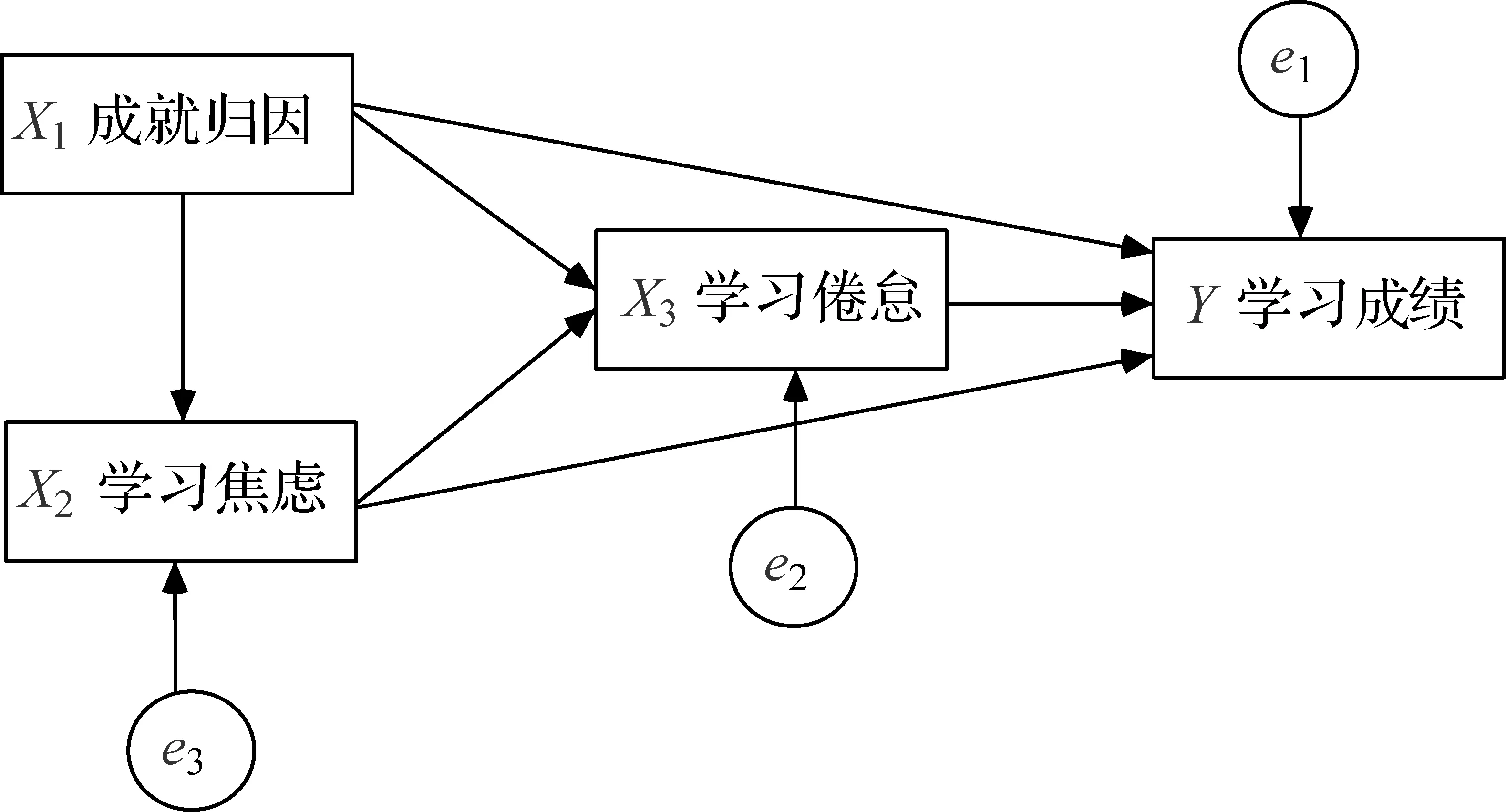
图4 学习中四个因素的路径图
用分别测量成就归因、学习焦虑、学习倦怠的三个量表对选定的被试进行测试,同时收集这组被试平时数次数学测验的分数,求平均分作为学生的学业成绩分数.
以上面的例子(原始数据略),用SPSS软件计算分为四步:求相关系数,方程1回归分析,方程2回归分析,方程3回归分析.
第一步,计算变量之间的相关.
(1)点击变量视图,定义四个变量:Y,X2,X1,X3.
(2)点击数据视图,输入数据.
(3)依次点击[分析]、[相关]、[双变量],得到<二元变量相关分析>主对话框.
(4)将对话框左边变量Y,X1,X2,X3调入右边下的<变量>矩形框内.
(5)选择Pearson,点击[确定].
结果见表1:
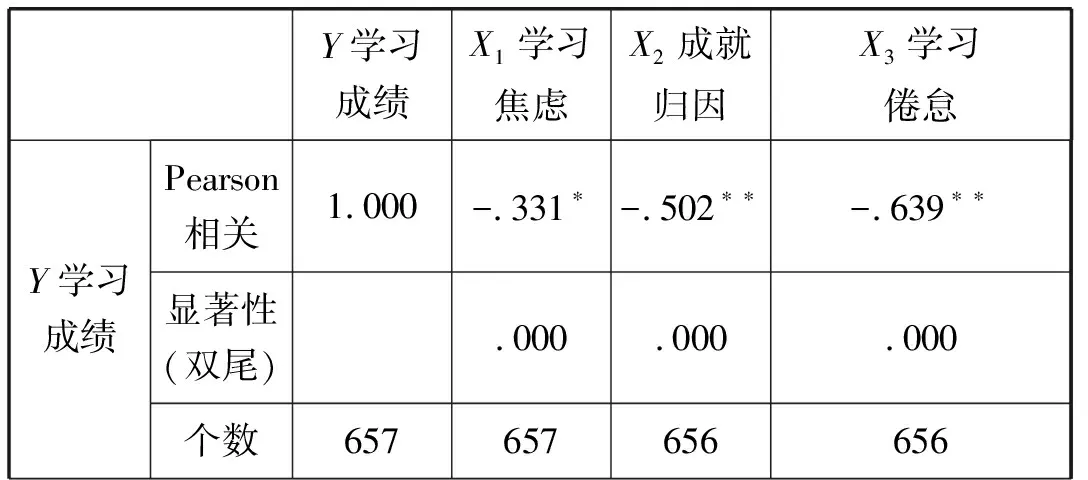
表1 变量之间的相关
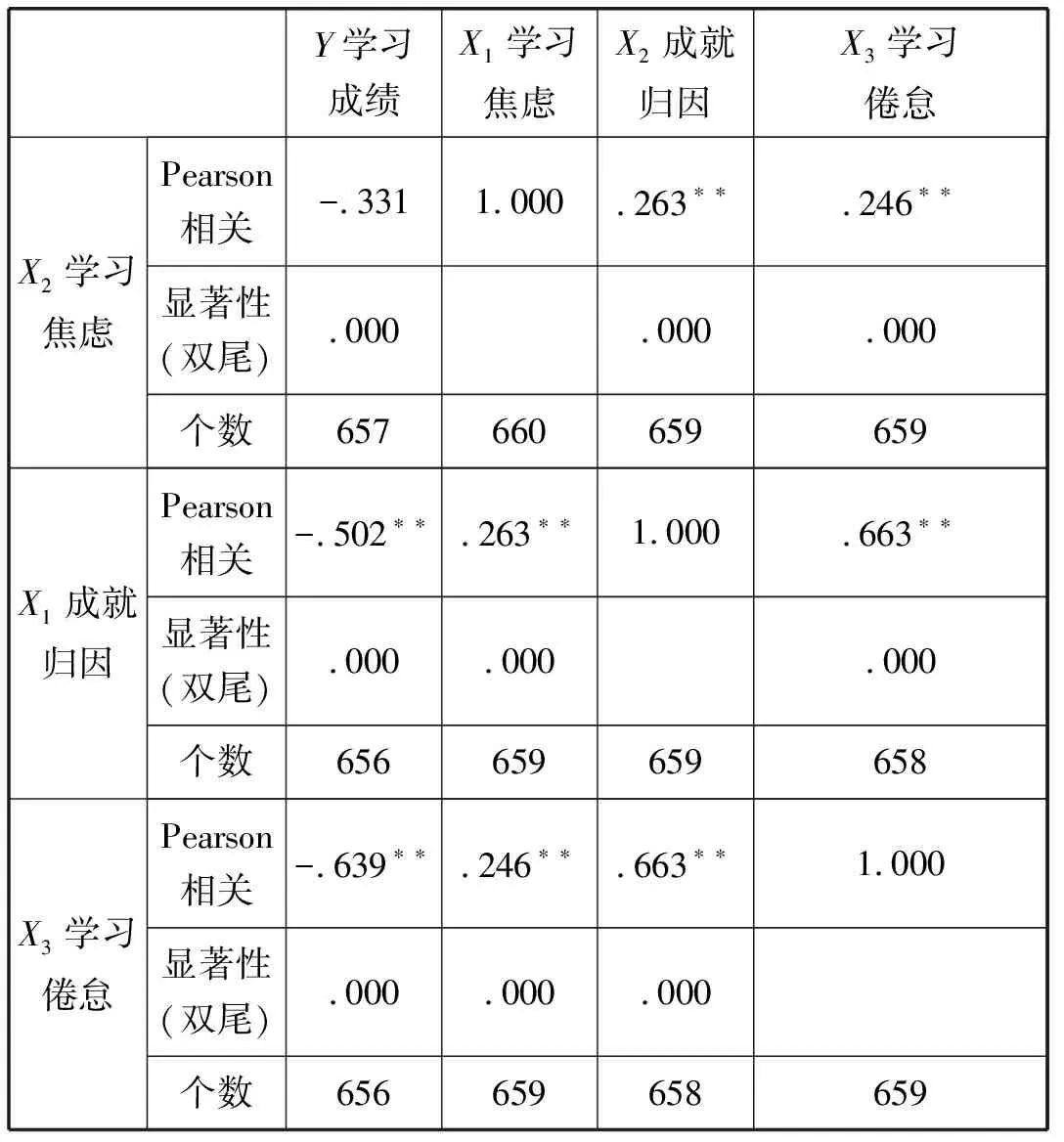
续表
第二步,方程1的回归分析.方程1:Y=β1YX1+β2YX2+β3YX3.
(1)点击[变量视图],将因变量“学习成绩”定义为Y.将三个自变量“成就归因”、“学习焦虑”、“学习倦怠”依次定义为X1、X2、X3.
(2)点击[数据视图],输入数据.
(3)依次单击[分析]、[回归]、[线性],弹出对话框.将左边源变量Y送入 <因变量>小框中,将X1、X2、X3送入<自变量>小框中.
(4)单击[确定].
(5)选择重要因素,重新建立回归模型.点击[方法],选择<逐步回归>,点击[确定].
结果见表2:
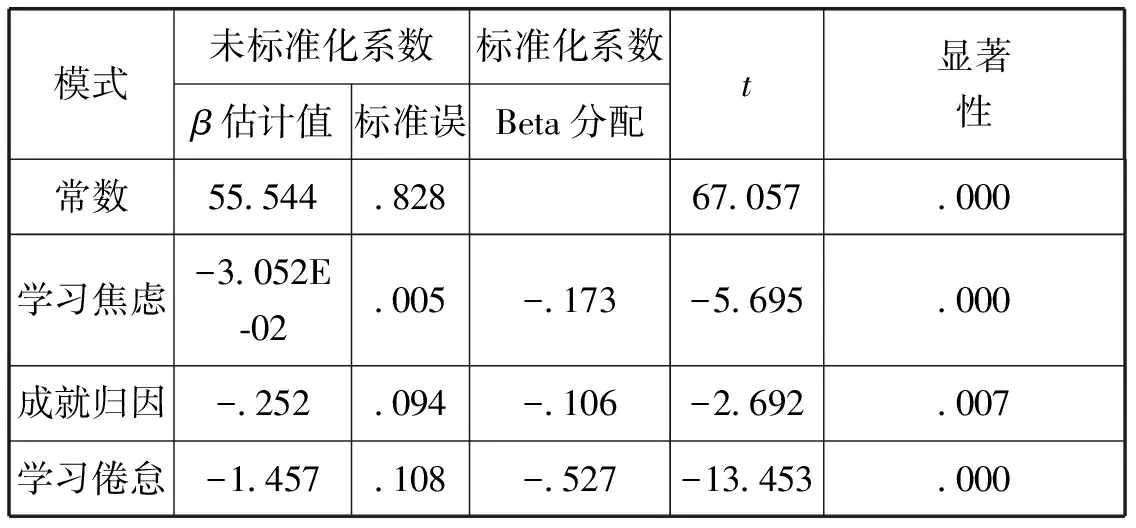
表2 方程1系数a
第三步,方程2回归分析.方程2:X3=β13X1+β23X2.
(1)点击[变量视图],将因变量“学习倦怠”定义为X3.将自变量“成就归因”、“学习焦虑”定义为X1、X2.
(2)点击[数据视图],输入数据.
(3)依次单击[分析]、[回归]、[线性],弹出对话框.将左边源变量X3送入 <因变量>小框中,将X1、X2送入<自变量>小框中.
(4)单击[确定].
(5)选择重要因素,重新建立回归模型.点击[方法],选择<逐步回归>,点击[确定].
结果见表3:
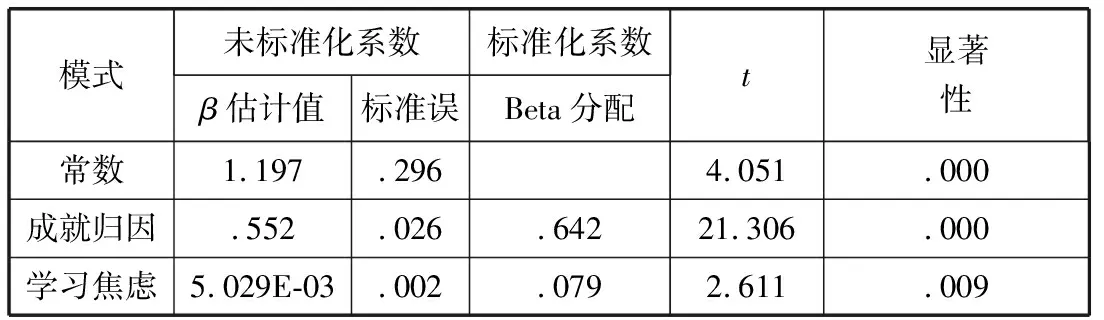
表3 方程2系数a
第四步,方程3回归分析.方程3:X2=β12X1.
(1)点击[变量视图],将因变量“学习焦虑”定义为X2.将自变量“成就归因”定义为X1.
(2)点击[数据视图],输入数据.
(3)依次单击[分析]、[回归]、[线性],弹出对话框.将左边源变量X2送入 <因变量>小框中,将X1送入<自变量>小框中.
(4)单击[确定].
结果见表4:
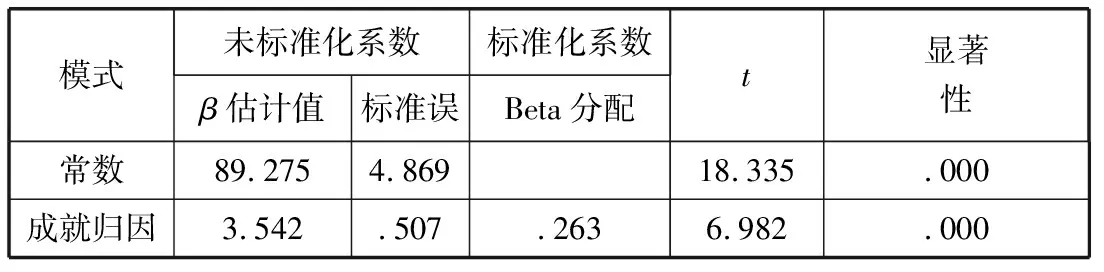
表4 方程3系数a
根据表2、表3、表4,标准化系数即为路径系数,可以得到路径分析的结果,见图5.
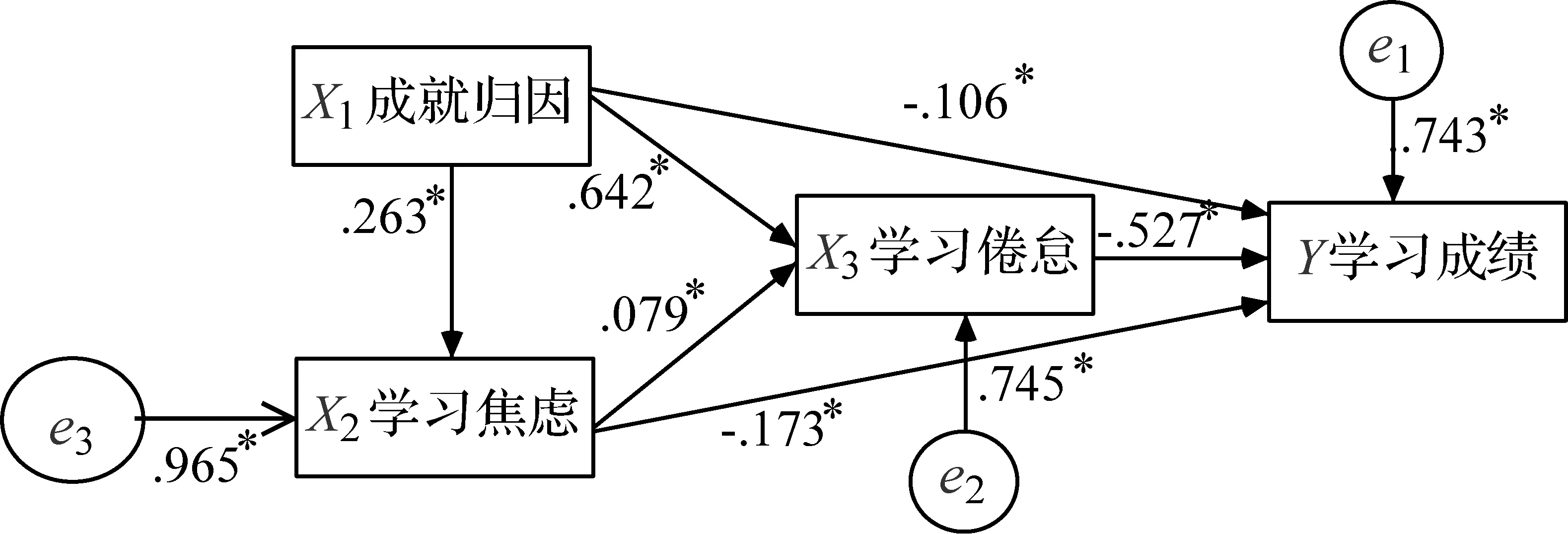
图5 路径分析结果
3.2 变量间的影响效果
(1)直接效果
直接效果是指直接从自变量到因变量间的效果,其路径系数即为直接效果的值.图3中,成就归因对学习成绩的直接效果是-0.106,学习焦虑对学习成绩的直接效果为-0.173.
(2)间接效果
自变量到因变量间,所有通过中间变量的效果,其效果的值为路径系数的乘积.间接效果为所有效果之和.
成就归因对学习成绩的间接效果有三种:
成就归因→学习倦怠→学习成绩:0.642×(-0.527)= -0.338;
成就归因→学习焦虑→学习倦怠→学习成绩:0.263×0.079×(-0.527)= -0.01;
成就归因→学习焦虑→学习成绩:0.263×(-0.173)= -0.045.
因此,间接效果=( -0.338)+ (-0.01)+ (-0.045)= -0.393.
(3)可能效果
自变量到因变量间的效果,如果两者均受另一共同变量的影响,其效果的值为路径系数的乘积.
学习倦怠至学习成绩的可能效果,其值为:0.079×(-0.173)= -0.01.
(4)变量间的相关系数的分解
自变量到因变量间的总效果即为两变量间的相关.总效果=总因果效果+所有可能效果;
总因果效果=直接效果 +所有间接效果.
