数学解题教学应让通解通法落地生根
2018-07-14卓斌
卓 斌
(江苏省宿迁市中小学教学研究室 223800)
1 问题的提出
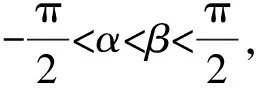
教师评讲时,首先指出学生没有认真审题,隐含条件α<β没有用到,因此答案错误.然后给出如下解法.
又因为2α-β=(α-β)+α,
课后交流时,笔者指出:按照您的思路,下面解法是否正确呢?
又因为2α-β=2(α-β)+β,
教师支吾不言!看来,解法一不但技巧性高,而且“有时候正确,有时候错误”.笔者进一步追问:您认为这是一道考查什么知识点的问题呢?有没有一般性的解法呢?他思索后恍然大悟,给出了下面的做法.
这次教学调研的经历让我深刻地认识到在数学解题教学中,一是要把握问题的数学本质,不能被表面现象所蒙蔽;二是要运用通解通法,避免繁难的解题技巧.一句话,数学解题教学应让通解通法落地生根.
2 对于通解通法的理解
章建跃先生曾批评当下解题教学的现状:搞“题型+技巧”,不重视“通性通法”,机械模仿多,独立思考少,数学思维层次不高.有些解法“不自然”,强加于人,对于学生数学学习兴趣与内部动机都有不利影响.章先生对于解题教学的看法可谓一针见血、入木三分.
史宁中先生在他的专著《数学思想概论》第3辑《数学中的演绎推理》一书旁注中指出:“求解个案问题表现的是技巧,而得到规律性表现的是技能.数学教育需要培养技巧,但是更重要的是培养技能”.并举例说明,在韦达(F.Viete,1540—1603)之前,人们还是个案地求解一元二次方程,后来韦达发现了一元二次方程根与系数的关系,才给出了一般性的公式,即求解一元二次方程的通解通法.由此可见,史先生也是大力倡导数学教育要注重培养解决一类问题规律性的技能,即通解通法.
在数学解题方面,以经历一般化加工的高考试题为例,其解题基本思路以及知识点都是学生已掌握的,但是在问题情境上因题目是从数值过渡到字母的表示,在思维观念上从正向思维变为逆向思维,因此常常让考生感到无从下手、无所适从.笔者认为数学解题的最高境界必然是“无招”.无招的背后,必然是有招,且招数的变化美妙了然于胸.无招的背后,必然是寻求以不变应万变的本质,而达到这样的境地,则必须熟悉复杂招数背后的本质.无招的背后,还是勤学苦练百次、万次的结晶,揣摩万千变化,才有可能接近无招胜有招的巅峰.数学解题中的“无招”,其实质应该是解题的“通解通法”.
那么,什么是数学解题中的“通解通法”呢?结合上述的观点,我们认为,通解通法就是解决这一类问题的最合理的想法、最基本的思路、最常用的方式、最普遍的操作程序.
笔者曾经辅导过几位数学后进生,他(她)们学习数学最大的障碍就是认为数学解题方法太灵活了,不难捉摸了,太难学会了.譬如,有的老师讲题喜欢一题多解,让他们有一种“雾里看花”的感觉,每一种方法都浅尝辄止,不得要领;还有老师讲题只讲怎么做,不讲为什么要这样做,以及怎么想到的这样做的,而且巩固训练也不到位,让他们呈现出“一看就会,一做就错”现象.实践表明,通解通法教学不仅有利于学生快速抓住数学知识的本质,形成有效解决问题的策略,而且有利于消除学生对数学学科的畏惧心理,增强学生学好数学的自信心.
3 例谈数学解题教学中的通解通法
3.1 分段函数问题,通解通法在于找准分段讨论的临界点.
对于自变量x的不同取值范围,有着不同的对应法则,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数.分段函数的定义域是各段函数定义域的并集,值域也是各段函数值域的并集.顾名思义,解决分段函数问题关键在于“分段”,通解通法就是找准分段讨论的临界点.
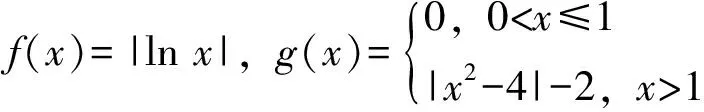
本题脱掉绝对值符号的关键点有两处,一是lnx的正负号,临界点是x与1的大小关系;二是x2-4的正负号,临界点是x与2的大小关系.又因为隐含了x>0的条件,所以需要分成三段进行讨论,即0
令h(x)=lnx+2-x2,
可知f(x)+g(x)的极小值为
f(2)+g(2)=ln 2-2<-1.
结合图象可知,
函数y=|f(x)+g(x)|与y=1的图象交点个数为4个.
所以方程|f(x)+g(x)|=1实根的个数为4.
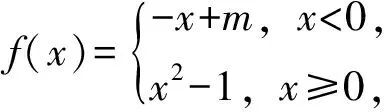
解析本题主要考查分段函数与复合函数的概念,以及函数零点等知识点,考查学生利用数形结合与分类讨论的数学思想方法解决复杂函数的能力.
本题处理复合函数y=f(f(x))-1关键点是利用x<0与x≥0的解析式,由于x2-1≥0取决于是否x≥1,因此临界点是x=0与x=1,所以需分三种情况进行讨论:
(1)当x≥1时,因为f(x)≥0,
所以f(f(x))=[f(x)]2-1=1,
(2)当0≤x<1时,因为f(x)<0,
EFpdepth,j为j类土地的足迹深度,EFpdepth,reg为区域内各种土地利用类型所组成的生态足迹广度。
所以f(f(x))=-f(x)+m=1,
解得f(x)=m-1.
又因为m>0,m-1<0,
所以0 (3)当x<0时,因为f(x)=-x+m>0, 所以f(f(x))=(f(x))2-1=1, 综上可知,当且仅当0 函数y=f(f(x))-1有3个不同的零点, 运用基本不等式求解最值问题有三个条件缺一不可:一正,二定,三相等.其中的关键点就是配凑或构造出定值,利用“积定和最小”“和定积最大”求出最值.实际问题中遇到的难点大多是“多变量函数”问题,通用的做法就是运用消元法减少变量. 案例3(2016年江苏卷第14题)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanB·tanC的最小值是. 因为sinA=2sinBsinC,A=π-(B+C), 所以2sinBsinC=sinBcosC+cosBsinC. 两边同除以cosBcosC, 得2tanBtanC=tanB+tanC. 又因为tanA=-tan (B+C) 因为三角形ABC是锐角三角形, 所以tanA>0,tanB>0,tanC>0. 得tanBtanC-1>0. 设tanBtanC-1=t(t>0), 所以tanAtanBtanC的最小值是8. 平面向量基本定理表明,任意一个平面向量可以用不共线的两个非零向量来线性表示,而且这种表示是唯一的.这提醒我们解决平面向量问题的通解通法应该是选好一组不共线的基底向量,并运用它们表征其余向量. 图1 且E,F是AD上的两个三等分点, 当然,平面向量数量积问题的另一种通解通法就是通过建立平面直角坐标系,把数量积转化为坐标的运算. 图2 案例7(自编问题)已知|2a-b|≤3,则a·b的最小值为. 解析本题考查平面向量数量积的最值问题,通解通法就是回归数量积的定义:a·b=|a||b|·cosθ,利用|a·b|=||a||b|·cosθ|≤|a||b|,实现条件与解题目标的有效对接. 因为|2a-b|≤3, 平方得4a2+b2-4a·b≤9. 又因为4a2+b2≥4|a||b|≥-4a·b, 代入上式得-8a·b≤9, 案例8(2017届南通市高三二模第14题)已知对任意的x∈R,3a(sinx+cosx)+2bsin 2x≤3(a,b∈R)恒成立,则当a+b取得最小值时,a的值是. 解析本题主要考查含有双字母参数的一元二次不等式恒成立问题,考查学生转化与化归、分类讨论、数形结合等数学思想方法.解题的关键在于把握问题的数学本质,采取各个击破策略.本题是运用通解通法解决复杂数学难题的最典型案例. 则sin 2x=t2-1, 因此不等式2bt2+3at-2b-3≤0 恒成立, 令f(t)=2bt2+3at-2b-3. (1)当b=0时,f(t)=3at-3≤0恒成立, (2)当b>0时, 不等式2bt2+3at-2b-3≤0 恒成立, 由线性规划,易得a+b无最小值,舍去. (3)当b<0时, 由线性规划,(a+b)min=0,a=0. 令a+b=t与9a2+16b2+24b=0相切, 所以a+b=-2. 江苏省中小学教学研究室董林伟先生倡导学生要整理好自己的“工具箱”,熟知自己拥有哪些工具,精通每个工具的功能,掌握每个工具使用的注意事项.解题就是自身拥有工具的调动与使用.我们认为,在解题教学中让通解通法落地生根,就是要抓好以下四个关键词. 一直以来,数学课堂教学仅限于听课和纸笔练习,学生的口头表达能力重视不够,造成学生“心求通而意未得,口欲言而词不达”,无法及时再现所学的数学知识,从而影响对所学知识的理解.说数学,就是让学生用自己的语言描述所学的数学定义、定理、公式、法则,说出对所面临数学问题的条件与结论的理解,说出解题方法的选择,说出关键环节的突破与克服.实践表明越能流畅表达的学生,对所学知识越熟悉,也容易理解知识中的隐喻内容,容易形成自己独到、深刻的理解,快速找到解决问题的通解通法. 所谓做数学,就是扎扎实实地做题目.做题是数学学习的主要内容,也是促进学生数学理解的最直接途径.做题的过程要精力集中、书写规范、思路清晰,逻辑性强,讲究速度与精度,会做的题目能够拿到满分,练好做题“童子功”.教师要给予学生充足的做数学的时间与空间,发挥学生的主观能动性,让学生亲历亲为,体验解题过程中的酸甜苦辣,积累成功的经验,也汲取失败的教训.同时,教师在解题教学中要率先垂范,板书工整、解题完整,小处强调步骤与程序,大处归纳解决一类问题的通解通法. 变式练习是指对数学概念和数学问题进行不同角度、不同情景、不同设问的变换,凸显数学概念的本质与外延,突出数学问题的结构特征,揭示数学知识的内在联系,真正做到举一反三,举三而反一类.南师附中葛军先生提出的生长教育:即由1生2,由1生4,由1生n,就是对于变式练习的最好诠释.变式练习中变化的是题目,不变的是通解通法.因此,变式练习是帮助学生掌握一类数学问题通解通法的不二选择. 画思维导图是由东尼·巴赞所创,这是一种将放射性思考具体化的方法.画思维导图是一种全新的思维模式,能够帮助学生灵活地由一种思路转换到另一种思路,从一个意境进入到另一个意境,多方位地试探问题的解决方法,让思维过程具有很强的发散性与灵活性.譬如,面对一个陌生的数学问题,可以问问自己,这个问题的条件和结论是什么?能举出几个实例吗?与哪个熟悉问题结构上相似?还可以追问自己,问题的反面是什么?逆命题成立吗?更一般的问题是什么?等等.唯有如此,才能实现章建跃先生所极力倡导的解题教学三重境界:知其然;知其所以然;何由以知其所以然.唯有如此,才能让通解通法落地生根,以不变应万变.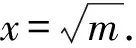
3.2 基本不等式问题,通解通法在于运用消元法减少变量.
3.3 平面向量问题,通解通法在于转化为基底表征方式.
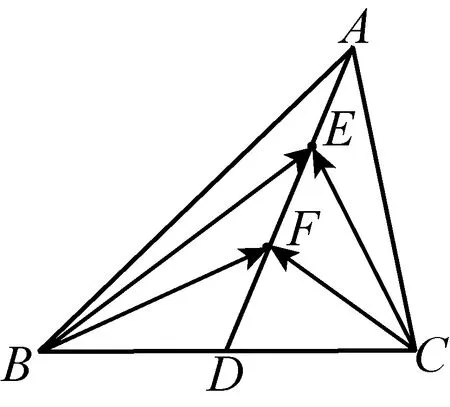
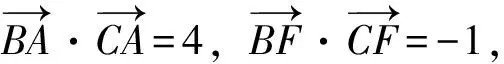
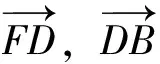
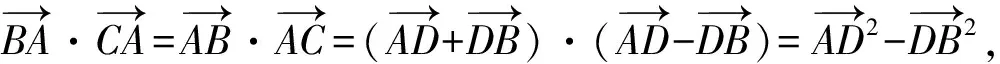
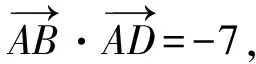
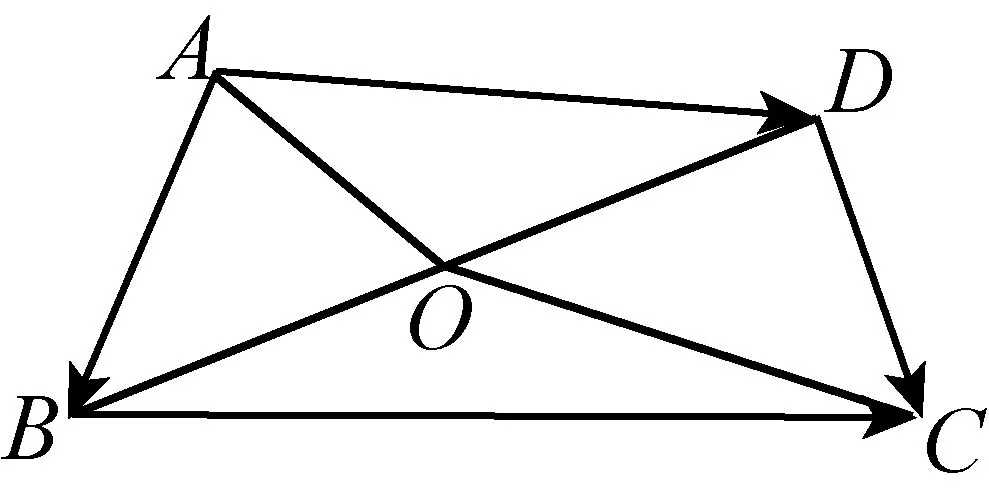

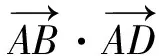
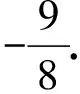
3.4 不等式恒成立问题,通解通法在于引进函数模型.
4 让通解通法落地生根的几点建议
4.1 说数学
4.2 做数学
4.3 变式练习
4.4 画思维导图
