核心素养渗透数学课程教学(续)

李尚志

(北京航空航天大学　100083)

五、字母运算：一次顶一万次

例4在如下空格中填入适当的数,使横向和竖向四个等式都成立：

分析这不是数学考试题,而是微信群中流传的智力测验.一般人想到的方法是猜一些数放进方格去计算,能够满足条件就是成功.比如,第一行两数之和等于8,你先填入 1+7=8试验.根据各列和 13,8算出第2行两个数 12, 1,但它们相减不等于 6,也不能再调整.这次试验就失败了.

第一行换成 2+6再试,第二行应为 11, 2,相减仍不等于 6.又失败了.

不断地试下去.试完了第一行的所有方案 1+7, 2+6, 3+5, 4+4, 5+ 3, 6+2, 7+1都失败.于是怀疑这个题无解.或者怀疑是动脑筋急转弯，就好比树上有 10只鸟,枪打掉 1只还剩几只,不但要算10-1,还要考虑听到枪声被吓跑了的鸟.

其实, 1+7, 2+6,…, 7+1并非第一行所有的方案.题目没有规定只能填正整数不能填分数小数,也没禁止负数、无理数、分数.把它们考虑进去,有无穷多种方案可以选择.你不可能全都去试一遍.

能不能只算一次就把所有的方案一网打尽,从中找出正确的方案？

当然可以!只要让第一行第一个数等于x,它就可以代表任何一个数.再算第一行第二数8-x,以及第二行两个数.只算一次就把所有的方案全部算了一遍.谁对谁错,全部一目了然.算一次还不只顶一万次,顶了无穷多次.所有的答案一网打尽.

解设第一行第一数为x.由第一行之和8得第二数为8-x.由两列之和 13，8得第二行第一数 13-x,第二数 8-(8-x)=x.再由两数之差 6得方程.很容易求出解.

(13-x)-x=6⟺13-2x=6⟺2x=13-6=7⟺x=3.5.

其余三个数依次为 8-x=4.5, 13-x=9.5,x=3.5.正确答案只有一个:

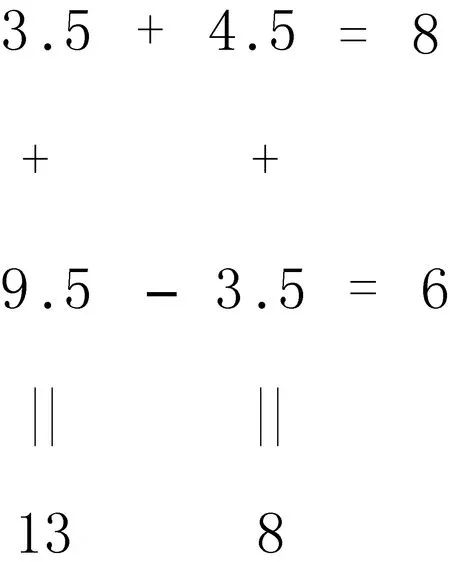
不难验证四个等式都成立.

本题没有要求用代数方法解答,也没有限定空格代表整数还是小数、分数、无理数还是虚数.唯一的要求是四个等式成立.你可以自己凑,凑出来就是成功.正如足球场上不管你是马拉多纳还是无名小卒,不管你用精彩动作还是难看动作踢进了球,只要没有犯规,同样都算一个进球.这是完全公平的.但是,你踢不进去，马拉多纳踢进去了,你还是输了.马拉多纳不是靠他的特殊身份赢球,而是与你公平竞争靠他的本事赢球,你不得不服.同样,本题你用算术方法凑不出答案,也没有想到答案不是整数而是小数.只要用代数方法设一个x,就把你凑过的和没凑过的方法一网打尽全部囊括进去了.你也不需要想到答案不是整数,只管按部就班地算,算出来是什么就是什么,是小数就是小数.不过你知道它不可能是无理数或虚数,因为你的已知数都是正整数,解一元一次方程只要用到加减乘除运算,得出的答案不能保证是整数,但一定是有理数.

很多书苦口婆心宣传字母代替数的好处.这里不用宣传.你不用字母做不出来,用了字母就做出来了,好处明摆着.字母的好处是：你愚公移山一锄一锄地挖山不止永远挖不完,字母运算是神仙下凡只做一次就全部般走了.你服不服?

其实本题也可以不用字母,只用算术方法也可以做：两列和 13+8=21是四个数之和.两行和与差 8,6之和 14,是三个数之和减去剩下一个 (右下角).二者之差 21-16=7是右下角的数的2倍,因此右下角为 7÷2=3.5.然后就容易算出其他三个数.不过,这个方法需要技巧,而字母运算只要按部就班就能算出来,就象傻瓜相机,专供不想动脑筋的人用.你喜欢哪个?

用字母运算囊括无穷多个具体的数值运算,就是用抽象囊括具体,是数学抽象核心素养的一宗利器,你必须掌握.

六、运算律是代数之母

数数推出整个算术,是算术之母.字母运算,一个字母代表无穷多不同的数,没法数数了,靠什么算？靠运算律.运算律是代数的公理,推出整个代数,不仅是中学代数或大学的高等代数,而是整个代数.由运算律推出代数,这门课程叫抽象代数.

运算律,包括我们小学就熟悉的交换律,结合律,分配律.还包括 0的定义,-a的定义.

我们最开始是由现实模型来认识 0和-a.零 0代表没有,代表不动. -a代表与a大小相同,方向相反.

对0和-a的抽象刻画是用运算律.抽象的好处是适用范围更宽:当 0不是代表没有,-a不是代表相反向量,只要运算律还成立,结论仍然成立.

0的定义:a+0=a对任何a成立.-a的定义:a+(-a)=0.

0a=0却不是公理而是定理:

由于减法是加法的逆运算,由a+0=a就得a-a=0.

由0a+0a=(0+0)a=0a知 (0a+0a)-0a=0,即 0a=0.

为什么负负得正？我们已经用旋转模型解释过.现在用逻辑推理解释:

由a+(-a)=0不但说明了-a是a的相反数,也说明了a是-a的相反数:a=-(-a).

对任意a,b有ab+(-a)b=[a+(-a)]b=0b=0,且 (-a)(-b)+(-a)b=(-a)[(-b)+b]=(-a)0=0,因此 (-a)(-b)与ab都是 (-a)b的相反数,因此它们相等:(-a)(-b)=-(-a)b=ab.

也可以用字母运算推理:x=-a,y=-b⟺x+a=0=y+b⟹xy=xy+a(y+b)=xy+ay+ab=(x+a)y+ab=0y+ab=ab.

由运算律可对任意a,b得完全平方公式 (a+b)2=a2+2ab+b2：

(a+b)(a+b)=a(a+b)+b(a+b)

=(aa+ab)+(ba+bb)(分配律)

=a2+(ab+ba)+b2(加法结合律)

=a2+(ab+ab)+b2=a2+2ab+b2(乘法交换律)

如果把a,b换成向量a,-b,加法由三角形法则定义,乘积ab换成向量内积a·(-b),以上三个运算律仍成立,推理过程仍然正确,结论仍然成立:

(a-b)2=a2+b2-2a·b.

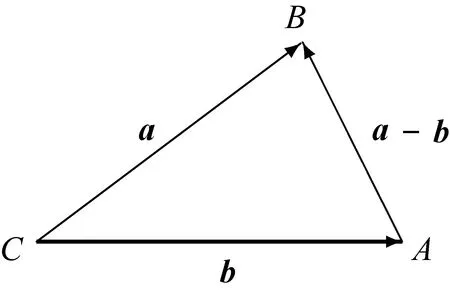
图3

当∠ACB=90°时a·b=0, |AB|2=|CB|2+|CA|2.就是勾股定理.

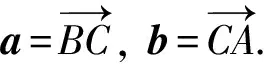
|BA|2=(a+b)·(a+b)

=(a+b)·a+(a+b)·b

(1)

=a·a+b·a+a·b+b·b

=|BC|2+|CA|2

(2)

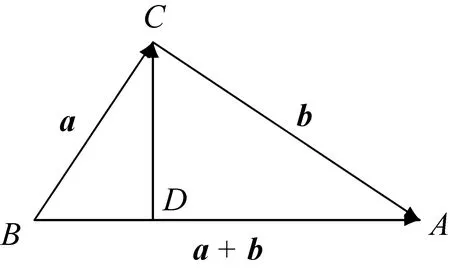
图4

试将以上向量运算过程翻译成勾股定理的一个几何证明.

分析将向量运算等式中的数量积改写为几何定义,变成

|BA|2=|BA||BC| cosB+|BA||CA| cosA

[1]

=|BC|2+|CA|2

[2]

向量等式 (1)就是展开式

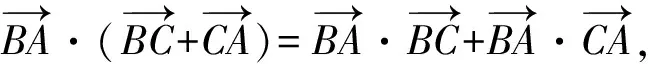
理由是点乘对加法的分配律.几何证明不承认这个理由,需要用几何方法将向量点乘分配律证明一遍.

证明作CD⊥BA交BA于D.则

|BA|2=|BA|(|BD|+|DA|)

=|BA||BD|+|BA||DA|

=|BA||BC|cosB+|BA||CA| cosA,

将|BA|cosB=|BC|,|BA|cosA=|BA|代入即得

|BA|2=|BC|2+|BA|2(勾股定理)

以上证明关键步骤

|BA||BD|=|BA||BC| cosB=|BC|2,

|BA||DA|=|BA||CA| cosA=|CA|2,

例5证法2作CD⊥BA,垂足为D.则

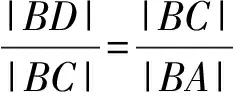
⟹|BA||BD|=|BC|2.

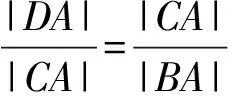
⟹|BA||DA|=|CA|2.

|BA|2=|BA|(|BD|+ |DA|)

=|BA||BD|+ |BA||DA|=|BC|2+|CA|2.

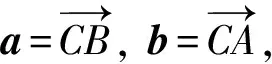
(a-b)·(a-b)=(a-b)·a+(a-b)·(-b)

=a·a+(-b)·a+a·(-b)+(-b)·(-b)

=a·a+b·b-2a·b.

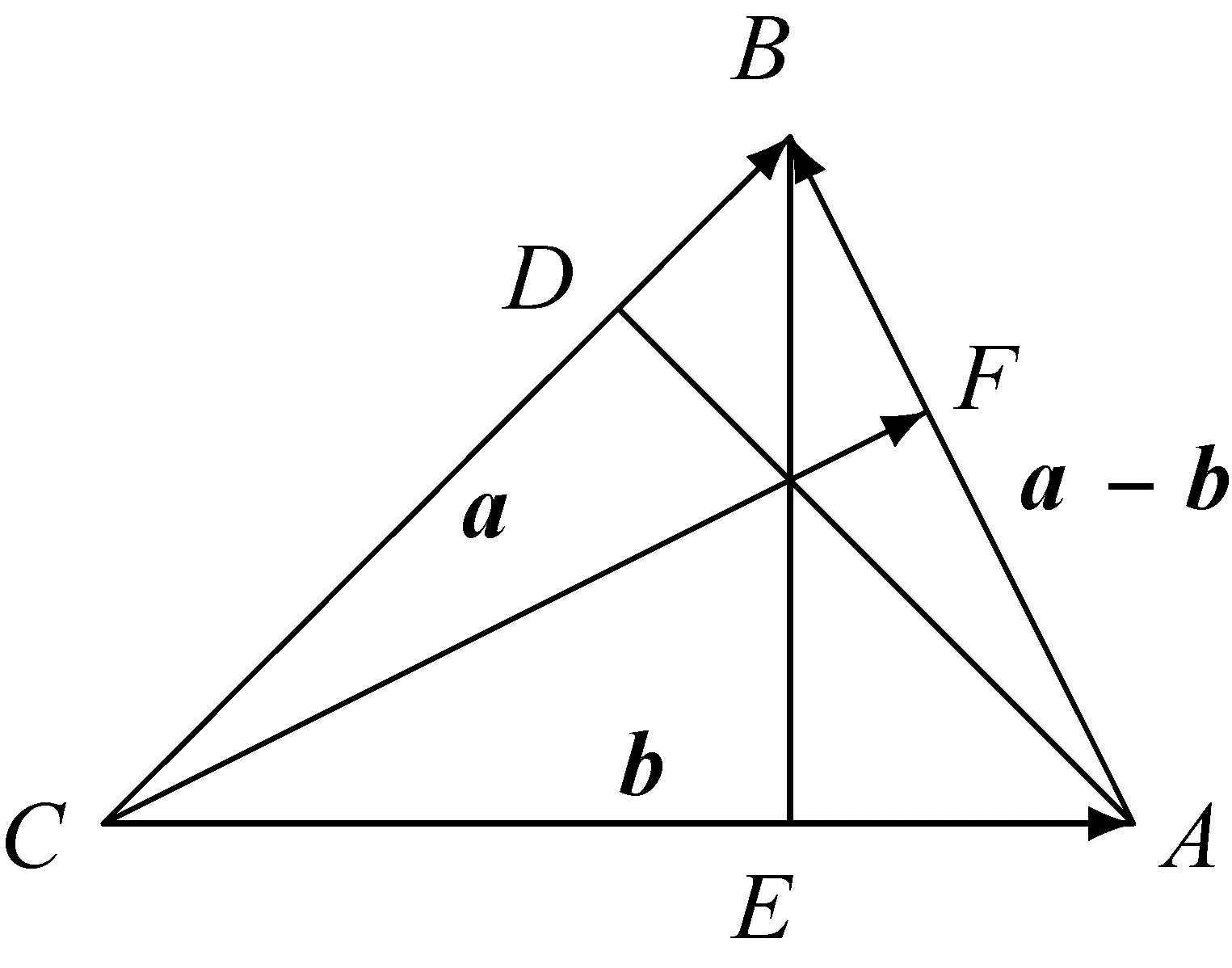
图5

证明作△ABC的三条高AD,BE,CF.则

|AB|2=AB·(AF+FB)=AB·AF+AB·FB

=|AB||AC| cos ∠CAB+|AB||CB| cos ∠ABC

=AC·AE+CB·DB

=AC· (AC-EC)+CB·(CB-CD)

=|CA|2-CA·CE+|CB|2-CB·CD

=|CA|2-|CA||CB| cos ∠ACB+|CB|2-

|CB||CA| cos ∠BCA

=|CA|2+|CB|2-2|CA||CB| cos ∠ACB.

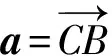
以上将向量运算翻译成几何证明,并非要求老师或学生掌握这种翻译方法,而是展示:向量运算律并非脱离几何另外诞生的新知识,而是某些几何定理改头换面变成的.利用运算律进行向量运算,得出几何定理,其实是由运算律所代表的简单几何定理推出更多的几何定理.

很多人认为:既然向量加法也叫加法,数乘、点乘也叫乘法,理所当然满足加法与乘法的运算律,不需再验证.另一方面,既然向量与数不同,运算定义也不同,数的运算律推出的公式就不能适用于向量,必须重新算过.

恰好相反,正因为向量与数不同,运算律是否成立必须利用几何知识重新验证.正因为向量与数有很多运算律相同,由这些运算律推出的公式就可以共同享用,不需要重新验证.

验证向量运算律并不难,费不了多大力气.验证之后的好处却很大:数的运算律所得出的结论全部可以直接应用,并且有新的意义.例如平方公式的几何意义是余弦定理和勾股定理.

向量验证了运算律之后,不仅可以享用这些运算律推出的已有结论,还可以贡献新的结论给满足同样运算律的其它运算系统享用.

例7对任意2n个实数a1,…,an,b1,…,bn,证明柯西不等式

等号成立仅当存在实数λ使bi=λai(∀1≤i≤n)成立,或所有ai=0.

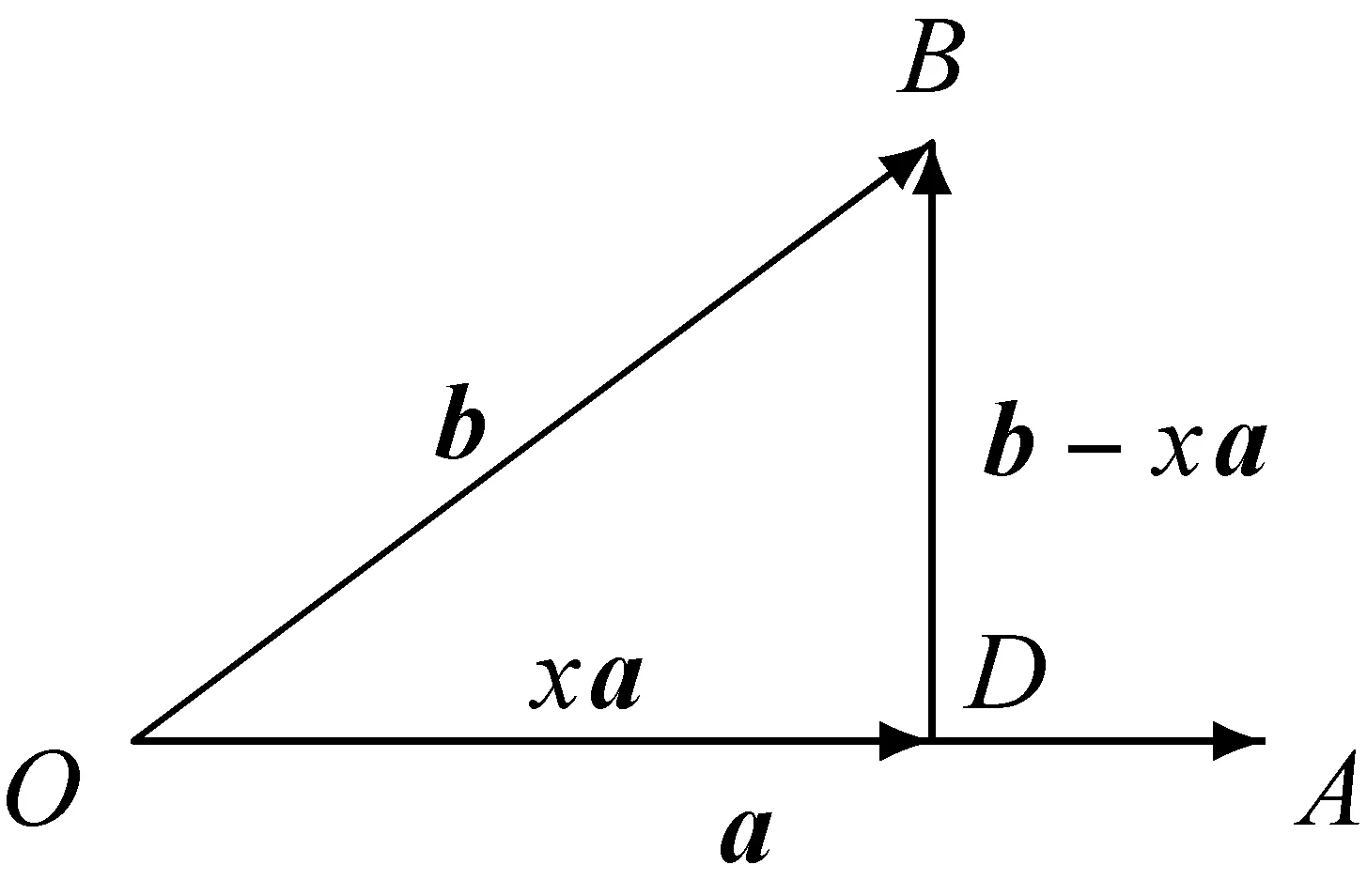
图6

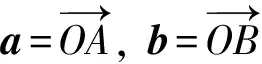
cos2∠AOB≤1得到

=|OA|2|OB|2

≥|OA|2|OB|2cos2∠AOB

=(a1b1+a2b2)2.

cos2∠AOB≤1这个几何理由也适用于n=3的情形,但不适用于n≥4的情形.当n≥4也可以定义向量a=(a1,…,an),b=(b1,…,bn),定义它们的加减法,数乘和数量积

a±b=(a1±b1,…,an±bn),

λa=(λa1,…,λan),

a·b=a1b1+…+anbn.

容易验证:这样定义的运算满足加法交换律和结合律,数乘和数量积满足对加法的分配律.因而可以推出完全平方公式(a+b)2=a2+2a·b+b2.并且在a⊥b时得到勾股定理 (a+b)2=a2+b2.

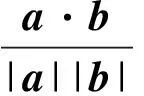
为什么几何方式定义的 |cos ∠AOB|≤1?因为它是直角三角形一条直角边与斜边之比,而直角边长度不超过斜边.为什么不超过?因为勾股定理,斜边长度平方等于两条直角边平方和,当然不能小于一条直角边的平方.

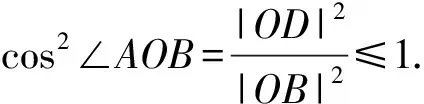
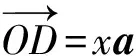
(xa)2+(b-xa)2

=x2a2+b2-2x(a·b)+x2a2

=2x(xa2-a·b)+b2

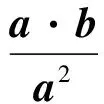
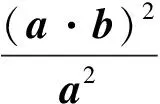
⟹a2b2≥ (a·b)2,

这就是柯西不等式.我们将以上论证翻译成不用向量语言的代数证明:

证明当a1=…=an=0时等号显然成立.

设a1,…,an不全为 0.则对任意实数x有不等式

以上不等式变成

(a1b1+…+anbn)2

等号仅当bi=xai(∀1≤i≤n)时成立.以上是按勾股定理 (xa)2+(b-xa)2=b2来选x.另一个选x的标准是使BD的长度 |b-xa|最短,也就是二次函数 (b-xa)2取最小值.

例7证法2当a1,…,an不全为 0时,有

f(x)=(b1-xa1)2+…+(bn-xan)2

=Ax2-2Cx+B≥0,

C=a1b1+…+anbn.配方:

以上证法2的理由是二次函数f(x)的最小值≥0.也就是说二次方程f(x)=0无实根或两实根相等,充分必要条件是判别式≤0.由此得到:

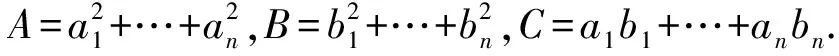
f(x)=(b1-xa1)2+…+(bn-xan)2

=Ax2-2Cx+B≥0,

抛物线y=f(x)在x轴上方,与x无公共点或只有一个公共点.方程f(x)=0无实根或两个实根相等,判别式

(-2C)2-4AB=4(C2-AB)≤0⟹AB≥C2

例7的三种证法都是针对具体实数ai,bi叙述的,但这些叙述都是在图 6的直角三角形的暗中指挥下写出来的.例5,例6正相反,是在向量算式指挥下写出几何证明.几何证明就得服从几何证明的规矩,不能把向量运算律照搬过去,但可以改头换面写成几何语言.代数证明则要遵照代数的规矩,把几何的想法改写成代数语言来叙述.这既是“他山之石可以攻玉”,也是“入乡随俗”.同样的道理,核心素养要指挥课堂教学,也必须入乡随俗,适应课堂教学的规律,随风潜入夜,润物细无声,才能发挥优势和威力,而不至于成为赵括的纸上谈兵.

例7的分析中选取实数x满足勾股定理 (xa)2+(b-xa)2=b2来证明柯西不等式a2b2≥(a·b)2的方法,既不依赖于几何图形,也不依赖于数值计算方法,只用运算律就推出了柯西不等式,既适用于几何向量,也适用于实数组.更进一步,不论你是什么集合V,只要在集合中任意两个元素a,b之间定义了加减法a±b,定义了集合元素a与实数λ的乘法,以及集合元素a,b的数量积a·b,满足我们熟悉的运算律,就满足由这些运算律推出的柯西不等式.

几何空间,数组空间都明确规定了其中的向量是什么,怎么做加减法,怎么做数乘和数量积,然后根据这些具体的规定验证运算律.它们都是具体的空间.具体空间虽然由不同的向量组成,运算的方式也不同,却有共同的运算律,都需要由运算律推出定理来使用.在不同空间中用同样的运算律进行同样的推理得到同样的结论,其实是重复劳动.于是它们共同成立一个服务公司,叫做抽象空间.把它们共同的运算律交给抽象空间去做共同的推理,推出的定理供各个具体空间共同享用.抽象空间不规定什么是向量,也不规定其中的向量怎样做加减法、数乘和数量积.抽象空间也不验证运算律,只规定加减法、数乘和数量积满足哪些运算律,专门负责由这些运算律推出各种结论供具体空间使用.为什么抽象空间中的运算律不需要验证而可以强行规定 ?运算律是否成立,为什么成立,是具体空间的任务.抽象空间只允许那些已经验证了运算律的具体空间称为向量空间,允许它们的运算称为加法、减法、数乘、数量积,只为它们服务.不满足运算律的集合和运算没有资格称为向量空间,运算也不能称为加法、减法、数乘、数量积.就好比厨师不负责种粮食、种菜和养猪,只负责把现成的米、面、肉类、蔬菜加工成美味的食品.(全文完)