体外预应力自复位框架拟静力试验研究
2018-07-14胡宇飞
鲁 亮 胡宇飞 刘 霞
(1.同济大学结构工程与防灾研究所,上海 200092; 2.东南大学城市工程科学技术研究院,南京 210096)
0 引 言
自从预应力技术出现以来,多数自复位结构采用预应力筋作为结构的地震恢复力装置[1-2],2012年和2016年吕西林[3-4]等分别进行了二维和三维摇摆钢筋混凝土框架模拟地震振动台试验研究,2014年鲁亮等[5-6]完成了受控摇摆式钢筋混凝土框架(Controlled Rocking Reinforced Concrete Frame,CR-RCF)的振动台试验研究。
现有研究的自复位结构的预应力筋均布置在梁柱构件体内,施工控制及后期监测有一定困难,在CR-RCF结构研究的基础上,鲁亮[7]等提出了体外预应力自复位框架(External Prestressing Self-centering Frame,EPSCF)结构,与体内预应力相比,体外预应力不会削弱构件截面积,预应力控制更加方便。EPSCF结构在柱脚节点和梁柱节点处均采用纯铰接连接,赋予了结构转动能力,从而弱化侧向刚度,减小了结构在地震作用下的加速度、层间剪力等响应。EPSCF结构上下层之间布置斜向对称的钢绞线来提供抗侧刚度,实现地震作用下结构的弹性自复位能力。同时,EPSCF结构设置了层间耗能装置耗散地震能量,减小位移响应,震后只需对耗能装置等进行必要更换,结构可很快恢复正常使用,符合“弹性可恢复”的抗震设计理念。
为了充分了解EPSCF结构的抗震特性,首先进行单榀单跨EPSCF结构拟静力试验,检验构造设计、模型简化、理论公式及有限元建模的正确性,并分析EPSCF结构的抗震性能。
1 试验方案
1.1 试验原型与相似关系
原型结构为三层EPSCF结构,层高3.6 m,横向柱距6 m,纵向柱距6 m,梁截面尺寸300 mm×500 mm,柱截面尺寸500 mm×500 mm。作为探索性试验研究,仅取单层单跨作为试验研究对象,如图1中虚线框。

图1 EPSCF结构简图(单位:mm)Fig.1 Layout of EPSCF structure (Unit:mm)
试验模型长度相似比取1/2,混凝土材料采用C40细石混凝土,纵筋为HRB400,箍筋为HPB300,预应力钢绞线型号为φs15.24。模型与原型的相似关系见表1。
表1试验相似关系

Table 1 Similarity of test
最终试验模型的装配图如图2所示。

图2 试验模型正视图(单位:mm)Fig.2 Front view of test model (Unit:mm)
1.2 梁柱节点与柱脚节点
梁柱铰接节点的构造如图3所示。柱顶预埋带预留孔的U形型钢,梁端预留与柱顶相同尺寸的开孔,钢插销分别穿过U形型钢及梁端预留孔,实现梁柱间的铰接连接。柱脚铰接节点的构造如图4所示。柱底和基础顶部均设计了带耳板的钢板预埋件,上下钢板预埋件通过配套的钢插销穿过耳板孔固定,实现柱脚的铰接连接。
1.3 预应力装置
1.3.1钢绞线的安装与调节
体外预应力钢绞线在框架内呈倒“八”字形对称布置,钢绞线上下两端均锚固于钢插销端部,上下钢插销分别插入混凝土梁内及基础预埋钢板的耳板中,如图4所示。安装时钢绞线依次穿过上下钢插销中预留孔,下端安装锚板,上端依次安装压力传感器、张拉调节装置及锚板。

图3 EPSCF结构节点Fig.3 Joints of EPSCF
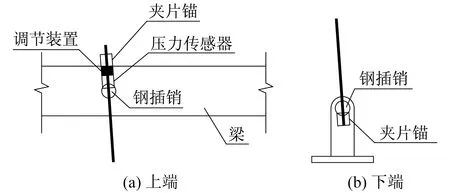
图4 体外预应力钢绞线锚固Fig.4 Anchorage of external prestressing steel strand
1.3.2钢绞线的初始张拉力与选型
图5为一榀单层EPSCF结构的分析模型,在侧向力F作用下,框架梁侧移Δ,层间位移角θ,左右两根钢绞线转动的角度分别为β和β′。根据几何关系和静力平衡条件推导的侧向刚度(式(1))[8],式中符号均为结构几何参数和预应力筋力学参数。
(1)
式中:H为层高度;L为框架净跨;d为预应力筋上下端锚固点间的相对水平距离;α为预应力筋与柱的初始夹角;F1,F2分别为预应力筋的内力。
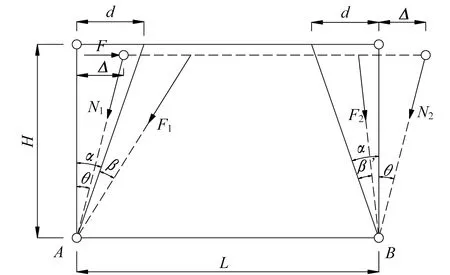
图5 EPSCF结构分析模型Fig.5 Analytical model of EPSCF structure
根据钢绞线摇摆过程中的最大设计应力和结构的位移限值可确定钢绞线与竖向所形成的夹角。EPSCF结构属于一种新型抗震结构体系,参考基于位移的抗震设计方法所给出的性能参数,确定EPSCF结构层间位移角限值[θ]≤1/20[9],即试验模型的最大水平位移为±90 mm。根据《混凝土结构设计规范》(GB 50010—2010)的规定[10],钢绞线的张拉控制应力不宜超过0.75fptk,fptk为预应力钢绞线的抗拉强度标准值。为了保证EPSCF结构始终处于弹性状态且钢绞线具有一定安全裕量,设定EPSCF结构所用钢绞线的最大拉应力为σe≤0.7fptk,取钢绞线的初始张拉应力σi=0.35fptk。由式(1)可求得钢绞线与柱的初始夹角α=0.069。
EPSCF结构侧向刚度由预应力筋提供,通过试算,抗侧向刚度为0.289 kN/m,单侧钢绞线为2根φs15.24标准型钢绞线,总截面积为A=280 mm2,抗拉强度标准值fptk=1 860 N/mm2,弹性模量E=1.95×105MPa。每根钢绞线的初始预拉力Fi=0.35×fptk×A=91.14 kN。
1.4 阻尼器
本试验采用一种轴向拉压型金属阻尼器作为耗能装置[11],阻尼器构造见图6。

图6 金属阻尼器构造Fig.6 Metallic damper
该阻尼器包括中心钢板、翼缘钢板以及耗能腹板,耗能腹板选用X形钢板,对称布置在中心钢板与翼缘钢板之间。阻尼器的一端连接在梁下焊接的耳板上,另一端与人字撑节点板相连。这种金属阻尼器构造方式的有益之处在于安装方便,同时阻尼器的变形不约束框架梁的竖向变形,地震作用下不会引起梁体的局部损伤。
1.5 加载制度和加载工况
试验所用加载设备为MAS-100型电液伺服加载系统,作动器最大出力100 kN、最大行程250 mm。梁端水平荷载采用位移控制方法施加,最大侧向位移为90mm,对应层间位移角为1/20。加载位移级差为30 mm以下每级增加5 mm,30 mm至90 mm每级增加10 mm,每级位移循环三周期。
加载工况包括无控和有控两种情况,这里的无控结构是指仅依靠钢绞线提供恢复力,而有控结构是在无控结构中增设阻尼器来增强结构的阻尼耗能能力。
拟静力试验方法为低周反复加载试验,重复进行了两组,每组试验包括两次有控结构试验和两次无控结构试验。在每次试验前对钢绞线预应力进行检查,对预应力松弛的钢绞线进行补张拉或更换钢绞线,保证每次试验前框架几何形状一致。每次有控结构试验后更换阻尼器再进行第二次试验。每次试验的加载制度完全相同。
安装完成后的有控结构试验模型如图7所示,拆除阻尼器后即可进行无控结构试验。

图7 有控EPSCF结构试验模型Fig.7 Test model of EPSCF with damper
1.6 传感器及测点布置
力传感器采用YBY-150型压力传感器,量程为150 kN,中间预留孔供钢绞线穿过,用于测量预应力钢绞线的初始力并全程记录钢绞线内力的变化。
位移传感器采用拉线式位移计,共布置2个,分别位于梁截面形心处以及基础中点处,用以测量框架水平侧移及基础侧向移动。
2 试验结果
2.1 阻尼器性能试验
分别对三组与试验尺寸相同的阻尼器进行拟静力试验,测试阻尼器的荷载-位移关系,为有限元模型中的阻尼器参数提供实测数据。试验时采用MAS-100型作动器加载,位移采用拉线式位移计测量,加载方式为位移控制加载,各级位移分别为30 mm、50 mm、70 mm、90 mm、100 mm,每级位移循环三周期。
以第一组阻尼器为例,试验得出的滞回曲线如图8所示。

图8 阻尼器滞回曲线Fig.8 Hysteresis curve of damper
对三组阻尼器实测结果取平均值后,得到的阻尼器的参数见表2,实测数据用于结构有限元计算。
表2阻尼器参数试验结果

Table 2 Test results of damper parameter
2.2 无控结构试验结果与分析
2.2.1荷载位移关系曲线
为便于描述钢绞线中的内力,对钢绞线进行编号,见图2,括号内为背面的钢绞线。
EPSCF无控结构中4根钢绞线的初始张拉力如表3所示,4根钢绞线的初始张拉力不完全相等,同侧钢绞线相差较小,不同侧钢绞线应力相差较大,与结构中的摩擦力共同作用达到受力平衡。
表3无控结构预应力钢绞线的初始预拉力
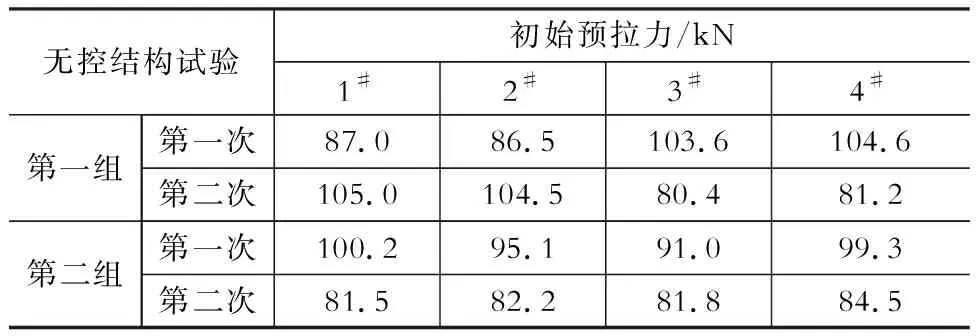
Table 3 Initial pretension of strands of EPSCF without damper
选取部分数据示例,试验得到的EPSCF无控结构的荷载位移曲线如图9所示,为方便比较,四组曲线按a、b、c、d依次编号。

图9 EPSCF无控结构荷载位移曲线Fig.9 Load-displacement curves of EPSCF without damper
由图中可以看出:
(1) 摩擦力的存在使结构的荷载位移滞回曲线具有一定的滞回面积,说明EPSCF无控结构具有一定的耗能能力,主要为摩擦阻尼耗能。
(2) 钢绞线初始张拉力的误差对结构耗能能力的影响不大。
2.2.2侧向刚度理论值与试验值对比
根据EPSCF无控结构第二组第二次试验绘制的骨架曲线如图10所示,利用骨架曲线求得结构的抗侧刚度为0.190 kN/m。由模型的实测尺寸代入式(1)计算得出结构的理论抗侧刚度为0.206 kN/m,实测值与理论值误差为7.8%。误差主要原因是理论公式计算假定所有梁柱、节点均为刚性体,而实际传力途径上构件、节点均有一定弹性及装配间隙。试验实测抗侧刚度与理论公式计算刚度的误差值在10%以内,证明了力学模型的合理性以及理论侧向刚度公式的正确性。
2.3 有控结构试验结果与分析
2.3.1荷载位移关系曲线
EPSCF有控结构4根预应力钢绞线的初始张拉力如表4所示。

图10 EPSCF无控结构骨架曲线Fig.10 Skeleton curves of EPSCF without damper
表4有控结构预应力钢绞线的初始张拉力

Table 4 Initial pretension of strands of EPSCF with damper
在试验过程中,4根钢绞线的最大荷载与抗拉荷载的比值均在0~0.7之间,说明钢绞线在摇摆过程中不出现松弛状态,同时留有充分的安全余量。以第二组第二次试验为例,压力传感器测得的4根钢绞线的总荷载与极限荷载比值如图11所示。

图11 钢绞线拉力变化图Fig.11 Tension variation of steel strands
EPSCF有控结构拟静力试验测得的部分荷载位移曲线如图12所示。
从图中可以看出:
(1) 4条荷载位移滞回曲线均十分饱满,对比图9所示无控结构的荷载位移滞回曲线,表明设置了阻尼器的EPSCF有控结构的耗能能力很强;
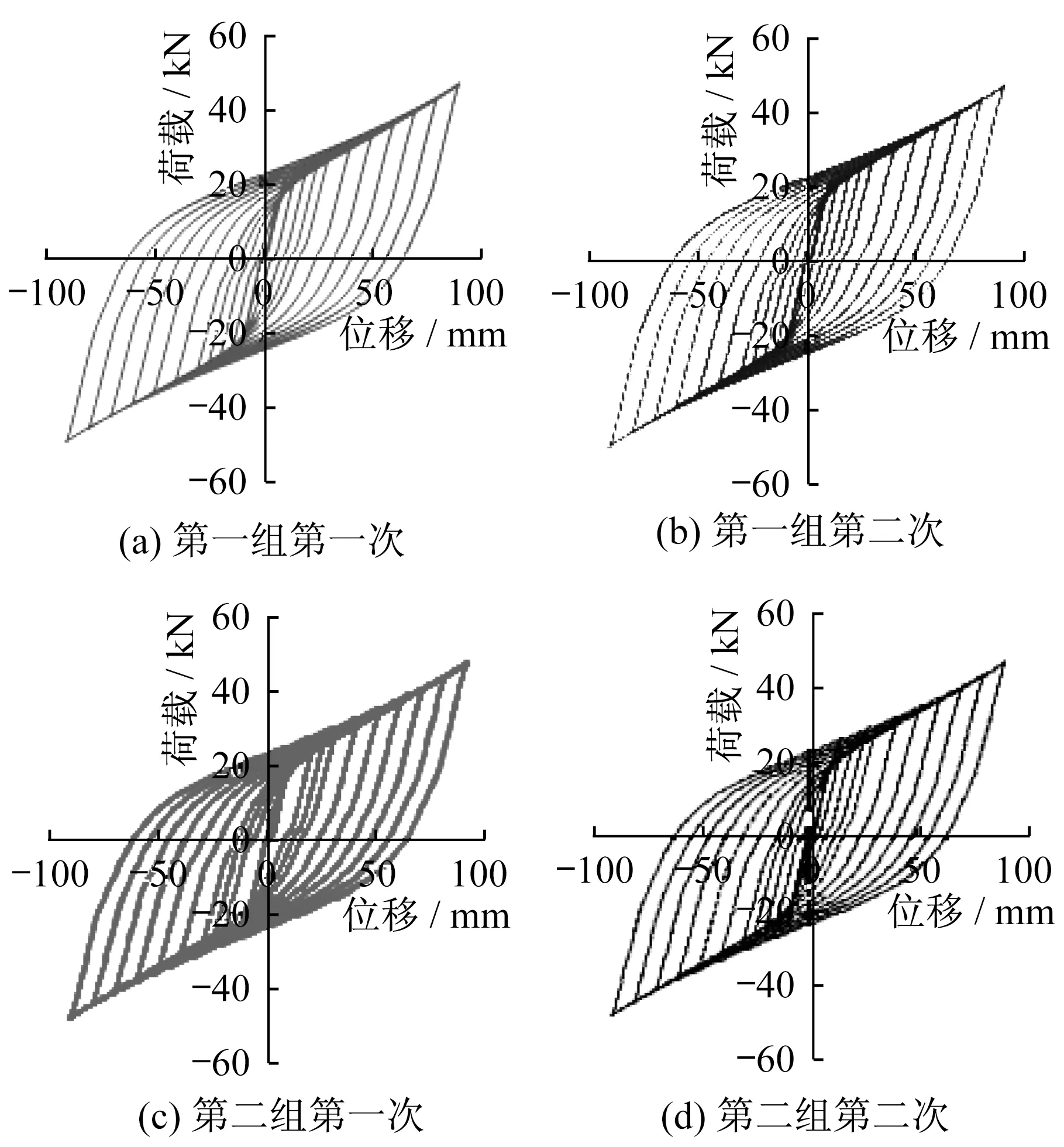
图12 EPSCF有控结构荷载位移曲线Fig.12 Load-displacement curves of EPSCF with damper
(2) 结构耗能能力与钢绞线初始预拉力差值无必然联系,不同钢绞线初始预拉力下所得到的试验结果几乎一致。
2.3.2骨架曲线
对EPSCF有控结构的四组荷载位移曲线取平均值,绘制有控结构的骨架曲线,并与无控结构的骨架曲线进行对比,如图13所示。
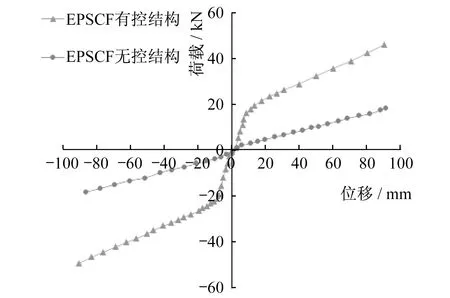
图13 EPSCF结构骨架曲线图Fig.13 Skeleton curves of EPSCF structure
从图13可以看出,由于阻尼器发生屈服,EPSCF有控结构荷载位移曲线上有明显的屈服点,而EPSCF无控结构几乎呈线性;同时,由于阻尼器本身有一定的刚度,EPSCF有控结构的屈服后刚度大于EPSCF无控结构的刚度。
2.3.3耗能特性
根据EPSCF有控结构和无控结构的滞回曲线计算的单圈能量耗散和等效阻尼比如表5所示,表中每个数据均为4次试验的平均值,每个位移下的单圈能量耗散值及等效阻尼比均取第2圈的试验数据。
表5能量耗散和等效阻尼系数
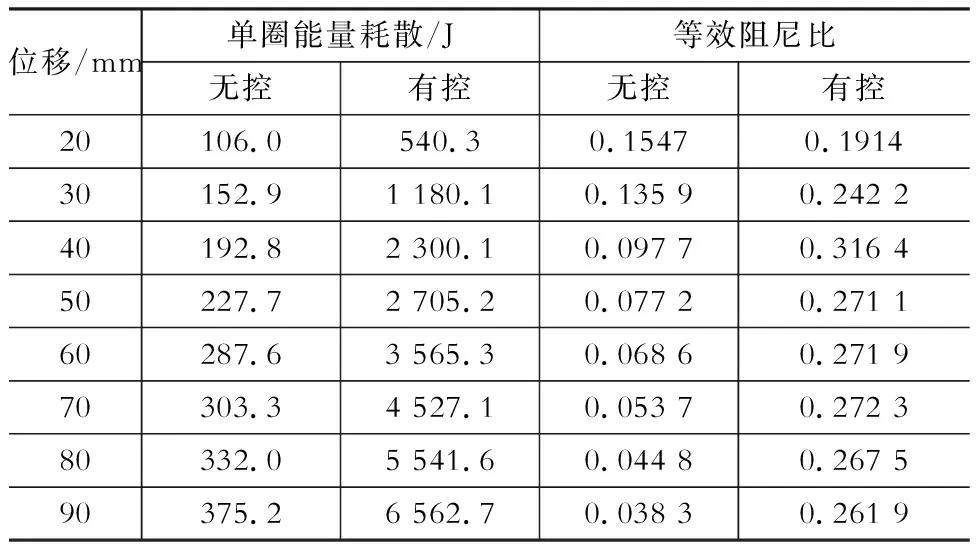
Table 5 Energy dissipating and equivalent damping coefficient
从表中可以看出:
(1) EPSCF无控结构的单圈能量耗散随位移增加而缓慢增大,90 mm位移时的单圈能量耗散仅为375.2 J。同时,无控结构的等效阻尼比随位移增加而迅速减小,20 mm位移时的等效阻尼比为0.154 7,90 mm位移时的等效阻尼比仅为0.038 3,减小了75%,说明构件间摩擦耗能占比随结构侧移增大而逐步减小,大位移下的无控EPSCF结构基本处于弹性工作状态。
(2) EPSCF有控结构在90 mm位移时的能量耗散为6 562.7 J,达到了EPSCF无控结构耗能的17倍。同时,等效阻尼比呈现先上升后略有下降的趋势,20 mm位移时的等效阻尼比为0.191 4,40 mm位移时的等效阻尼比达到最大,为0.316 4,之后略有平稳降低,90 mm位移时的等效阻尼比为0.261 9,说明设置阻尼器后,EPSCF结构的耗能能力显著提高。
3 有限元模拟
3.1 有限元模拟方法
采用ABAQUS软件对EPSCF结构进行建模计算,梁柱采用B31单元模拟,铰接节点采用连接单元Hinge模拟,预应力钢绞线采用Axial单元模拟,阻尼器采用连接单元Cartesian模拟。混凝土与钢筋本构采用基于ABAQUS开发的一组材料单轴滞回本构模型——TJ-Fiber[12]模拟。其中,阻尼器的恢复力模型由阻尼器性能试验得出,屈服位移和屈服荷载分别为12.19 mm和17.50 kN。
3.2 有限元模拟结果
有限元模型如图14所示,在梁端输入的位移值与试验值相等,将有限元计算得出的有控结构梁端荷载位移曲线与试验结果绘制于同一张图,如图15所示。从图中可以看出,有限元计算结果与试验结果吻合较好。
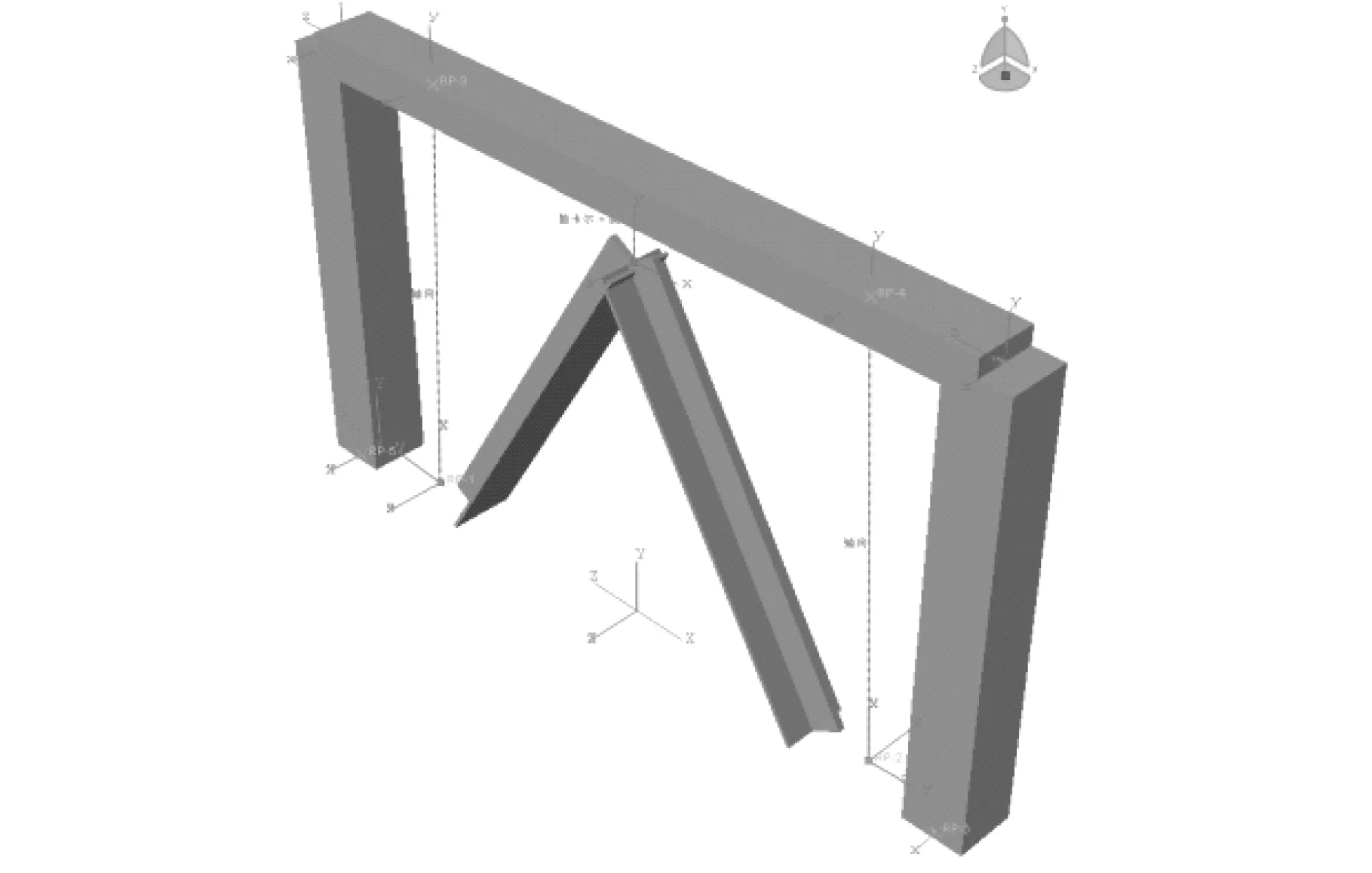
图14 EPSCF有控结构有限元模型Fig.14 Finite element model of EPSCF with damper

图15 EPSCF有控结构荷载位移曲线对比Fig.15 Comparison of load-displacement curves of EPSCF with damper between test and analysis
4 结 论
通过一榀单层单跨EPSCF结构模型的拟静力试验,了解了EPSCF结构的变形能力与耗能能力,得出以下结论:
(1) 由EPSCF无控结构试验实测的模型侧向刚度,与理论公式计算结果较一致,验证了理论侧向刚度公式的正确性。
(2) EPSCF有控结构的荷载位移滞回曲线饱满,对比EPSCF无控结构和有控结构的能量耗散和等效黏滞阻尼系数,表明设置层间阻尼器可显著提高结构的耗能能力。
(3) 有限元模拟结果与试验结果吻合较好,验证了有限元建模的正确性。
