黏滞阻尼器减震结构地震响应分析方法研究

贾传果 周 越 胡鹏飞

(1.山地城镇建设与新技术教育部重点实验室(重庆大学),重庆 400045; 2.重庆大学土木工程学院,重庆 400045)

0 引 言

结构耗能减震是通过在结构中设置耗能阻尼器,耗散输入结构的地震能量,从而减小结构的振动反应,减轻结构的损伤。合理的减震设计,可使强震作用下主体结构基本保持线弹性工作状态,而非线性状态主要集中在局部布置的若干耗能减震装置上,形成了典型的局部非线性问题[1]。耗能减震装置从其工作机理上可分为位移型阻尼器和速度型阻尼器[2]。本文研究主要针对速度型阻尼器,如黏滞阻尼器。

对于非线性黏滞阻尼器,其阻尼力模型一般表示为F=sgn(v)C·|v|α的形式[3](sgn(·)为符号函数,C为阻尼系数,α为阻尼指数),其中阻尼指数取值范围通常为0.1～1.0[4]。非线性阻尼器的优点在于其可以避免由于速度过大而导致的阻尼器超载现象,但较线性黏滞阻尼器,整体结构地震响应分析变得更为复杂[5]。

有文献[6]提出简化方法,通过估计非线性粘滞阻尼器的等效阻尼比,进行整体结构的地震响应分析。文献[7]基于估计的等效阻尼比计算阻尼减震因子,该方法已被写入FEMA450。这种方法给出的等效阻尼比与阻尼器的最大位移相关,故整体结构的地震响应分析仍需要迭代。事实上,等效阻尼比大多根据非线性阻尼器和线性阻尼器的能量消耗相等的原则确定的[8]。文献[9]通过数值模拟比较了模态阻尼法、半功率点法等规范以外计算等效阻尼比的方法。但文献[10]指出在阻尼比相同的条件下线性阻尼器减震结构与非线性阻尼器减震结构的地震响应有明显区别,这在一定程度上也说明采用等效阻尼比进行非线性阻尼器减震结构的地震响应分析存在一定的误差。

要提高精度,有必要对所得的局部非线性运动方法进行直接积分。传统的显式积分方法主要是针对非线性恢复力而言的[11]。对于安装有阻尼器的结构,非线性阻尼使得原本显式的积分方法不再是显式的,故求解时仍需迭代求解[12]。而对于隐式积分方法,非线性阻尼力需要更多的迭代步数,增加了计算量。对于非线性黏滞阻尼器,上述常规的显式或隐式积分方法可能出现严重的数值脉冲现象,从而导致时域分析方法的失稳现象[13]。

为避免迭代和提高计算稳定性,本文采用具有线性隐式特性的Rosenbrock积分方法。该方法主要有两个特点:一是需要计算每个积分步起始时刻的Jacobian矩阵;二是每个积分步均存在逆矩阵求解过程。这两个特点也是影响其计算量大小的关键因素。为此,本文对黏滞阻尼器的非线性数学模型进行线性化处理,并通过引入阻尼器方位矩阵,得到阻尼器减震结构的线性化运动方程。为进一步提高计算效率,本文在每一步积分过程中引入Sherman-Morrison求逆定理[13]简化逆矩阵求解过程。本文还对每个积分步的放大矩阵进行了谱分析,验证了该方法在求解非线性阻尼问题方面的稳定性。最终本文通过编制Matlab有限元程序对7层黏滞阻尼器减震结构进行地震响应分析,验证了该方法的计算效率和可靠性。

1 Rosenbrock积分方法简介

Rosenbrock积分方法是在隐式Runge-Kutta方法[14]基础上,采用内嵌牛顿迭代法实现显式化,被称为线性隐式方法[15],常用于一阶刚性系统初值问题的求解。Rosenbrock方法保持了Runge-Kutta方法的稳定性,同时避免了迭代。对于一阶非线性常微分方程,其初值问题可写为

(1)

将总计算时间等分为N个长度为△t的时间步长,记tk=k△t,yk为tk时刻的状态变量,应用二阶Rosenbrock法(2-stage L-stable Real Time Compatible method即LSRT2方法)[16]得出tk+1时刻的状态变量为

yk+1=yk+k2,

(2)

k1=(I-γΔtJ)-1f(yk,tk)Δt

(3)

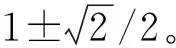
对于安装有阻尼器的结构,可以假定结构的恢复力为线性,阻尼力为非线性,其运动方程为

Ma(t)+C0v(t)+FD(v(t))+Kd(t)=P(t)

(4)

式中:M为质量矩阵;C0为结构固有阻尼矩阵;FD为非线性阻尼力向量;K为刚度矩阵;d为位移向量;v为速度向量;a为加速度向量;P为外界激励。

为采用LSRT2法,将二阶动力方程式(4)转化为一阶形式:

(5)

通过对无阻尼自由振动的分析计算,文献[9]对LSRT2方法进行了谱分析,给出了LSRT2法、Generalized-α法和Chang法的谱曲线对比图(图1),其中,ρ为普半径,Ω为数值频率(Ω=ωΔt)。由图1看出,LSRT2方法在整个Ω的取值范围内均小于等于1,高频区间(Nyquist frequency右侧)ρ随Ω的增大逐步趋近于0,低频区间(Nyquist frequency左侧)ρ随Ω的减小逐步趋近于1,说明LSRT2方法具备高频过滤特性,且能保证低频响应精度。文献[18]证明了Rosenbrock方法是能量衰减或保守的算法,这样的特性有利于其非线性稳定性[19]。

图1 LSRT2法的ρ-Ω关系曲线Fig.1 ρ-Ω curves of LSRT2 method

2 阻尼力模型线性化处理

为表述方便,假设阻尼指数为既约分数,即α=q/p,且q和p均为奇数,则阻尼力公式转化为F=C·vα。采用LSRT2法求解非线性问题时,每步均需求解当前步初始时刻的Jacobian矩阵。为简化积分过程,首先对阻尼力在tk时刻进行线性化处理,即对阻尼力在tk时刻按泰勒级数展开,并仅取线性项:

(6)

式中:vk为阻尼器tk时刻的相对位移。

令线性化后的阻尼系数为

(7)

则式(6)的阻尼力方程可以简化为

(8)

3 建立线性化运动方程

以平面框架模型为例,假设有m个自由节点,其位移和速度向量可表示为

d={x1,y1,β1,x2,…,xi,yi,βi,…,xm,ym,βm}

(9)

(10)

式中:xi,yi,βi为第i个结点的水平位移、竖向位移和转角位移。

假设有n个阻尼器,且均与结构在结点处铰接,其中第i个阻尼器的阻尼参数分别为Ci和αi,其与水平方向的夹角为θi。现引入阻尼器方位向量Li。如果阻尼器i一端与地面相连,一端与结点j相连,列向量Li的第3j-2个元素为cos(θi),第3j-1个元素为sin(θi),其余元素均为0,即

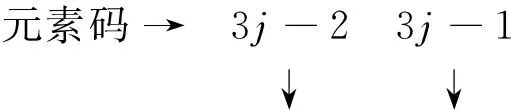
Li={0,…,cos(θi),sin(θi),0,…}T

文中所有上标T均表示矩阵或向量的转置。

如果阻尼器i一端与结点j相连,一端与结点k相连,那么列向量Li的第3j-2个元素为cos(θi),第3j-1个元素为sin(θi),第3k-2个元素为-cos(θi),第3k-1个元素为-sin(θi),其余元素为0,即

Li={…,cos(θi),sin(θi),…,

-cos(θi),-sin(θi),…}T

阻尼器i的轴向相对速度则可表示为

(11)

按公式(7)可得到阻尼器i的阻尼参数

(12)

式中:v(tk)为tk时刻的速度向量,后简写为vk。

按公式(8),可得到阻尼器i的附加阻尼力为

(13)

结构上阻尼器产生的阻尼力向量可以表示为

(14)

式中:A和D均为对角矩阵,

L矩阵是由每个阻尼器的方位列向量组成方位矩阵的转置,即

L={L1,L2,…,Li,…Ln}T

阻尼力向量左乘L矩阵的转置可得到所有节点所承受的阻尼力向量,

FD=LTF*=LTADLvk+LTDLv=

LTALPLTDLvk+LTDLv

(15)

式中:LP为矩阵LT的伪逆矩阵[12],若令W=LTALP,Ca=LTDL,式(15)可简化为

FD=WCavk+Cav

(16)

再代入结构运动方程(4)可得

Ma+(Ca+C0)v+Kd=P-WCavk

(17)

因此,对于一个含有相同类型阻尼器(阻尼系数C和阻尼指数α均相同)的结构,其运动方程就可以写为

(18)

4 改进Rosenbrock积分方法

对于线性化后的运动微分方程式(17),转化成一阶方程即为

(19)

其中,

应用LSRT2求解常微分方程式(17),则式(2)和式(3)的k1和k2可以表示为

(20)

k2=[I-γΔtJ]-1

(21)

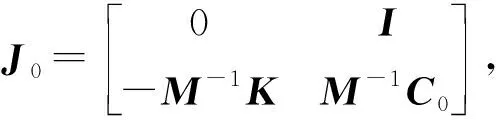
在式(20)和式(21)中存在矩阵求逆的过程。这是影响整个积分过程计算效率的关键。根据Sherman-Morrison定理[12],其中的逆矩阵求解可转化为

G=[I-γΔtJ]-1=[I-γΔtJ0-γΔtXDYT]-1=

H-γΔtHXBYTH

(22)

其中,H=[I-γΔtJ0]-1,B=[D-1-γΔtYTAX]-1。H矩阵可以在积分之前计算。因此,每个积分步中矩阵求逆只是计算B矩阵。B矩阵的维数与阻尼器的个数n相等。而G矩阵的维数与有限元的节点相关,大致为6m。一般情况下,阻尼器是局部布置的,故m≫n。原有Rosenbrock积分方法需要对一个6m维的矩阵求逆,而本文考虑Sherman-Morrison求逆定理后,只需要对一个n维矩阵求逆,理论上计算量得以大幅降低。

此外,由于非线性阻尼力模型的存在,原有Rosenbrock积分方法需要三次进行幂函数计算,即Jacobian矩阵更新、起点时刻f(yk,tk)和中点时刻f(yk+1/2,tk+1/2)计算。统一对线性化后的方程(17)进行积分,只需要一次幂函数计算,这也在一定程度上提高了计算效率。

5 稳定性分析

文献[17]对LSRT2方法求解无阻尼系统的稳定性进行了谱分析。改进的LSRT2方法每一步积分过程都是针对一个线性方程,但在线性化后运动方程的右边有一个项与初始时刻的速度相关。因此,本文采用谱分析方法对带有非线性阻尼力模型的单自由度系统进行分析。假设单自由度系统质量m=1 kg;刚度k=1 N/m;结构固有阻尼系数c0=0。图2和图3给出了当附加阻尼器的阻尼系数为0.1,不同阻尼指数对应的ρ-Ω关系曲线。

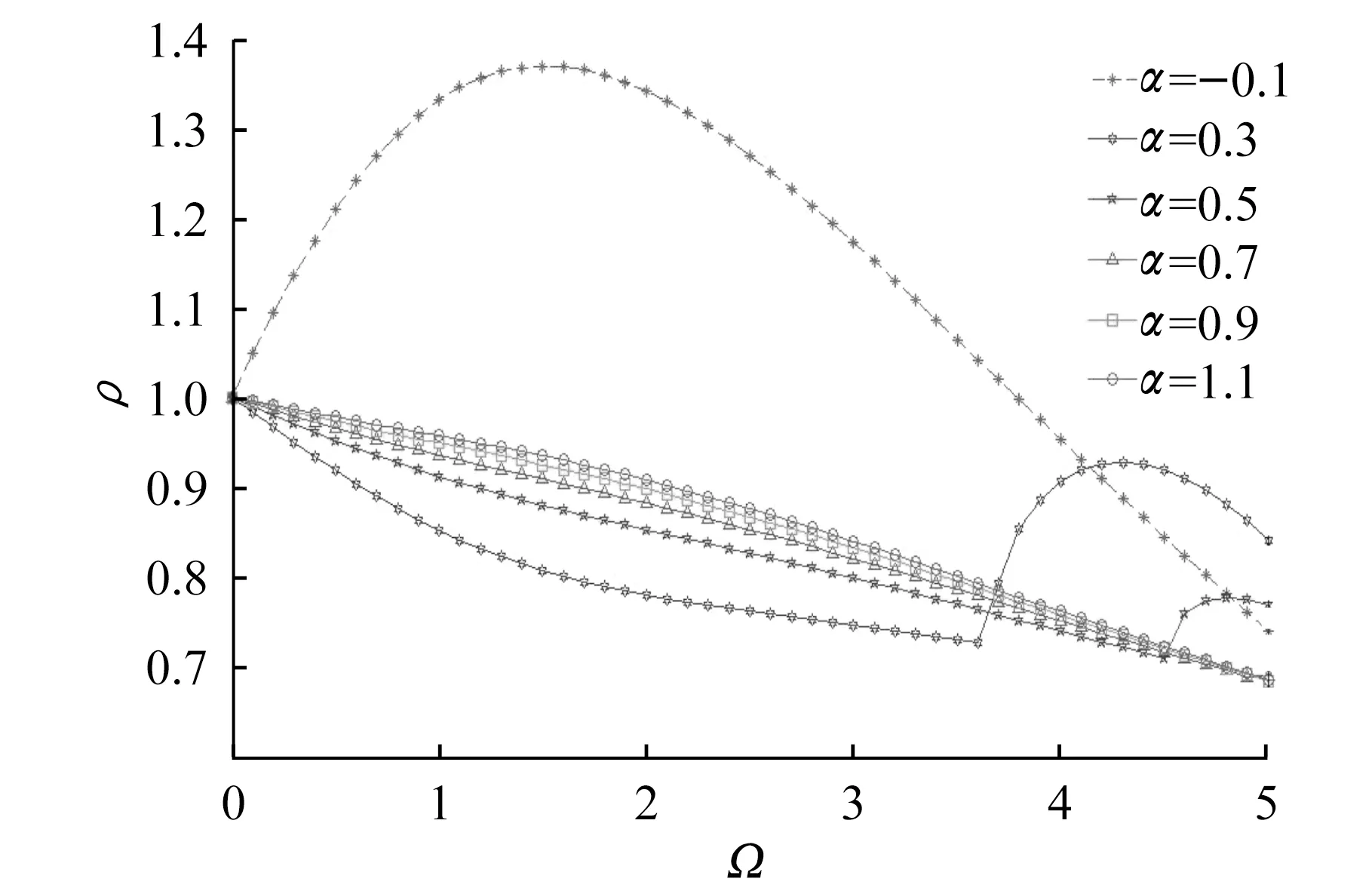
图2 LSRT2法求解非线性阻尼单自由度结构的ρ-Ω关系曲线Fig.2 ρ-Ω curves of LSRT2 for solving nonlinear damping single-DOF structures

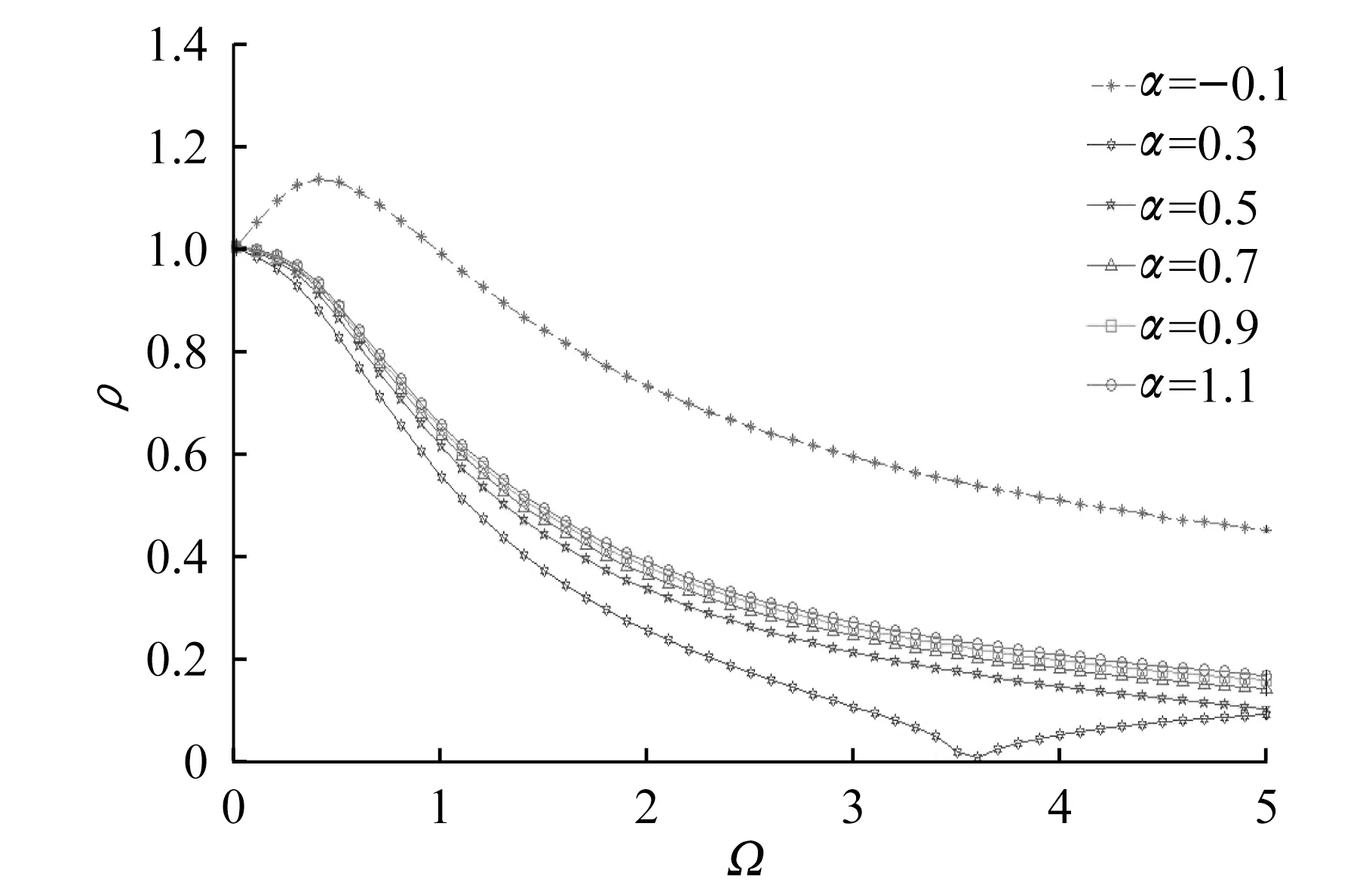
图3 LSRT2法求解非线性阻尼单自由度结构的ρ-Ω关系曲线LFig.3 ρ-Ω curves of LSRT2 for solving nonlinear damping single-DOF structures

从图2和图3可见,当阻尼指数α>0时,LSRT2法放大矩阵对应的谱半径ρ恒小于1;相反,当阻尼指数α<0时,在数值频率Ω数值较小时LSRT2法放大矩阵对应的谱半径ρ大于1,即其零稳定性[9]不满足。谱分析法给出的结论可以解释如下:当数值频率Ω数值较小时(即采用的积分步长较小时),公式(18)右边的速度相关项起到与左边类似的阻尼作用。若0<α<1,则起到正阻尼作用,公式(18)本身是稳定的。当α=1时,右侧速度相关项为0,公式(18)本身是稳定的线性运动方程。一般阻尼器,阻尼指数取值0<α≤1,但本文从数值分析角度,也对其他取值范围进行研究。若α>1,右侧速度相关项起到负阻尼作用,但公式(18)左边有正阻尼项,总体效果是正阻尼作用。总之,当α>0,非线性阻尼器起到正阻尼的效果,采用LSRT2求解是稳定的。反之,当α<0,采用LSRT2求解有失稳现象。

6 数值算例

基于以上计算过程,对一安装有非线性粘滞阻尼器的7层平面框架模型[20]进行数值模拟。结构为9度区7层钢筋混凝土框架结构,抗震等级为一级,Ⅱ类场地,结构立面图如图4所示。其中,每层高度为3.3 m,柱截面尺寸为500 mm×500 mm,梁截面为600 mm×300 mm。

现取一榀框架进行计算,二维框架结构采用平面刚架模型。阻尼器在结构中的位置如图4示,其阻尼力公式为F=1.8467v0.759 2。对于9度区,多遇地震加速度时程的最大值为0.14g。现采用El Centro波的x方向地震波对结构进行加载。整个计算过程(包括有限元建模和数值积分等)均在Matlab计算环境中完成。

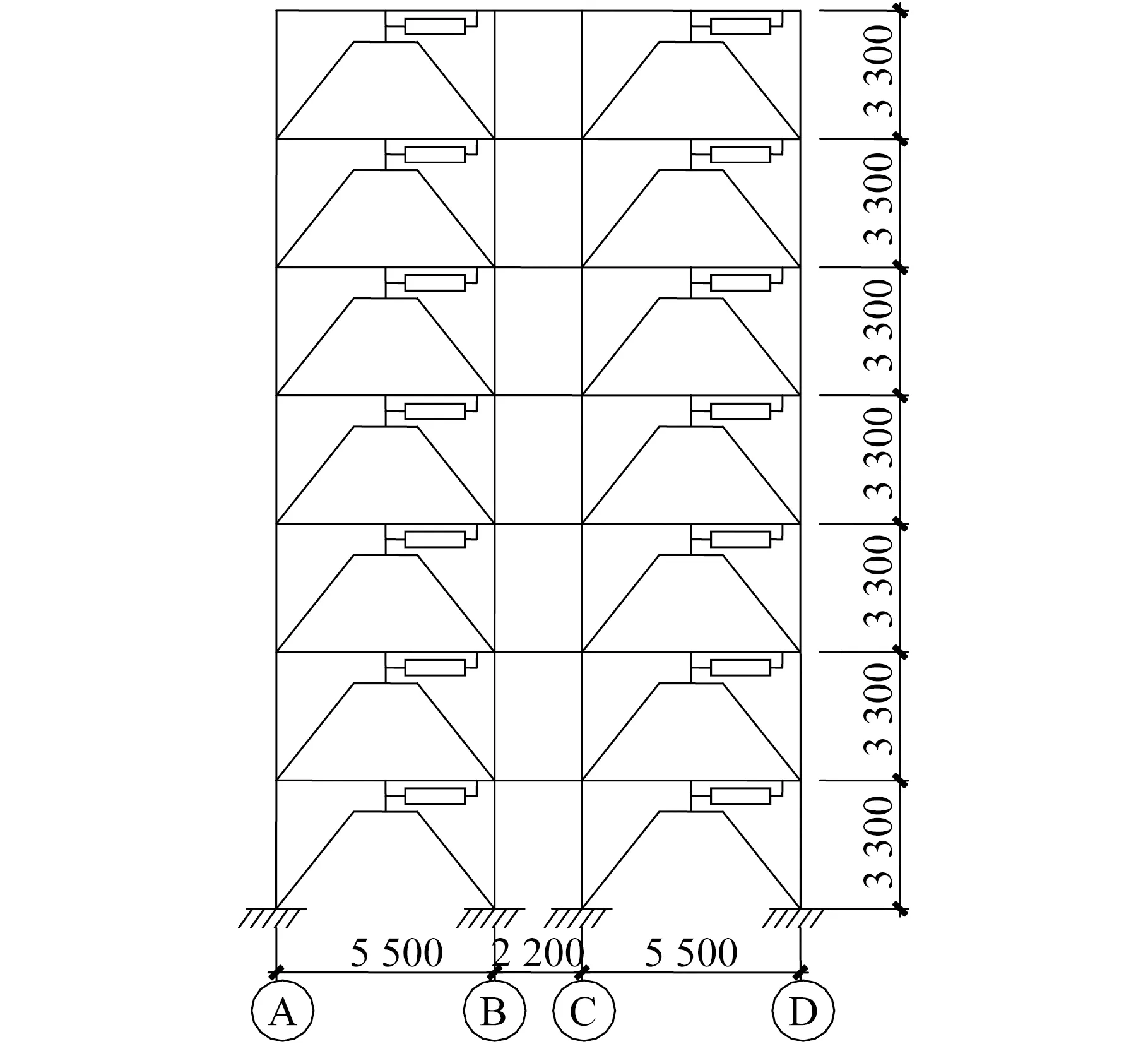
图4 结构立面尺寸及阻尼器布置示意图(单位:mm)Fig.4 The dimensions of the structure and the arrangement of the dampers (Unit:mm)

图5为多遇地震下结构的顶点位移时程曲线(前15 s)。从图5可以发现,采用改进前和改进后的LSRT2法计算所得的位移响应相近。但需要指出的是:采用LSRT2法,占用微机CPU的时间是28.314 2 s;而改进的LSRT2法占用CPU时间为8.546 8 s。因此,改进后计算效率大幅提高。

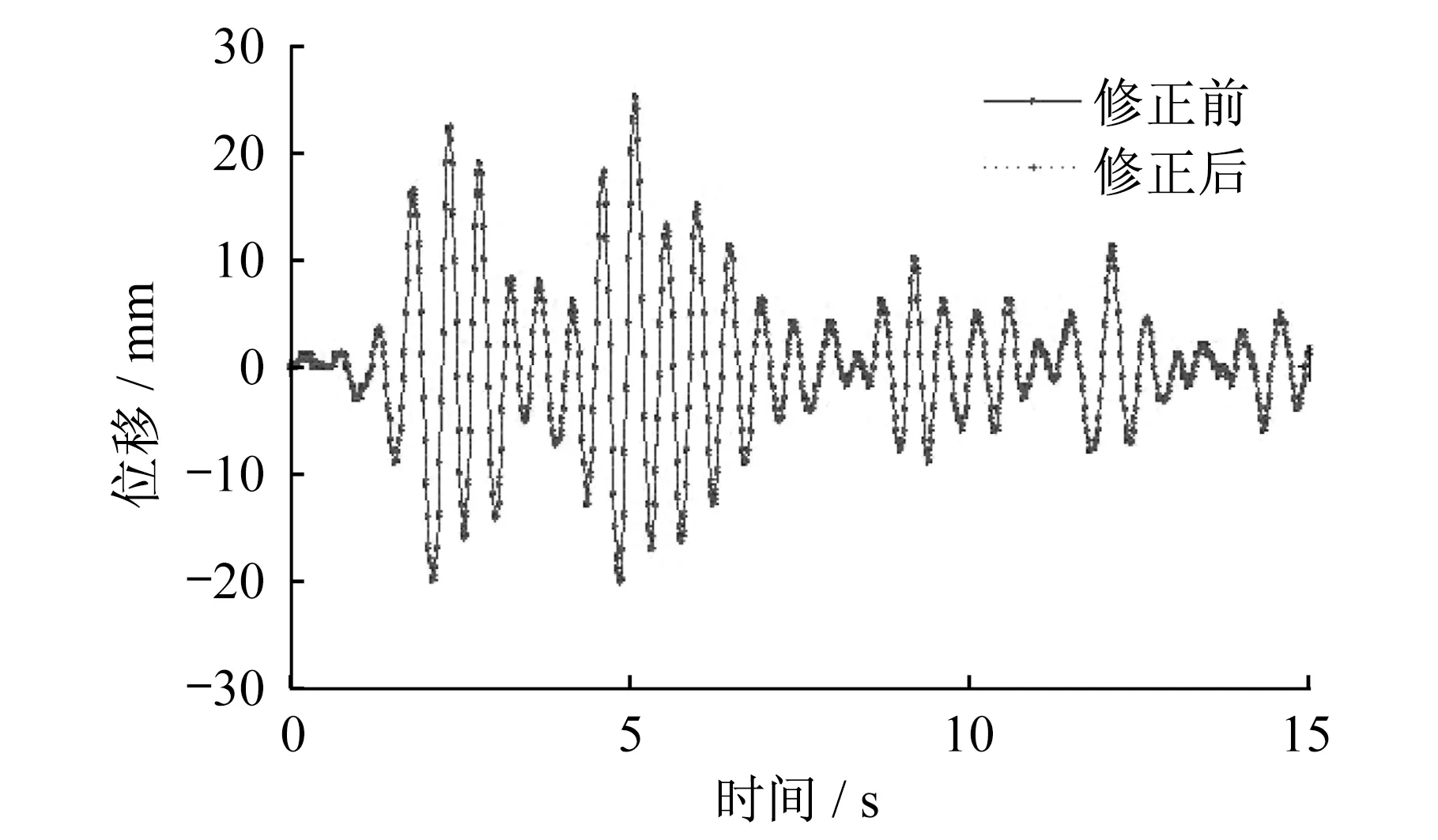
图5 地震作用下结构顶层位移时程曲线Fig.5 Displacement time-history curves of structure topunder the action of earthquake

7 结 论

黏滞阻尼器等减震装置一般局部设置在建筑结构的部分楼层,形成了典型的局部非线性问题。直接采用数值积分方法进行求解势必导致计算量大和计算程序复杂等问题。于此,本文基于线性隐式的Rosenbrock积分方法,提出黏滞阻尼器减震结构地震响应分析方法。具体结论如下:

(1) 针对幂函数形式的非线性阻尼力,进行线性化处理,并引入阻尼器方位矩阵,形成了黏滞阻尼器减震结构运动方程。

(2) 在Rosenbrock方法中,引入Sherman-Morrison定理,简化矩阵求逆的计算,形成求解局部非线性运动方程的方法。

(3) 对Rosenbrock方法求解非线性阻尼问题的稳定性进行了谱分析。结果表明,当阻尼指数大于0时,Rosenbrock方法是稳定的。

(4) 设计了一个装有黏滞阻尼器的七层平面框架模型,通过编制Matlab程序进行了地震响应分析,结果证实本文所提方法的可靠性和计算效率。

本文相关处理方法对于位移型阻尼器减震结构的地震响应分析亦有参考价值。