考虑土体基质吸力刚性挡墙基坑抗倾覆稳定性分析

师晨翔 杨永平 马际首 李镜培,*

(1.同济大学地下建筑与工程系,上海 200092; 2.上海南汇建工建设(集团)有限公司,上海 201399)

0 引 言

在大量的工程实践中,地表降雨入渗是基坑工程、边坡工程稳定性的重要影响因素,大量的工程实例和科学研究表明,入渗作用会引起土体中的吸力明显降低,进而引起土体抗剪强度的降低,同时降雨入渗会提高土体的饱和度,增加作用在基坑围护结构上的土压力,对基坑的整体稳定性产生不利影响。因此,研究地表降雨入渗以及地下水位变化对土体性质和基坑稳定性的影响,具有非常重要的理论和工程意义。

截至目前,对非饱和土,基坑整体稳定性,以及土体基质吸力的问题,国内外学者已经开展了一系列有意义的研究。非饱和土真三轴试验[1-2]的结果表明,土体强度与中间主应力大小关系密切。在基坑设计及稳定性验算中,挡墙的抗倾覆稳定性是重要的内容,基坑周边土体多为非饱和状态,但是目前抗倾覆稳定性验算还是使用基于Mohr-Coulomb(M-C)强度准则的饱和土理论[3],对土体非饱和的特性和中间主应力考虑不足。Lu 等[4-6]采用土-水特征参数α(进气值)和n(孔隙大小参数)基于有效饱和度Se建立了非饱和土体吸应力σs计算公式。李兆平和张弥[7]应用非饱和土水分运动理论,结合Fredlund非饱和土强度理论研究了降雨入渗对基坑安全性的影响。关于非饱和土基坑挡墙抗倾覆稳定性的研究,吴剑敏等[8]研究了基质吸力对基坑支护结构内力的影响;尚军[9]提出了基质吸力作用下,水泥搅拌桩抗滑移和抗倾覆稳定性的验算方法;S.A.Stanier 和A.Tarantino[10]由极限分析上限定理确定了砂性非饱和土挡墙的张拉区深度。张常光等[11-13]利用拓展类比方法建立的非饱和土平面应变抗剪强度统一解能合理考虑中间主应力的影响,具有重要的工程应用价值。

可以看出,当前对非饱和土基坑抗倾覆稳定性分析等问题的研究取得了非常重要的进展,但是对降雨入渗,地下水位变化等问题考虑还不够充分。在具体降雨强度、地下水位等的情况下,对基坑抗倾覆稳定性问题分析不够精确,对工程实践的指导意义不够,难以对基坑抗倾覆进行动态监测及分析,缺乏在降雨条件下基坑稳定性检测的理论指导。

在本文中,首先采用Gardner模型[14]定义的非饱和土水力传导系数,结合达西定律,推导得出了地下水位面以上非饱和土体基质吸力的空间分布规律。进而基于非饱和土的平面应变抗剪强度统一解,考虑非饱和土强度的中间主应力效应,提出了考虑降雨入渗条件下,基坑挡墙抗倾覆稳定系数的计算方法,并进行参数影响特性分析,为非饱和土基坑支护结构的合理设计和施工提供一定的理论基础。

1 降雨入渗条件基质吸力的分布规律

在Gardner模型[14]中,非饱和土体的水力传导系数k表示为

k=kse-α(ua-uw)

(1)

式中:ks为饱和土体的水力传导系数;(ua-uw)为基质吸力。

结合达西定律和Gardner模型,假设降雨条件下入渗强度为qs,且入渗强度恒定,可以得到地下水位线以上(Dw-y)处入渗条件下非饱和土体基质吸力的空间分布规律:

(2)

式中:α为SWCC曲线的拟合参数;α取值约为进气压的倒数;γw为水重度;Dw为地下水位线深度;y为地表以下深度;(Dw-y)表示地表深度y处与地下水位线的距离。

2 基坑挡墙抗倾覆稳定系数

张常光等[11-13]利用拓展类比方法建立的非饱和土平面应变抗剪强度统一解为

(3)

(4)

(5)

(6)

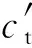
通过在式(4)-式(6)中引入统一强度理论参数,将中间主应力强度引入到土体抗剪强度的计算中。参数b取值大小的变化,反映土体抗剪强度准则的变化,b=0时不考虑中间主应力的影响,当b=1时,上述强度理论为基于双剪应力强度理论的非饱和土体抗剪强度。

将式(2)代入式(3),可以得到降雨入渗条件下非饱和土平面应变抗剪强度计算公式:

(7)

非饱和土统一总黏聚力可以表示为

ctt=

(8)

本文的计算模型如图1所示,地表降雨入渗强度均匀分布为qs,并且假设基坑挡墙为刚性挡墙,不考虑挡墙的自重、支撑、土体与基坑挡墙的摩擦,以及基坑周边超载作用的影响。图中,H表示基坑开挖深度;D表示挡墙抗倾覆嵌固深度;yot为墙后土体张拉区深度;Dw为地下水位深度,且位于挡墙墙趾以下;(σh-ua)a为作用在挡墙上的主动土压力;(σh-ua)p为作用在挡墙上的被动土压力。

图1 基坑降雨入渗条件下抗倾覆稳定性计算模型Fig.1 Calculation model of anti-overturning stability under infiltration

假设基坑周边的土体为均匀连续的非饱和土层,基于朗肯理论,可以计算作用在刚性挡墙两侧的主动土压力和被动土压力。朗肯主动土压力和被动土压力的计算方法分别为:

主动土压力强度(σh-ua)a为

(9)

式中:ka为主动土压力系数;(σv-ua)a为主动土压力区竖向应力大小,在此处(σv-ua)a=γy,其中,γ为非饱和土土体重度。

被动土压力强度(σh-ua)p为

(10)

式中:kp为被动土压力系数;(σv-ua)p为被动土压力作用区域竖向应力大小,此处(σv-ua)p=γ(y-H)。

将式(8)代入式(9),得到考虑降雨入渗条件下非饱和土主动土压力的计算公式:

(11)

在这里可以令式(11)中的主动土压力强度(σh-ua)a=0,由此得到一个关于y的一元方程,可以借助计算机辅助计算,所求得的解为基坑挡墙后张拉区深度yot。

将式(8)代入式(10),得到考虑降雨入渗条件下非饱和被动土压力的计算公式:

(12)

验算基坑挡墙的抗倾覆稳定性时,通常假定挡墙绕其墙趾转动,相应的计算公式为

(13)

式中:MSk为基坑外侧产生的侧压力对墙趾产生的倾覆力矩;MRk为基坑内侧墙被动土压力产生的抗倾覆力矩。

对主动土压力沿刚性挡墙深度进行积分可以得到墙体外侧倾覆力矩MSk:

(14)

对被动土压力沿刚性挡墙嵌入深度进行积分可以得到墙体外侧倾覆力矩MRk:

(15)

将式(14)和式(15)分别代入式(13),可以得到基坑抗倾覆稳定系数Kq的计算方法:

(16)

在Kq的计算工程中,因为在(σh-ua)aw和(σh-ua)pw的公式推导中,都引入了基质吸力的空间分布,故在本抗倾覆稳定系数的计算中,充分考虑了地表降雨入渗,地下水位的变化对基坑抗倾覆稳定性的影响。

3 算例计算与参数影响特性分析

3.1 基坑抗倾覆参数影响分析

本算例假设在黏土地区的基坑中,开挖深度H为8 m,基坑挡墙嵌固深度D为10 m,起始地下水位深度Dw为18 m,有效黏聚力c′为3 kPa,有效内摩擦角φ′=20°,统一强度理论参数b=1,均质非饱和土体重度γ=19 kN/m3,α为SWCC曲线的拟合参数,α=0.005 kPa-1,地表入渗速率qs=0 m/s,饱和土体的水力传导系数ks=5×10-8m/s,水体重度γw=10 kN/m3,吸力角φb=12°。

图2给出了统一强度理论参数b分别为0～1时的基坑,分阶段降水,基坑抗倾覆稳定系数Kq随降水深度增加的变化规律。由图8可以看出,b的不同取值,反映了中间主应力的考虑程度,对于b不同取值条件下,地下水位的下降会不同程度地提高抗倾覆稳定性。同时,伴随着b取值增大,基坑抗倾覆稳定性明显增加,这也充分说明,中间主应力在基坑抗倾覆稳定性的巨大影响。

图2 基坑抗倾覆稳定性随地下水位的变化Fig.2 Variation of anti-overturning stability of the foundation pit under different de watering depths

图3为基坑抗倾覆稳定系数Kq伴随着统一强度理论参数b之间的关系,同时反映不同有效内摩擦角对基坑抗倾覆稳定性的影响。由图可知,土体内摩擦角的变化对基坑抗倾覆稳定性有明显影响,基坑抗倾覆稳定性随内摩擦角的增大而增大。

图3 中间主应力对基坑抗倾覆稳定性的影响Fig.3 Effect of intermediate principal stress on anti-overturning stability of the foundation pit

图4展现了基坑挡墙在不同嵌固深度下,基坑抗倾覆稳定性与统一强度理论参数b之间的关系。从图中可知,基坑嵌固深度的增加有利于增加基坑抗倾覆稳定性,中间主应力对基坑抗倾覆稳定性有益。

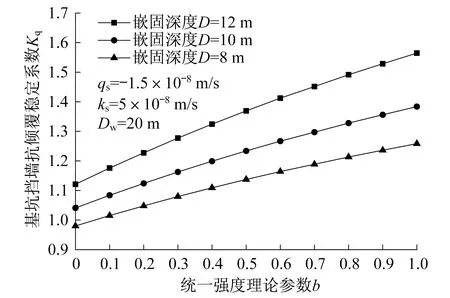
图4 嵌固深度对基坑抗倾覆稳定性的影响Fig.4 Effect of embedment depth on anti-overturning stability of the foundation pit

3.2 降雨入渗条件影响分析

图5反映了不同入渗条件下,本文计算方法基质吸水位面以上的空间分布规律。从图中可以看出,在没有降雨入渗条件下,基质吸力随距离地下水位线高度的增加展现出线性单调增大的趋势,对应图1中基坑抗倾覆计算模型,地下水位线以上土体,竖向距离越远,土体中基质吸力越大。降雨入渗条件下,基质吸力的大小明显降低,并且入渗强度越大,基质吸力强度幅度越大,同时基质吸力距离地下水位线高度的增加,其增幅有逐渐放缓的趋势。

图5 地下水位线以上土体基质吸力空间分布规律Fig.5 Distribution of soil matric suction above the ground water table in soil

图6中给出了,不同降雨入渗条件下,基坑地下水位不同位置情况下,基坑挡墙的抗倾覆稳定系数Kq的变化规律。从图中可以看出,降雨入渗对基坑抗倾覆稳定性有明显影响,伴随着降雨入渗强度的增强,基坑抗倾覆稳定性降低。同时,降雨入渗强度增大时,基坑伴随地下水位降低抗倾覆稳定系数增长的幅度较小。

图6 降雨入渗对基坑抗倾覆稳定性的影响Fig.6 Effect of the infiltration on anti-overturning stability of the foundation pit

3.3 不同基质吸力分布形式对比

为了进一步研究本文降雨入渗条件对基坑抗倾覆稳定性的影响,在此与工程中常用基质吸力计算方法相比较。基质吸力是非饱和土与饱和土的一个重要区别,与降雨,蒸发等因素关系密切,目前在工程应用中,主要采用近似假定基质吸力均匀分布,或者沿深度线性减少到地下水位Dw处这两种方式,如图7所示。

图7 基质吸力分布Fig.7 Distribution of soil matric suction

图8分别给出了本文基质吸力算法与基质吸力均匀分布和基质吸力沿深度线性分布条件下,基坑挡墙抗倾覆稳定系数Kq与统一强度理论参数b的关系图。从图中可以看出,随着地表基质吸力的增加,基坑抗倾覆安全系数Kq不断增加。从中可以看出,基坑挡墙抗倾覆计算中,忽略基质吸力对非饱和土强度的影响,计算将偏保守。同时,有图8(a)和图8(b)对比可以看出,相同地表强度下,按照基质吸力沿深度减小到地下水位为0的算法,基坑抗倾覆稳定性计算更加保守。相比与均匀分布和线性递减的基质吸力分布,本文方法可以根据入渗强度,土体性质,计算基质吸力的具体分布,计算更加精确。

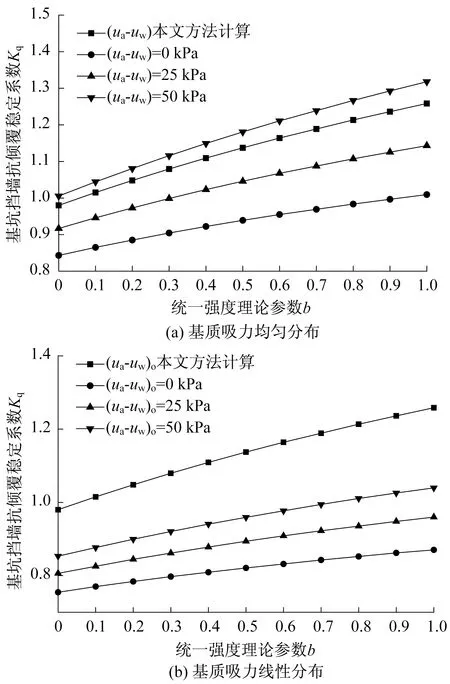
图8 基质吸力分布方式对基坑抗倾覆稳定性的影响Fig.8 Effect of the distribution of soil matric suction on anti-overturning stability of the foundation pit

4 结 论

本文基于非饱和土的平面应变抗剪强度统一解,推导了降雨入渗条件下基坑抗倾覆稳定性计算公式。分析了降雨入渗强度,嵌固深度,土体内摩擦角,统一强度理论参数等因素对基坑抗倾覆稳定性的影响,通过算例分析和方法对比,可以得出以下结论:

(1) 中间主应力σ2对基坑抗倾覆稳定性验算有较大影响。通过参数b的引入,考虑中间主应力σ2效应,在基坑抗倾覆计算中可以更好地考虑非饱和土的强度潜能,更客观地反映基坑抗倾覆稳定性。

(2) 基坑抗倾覆稳定性与地下水位深度密切相关。基坑降水对土体强度有直接影响,伴随着基坑降水深度的增加,土体基质吸力的作用增强,提高了土体的强度,同时减少土体重度,提高基坑抗倾覆稳定性。

(3) 降雨入渗对基坑抗倾覆存在重大影响。降雨入渗强度的增加,会明显改变基质吸力的分布,并且降低基质吸力的大小,进而对土体强度产生不利影响,降低基坑抗倾覆稳定性。

(4) 土体内摩擦角对基坑抗倾覆稳定性存在较大影响。土体内摩擦角增大,土体基质吸力产生的粘聚力提高,进而增大了抗剪强度,对基坑抗倾覆稳定性有益。

(5) 基坑挡墙嵌固深度与基坑抗倾覆稳定性关系密切,增加挡墙嵌固深度有利于基坑抗倾覆稳定性的提高。