基于Abaqus蠕变本构的重载路面车辙分析
2018-07-14宋海云
宋海云
(天津市交通科学研究院,天津 300074)
0 引 言
当前,我国高等级公路上重载、超载问题十分突出,因此极大地缩短了沥青路面的使用年限。大量理论研究和试验观测表明,重载条件下沥青路面主要损坏类型表现为行车道轮迹带车辙与裂缝。沥青混合料在荷载作用下产生较大的塑性变形,由于渠化交通的作用,荷载及荷载重复次数的增加,导致塑性变形的累积[1]。在炎热地区,很多沥青路面都出现了泛油、车辙等高温稳定性不够的问题,严重影响沥青路面平整度与行车安全。车辙是渠化交通下高等级公路沥青混凝土路面的主要破坏形式之一。车辙发展到一定程度会使得车辆变道时方向失控。雨天会产生车辙内积水,引发路面的水损害以及车辆的漂滑。研究成果表明,我国高速公路养护费用中有90%用在了车辙上。因此研究车辙的产生机理可以指导沥青混凝土路面的结构设计。在正常情况下,沥青路面的车辙包括结构型车辙、流动型车辙及磨损型车辙三种类型。沥青路面的永久性变形基本上都属于沥青混合料的流动变形[2]。在我国,由于基层多采用半刚性材料,强度较大,结构型车辙很少。因此,车辙主要为第二类流动型车辙。半刚性基层沥青路面耐久性差,使用寿命短的情况,己成为阻碍中国道路建设发展的主要问题。同时有研究表明,在移动荷载作用下,较低的车速会使路面结构产生较大的应力,不同车速下路面结构的最大垂直压应力、最大水平压应力、最大剪应力随车速的减小而相应增大,并且基本呈现线性变化,所以车速也是影响路面车辙的重要因素[3-4]。
1 时间硬化蠕变模型理论
路面变形可以分为弹性变形和非弹性变形两部分。在加载瞬间产生瞬时弹性变形,以后的变形为由粘性变形和塑性变形耦合的蠕变变形。蠕变主要是利用实验配合数值方法获得材料参数后,再将所获的参数使用于有限元的分析中,以求获得其应力、应变、蠕应力、蠕应变等内部结构经外力、时间或温度所造成的效应[5]。Abaqus软件蠕变分析模式,通常采用三种蠕变定律描述粘塑(visco-plastic)材料行为。幂次法则模式(Power-law model)可应用于仿真等温与固定负载下之蠕变行为,其所采用之定律分别为时间硬化率(time hardening)及应变硬化率(strain hardening)关系式。其中,时间硬化模型适用于分析过程中应力状态恒定不变的情况,而应变硬化模型适用于分析过程中应力状态发生变化的情况。由于实际路面车辙的发生总是伴随着应力状态的变化(如轴重的变化),故一般采用Abaqus中应变硬化蠕变模型进行车辙计算分析。路面材料的单轴等效蠕变应变率εcr为温度T、应力q和时间t的函数[6],可用式(1)表示:
εcr=f(T,q,t)
(1)
若在分析过程中所受应力q保持不变时,Abaqus中采用的时间硬化蠕变模型的表达式为
εcr=Aqntm
(2)
式中:εcr为单轴等效蠕变应变率;q和t分别为应力和时间;A,n,m为模型参数,一般通过室内材料蠕变试验确定A>0,n>0,-1 若在分析过程中所受应力q变化时,Abaqus中采用的应变硬化蠕变模型的表达式为 (3) 参数含义同前。 选择典型的半刚性基层沥青路面结构进行分析。以半刚性基层沥青路面为建模参考物,采用如图1所示典型的半刚性路面结构。 图1 典型半刚性基层路面结构Fig.1 Typical semi-rigid base pavement structure 利用商用有限元计算软件Abaqus建立路面结构二维实体模型,模型宽度取一个车道宽度3.75 m,路基深度方向取3 m。该模型满足以下基本假设:将沥青面层材料视作非线性黏弹性体。基层以下部位均为弹性材料,路面各层完全连续,具有各向均匀及各向同性的性质,属于小变形工程问题,各结构层层间完全连续,不计路面结构体自重。 采用二维平面应变模型对车辙产生过程中沥青面层蠕变应变的发展规律以及车辙产生后路面变形状态进行研究。选择“四边形、八节点”单元CPE8R,“四边形、八结点” 等参单元是较高精度的二维有限元单元,由于路面结构是形状规则的矩形体,采用矩形单元就可以满足路面结构边界上的形状条件。将双圆荷载简化为双矩形荷载。 路面结构加载示意图及网格化分示意图,见图2、图3。 图2 路面结构加载示意图Fig.2 Schematic diagram of pavement structure loading 图3 路面结构网格划分示意图Fig.3 Schematic diagram of pavement structure meshing 计算线弹性层状体系下不同轴载的路面弯沉。一般考虑了轴载增加时的两种轮胎情况:第一种为轮胎接地压强随轴载增加,第二种为轮胎接地压强增加而轮胎作用半径不变。两种情况下,计算弯沉在应用范围内几乎相等[7]。为了简化模型使用第二种方法只改变轮胎的压强而不改变轮胎的接地半径。 车辙一般是在温度较高的季节,沥青路面在车辆反复碾压下,产生塑性流动而逐渐形成的。路面结构中沥青混合料蠕变参数分析时,应选取60 ℃的高温条件下对应的参数值。材料弹性参数和蠕变参数取值如表1所示[8]。 汽车荷载的频繁加载和卸载是产生路面结构车辙的原因,将路面结构所承受的多次荷载等效为汽车荷载长时间作用,则可以模拟汽车荷载多次作用在路面结构上。这样在定义Abaqus分析步的时长时,就可以将荷载作用次数转化为荷载的累计作用时间。 表1沥青混合料参数表 Table 1 Parameters of asphalt mixtures 表2其他材料参数表 Table 2 Parameters of other materials 计算公式如下: (1) 式中:t为轮载累计作用时间,s;N为轮载作用次数;P为车辆轴重,kN;nw为轴的轮数,个;p轮胎接地压力,MPa;B为轮胎接地宽度,cm;v为行车速度,km/h。 如加载时间取100 604 s,相当于标准轴载100 kN,以车速60 km/h,对路面产生累计标准轴次1 000万次的累计作用时间。本文分别采用轴重为100 kN、130 kN、150 kN、180 kN和200 kN,按照静力等效原则,分别对应轮胎压强0.7 MPa、0.91 MPa、1.05 MPa、1.26 MPa和1.4 MPa,采用五种工况模拟车辆荷载作用1 000万次的过程。标准轴载作用下路面永久变形云图,见图4-图6。 由图4可知,半刚性基层路面结构在60 ℃的高温和重载反复作用下,沥青混凝土层随着荷载次数的增加发生了缓慢的变形,变形量的大小和路面的不同位置的应力大小有关。轮载作用的位置塑性变形明显,有较大的下陷。同时两轮中心的沥青混凝土承受了一定的挤压,轮载外侧同样承受了一定的挤压。 图4 路面永久变形云图(作用200万次)Fig.4 Contour plot of permanent deformation in pavement (2 million loading times) 图5 路面永久变形云图(作用1 000万次)Fig.5 Contour plot of permanent deformation in pavement (10 million loading times) 图6 不同荷载作用下路面永久变形图Fig.6 Permanent deformation of pavement under different loads 由图5和图6可知,半刚性基层路面结构的塑性变形都随着荷载作用次数的增加而增加。同时变形的增加速度都是前期增长较快,后期增长较慢,并逐渐趋于稳定。轴重的增加对路面永久变形有明显的影响。荷载作用10 000 s时(作用次数115.7万次),在轴重由100 kN增加到200 kN的过程中,路面永久变形由30 mm增加到了62 mm。当作用时间达到100 604 s (作用次数1 000万次)时,在轴重100 kN增加到200 kN的过程中,路面永久变形从102 mm增加到了117 mm。整个过程表明,重载对路面车辙变形的影响前期比后期更明显,且轴重越大车辙变形越大。 考虑到影响重载的移动速度也会影响到路面结构车辙的深度,在轴重为200 kN温度为60 ℃的情况下,选取行驶速度分别为40 km/h、60 km/h、80 km/h、100 km/h和120 km/h五个行驶速度,分别作用在路面结构上1 000万次,对应的作用时间分别为50 300 s、60 300 s、75 400 s、100 604 s以及150 900 s。由于每个工况对应的行车速度不同,则对应的作用时间不一致。每个工况对应的行车速度与路面永久变形的关系,见图7-图11。 图7 120 km/h作用1 000万次变形图Fig.7 Deformation of 10 million loading times at 120 km/h 图8 100 km/h作用1 000万次变形图Fig.8 Deformation of 10 million loading times at 100 km/h 图9 80 km/h作用1 000万次变形图Fig.9 Deformation of 10 million loading times at 80 km/h 图10 60 km/h作用1000万次变形图Fig.10 Deformation of 10 million loading times at 60 km/h 图11 40 km/h作用1 000万次变形图Fig.11 Deformation of 10 million loading times at 40 km/h 由图7-图11可知,在不同速度作用1 000万次后路面永久变形量为128 mm、117 mm、110 mm、105 mm、和101 mm。当行车速度由40 km/h提高到60 km/h时,路面永久变形降低了8.59%;当行车速度由60 km/h提高到80 km/h时,路面永久变形降低了5.98%;当行车速度由80 km/h提高到100 km/h,并最后提高到120 km/h时,路面永久变形分别降低了4.54%和3.81%。 这说明,在其他因素不变的情况下,行驶速度可以影响路面的永久变形,且车速越慢变形越大。在同样的交通量下,提高车速能够有效地减小路面的永久变形。 随着行驶速度的增加,路面车辙的发展规律仍然是前期发展较快,后期逐渐趋于稳定。速度对于路面的永久变形的影响并没有轴重的影响大,但也是不容忽视的问题。 (1) 随着荷载次数的增加,路面会发生缓慢的变形,且变形程度随着荷载作用次数的增加而增加。轮载作用的位置塑性变形明显,有较大的下陷,轮载外侧同样承受了一定的挤压。重载交通对路面的永久变形影响明显,变形随轴重的增加而增加。在开放交通初期,重载会对沥青混凝土造成严重的车辙破坏,应适当限制重载车辆的运行。 (2) 在其他条件一致时,针对同一种轴载,速度越快路面永久变形越小。重载作用下,路面变形值往往要大于标准轴载的作用,尤其是在速度较低的情况下,这种差别会更大。这说明,行车速度越大对路面车辙的影响越小,所以在保证安全的前提下,针对高等级公路可以适当地提高最低行车速度。 (3) 速度对于车辙的影响小于重载对于路面车辙的影响,但不容忽视。因为在实际交通中,超载车辆往往不会具有较高的行驶速度,因此应积极限制慢速条件下的超载车辆。2 路面结构选取及参数确定
2.1 路面结构的选取及模型建立



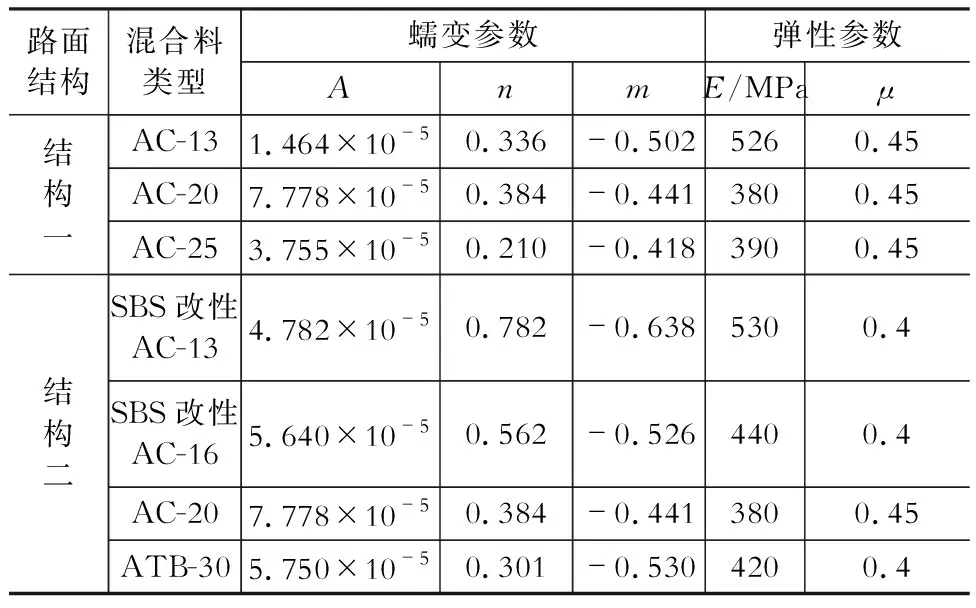
2.2 路面结构层参数选取
3 重载交通条件下路面车辙分析
3.1 不同轴载作用下的车辙分析



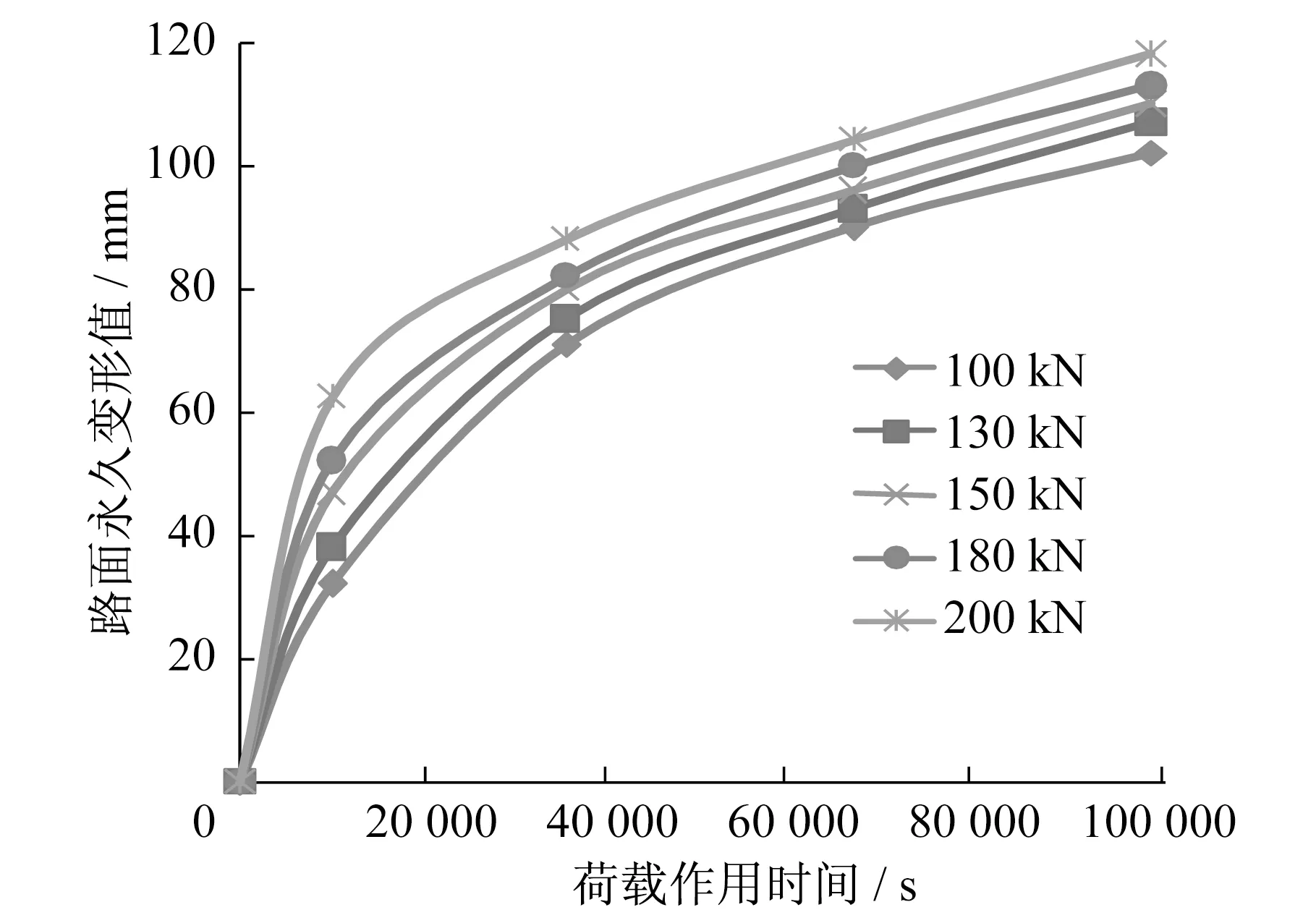
3.2 不同速度重载作用下的车辙分析


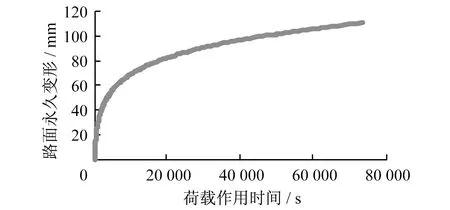
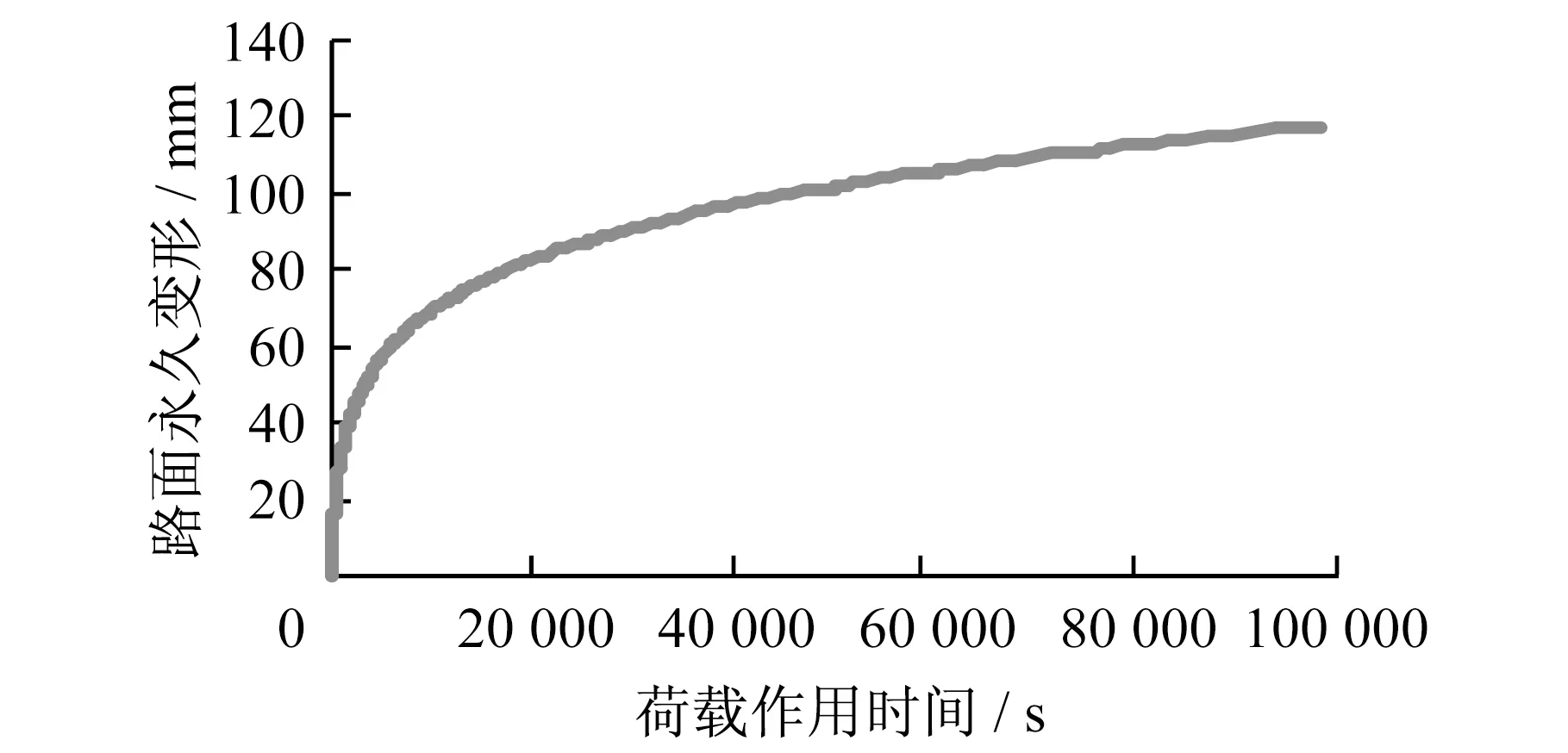

4 结 论
