串列螺旋桨空化特性数值分析

杜晓旭, 张正栋

(西北工业大学 航海学院, 陕西 西安　710072)

随着船舶主机功率的以及螺旋桨负载的增大，螺旋桨空化、噪声问题更加突出，一种新型的螺旋桨——串列螺旋桨进入人们的视野。串列螺旋桨是一种2个普通螺旋桨位于同一转轴且转速及旋转方向相同的特种推进器。与其他特种螺旋桨相比，它构造简单，加工、安装及维修更加方便，且当负载较大时，推进效率有所提高[1]。串列螺旋桨在一段时期并没有得到发展，在20世纪60年代以后，串列螺旋桨才再次引起人们的兴趣，国内外学者也做了一定的研究[1]。但总体来说，有关串列螺旋桨方面的研究较少，有关串列螺旋桨空化的研究更是少之又少，因此本文研究将对串列螺旋桨的发展奠定一定的基础。

对于螺旋桨空化特性的研究，主要有实验和数值模拟2种方法，前者耗时耗力且需要一定的实验条件，而随着计算机技术的发展，计算流体力学(CFD)技术蓬勃发展，基于数值模拟技术进行科学研究已经成为现在的研究主流，而且其具有信息量全且容易实现的特点，深受研究者们的喜爱。基于势流理论及黏流理论，利用面元法及求解RANS方程来数值模拟螺旋桨水动力特性及空化特性的技术已经日渐成熟，且通过研究者们进行对比，数值计算结果相当可靠，目前国内外已经取得了很多相关成果[4]。对于串列螺旋桨水动力特性，余欣[7]基于CFD方法对串列螺旋桨的水动力性能展开较为系统的研究；王超等人[8]通过求解RANS方程对串列螺旋桨水动力性能展开数值预报，并与试验结果进行对比，发现该方法计算结果与试验结果吻合。

对于串列螺旋桨空化方面的研究，目前并没有相关的论文，考虑到Ahn等人[9]基于非结构化网格，通过求解多相流RANS方程计算了P4381型螺旋桨的定常流空化特性，发现数值计算结果能够很好地预报空化的尺寸及形状等，认为通过数值模拟方法分析串列螺旋桨空化特性是可行的。故本文基于黏性流理论及多相流理论，结合剪切应力SST k-ω湍流模型及Z-G-B (Zwart-Gerber-Belamri)空化模型，通过求解RANS方程来求解三维全通道串列螺旋桨的定常空化流场，通过研究不同进速系数及不同空化数下串列螺旋桨的性能，为串列螺旋桨的设计和研究提供一定的参考。

1　数值方法

1.1　控制方程

在数值分析螺旋桨空化特性时需考虑汽液两相混合流模型，该模型考虑了流场在相变过程中两相间的相互影响以及滑移速度，通过相变率引入空化模型。当发生空化时，空化流体通常表示为水及水蒸汽的混合物，因此空化流场表示为密度可变的统一混合流场。在这里引入汽相传输方程来求解汽相体积分数，可以得到混合密度ρm与空泡相质量分数fv的关系如下:

(1)

因此混合流的控制方程[10]在直角坐标系下的张量形式如下:

式中,i,j=1, 2, 3;ρv为空泡相密度;ρl为液体相密度;ui,uj为混合相速度;xi,xj为空间坐标分量;μm为混合黏性系数。

1.2　空化模型

相较于应用最广泛的Singhal空化模型,Z-G-B空化模型[11]能够更好地模拟发生空化时空泡从出现到增大的过程,且在传质速率相中考虑了非凝结气体(NCG)体积分数的影响,因此本文选用Z-G-B空化模型。其控制空泡体积分数φv的方程定义为:

(4)

(5)

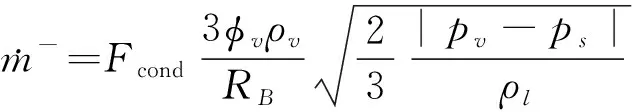
(6)

式中,Fvap和Fcond分别是空泡衍生和凝结的经验系数;RB是空泡半径;φNCG为NCG体积分数;pv为空泡内压强;ps为空泡周围压强。

SST k-ω湍流模型[12]能够更加精确地预报存在负压时流体的分离量以及更好地处理不同边界层问题,在计算复杂螺旋桨流场时有更广泛的适用性,故本文选用SST k-ω湍流模型来封闭RANS方程。

2　计算模型与网格划分

2.1　几何模型

本文以标准CLB4-55-1串列螺旋桨[13]为仿真模型,其主要参数如表1所示。

表1　CLB4-55-1串列螺旋桨几何参数

桨模叶剖面和叶轮廓与荷兰Wageninger水池的B系列相同,有关型值点见文献[13],但螺距径向不变,且无后倾角。

与普通螺旋桨相似,模型建立于直角坐标系。Y轴为旋转轴,指向来流方向;X轴为桨叶的叶面母线方向,由叶根指向叶梢;Z轴负荷右手螺旋定则。通过坐标转换,将二维型值点文件通过MATLAB程序转化到所建三维坐标系,对叶梢与叶根做适当处理。为了更好地模拟来流,在桨毂前后端添加半球体导流帽与尾流罩。同时,为了提高数值计算的精度,采用全通道模型展开数值计算,几何模型如图1所示,红色桨叶为后桨。

图1　串列螺旋桨几何模型

2.2　网格划分

网格划分直接影响数值计算精度与速度,划分高质量的网格是数值计算必须满足的条件。鉴于本文所计算的旋转模型,采用分块混合网格的方法划分高质量网格。将计算域分为静止域与旋转域两部分,旋转域包含螺旋桨,为旋转计算域。2个域通过交界面来传输数据。由于交界面之间存在滑移,故通过滑移网格技术来模拟2个域之间的相互作用。

计算域为半径5D,长10D的圆柱体,入口距螺旋桨4D。静止域采用六面体结构化网格,旋转域采用非结构化四面体网格,采用分区域加密的手段在螺旋桨周围加密网格,在螺旋桨叶面划分5层三棱柱边界层网格,第一层网格高度约为0.000 1D,总体网格数约为280万。计算域及网格如图2、图3所示所示。

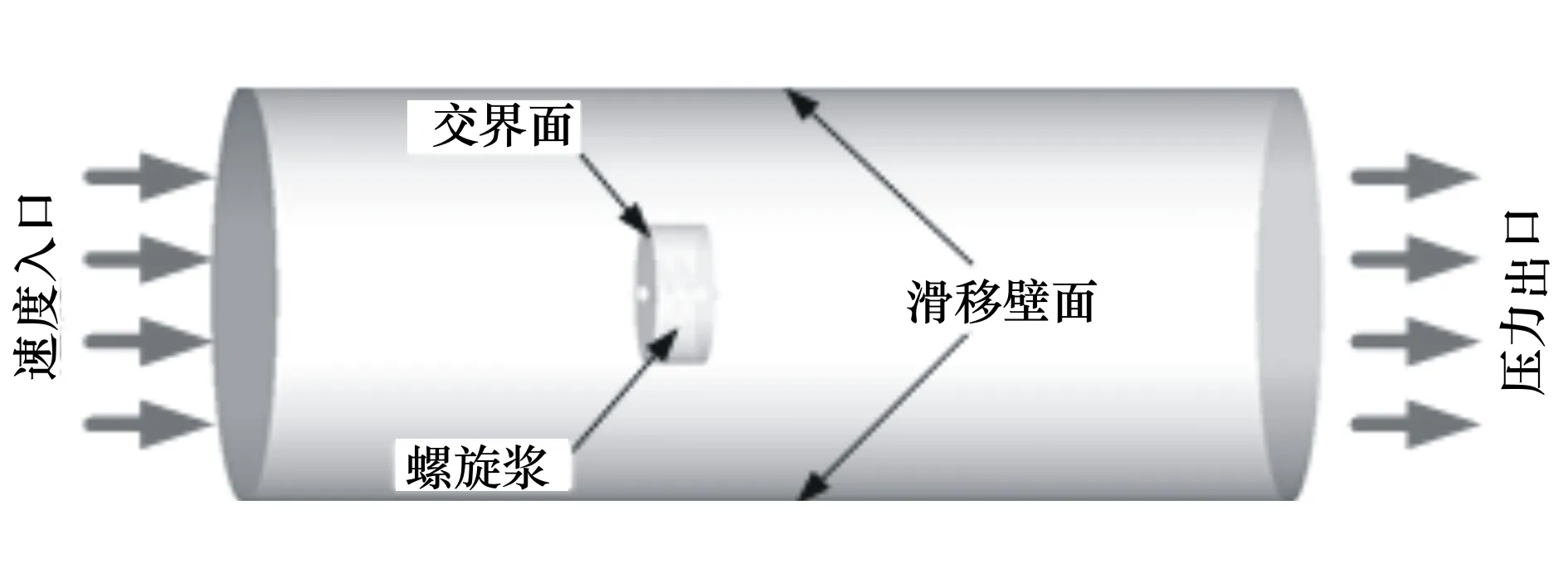
图2　计算域及边界条件

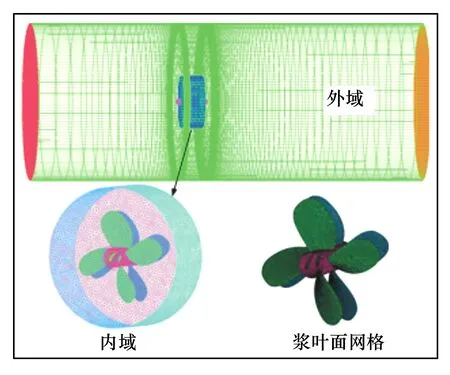
图3　网格划分

2.3　计算方法与边界条件

本文采用有限体积法(FVM)来离散RANS方程,采用高精度差分格式进行空间离散,采用Euler后插格式进行时间离散。入口边界为速度入口,湍流强度为5%,液体的体积分数为1,空泡的体积分数为0,液体温度25°,饱和蒸汽压为3 540 Pa,空泡的平均直径为2 μm,出口边界为压力出口,由空化数σ=(pout-pv)/0.5ρlV2进行控制,V为来流速度,螺旋桨壁面为无滑移壁面,近壁区域采用增强壁面函数模型,在圆柱壁面采用自由滑移壁面条件。本文通过结合全隐式耦合及并行计算技术来提高技术速度与稳定性,收敛条件为10×10-5。

3　数值计算

为了方便对计算结果的处理与分析对比,特对相关物理参数进行无量纲化处理:进速系数J=V/nD,串列桨推力系数为KT=(T1+T2)/ρn2D4,扭矩系数KQ=(Q1+Q2)/ρn2D4,敞水效率为η=KT/KQ*(J/2π)。其中:n为螺旋桨转速,在本文取900 r/min,T1与T2分别为前后桨推力,Q1与Q2分别为前后桨扭矩。

3.1　水动力特性及空化特性验证

为了验证本文所建立几何模型及定常非空化流场数学模型的精确性,本文首先对数值计算的网格无关性进行验证,通过调节网格尺度来改变网格数目,表2所示为不同网格数目下CLB4-55-1串列螺旋桨推力系数,可以看出当网格数目达到280万时,计算结果已经几乎保持不变,故选择280万网格作为全文计算网格。基于网格无关性测试,对进速系数J从0.4～1.1变化的CLB4-55-1串列螺旋桨水动力系数进行计算,并与实验值进行对比,对比结果如图4所示。

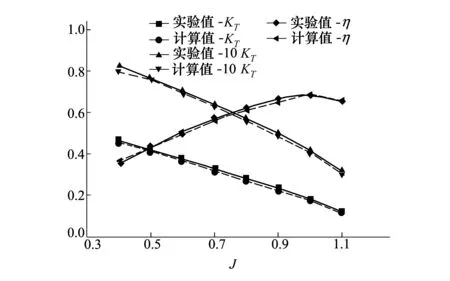
图4　水动力特性对比曲线

可以看出,推力系数KT与10倍扭矩系数10KQ与实验值基本吻合,当进速系数为0.4时,KT与实验值的误差最大,为0.023,误差约为2.87%,故本文所建立非空化计算模型计算结果是可靠的。

为了验证本文所建立空化模型的准确性,特选取二维NACA66翼型作为算例进行空化验证。利用ANSYS FLUENT软件展开定常空化性能数值计算。计算网格及边界条件设置如图5所示。

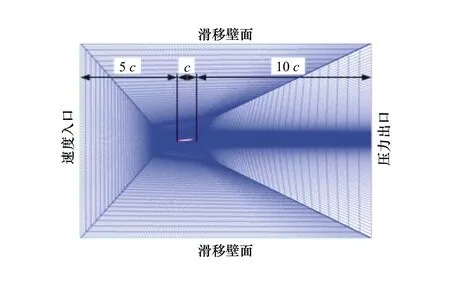
图5　NACA66翼型网格划分及边界条件设置

翼型弦长c为100 mm,翼型攻角α=2°,翼型表面为无滑移壁面。计算设置时,选用液态水及水蒸汽,密度分别为998.2 kg/m3及0.001 9 kg/m3,温度为25°C,饱和蒸汽压为3 540 Pa,来流速度设为10 m/s,通过改变出口压来调节空化数σ。

表2　网格无关性测试

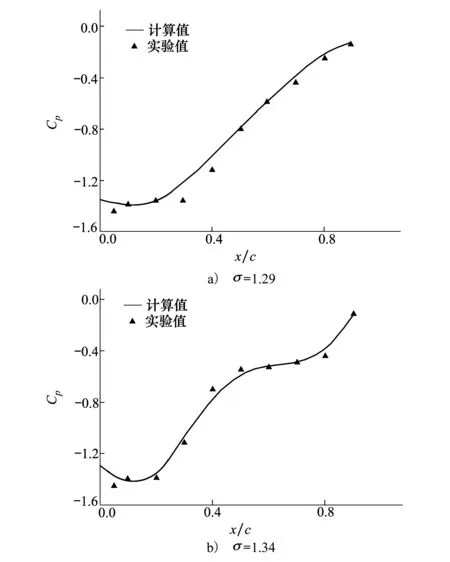
图6　数值计算结果与实验结果对比

图6为2种最为经典的空化数σ对应的翼下表面的压力系数弦向分布图,压力系数Cp=(p-pout)/1/2ρlV2,图中x为压力点位置与导边的距离。由图可知,本文数值计算结果除了导边处其他地方与实验值[10]基本一致,通过上述算例计算结果对比实验验证了本文空化模型的精确性及所选择数值计算方法的可靠性,从而保证了后续计算结果的可靠性。

3.2　不同进速系数时计算结果分析

为了研究不同进速系数对串列螺旋桨空化特性的影响,本文通过调节来流速度来改变进速系数,本文进速系数变化范围为0.6～1.2。

图7　不同空化数敞水推力特性曲线

图7所示为不同空化数对应的串列螺旋桨敞水推力特性曲线与敞水非空化推力特性曲线对比图,可以看出,空化数越小,进速系数越小,空化现象越明显,导致螺旋桨推力越小。当σ=1时,在所有进速系数范围内,螺旋桨均发生空化,故推力系数整体低于非空化推力系数,随着进速系数增大,推力系数先增加后减小;当σ=2时,进速系数小于0.7时,空化面积很大,推力系数与σ=1时的推力系数相差不大。当进速系数大于0.7小于1时,桨叶局部空化,推力系数有所增加,当进速系数大于1时,桨叶不发生空化,推力系数与非空化推力系数非常接近;当σ=3时,低进速系数时,桨叶出现局部非空化,因此推力系数相比于低空化数时有所增加;当σ=4时,由于空化数较大,因此发生空化面积较小,故当进速系数大于0.9时,已不再产生空化现象,推力系数也无变化。当σ=4.5时,已经不再发生空化,敞水推力特性与非空化推力特性十分接近。总之,空化数越大,出口压力越大,液态水的汽化压力与当地流体压力的差值越来越大,因此空化现象逐渐消失。

图8为2个不同空化数σ=2及σ=3时桨叶的吸力面空化云图。空化数σ=2时,可以清楚地看出随着进速系数的增大,空化区域减小。当进速系数为0.6时,前桨吸力面已经完全空化,后梁除了靠近桨毂的区域外,其他地方也完全空化,该进速系数空化现象明显。当进速系数为0.8时,前桨与后桨都为局部空化,这也与图7敞水推力系数变化曲线向对应。需要提到的是,当进速系数为0.9时,后桨空化区域比前桨空化区域更大,可能有2个原因：①后桨螺距较前桨大0.1,空化性能差于前桨;②前桨尾流场对后桨由影响,在后桨空化区域出现回流涡,流体速度增大,压强减小,发生空化。当进速系数大于0.9时,已经不再发生空化。空化数σ=3时,空化现象明显有所抑制,当进速系数为0.6时,前桨和后桨都为局部空化。当进速系数为0.8时,前桨已经不发生空化,而后桨在叶梢附近还有局部空化。当进速系数大于0.8时,不发生空化。对比同一个进速系数不同空化数的桨叶空化图可发现,空化数越小,空化区域越大,空化现象越明显。

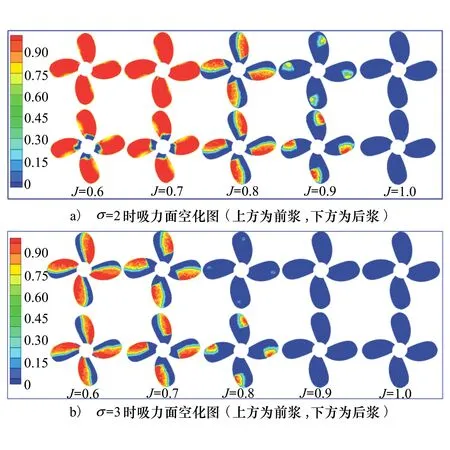
图8　不同进速系数时吸力面空化云图

3.3　不同空化数时计算结果分析

图9所示为空化数在1～4.5变化的串列螺旋桨敞水效率曲线,由图可以看出,对于固定的进速系数,随着空化数的增加,效率呈现先增加后基本不变的趋势,分析其原因,当空化数小时,空化现象尤为明显,前桨及后桨的吸力面几乎都被气体覆盖,导致效率有很大的损失,而随着空化数增加,空化现象消失,因此效率逐渐保持不变。进速系数越大,效率损失越少,进速系数是有由来流速度决定的,来流速度越大,对于固定空化数,出口压力也越大,同时桨叶部分的动压越大,因此液态水的汽化压力与叶片部分流体压力的差值越大,空化现象被抑制,甚至当进速系数为1.1时,基本不发生空化。当进速系数为0.7时,效率损失尤为验证,近乎20%,由图7可知,此时推力损失较大,故导致效率损失较大。

图10为进速系数为0.9时不同空化数时的桨叶空化云图,可以看出随着空化数的增加,空化现象得到抑制,最后消失。当空化数σ=1时,前桨除了叶根靠近桨毂处没有空化,其他部位都发生空化,而后桨有几乎1/3的叶面积为发生空化,区域为靠近桨毂处,这是由于靠近桨毂处的流体速度较低造成的。而当空化数σ=1.5时,空化区域随着流体运动方向向桨叶随边处移动,前后桨发生空化区域几乎一致,而当空化数σ=2时,前桨空化区域几乎消失,只剩一小部分区域发生空化,而后桨由于前桨尾流场的加速作用,还有较大区域发生空化。当空化数σ>2时,空化现象消失,可见对于进速系数为0.9,该型串列螺旋桨不再发生空化。

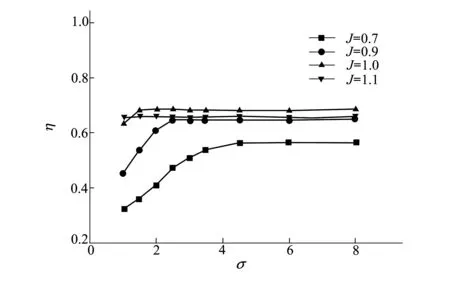
图9　不同空化数时敞水效率

图10　不同空化数吸力面空化云图(上为前桨，下为后桨)

4　结　论

本文基于混合网格的RANS方法来分析和预报了CLB4-55-1型串列螺旋桨在均匀来流情况下的空化性能，在完成该桨水动力特性及经典空化算例验证的基础上，对不同进速系数及不同空化数下的串列螺旋桨空化性能展开数值预报，通过分析得到以下结论：

1)对CLB4-55-1螺旋桨进行非空化敞水定常水动力计算，计算结果与实验结果一致，验证了本文所建立几何模型及网格划分的准确性与可靠性；对NACA66翼型进行定常空化性能数值模拟，对于不同空化数下的翼型压力分布于实验结果基本一致，验证了所建立空化模型的合理性与实用性。

2)随着进速系数的升高，螺旋桨空化情况下敞水推力系数呈降低趋势；空化数越大，空化推力系数与非空化推力系数之间的差越小；进速系数越小，空化现象越明显；当进速系数为1时，非空化推进效率最大，当进速系数大于1时且空化数大于1时，几乎不发生空化，对空化效率无较大影响。

3)随着空化数的增大，空化现象逐渐被抑制，最后空化消失；发生空化时，敞水推进效率有明显下降，进速系数越小，空化越明显，效率下降越多；随着空化消失，推进效率逐渐基本不变；当进速系数为0.9时，空化数小于2时，空化现象明显，大于2时不发生空化。

4)串列桨空化特性与单桨基本一致，在低进速系数及低空化数时，前后桨吸力面均发生大面积空化，但当进速系数增大到0.8时，空化现象逐渐被抑制，此时由于前桨对流场的加速及回流涡的存在，后桨空化面积略大于前桨空化面积，当空化数达到某一值时，前后桨空化现象消失。