基于复杂系统退化机理的备件订购策略模型

王成, 许建新, 王红军, 张振明

1.西北工业大学 机电学院, 陕西 西安　710072;2.北京信息科技大学 现代测控技术教育部重点实验室, 北京　100192

随着装备的结构越来越复杂，精度越来越高，对装备的安全运行提出了更高的要求。装备运行状态的实时有效感知和状态判断对其安全运行至关重要，特别是对于一些高端装备复杂系统模块的退化状态预测和备用系统的有效订购是保障安全有效运行、提升服务质量、降低维修成本的关键。高端装备的诸多系统往往属于复杂系统，具有集成度高、退化状态预测难和维修困难等特点，同时其订购的备用系统具有价格昂贵、稀有和较长交付时间等特点，为了降低总体维修成本，大多数企业一般都采用预防性替换(preventive replacement,PR)的维修策略。在PR策略中，主要分为2类，基于时间的维修(time-based maintenance,TBM)策略和视情维修(condition-based maintenance,CBM)策略。对于前者，主要关注系统的寿命分布模型。对于后者，主要依据系统退化水平或健康状态作为决策依据。与前者相比，后者是一个更有前景的维修策略，因为它强调将数据驱动与状态监控数据相结合，而且往往针对具体的维修对象。因此，后者在学术界和工业界都受到相当广泛关注[1-3]。特别是最近几年，基于计算机的状态监测技术(computer-based condition monitoring,CBCM)(如先进的传感器技术)和物联网(internet of things,IoT)的快速发展进一步促进了视情维修的实践和发展。

大多数CBM策略都是在这样的假设下研究的，即在任何时刻都有无限量供应的可用于替换的备件。然而，当可用备件有限和/或交付时间比较长时，这种假设通常是不现实和不切实际的。当备件价格昂贵，稀缺且随机交付时间越长，考虑缺货成本和库存成本就显得尤为重要。那么，在工程实践中何时进行备件订购才能使整个维修成本最小是一个非常重要的问题。受这类问题的驱使，一些订购策略已被广泛研究。

Chien等[4]提出了一个基于年龄的备件订购策略，该策略同时考虑了常规交付时间和紧急交付时间。Chien[5]提出了一个基于最优小修次数的备件订购策略，该策略考虑了常规交付时间。Panagiotidou[6]提出了基于库存水平的备件订购策略。Louit等[7]提出了基于组件剩余寿命的订购策略。Godoy等[8]提出了一种利用图形化技术描述的订购策略，该策略考虑了基于状态的可靠性和交付时间。 Wang等[9]提出了一个针对退化系统的视情订购策略。在这些文献中，订购策略涉及的备件大多都是单一组件或简单系统，涉及到复杂系统的订购还不多见。其次，针对高可靠性系统视情订购策略明显优于基于年龄的订购策略，其主要依据系统本身的退化状态进行订购， 而在文献中针对退化系统展开研究的并不多见。最后，文献中也只有极少数学者在订购时同时考虑了常规随机交付时间和紧急随机交付时间。

实际上，复杂系统由一系列的部件构成，而且各部件之间往往存在竞争退化的情况，因此复杂系统的退化过程是一个复杂的、多机理的过程，描述整个系统的性能退化水平是一件极其困难的事情。根据系统的整体性能退化水平开展PR工作同样也是一件具有挑战性的事情。据了解，很少有文献研究复杂系统的PR策略，特别是将复杂系统、退化行为、常规随机交付时间和紧急随机交付时间都考虑其中的订购策略更是少之又少。鉴于此，本文提出了一种基于复杂系统退化机理的订购策略模型，基于状态空间模型采用核主成分分析(kernel principal component analysis,KPCA)方法[10]通过状态子空间最小夹角获得系统的退化水平，采用Gamma过程[11]来描述系统整体性能退化过程。当系统退化水平达到预设的阈值时，系统被认为失效。所提出的复杂系统订购策略模型依赖于系统退化模型和备用系统随机交付时间，该策略模型采用下订时刻作为决策变量。为了解决系统意外失效引起的问题，该策略模型同时考虑了常规随机交付时间和紧急随机交付时间。基于提出的复杂系统订购策略模型，存在一个唯一的使期望费用率最小化的最优下订时刻。本文的目标是在费用率标准下寻求最优的下订时刻。

1　系统描述

本文的研究对象为一个复杂系统，该系统由若干部件组成，每个部件都有其各自的特征性能退化参数，系统的整体性能退化水平由其中关键部件的特征性能退化参数共同来表征。所有的特征性能参数随测量次数会产生一系列性能退化数据。下面通过对性能退化数据的分析来确定系统整体退化过程模型，并依据系统退化过程模型建立订购策略模型。

1.1　系统退化建模

基于状态空间模型[12-13]通过性能退化数据建立的状态特征矩阵X为

(1)

式中,n为性能参数的个数,m为性能退化测量次数。xij表示第i个性能参数在tj时刻的退化测量值(i=1,2,…,n;j=1,2,…,m)。

系统在正常状态下的特征矩阵与退化状态下的特征矩阵具有不同的数据结构,即它们对应到映射的子空间不同。采用KPCA方法提取状态特征矩阵的状态子空间S,即

S=span(ω1,ω2,…,ωr)

(2)

式中,ω1,ω2,…,ωr为由较大特征值对应的正交基向量,r为子空间维数,且r≤m。

假设系统在正常状态下的状态子空间为Ss,在退化状态下的状态子空间为Sd,Ss与Sd之间的差异可通过基向量间的主夹角表示,即

θi=arccosκi,i=1,2,…,r,0≤θi≤π/2

(3)

式中,κi表示基向量内积。用最小主夹角的正弦值来表示系统退化水平[14],即

ρ=sin(minθi),0≤θi≤π/2, 0≤ρ≤1

(4)

假设ρ(t)表示在某一时刻t的性能退化水平,且服从形状参数为Λ(t),尺度参数为β的Gamma分布,随机过程{ρ(t),t≥0}为Gamma过程满足如下性质:

a)ρ(0)=0;

b)ρ(s+t)-ρ(t)～Γ(Λ(s+t)-Λ(t),β),s≥0,t≥0;

c)ρ(t)具有独立增量。

相应的概率密度函数(probability density function,PDF)可表示为:

(5)

累积分布函数(cumulative distribution function,CDF)表示为

(6)

定义首次到达失效阈值l的时间Tl=inf{t≥0|ρ(t)≥l}, 则系统在时刻t的累积失效概率为

(7)

式中,Γ(·)表示Gamma函数,γ(·)表示不完全Gamma函数,即

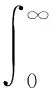
由(7)式,很容易算出系统的期望寿命μTl为

(8)

1.2　假　设

为了使本文的研究合理、有效,作如下假设:

1) 当系统退化水平超过预设的阈值l时,则认为系统失效。

2) 系统在零时刻开始运行。

3) 当系统失效时立即进行紧急订购,即认为系统失效与紧急订购之间的时间间隔为零。

4) 系统的退化水平可以被实时检测到。

5) 由于系统失效会带来许多负面影响,因此认为缺货成本率大于库存成本率,即ρs>ρh>0。

2　订购策略模型

2.1　模型描述

通过CBCM获取当前时刻监测部位的性能退化数据,基于状态空间模型采用KPCA方法获得系统当前时刻整体退化水平,系统所有时序退化水平通过Gamma过程来描述。基于系统退化过程模型,同时结合备用系统随机交付时间制定订购策略,通过期望费用率目标函数求解最优订购时刻。具体模型的执行步骤如图1所示:

图1　订购策略模型

步骤1获取t时刻系统性能退化数据。对系统关键部件进行定期检测,采集各关键部件的特征性能参数退化数据。

步骤2建立特征状态矩阵。基于状态空间模型通过性能退化数据建立特征状态矩阵。

步骤3计算系统性能退化水平。采用KPCA方法提取状态特征矩阵的状态子空间(正常状态子空间和退化状态子空间),通过状态子空间夹角计算出t时刻系统性能退化水平。

步骤4构建系统性能退化过程。根据步骤3计算出当前时刻的系统性能退化水平,重复步骤1～3,得到时序系统性能退化水平,构建随时间变化的系统性能退化过程,该退化过程用常用的Gamma过程来描述。

步骤5构建订购策略。根据系统性能退化过程和备用系统随机交付时间(常规交付时间和紧急交付时间),建立常规订购策略和紧急订购策略。

步骤6订购时刻寻优。通过建立的订购策略,以期望费用率为目标函数,寻找使期望费用率最小时的最优下订时刻。

2.2　订购策略

在订购策略中存在3种互斥和完备的状态,如图2所示。图中T表示当前下订时刻,Lr表示常规交付时间,Le表示紧急交付时间,H表示库存时间,S表示缺货时间,Replacement 表示替换时刻。下面分别对这3种订购策略状态进行描述。在整个订购策略中,会涉及系统退化失效函数和交付时间函数。

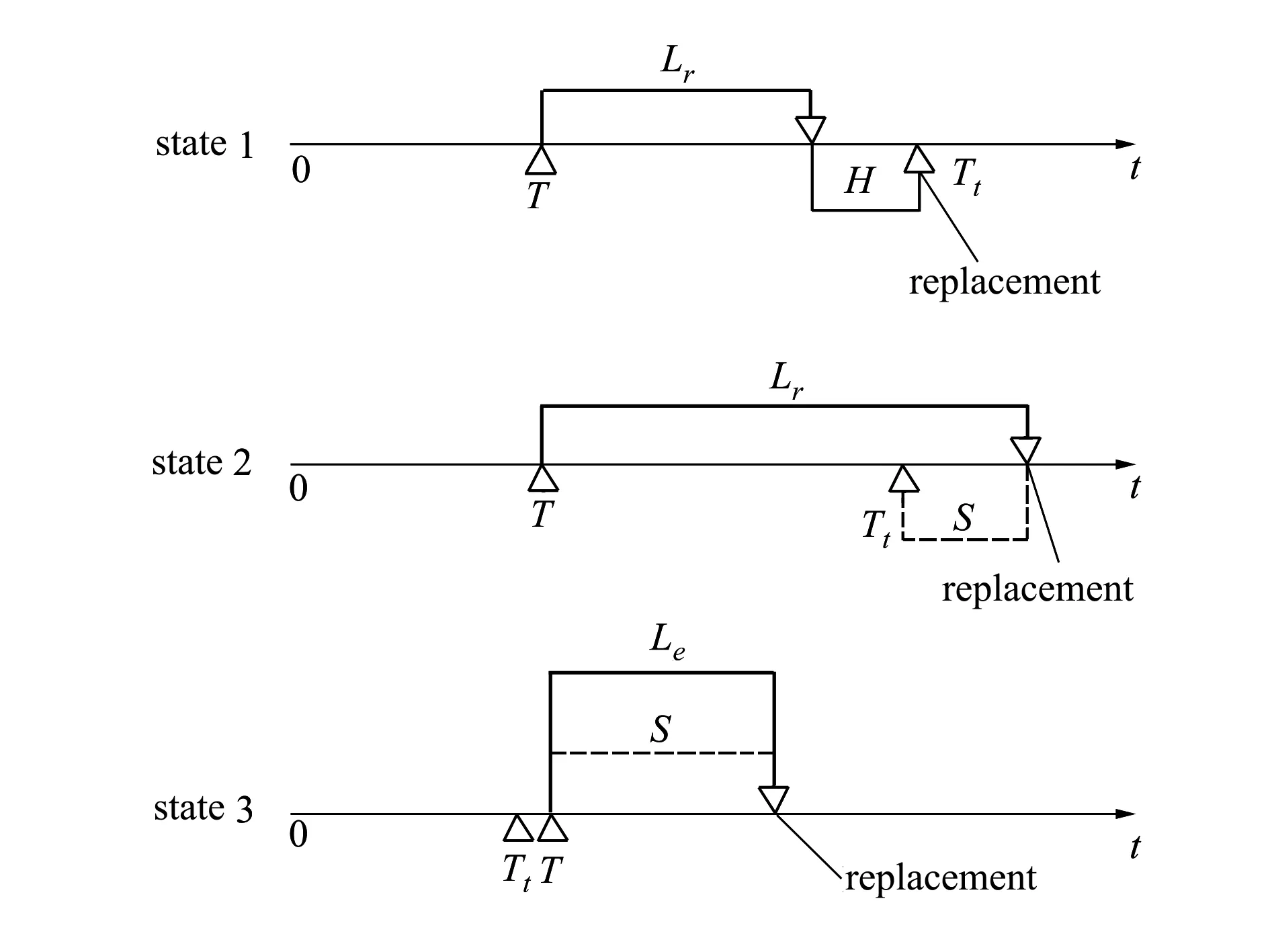
图2　一个周期内的订购替换状态

state1如果下订时刻发生在系统失效之前,且在系统失效之前订购的备用系统到达,那么当订购的备用系统送达时入库,此时的订购采用常规订购,同时会产生库存成本。此状态发生的概率为

state2如果下订时刻发生在系统失效之前,且在系统失效之后订购的备用系统送达,那么当订购的备用系统送达时入库,此时的订购采用常规订购,同时会产生缺货成本。此状态发生的概率为

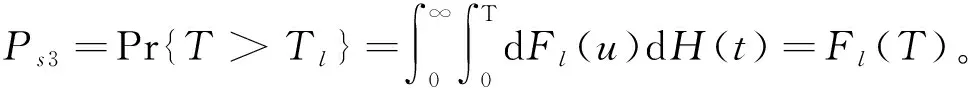
2.3　订购时刻寻优

本小节采用期望费用率作为衡量标准,通过使期望费用率最小化来获取最优的订购时刻。

如图1所示,整个替换周期形式化表达如下:

(9)

式中,U表示替换周期长度。

由于库存时间仅可能发生在state1,因此在替换周期内期望库存时间EH可表示为

(10)

进一步的,由于缺货时间可能发生在state2和state3, 因此替换周期内期望缺货时间ES可表示为

(11)

由于日常监测会发生在所有状态中,因此替换周期内期望监测时间EI可表示为

EI=μTl

(12)

基于以上分析,结合(9)式,期望替换周期长度可表达为

(13)

换句话说,期望替换周期长度也可以由系统期望寿命和期望缺货时间之和来表示。

整个替换周期的成本包括替换成本、常规订购成本、紧急订购成本、库存成本、缺货成本和日常监测成本,即

(14)

式中,C表示替换成本,Cr表示常规订购成本,Ce表示紧急订购成本,ρs表示缺货成本率,ρh表示库存成本率,ρi表示日常监测成本率。

因此,基于更新过程理论[15],单位时间内的期望成本(即期望费用率)可表示为

(15)

式中，EU(T)和EV(T)分别由(13)式和(14)式给出。我们的目标是利用(15)式求出最优的下订时刻T。

3　实例验证

在工程实际中,许多高端装备的诸多系统模块,特别是核心系统模块如高档数控机床主轴系统、航空航天装备发动机系统、风力发电机主轴系统、导弹制导系统等都是由若干部件构成的复杂系统体,这些复杂系统的健康状态对整机的安全运行至关重要。因此,针对复杂系统的退化状态开展有效的订购替换维修工作意义重大。本文所提的系统订购策略模型主要解决由多部件性能退化引起的系统整体退化过程以及基于系统退化过程开展有效订购替换维修工作,为此,采用文献[14]所提供的系统退化实例来验证该订购策略模型的可行性和有效性。将文献中所研究的导弹制导系统视为一个由多部件组成的复杂系统,并开展相应的系统退化过程和订购策略研究。该系统由无线电高度表、雷达装置、陀螺仪、转换开关装置以及电源等关键部件组成,由系统各关键部件性能退化数据(电压值)建立特征状态矩阵,通过KPCA方法提取出状态子空间,并计算当前时刻退化状态子空间与正常状态子空间之间的夹角,根据最小夹角计算当前时刻退化水平,通过时序退化水平构建Gamma退化过程模型,退化模型参数如表1所示。假设订购的备用系统交付时间服从常用的对数正态分布,其常规交付时间PDF为

式中，μ=2.553,σ=0.153;紧急交付时间PDF为

式中,μ=2.297,σ=0.1。相应的图形化表达如图3所示。注意到,这里所用的w(t)和h(t)一般由备用系统供应商来提供。

表1　系统退化模型参数

表2　成本参数(单元：元)

图3　交付时间概率密度分布

接下来,根据性能退化模型和备用系统交付时间函数,求出在期望费用率标准下的最优下订时刻,假设涉及的成本参数如表2所示。图4展示了下订时刻与期望费用率之间的变化规律,由图可知,最优的下订时刻为使期望费用率达到最小时获得,即T*=50.5,CR=1.702 8。由前述所得模型可知,当前系统的期望寿命为μTl=76,常规交付时间期望μr=13,紧急交付时间期望μe=10,再将成本因素、系统寿命误差和意外失效因素、交付时间误差因素等考虑在内,最优的下订时刻T*=50.5是合理的。

图4　期望费用率随下订时刻的变化规律

4　结　论

1)本文分析了复杂系统的退化特点，提出了一种基于复杂系统退化机理的订购策略模型，该系统的退化水平由各关键部件的特征性能退化状态子空间共同来表征，系统的整体性能退化过程由Gamma过程来描述。

2)根据提出的订购策略模型，系统下订时刻依赖于系统退化过程模型和订购策略。通过使期望费用率达到最小，可以方便地寻找到最优的下订时刻。

3)本文提出的方法可以广泛适用于由多部件退化导致的系统整体退化过程和基于该退化过程进行备用系统订购替换维修的活动。

尽管基于所提出的订购策略模型得出了满意的结果，但还需要研究面向服从退化和冲击劣化系统的订购策略模型和多系统订购策略模型，以便获得更高的生产效率和安全保障。