特殊环境下的高精度超声定位误差研究
2018-07-14诸国磊王英民王奇
诸国磊, 王英民, 王奇
(西北工业大学 航海学院, 陕西 西安 710072)
声学定位系统与其他传感器联合以获取载体在水下工作时的更多信息,实现更广泛的水下导航定位已经成为声学定位技术发展的必然趋势。
本文以江门中微子探测项目[1-2]为背景,需要在一个充满烷基苯液体的直径为35 m的球形容器内对小型航行器进行精确定位。由于环境的特殊性,通过光电磁等手段的其他定位方式都不可行,需要采用声学定位系统实现对小型航行器的精确定位,要求平面定位误差有效控制在30 mm以内。
目前国内外研究者进行的水下定位研究主要是在相对较大的海域范围内展开研究[3-4],主要采用各类长基线、短基线、超短基线[5-6]方式进行定位,采用的声信号为低频声信号,通过主动信标发射信号,接收阵采用被动定位的方法,接收到信号后对信标的方位和距离进行判断后给出信标的位置信息,该方法适用于大范围水域,但对距离的测量精度一般在0.5%数量级,该精度无法满足本研究需要的高精度定位的需求(距离精度要求在0.5‰量级)。
与常规的声学定位系统相比,本定位系统的应用环境稳定,温度基本恒定,且在此空间范围内的发射与接收可通过物理连接方式建立统一的时统,这使高精度声学定位具有可行性。本文主要研究了超声定位算法及接收换能器的阵型与定位误差的关系,分析了误差产生的原因,给出了合理的布阵建议。为了验证仿真结果的正确性,进行了水池实验,在一定程度上通过实测的方式对误差进行了验证,最终的实验结果表明,当对测距误差进行有效修正后,实测定位误差情况和仿真分析基本一致,可以控制在30 mm以内。
1 平面阵定位算法
1.1 阵型介绍
设探测器的中心点为直角坐标系的原点,竖直向上为z轴的正方向,水平向东为x轴的正方向,水平向南为y轴的正方向,如图1所示。
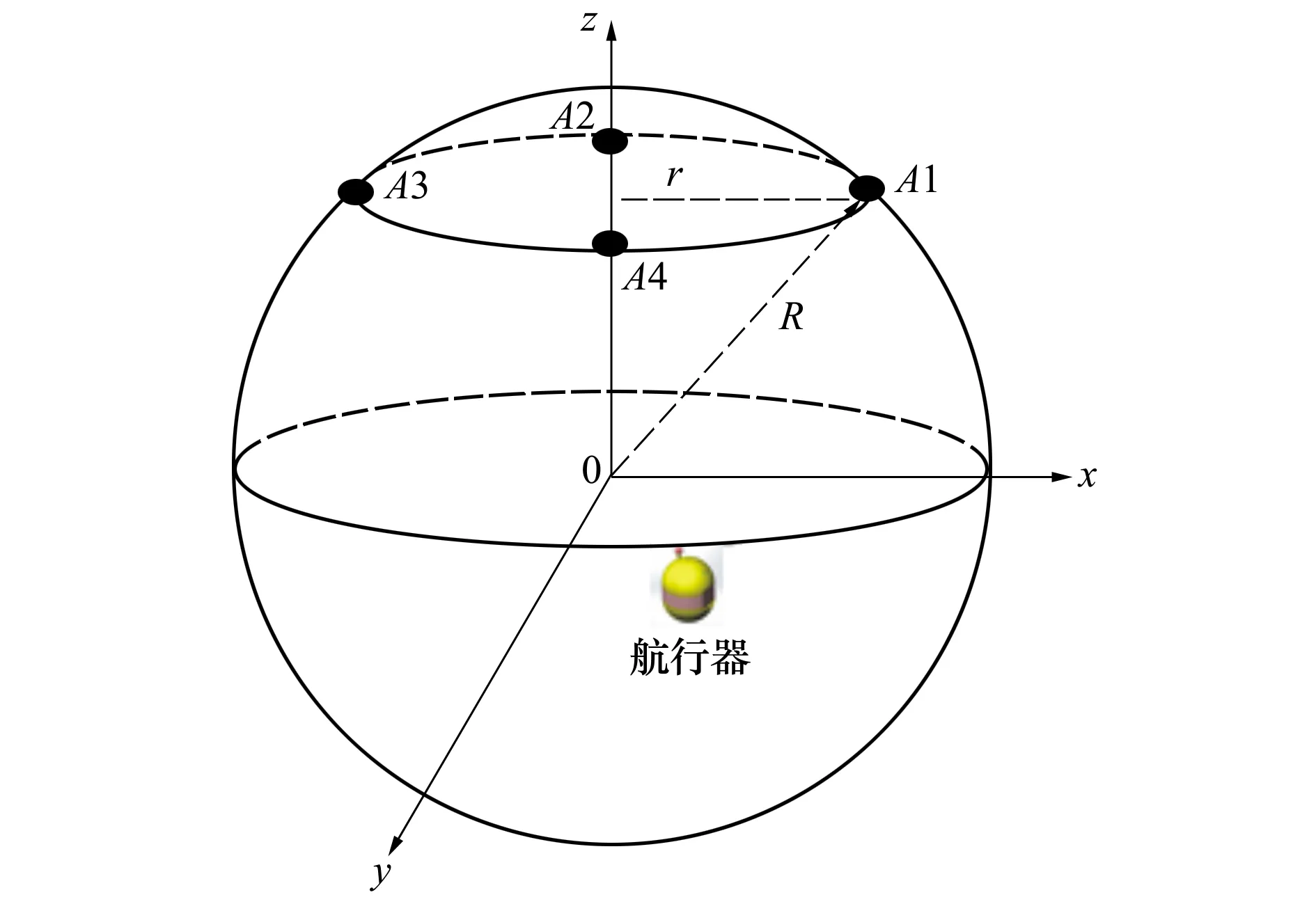
图1 同一平面上四个阵元阵型示意图
接收阵为4个全向水听器构成的平面阵,分别对应A1,A2,A3,A4。R为探测器的半径17.5 m。4个阵元在同一平面的高度上等间距分布,角度分别为0°,90°,180°,270°,平面高度可调,r为阵所在平面半径。
1.2 定位算法
4个阵元的坐标分别为Ai=(xi,yi,zi),i=1,2,3,4,航行器的位置坐标为z1~4,航行器到每个阵元之间的距离可由(1)式给出
(1)
由于接收阵元在同一水平面上(z1~4坐标相同),故对(1)式中每个式子进行两两相减得到(2)式
AX=b
(2)
式中
采用最小二乘算法进行求解,求f(X)=(AX-b)T(AX-b)的极小点即(6)式,就是航行器的x和y的位置坐标。
(6)
航行器z坐标的获取是通过航行器上自带的高精度压力传感器解算获得,其精度可以达到0.1 mm的量级,认为是精确已知的,本文中只分析航行器平面位置坐标(x,y)的定位误差。
目标的定位精度δ(即定位误差)可由(7)式算出:
(7)
式中,(x0,y0)为航行器真实位置坐标,(x,y)为算法解算的航行器位置坐标。
2 误差分析
上述平面阵定位算法,在已知接收阵元位置的情况下,通过多组距离信息解算目标位置。主要误差来源于距离信息的获取。下面对测距过程中产生的误差进行分析。
2.1 测距原理
本文采用的测距基本方法是TOF(time of flight)渡越时间检测法[7]。其基本原理是:声源传感器向外发射声波时刻为ts,接收感器接收到声波到达时刻为tr,根据发射与接收的时间差t=tr-ts来计算声源和接收传感器之间的距离:
d=c·t
(8)
式中,c为传播介质中的声速。
2.2 测距误差
测距的精度既与测量时间差的精度有关,也与用来计算距离的声速值有关。时间差的精度主要受系统参数影响,如超声波频率、超声波传感器和检测电路、定时器使用方法等。而声速主要受环境因素影响,如环境温度、湿度等。下面对引起误差的因素进行定量的计算,得到本文中定位误差分析使用的测距误差。
2.2.1硬件计时精度带来的误差
当单片机晶振频率为6 MHz时,计数频率为晶振频率的1/12,即0.5 MHz,此时计时量化误差为:
(9)
2.2.2声波幅度带来的误差
由于测量距离、超声波的入射角度、声传播介质等方面的不同,使得接收换能器所获得的声波幅度相差很大,由于声波幅度的差异带来的计时误差如图2所示。

图2 声波幅度导致的计时误差
由图2可以看出,在同样阈值条件下,幅度不同的声波的到达时刻存在计时差别t2-t1,波信号频率越高,这种相位误差会越小,导致的计时误差最终会耦合到测距误差中,假设超声波信号频率为100 kHz,取极限值相位差90°时,可得到计时误差为:
(10)
2.2.3声速带来的误差
在探测器的特殊环境下,只考虑由温度带来的声速误差,水中的简化声速公式如(11)式所示,其中T为水的温度:
c=1410+4.21T-0.037T2
(11)
可得到由温度引起的声速误差如(12)式所示:
Δc=4.21·ΔT-0.074·T·ΔT
(12)
若温度的测量误差、或工作时的浮动温度修正误差为0.2℃,工作环境温度为20℃,则声速误差为:
Δc=4.21·ΔT-0.074·T·ΔT≈0.55 m/s
(13)
2.2.4测距综合误差
考虑以上多种误差的综合影响,则超声测距过程中的总体误差如(14)式所示:
(14)

(15)
因此在进行定位误差仿真时,测距最大误差限取0.02 m(20 mm)。
3 定位仿真
针对上述算法,由于测距时间沿会滞后,所以设定测距值为比真实值偏大20 mm内的随机值。使用蒙特卡罗方法进行定位仿真,每个航行器的运动位置的蒙特卡罗次数为100,用MATLAB做了如下仿真:
3.1 固定接收阵大小,调整航行器与接收阵距离
将接收四元平面阵置于探测器内高度17 m的位置,此时四元平面阵的孔径为8.3 m,我们将航行器范围控制在阵的正下方圆柱体范围内,位置高度从-17~17 m,每隔0.1米取一层,对每一层进行了遍历定位仿真,遍历点半径步长取0.1 m,角度步长取1°。
当航行器所在平面高度为17 m(距离接收阵最近时),仿真结果如图3所示,航行器x和y坐标最大误差为7.6 mm。
当航行器所在平面高度为-17 m(距离接收阵最远时),仿真结果如图4所示,航行器x和y坐标最大误差为22.6 mm。
当航行器位置高度从-17 m至+17 m遍历仿真,处于不同深度的航行器在x-y平面上最大误差分布情况如图5、图6所示,图5为10次测量求平均的结果,图6为100次测量求平均的结果,可以看到误差变化趋势都是随着航行器越靠近接收阵误差越小。10次平均后x-y平面上的最大误差基本都可以控制在73 mm以内,100次平均后x-y平面上的最大误差基本都可以控制在23 mm以内。

图3 阵元高度17 m目标高度17 m误差分布图 图4 阵元高度17 m目标高度-17 m误差分布图 图5 x-y平面最大误差分布图(10次平均)

图6 x-y平面最大误差分布图(100次平均)
3.2 固定航行器与接收阵距离,调整接收阵大小
将接收四元平面阵置于探测器内高度0 m的位置,将航行器位置高度设置在-17 m处,分别调整接收阵孔径为9 m,20 m,35 m(最大孔径),对航行器进行定位仿真。
当阵元孔径为9 m时,仿真结果如图7所示,航行器x和y坐标最大误差为7 mm。
当阵元孔径为20 m时,仿真结果如图8所示,航行器x和y坐标最大误差为6.3 mm。
当阵元孔径为17.5 m时,仿真结果如图9所示,航行器x和y坐标最大误差为5.7 mm。

图7 阵孔径9 m,目标高度-17 m的误差度分布图 图8 阵孔径20 m,目标高度-17 m的误差度分布图 图9 阵孔径35m,目标高度-17m的误差度分布图
当阵孔径不断变化时,定位误差的变化情况如表1所示,可以看到误差变化趋势都是随着接收阵孔径的增大定位误差不断减小。

表1 不同孔径阵型定位误差仿真结果
3.3 仿真结果分析
由仿真结果可以看出,航行器x和y坐标误差与阵元水平面的孔径大小有关。孔径越大,x和y的坐标误差就越小,在允许的条件下,应尽量增大阵孔径。定位误差主要源于测距误差,随着航行器距离阵的距离增大,测距误差增大,定位误差随之增加,布阵时应考虑航行器在不同位置时与接收阵元的距离。因此可将阵型设置为球内接正立方体的形式,同时尽可能的增加测量次数以减少随机误差带来的影响,提高定位精度。
4 实验验证
4.1 实验环境及接收阵的配置
为了对定位效果进行验证,在消声水池中进行了实验验证。实验在一个长20 m、宽8 m、深7 m的消声水池中进行,水池6个面都布满消声尖劈。本次实验仅验证了平面阵的定位性能。实验设备连接及布阵位置如图10所示。

图10 设备连接及布阵示意图
实验中共用到4个接收水听器和1个发射换能器,4个接收水听器的布放位置如图10所示,构成了一个基本位于同一平面的矩形接收阵,接收阵长约7 m,宽约6.7 m,发射换能器可以随意更换位置。参考原点位于图中左上角。
4.2 实验过程
在水池中通过光学标定装置实现声源与4个水听器的精确位置布放,得到准确的声源与4个水听器的空间坐标(建立x,y,z坐标),通过定位系统实现对4组距离(声源至4个水听器)的测量。得到4组距离信息后通过水听器坐标进行声源坐标的解算,并与光学标定声源坐标进行比对,获得定位误差信息。保持4个水听器的坐标不变,改变声源的坐标,进行多次定位实验,验证定位效果。实验环境如图11所示。
4.3 实验数据分析
在水池实验中发射换能器的位置更换了6次,4组接收水听器共得到了24组测距结果,每组测距结果都是10次测试平均值,实验中定位系统测距的稳

图11 实验环境图
定性很好,10次测距标准差基本保持在1 mm以内,最大标准差不超过4 mm。
实验时采用定位系统对声速进行了实时标定,标定的声速值为:1 472.80 m/s。测距结果如表2所示,最大测距误差为19.72 mm,有效控制在20 mm以内。
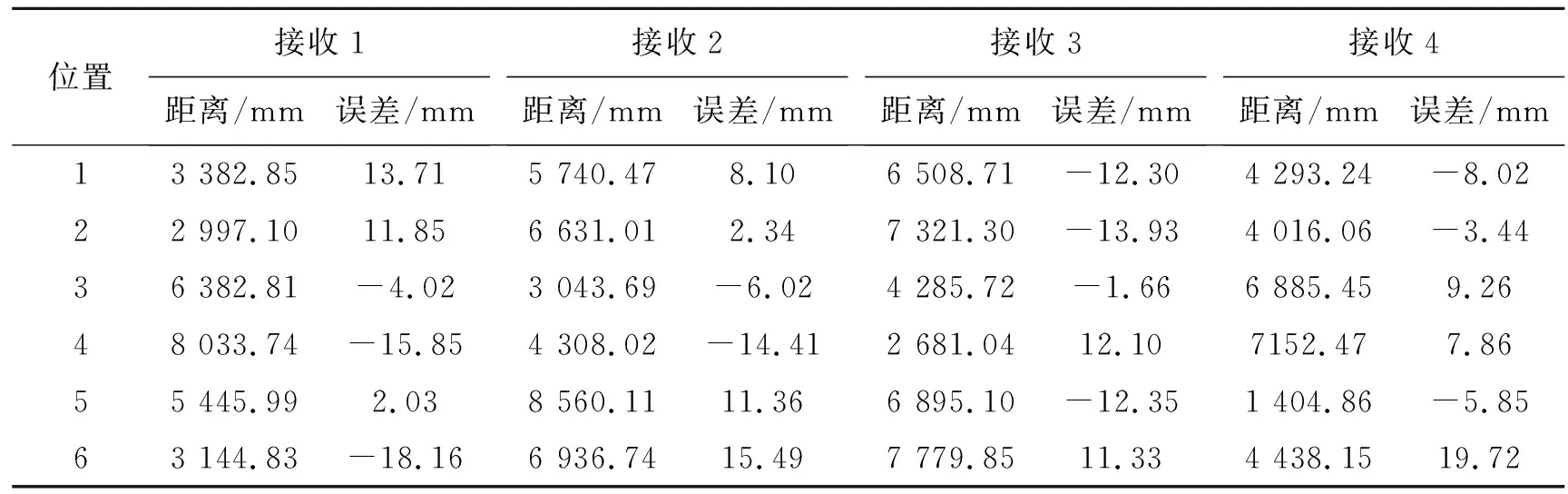
表2 测距误差表
定位结果及定位误差分别如表3、表4所示,其中x,y方向测距和定位精度较高,定位误差控制在30 mm以内,只有一组误差超出,这与仿真结果是基本一致的。

表3 定位结果

表4 定位误差
5 结 论
针对特殊环境中的声学精确定位问题,本文研究了阵型及目标距离对定位精度的影响,仿真了平面阵情况下的定位效果,并进行了水池实验。
从仿真结果和水池实验结果都可看出,定位的精度和超声定位系统的阵型分布以及接收阵与航行器的相对位置有着很重要的关系,当测距误差在20 mm以内,水平孔径达到一定的尺度要求时,水平面上的定位误差可以有效的控制在30 mm以内。
为了满足实际中相对位置及阵孔径大小的需求,建议实际中采用球内接正立方体阵型,此时水平和垂直方向上的阵孔径都可以达到12 m以上,可以保证定位误差小于30 mm。
