双离合器盘毂冲挤成形中的小圆角填充规律研究

张益雷, 胡志力, 李锦, 戴明亮

(1．现代汽车零部件技术湖北省重点实验室，武汉理工大学，湖北武汉430070; 2．汽车零部件技术湖北省协同创新中心，湖北武汉430070)

离合器盘毂成形一直是国内外材料成形所关注的重点之一。近半个世纪,盘毂的成形工艺也在不断变化。从最早的锻造到后来的机械加工,再到摆碾成形,直到更为先进的旋压和冲锻复合成形。相对于其他成形工艺,冲锻复合成形有着更加突出的优势,不仅可以提高产品的成形质量,而且提高生产率,降低生产成本,易于实现产品的更新换代。

在20世纪90年代,日本的中野隆志等人率先开展了板材成形与挤压相结合的复合成形工艺,并把它称之为“FCF工艺”。Wu等人[1]利用有限元软件研究了汽车刹车毂的翻边与镦锻工艺流程,通过评估设计的几种修改方案来确定最佳参数,优化了工艺方案;Mori等人[2]研究了镁合金板材的带小圆角的杯形件的两级冷冲压工艺,先成形一个大圆角的杯形件,然后通过挤压侧壁来减小杯形件的圆角半径;韩国釜山大学Lee等[3]采用冲锻复合工艺,经过9步拉深和3步挤压成形工艺制出了带内齿形的离合器轮毂。Sheu等人[4]使用预成形工艺校正加厚管件的尺寸,通过试验验证了预成形工艺能最小化管件局部增厚的表面缺陷。

华中科技大学王新云等人[5-6]使用冲锻复合成形工艺加工汽车飞轮盘,先冲压出外部形状,然后对需要增厚的部位进行锻造加工,最终获得大厚差成形件。西北工业大学李伟等人[7]提出了粗糙集和改进遗传算法结合共同优化神经网络的方法,试验证明优化后BP神经网络预测精度得到了提高。

现有研究大多关注成形的可行性方面,针对带有齿形等较复杂盘毂类零件成形工艺研究较少,在齿形极小圆角半径的情况下如何提高齿形圆角填充性能及零件成形质量的问题仍未解决。本文根据某汽车双离合器盘毂零件的结构特点,提出一种预成形的方法来生产汽车双离合器内毂零件,结合有限元模拟手段,通过设计合理的坯料预成形形状,在成形齿形过程中促进材料流动,使圆角处尽可能填充完全,提高产品质量。

1　工艺方案

本文研究的零件如图1所示,零件为高度比直径小的开口筒形件,筒壁为等节距齿形结构,齿形筒壁上分布有距筒底高度不等但形状和尺寸相同的腰圆孔,筒底有直径较大的中心孔,零件材料为DC06钢板。零件采用厚度为2.5 mm的板坯成形,齿形侧壁厚度为1.7 mm,减薄率为32%。

图1　零件几何模型/mm

该零件典型制造工艺方案为:下料-拉伸-精整-成形齿形-冲孔-修边、侧壁冲孔。零件成形最大难点在于齿形圆角半径为0.4 mm,圆角半径过小造成材料流动困难而角落难以填充完全。利用deform软件对其成形齿形过程进行有限元模拟,其圆角填充缺陷如图2所示:

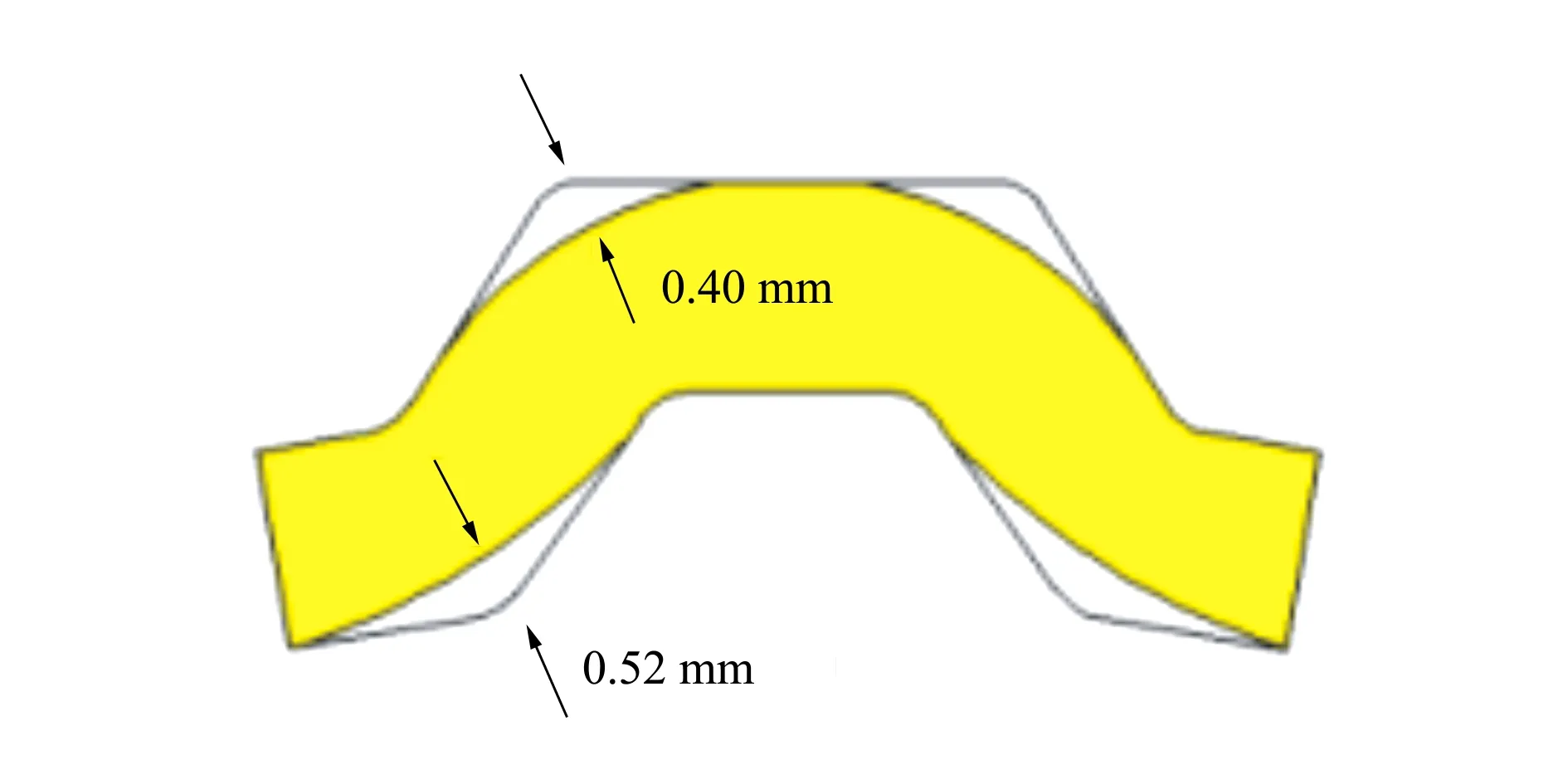
图2　圆角填充缺陷

针对零件小圆角填充困难这一问题,本文提出一种预成形方法,即为了促进材料流动,改善产品质量,将坯料预先制成一定形状,其目的是为了在成形齿形过程中使圆角处尽可能填充完全。冲挤齿形时,选择将预成形件固定在凸模上,凹模自下往上运动完成冲挤成形过程。因此,设计工艺方案为:下料-拉伸-预成形-成形齿形-整形-冲孔-修边、侧壁冲孔,本文主要对预成形到成形齿形及整形过程进行研究,通过分析比较不同形状的预成形坯料对小圆角填充质量的影响,研究预成形坯料几何参数对小圆角齿形填充的影响规律,利用优化算法对预制坯几何参数进行优化,达到提高零件成形质量的目的。

2　内凹式截面促进圆角填充的原理

在材料和壁厚一定的情况下,圆角越小,材料越难以填充。如果将预成形形状设计为内凹形,如图3所示,则可以在圆角较小的情况下较好地使圆角填充完全。其原理是由于中心处坯料内凹,坯料与模具接触面积减少从而使摩擦阻力减小,材料容易向圆角处流动,同时在过渡区附近模具对坯料产生切向推力Fx克服摩擦阻力,促进材料向圆角处流动,切向推力与预成形内凹深度关系密切。对于内凹预成形截面,为方便起见,只取沿零件轴向单位长度一段单元进行受力分析:

图3　受力分析图

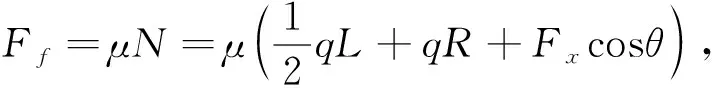
式中,q为模具作用在坯料上的载荷/MPa;μ为模具与坯料之间的摩擦因数；L为波峰间距离/mm；H为内来深度/mm。

在齿形圆角半径较小情况下该切向推力有助于克服摩擦阻力促进材料向圆角流动,使圆角填充完全。

3　预成形形状讨论

根据上面的分析可知,内凹式截面有助于促进齿形圆角填充,因此根据零件特点选择预成形坯料形状如图4所示,坯料下端与零件内齿贴合,坯料上端设计为内凹型,弧ab与弧bc相切,内凹最低点c点距坯料底部上端距离h1、侧壁厚度T和外凸部分两波峰间距离L决定坯料形状。

图4　预制坯形状

为了保证整形时齿形填充完全,既要在内凹处留出足够间隙,又要保证内凹底部距坯料底部上端距离不小于齿形厚度,初步选定h1取值范围为:

1.7≤h1≤1.9(mm)

修正后的预成形方案在原方案的基础上多了一步预成形工序,材料由厚度2.5 mm挤齿成形至1.7 mm,为了使每次成形壁厚减薄率均匀,初步选定侧壁厚度T取值范围为:

2≤T≤2.2(mm)

依据上述几何参数取值范围,内凹型预制坯面积不能大于原有坯料面积,初步选定外凸部分两波峰间距离L取值范围:

4.2≤L≤4.6(mm)

决定内凹型预制坯形状的几何参数包括:内凹最低点距坯料底部上端距离h1、侧壁厚度T和外凸部分两波峰间距离L,不同几何形状的预制坯在冲挤齿形过程中其材料的流动情况不同,对齿形圆角的填充有所影响。下面将讨论这3个几何参数对双离合器内毂成形质量的影响规律。

4　内凹型预制坯成形齿形数值模拟

4.1　有限元建模

零件的几何形状、边界条件和载荷均相对中心轴对称,利用Catia软件对预成形坯料及模具建模,设置好相关参数后生成计算模型提交计算,材料力学性能如表1所示:

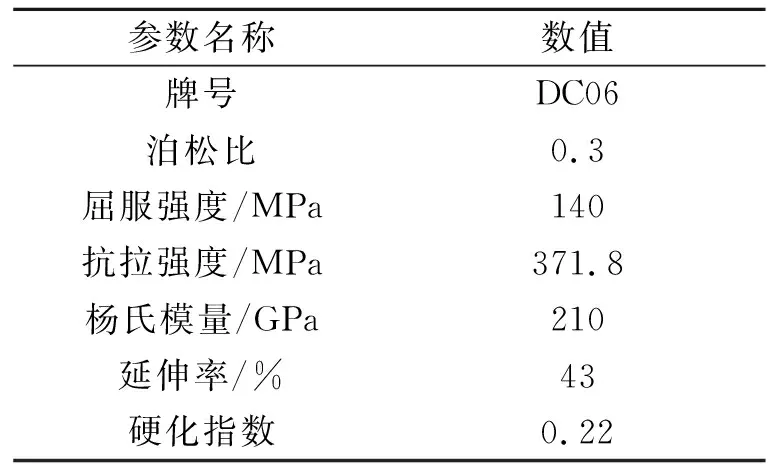
表1　材料力学性能

4.2　预制坯几何参数对成形质量的影响

1) 内凹最低点距坯料底部上端距离h1对成形质量的影响

为了研究h1对成形质量的影响,保持其他几何参数及工艺参数不变,根据上文确定的取值范围,h1分别取1.7,1.8,1.9 mm,观察分析改变h1对齿形圆角填充的影响,使用有限元数值模拟得到相应的齿形圆角填充情况如图5所示:

图5　不同h1的齿形填充情况

由图可知外齿齿顶圆角间隙随着h1的增加而增加,内齿齿根圆角间隙随着h1的增加而减小,说明h1的增加有利于内齿齿根圆角填充而不利于外齿齿顶圆角填充。

2) 侧壁厚度T对成形质量的影响

为了研究T对成形质量的影响,保持其他几何参数及工艺参数不变,根据上文确定的取值范围,侧壁厚度T分别取2,2.1,2.2 mm,观察分析改变侧壁厚度T对齿形圆角填充的影响,使用有限元数值模拟得到相应的齿形圆角填充情况如图6所示:

图6　不同侧壁厚度下的齿形填充情况

由图可知,随着T的增加,外齿齿顶圆角间隙减小而内齿齿根圆角间隙增大,说明T增加有助于促进外齿齿顶圆角填充而不利于内齿齿根圆角填充。

3) 波峰间距离L对成形质量的影响

为了研究L对成形质量的影响,保持其他几何参数及工艺参数不变,根据上文确定的取值范围,L分别取4.2,4.4,4.6 mm,观察分析改变波峰距离L对齿形圆角填充的影响,使用有限元数值模拟得到相应的齿形圆角填充情况如图7所示:

图7　不同波峰距离L下的齿形填充情况

由图可知,随着波峰距离L的增加,外齿齿顶圆角间隙减小而内齿齿根圆角增大减小,说明波峰距离增加有助于促进外齿齿顶圆角填充而不利于内齿齿根圆角填充。

综上分析,预制坯几何参数对齿形圆角填充有一定的影响,且这3个位置处的数值变化对圆角齿形填充的影响是交叉作用的,它们之间的匹配对成形结果有很大的影响, 为了能获得最佳的预制坯几何参数,需要运用优化算法对预制坯几何参数进行优化。下面将结合正交试验设计、BP神经网络(back propagation)和多目标遗传优化算法,即先通过正交试验组合各设计变量,运用有限元对每组方案进行数值模拟计算目标值,然后通过BP神经网络构建优化参数和优化目标之间的映射关系,最终利用多目标遗传优化算法对其进行优化,在变量区间范围内进行寻优搜索,得到最优解并通过有限元模拟对其进行验证,从而达到优化的目的。

5　内凹型预制坯几何参数优化

5.1　BP神经网络建模

基于Matlab构建BP神经网络模型,建立优化参数和优化目标间的映射关系,最终使用遗传算法在变量区间搜寻最优解。

输入层为待优化的预制坯几何参数,输出层为齿形圆角未填充间隙。本文中预制坯几何参数为:内凹最低点c点距坯料底部上端距离h1、侧壁厚度T和外凸部分两波峰间距离L,输入变量即为:h1,T,L。输出变量为:外齿齿顶圆角间隙S1、内齿齿根圆角间隙S2。

数据样本是BP网络学习的依据,本文按照正交设计方法选取数据样本,上文提到的3个输入变量作为试验因素,各因素取3个水平,构造试验因素水平如表2所示:

表2　正交试验因素水平表

根据正交试验的因素水平数,选取L9(34)型正交表,基于deform对正交试验的组合方案进行数值模拟,得到不同组合方案下的外齿齿顶处和内齿齿根处圆角间隙值,如表3所示:

表3　正交试验样本

采用经验公式初步确定隐含层神经元数:

式中,p为隐含层神经元数;m为输入层神经元数;n为输出层神经元数;α为1～10之间的常数。本次计算中m=3;n=2,代入公式求得;p的取值范围是4～13。

BP神经网络中隐含层采用sigmoid型传递函数tansig,输出层传递函数采用线性函数purelin,设定网络训练目标的误差为0.001,学习速率为0.1,设定迭代次数为10 000,当达到最小误差要求或迭代次数时训练终止。

不同隐含层神经元数情况下BP网络的拟合精度如表4所示,当隐含层神经元数为8个的时候误差值最小,说明此时拟合精度较高,因此选定隐含层神经元数为8个。

表4　不同隐含层神经元数的均方误差

5.2　多目标遗传算法建模

多目标遗传算法建模包括设计变量选取、约束条件和目标函数确定三部分,上文中基于BP神经网络构建预制坯几何参数和齿形圆角间隙之间的映射关系,结合训练后的神经网络利用遗传算法构建多目标优化设计模型,所建立的数学模型为:

式中,h1为内凹最低点距坯料底部上端距离;T为预制坯侧壁厚度;L为预制坯外凸波峰间距离;T为外齿齿顶圆角间隙;L为内齿齿根圆角间隙。

5.3　基于Pareto解的多目标遗传算法优化

本文采用NSGA-Ⅱ算法,遗传算法的目标函数为经过训练的BP网络,使用多目标遗传算法进行寻优,得到包含非劣解的Pareto最优解如表5所示。

表5　基于遗传算法获得的Pareto最优解集

从表中可以看到,10组最优解组成了Pareto最优解集,需要从最优解集中挑选一组满意解作为预制坯最佳几何参数以及最优目标值。本文使用满意度函数的方法来挑选满意解,满意度函数值越大,表明目标值越优。满意度函数为:

式中,f1max,f1min分别为Pareto最优解集中f1的最大及最小值;f2max,f2min分别为Pareto最优解集中f2的最大及最小值。

通过对各组Pareto最优解满意度进行计算,其满意度函数值如表6所示:

表6　Pareto最优解集的满意度值

从表中可以看到,最优解集中第10组目标值的满意度函数值最大,说明由其对应的预制坯得到的双离合器内毂小圆角齿形填充效果最好,故将该组作为满意解。其对应的预制坯几何参数为h1=1.843 9 mm,T=2.124 8mm,L=4.567 8mm,保留2位小数,即h1=1.84 mm,T=2.12 mm,L=4.57 mm。

为了对优化结果的准确性进行验证,探讨BP网络结合多目标遗传优化算法是否有效,在最优解情况下基于Deform进行冲挤齿形有限元模拟,优化后齿形填充效果的对比如图8所示,

图8　优化前后盘毂成形质量对比

优化后的齿形填充效果明显得到了改善,内齿齿根处圆角间隙为0.09 mm,外齿齿顶处圆角间隙为0.10 mm,满足工件的精度要求。

图9　试验结果

图9所示为采用优化参数组合进行试制得到的零件,由图可以看到零件小圆角齿形填充较好,成形质量高。试验结果与模拟结果基本吻合,验证了工艺方案的可行性和模拟结果的准确性。

6　结　论

1) 根据某双离合器内毂小圆角齿形填充困难这一技术难题,提出了预成形工艺,通过受力分析可以知道,将预成形坯料制成内凹型可以促进金属向圆角处流动以填充齿形。

2) 通过将坯料预制成内凹型促进小圆角齿形填充,其原理一是坯料与模具接触面积减少从而使摩擦阻力减小,同时在过渡区附近模具对坯料产生切向推力FX克服摩擦阻力,促进材料向圆角处流动。原理二是坯料侧壁壁厚减薄有利于侧壁处金属向圆角处流动,促进圆角填充。

3) 在内凹型预制坯几何参数中,内凹最低点距坯料底部上端距离h1的增加有利于内齿齿根圆角填充而不利于外齿齿顶圆角填充,侧壁厚度T增加有助于促进外齿齿顶圆角填充而不利于内齿齿根圆角填充,波峰距离L增加有助于促进外齿齿顶圆角填充而不利于内齿齿根圆角填充。

4) BP神经网络结合多目标遗传优化算法能够有效地对预制坯几何参数进行优化,内凹最低点c点距坯料底部上端距离h1、侧壁厚度T和外凸部分两波峰间距离L最优取值分别为:1.84,2.12,4.57 mm,优化后齿形圆角填充性能得到了改善,提高了双离合器内毂的成形质量。

5) 根据最优工艺参数进行试制,得到的成形件质量较好,试验结果和模拟结果基本吻合,验证了此工艺方案的可行性。