单桩-土相互作用非线性数值分析模型
2018-07-13刘亚明司炳君
刘亚明,司炳君,何 福
(1.大连理工大学建设工程学部,辽宁大连 116024;2.防灾科技学院防灾工程系,河北三河 065201)
0 引言
桩基础是桥梁工程中常用的基础形式,但由于埋置于地下,强震后其破坏形态难以评估。而在地震作用下,桩-土之间会产生一系列接触、分离、再接触等复杂力学行为,进而对上部桥梁结构安全产生不利影响。汶川地震后,诸多桥墩发生了严重的倾斜破坏,但墩身本身震害并不严重,是否由于桩-土间的非线性反应引起了墩顶的残余位移值得关注[1]。因此,桩-土之间相互作用一直是桥梁抗震领域中热点问题,国内外诸多学者对其进行了积极探讨。
Penzien等[2]提出土-桩-桥梁结构相互作用集中质量分析模型,模型中将土与结构简化为多质点系,桩-土之间相互作用由水平桩土相互作用弹簧和阻尼器表示。该模型只适用于单桩结构,且地震波输入较为复杂,因此具有很大的局限性。孙利民等[3]对Penzien模型进行了改进,改进后的Penzien模型增加了自由场对群桩的影响,并且改进了地震动的输入方式,很好地弥补了Penzien模型必须在计算之前首先计算各层土体地震动输入的不足。El-Naggar等[4-5]提出了动力Winkler地基梁模型,模型中考虑了土体的非线性、桩-土界面的不连续性和不同类型阻尼的能量耗散,该模型适用于单桩动力分析与群桩结构的计算。Nogami等[6]建立了桩土相互作用基本模型,在此基础上,发展了非线性时域动力Winkler地基梁模型,模型由近场单元与远场单元两部分组成:近场单元通过滑动单元以模拟桩-土之间的滑移效应;远场单元则用于模拟非线性较弱的远场土体力学特性。
目前我国规范中采用m法来考虑桩-土之间的相互作用,认为桩-土之间是连续的弹性介质,未考虑桩-土之间相互摩擦等复杂的非线性特性。为讨论弹性理论计算方法对模型试验的适用性,王涛[7]将一系列的模型试验结果与弹性理论分析结果进行对比,发现弹性理论方法夸大了桩-土之间的相互影响,导致桩身沉降计算值偏大以及桩顶反力分布的不均匀。王立忠等[8]通过数值分析方法分别建立了非线性、弹性桩-土-桥墩分析模型,并进行Pushover分析与非线性时程分析,认为结构在发生轻微损伤时,相对于非线性桩土模型,弹性桩土相互作用模型过于保守。王常峰等[9]提出了经过试验验证的双向、单向双线性弹簧模型来模拟桩-土之间接触-分离双重非线性行为。在此基础上,张永亮等[10]发展了三线性弹簧模型,更精细地考虑了桩土之间的非线性相互作用。
本文借助OpenSees数值分析平台,建立了桩-土相互作用非线性数值分析模型,模型中考虑了桩-土之间水平相互作用与桩身的非线性特性。结合拟静力试验结果,验证了模型的准确性,为桩基础的地震破坏机理分析及抗震设计提供有益的参考。
1 数值模型建立
1.1 材料本构模型
桩身混凝土数值模型用Concrete01,它是基于Kent-Scott-Park的单轴混凝土本构模型发展而来。其受压应力-应变关系如图1所示,该模型可考虑混凝土因箍筋约束而产生的强度提高及峰值应变增大的特点,不考虑混凝土的受拉应力及刚度,加卸载采用Karsan-Jirsa线性准则。钢筋材料采用Steel02模型,其应力应变关系呈双线性,是基于Giuffre-Menegotto-Pinto模型发展而来。该模型主要组成参数为:钢筋屈服强度、钢筋弹性模量、钢筋屈服后弹性模量强化系数b(文中取为0.001)以及控制钢筋由弹性进入塑性的三个重要系数R0、CR1、CR2。模型中,R0、CR1、CR2采用OpenSees用户手册中建议值,分别取值为15、0.925、0.15。
1.2 桩-土相互作用
在循环荷载作用下,单桩结构的桩侧竖向摩阻力与桩尖土土体抗力对结构的侧向反应影响较小[11]。因此,为简化分析,桩-土相互作用仅考虑桩侧土的水平抗力。
桩-土水平相互作用通过p-y弹簧模拟,以OpenSees中的PySimple1材料考虑。该材料主要由3个参数Pult、y50、Cd确定,其中,极限土抗力Pult,由式(1)与式(2)中较小值确定[12],计算所得的单位为kN/m,因此还需对上述结果乘以单位桩长;土体抗力达到极限承载力-半时桩身变形量y50,可通过API中砂土力-位移关系式来推导,具体见式(9)~式(10);最大阻力与极限土抗力Pult的比值Cd,文中取OpenSees用户手册中建议值0.3。
pult=γz[z(P1+P2+P3)+D·P4]
(1)
pult=KaDγz(tan8β-1)+K0Dγztanφtan4β
(2)
(3)
(4)
P3=K0tanβ(tanφsinβ-tanα)
(5)
(6)
式中,P1、P2、P3、P4为简化计算公式而引入的参数,无具体含义;γ为土体有效重度;z为桩的入土深度;Ka为最小主动土压力系数,由式(7)确定;K0为静止土压力系数,取为0.4;α、β为与砂土相关的系数,计算公式为式(8);φ为砂土的内摩擦角,计算时应换算为弧度;D为桩身直径。
(7)
α=φ/2;β=45°+φ/2
(8)
这里需要注意的是,由上述公式计算所得的土体极限抗力未考虑循环荷载作用下土体抗力衰减的现象,这与实际情况不符。因此,需对计算所得的土体极限抗力乘以折减系数A。根据API规范[13]可知,循环荷载作用下A取0.9。对地表处的土体抗力而言,由式(1)与式(2)计算所得的土体抗力值为0,不符合实际,由此在模型中地表处的土体抗力按照单位桩长的一半进行计算。
(9)
(10)
式中,k为地基刚度系数,其取值通过ATC-32[14]中建议的确定,文中取为22000kN/m3。
1.3 数值分析模型
如图1(a)所示,位于地表之上的自由段桩长采用基于力的纤维梁柱单元来模拟;位于地表以下的桩身采用基于位移的纤维梁柱单元模拟[15]。地面以下的桩身按长度等分为27份,约束桩底竖向自由度。图1(b)为桩身截面布置示意图。图中阴影部分为保护层混凝土,保护层厚度为50mm。桩身截面由三部分组成,分别为40根保护层混凝土纤维、200根核心混凝土纤维以及7根纵向受力钢筋纤维(因后文的试验中纵筋为7根)。沿桩身高度水平方向布置有p-y零长度弹簧单元,以模拟桩-土之间的相互作用。p-y弹簧单元初始长度均为0,组成弹簧单元的两个节点具有相同坐标,其中一端节点固定,另一端节点与桩身水平方向自由度耦合。

图1 桩-土相互作用数值分析模型Fig.1 Numerical analysis model for pile-soil interaction
2 数值模型的验证
为验证模型的准确性,选取Chai和Hutchinson[16]完成的单桩拟静力试验结果进行对比。其1号桩桩径D为406mm,地面以上自由段长度为2D,土体埋深13.5D。截面配有7根直径22mm的钢筋,屈服强度为421MPa,对应配筋率为2.1%。箍筋直径5.4mm,竖向间距50mm,屈服强度710MPa。混凝土的实测抗压强度为41MPa。试验采用力-位移混合加载方式,并于桩顶施加445kN的竖向荷载,对应的轴压比为0.1。土体采用密实砂土,实测土体有效重度为18kN/m3,相对密实度Dr=81%,内摩擦角φ为44°。
图2为桩顶滞回曲线、骨架曲线的试验结果和模拟结果对比图。可以看出,数值分析结果与试验结果吻合较好。试验得到的桩顶初始侧向刚度(正负方向均值)为3.06kN/mm,模拟值为3.25kN/mm,相差5.7%。极限荷载(正负方向均值) 试验值为130.37kN,模拟值为125.65kN,相差3.6%。且模拟结果很好再现了桩水平抗侧刚度的退化行为,表明采用p-y弹簧法来考虑桩土相互作用的方法是可行的,验证了模型的准确性。

图2 模拟与试验滞回曲线、骨架曲线对比Fig.2 Comparisons between the numerical and test results of the hysteretic and skeleton curves
3 土体反应分析
为进一步认识模拟水平地震荷载作用下不同深度处土体的响应,各深度处砂土水平力-位移关系曲线如图3所示。由图3可知,在地面以下4倍桩径深度范围内,砂土在循环加载过程中表现出明显的非线性特征。且随着土体深度由0.5D增大至3D时,土体的变形值逐渐减小,土体水平力不断增加,土体初始刚度逐渐减弱。直至地下6倍桩径处,土体表现为线弹性,且土体变形值明显减弱。
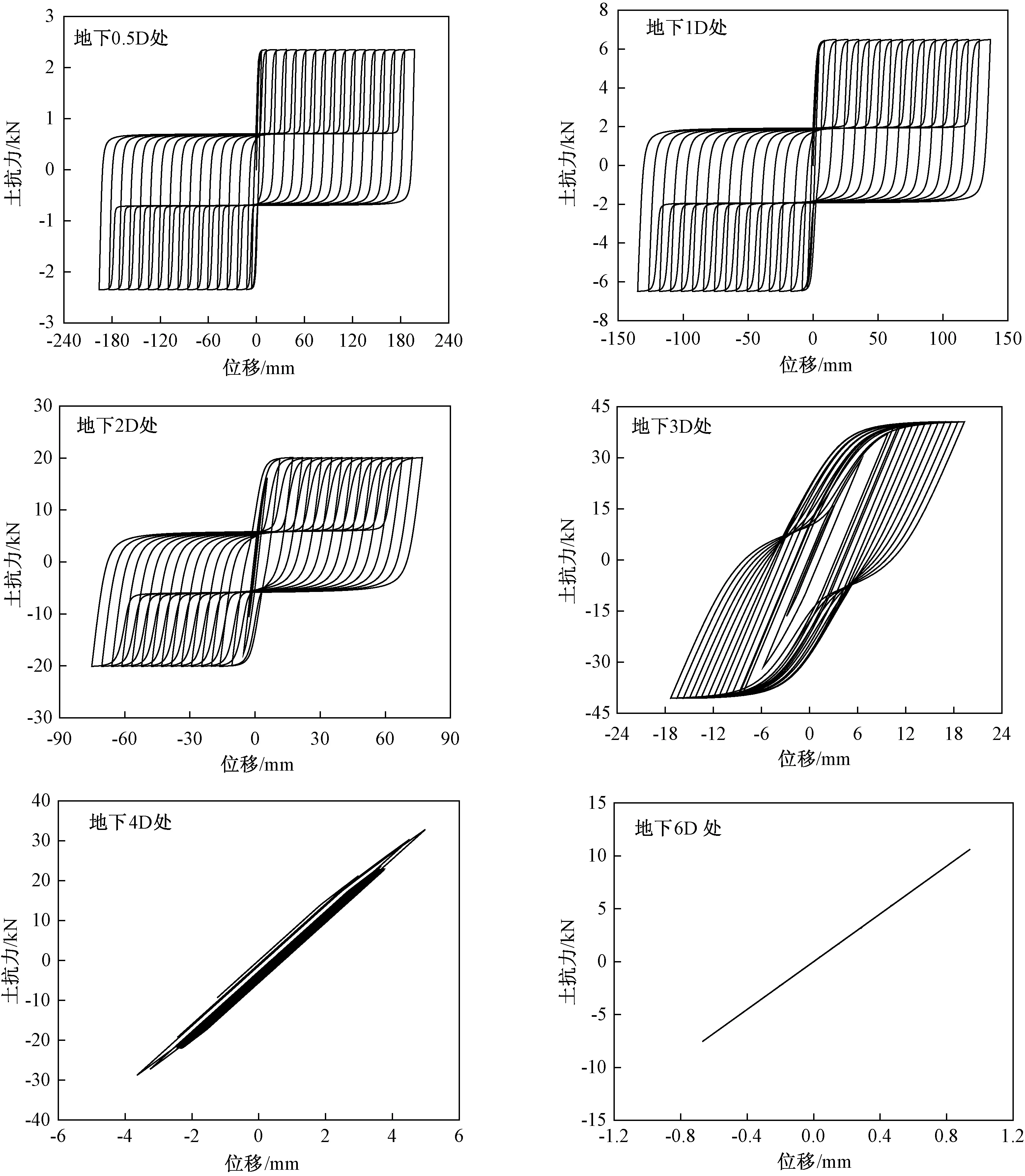
图3 不同深度土体水平力-位移关系图Fig.3 The relationship between soil horizontal force and displacement in different depth
4 结论
本文通过OpenSees数值分析平台建立了桩-土相互作用数值分析模型,在验证模型准确性的基础上,分析了不同深度土体的反应,主要结论为:
(1) 基于OpenSees数值模型模拟得到的桩顶水平力-位移滞回曲线、骨架曲线均与试验结果吻合较好,验证了模型的准确性。
(2) 由模拟得到的砂土抗力-位移曲线可知,在循环荷载作用下,地下0.5~4倍桩径深度内砂土水平力学性能均表现出明显的非线性特征,直至地下6倍桩径处,土体表现为线弹性。
