大跨径人行钢悬索桥动力特性研究

彭　伟

(1.重庆安济建设加固工程有限责任公司，重庆　401120； 2.招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆　400067)

0　引言

现代悬索桥是由主缆、吊索、桥塔、加劲梁、锚碇等组成的结构，主缆是其主要承重构件，通常采用高强镀锌钢丝或镀锌钢丝绳。在恒载作用下，主缆初始张拉力能对结构提供强大的重力刚度[1-2]，降低对桥塔和加劲梁的抗弯刚度要求，加劲梁截面无需随跨径增加而增大。这种特性使悬索桥成为跨越能力最强的桥型[3]，能满足在宽阔水域或深沟峡谷建设大跨桥梁的需求，并诞生了金门大桥、明石海峡大桥、江阴长江大桥、香港青马大桥等主跨超千米的悬索桥。

由于使用对象与公路悬索桥不同，人行悬索桥是一种相对特殊的结构形式[4]。缆索材料以钢丝绳为主，桥塔高度有限，桥面宽度与加劲梁高度都较小；出于经济性和施工考虑，加劲梁一般采用型钢纵横梁，而不是抗弯性能更好的钢箱梁或钢桁梁，但型钢纵横梁自重小，难以有效补充结构整体刚度。这种构造上的差异，使人行悬索桥整体刚度不足，动力特性更复杂。

人行桥的动力特性是影响结构服役性能的重要因素[5-6]。受制于相关规范的空缺，我国人行悬索桥在设计和运营阶段往往重视承载能力评价，并没有充分考虑结构动力特性及行人过桥时的振动问题，这不仅引起结构安全隐患，也造成较差的结构使用体验。了解结构动力特性是改善动力性能的基础和前提，本文以在役人行钢悬索桥为背景进行动力特性计算分析及现场测试，综合评价结构动力特性后提出改进措施，相关结论可供类似人行钢悬索桥今后设计参考。

1　结构动力特性分析方法

结构动力特性是结构本身的固有参数，包括自振频率、振型及阻尼比等[7]，这取决于结构型式、刚度与质量分布等因素。目前，获取结构动力特性的方法主要有理论计算与试验测试两大类。

1.1　计算分析

基于结构动力学理论的动力特性计算主要有解析法和数值法[8]。为获得影响结构动力性能的主要因素，对结构进行充分简化后，解析法通常按单自由度或有限自由度的简化模型进行计算。随着有限元理论和结构电算工具不断进步，对实际自由度远大于1的工程结构，采用接近实际的力学模型进行数值计算是更为简便实用的做法。

根据结构振动数值计算理论，利用动力平衡关系，结构自由振动方程为：

(1)

如果无附加耗能减振装置，实际结构自身的阻尼很小，忽略阻尼力项并代入特解，得对应的特征方程：

(K-ω2M)X=0

(2)

为使特征向量X的n个分量不全为零，特征值应满足频率方程：

Δ(ω2)=|K-ω2M|=0

(3)

1.2　试验分析

由于结构存在损伤或病害，在役结构的材料性能、构件连接状态等与设计情况难免有差别，结构理论计算结果与真实情况可能有差异，而且结构的阻尼水平与实际耗能能力直接相关，一般只能通过试验进行测定。因此，试验测试分析对合理评价在役结构动力特性具有重要意义，既可修证理论计算结果，也为结构安全评估及运营养护提供必要的实际数据资料。

用试验方法获取结构动力特性，首先应使结构发生振动，通过传感器采集不同测点的振动信号并进行频域或时域分析[7,9]，最终得到自振频率、阻尼比等信息。根据不同起振方式，可分为强迫振动试验与脉动试验，前者一般采用突加荷载、突卸荷载或突然释放初位移等方式使结构产生自由振动，后者利用环境各种激励引起结构产生的微小振动(脉动)，由于结构脉动信号图可视为结构各阶频率谐合而成，对脉动记录进行频谱、功率谱或传递函数分析，便可确定结构动力特性。在实际测试中，应根据结构对象与试验条件，采用不同的激振方式。

2　工程概况

某跨河人行桥平面呈一字形，东西向对称，由钢结构悬索桥与接地梯步构成(图1)。原设计荷载为人群3.0kN/m2，主跨L=100m，主缆矢高f=8.33m，垂跨比f/L=1/12，两岸设辅助索且水平倾角为21°。加劲梁由型钢纵横梁上下叠合而成，上层纵梁用等边角钢加强横向联系(图2)。主缆与吊索均采用钢芯钢丝绳，主缆横向间距为2.5m，吊索纵向间距2.0m。两岸采用钢筋混凝土桥塔，塔高16m，塔底、锚碇都采用嵌岩桩基础，1#、2#塔与加劲梁间分别采用活动、固定支座。桥面由桥面板与钢质栏杆组成，桥面板为4mm厚花纹钢板，横向净宽2.0m。

图1　人行钢悬索桥立面图 (单位:cm)Fig.1　Elevation of steel suspension footbridge (unit: cm)

图2　加劲梁全景图Fig.2　Panorama of stiffening girders

该桥已运营8年，前期调查表明，除缆索防护层多处破损脱落、钢梁表面局部明显锈蚀及部分连接螺栓松动、桥面钢板多处锈蚀与局部缺焊等外观病害外，结构的振动病害也较突出，尤其当多人过桥时，桥梁有明显振动。对于这种非临时性人行桥，由于桥梁跨径大、宽跨比与高跨比都较小，从合理判断结构整体刚度与服役性能角度，本文对其进行结构动力特性分析测试，为结构动力性能改进及维修处治建立基础。

3　桥梁动力特性计算结果及分析

3.1　动力计算模型

根据该桥竣工资料，尽量准确考虑结构刚度与质量分布情况，基于Midas/Civil软件建立主桥有限元模型进行动力特性分析。

结合悬索桥受力特点与该桥构造和构件连接情况，采用梁单元模拟桥塔及加劲梁，采用桁架单元模拟主缆、辅助索、吊索，主缆按吊索间距划分单元，并考虑几何非线性的影响。现场调查表明，桥面无铺装层，钢板表层已大面积锈蚀，局部有明显的翘曲变形，板间纵向接缝处及板与纵梁连接处都有缺焊或少焊现象，因此，计算中将栏杆、桥面钢板折算为线质量后施加在梁单元节点上。加劲梁与桥塔下横梁之间、主缆与塔顶之间分别采用主从约束模拟；由于基岩埋深较浅，辅助索端部、塔底均按固结处理。

对于钢纵梁与钢横梁，分别依据所用槽钢与角钢的牌号进行材料和截面特性取值，主缆与吊索材料参数取值见表1。

表1　缆索材料参数取值

3.2　结构计算频率与振型特征

对结构有限元模型进行平衡状态分析后，通过实特征分析得到结构各阶自振频率与振型，前5阶振型图及频率见表2。从结构计算频率与振型图可见：该桥前5阶计算频率小于1Hz，频率值低、振动模态密集，这是柔性结构动力特性的典型表现；前5阶振型均以加劲梁横向或竖向振动为主，且一阶侧弯比一阶竖弯更早出现，这表明桥跨结构刚度较小，且横向弯曲刚度较竖向弯曲刚度更弱；前5阶未见扭转振型，表明结构扭转频率较高。

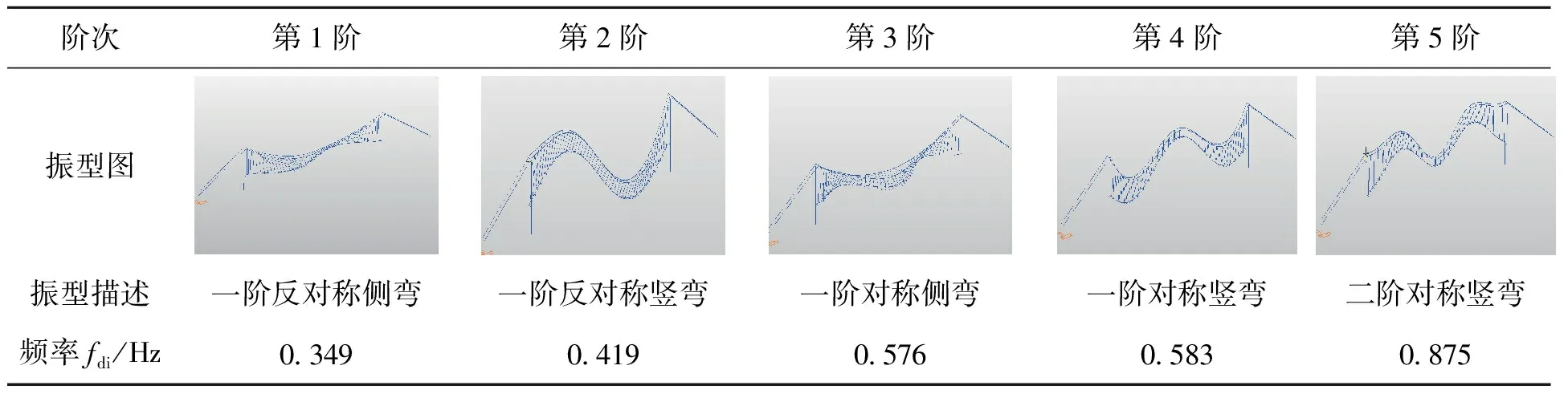
表2　结构计算频率与振型特征

4　实桥动力特性测试结果及分析

4.1　动力测试方案

为进一步了解人行钢悬索桥的动力特性，除上述数值分析外，对实桥进行动力测试以获取结构自振频率与阻尼比。

由于测试对象是人行桥，现场不能采用公路桥的载重汽车突然制动法或模型试验的敲击锤法等方式使结构起振，本文采用脉动法进行动力测试。参考上节各阶振型计算结果，为避免丢失测试模态，测点选择尽量避开前几阶振型的节点，最终选取测点如图1所示，分别位于D1-D1截面(全桥跨中)、D2-D2截面(距1#塔L/8)，在测试截面表面布设国家地震局工程力学研究所研发的941B型高灵敏度拾振器(图3)，具体测试流程见图4。

图3　拾振器布置示意图Fig.3　Layout sketch map of vibration sensors

根据脉动分析原理，脉动记录不应存在干扰信号，测量中应避开其他有规则振动的影响，本文选择气温较稳定、桥面无行人且附近无其它振源情况下进行动态数据采集。

图4　动力测试流程图Fig.4　Flow chart of dynamic test

4.2　实测自振频率与阻尼比

按上述测试方案，各测点实测竖向、横向振动信号幅值谱见图5～图6，对其进行数字滤波、频谱分析后，可得该桥前5阶振型对应的实测自振频率与阻尼比(表3)。

图5　实测竖向脉动频谱图Fig.5　Vertical pulsating spectrum by test

图6　实测横向脉动频谱图Fig.6　Transverse pulsating spectrum by test

表3　结构实测频率与阻尼比

根据实测结果，结构前5阶横向、竖向振动频率密集且位于低频范围内，横向、竖向振动基频分别为0.517Hz、0.757Hz，竖横向基频之比为1.464，表明桥跨结构横向整体刚度低于竖向刚度，这符合大跨径、窄桥面人行桥的一般动力特征；除第1阶振型外，其它阶振型阻尼比均小于3%，但高于CJJ166-2011《城市桥梁抗震设计规范》[10]对悬索桥阻尼比的建议值，由于结构阻尼存在不确定性，阻尼值随测试激励强度或结构振幅的增加而增大，因此，钢结构人行悬索桥振动阻尼比取值还需更多的试验研究。

5　人行钢悬索桥动力特性评价与改进

5.1　结构动力特性评价

根据上述计算与测试结果，可见该桥是具有明显的柔性结构动力特征，低频范围(<1Hz)的振动模态密集，振型特征表现为加劲梁横向或竖向振动为主，这主要是由于结构整体刚度较小所致。

鉴于我国目前没有针对人行桥管养与技术状况评估的规范，本文参照《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)对结构自振频率进行评定。通过对比该桥前5阶自振频率的实测值fmi与计算值fdi，fmi/fdi=1.48～2.93，均大于1.1(相应评定标度为1)，表明结构实际刚度大于理论设计值。

由于型钢纵横梁是人行悬索桥常用加劲梁型式，对比主梁采用钢箱梁、钢桁梁的人行桥[11-12]，除结构形式不同，后者因主梁高度和截面刚度较大，其动力特性明显优于以大跨径、窄桥面、小梁高为结构特征的人行钢悬索桥。

5.2　结构动力特性改进措施

根据我国《城市人行天桥与人行地道技术规范》(CJJ 69-95)[13]，要求人行桥上部结构竖向自振频率大于3Hz，但对横向固有频率未作规定。参考德国最新关于人行桥敏感频率范围评价准则[14]，竖向或纵向振动的敏感频率范围为1.6～2.4Hz，横向振动的敏感频率范围为0.5～1.2Hz，当人行桥的自振频率在上述敏感范围内时，在行人激励下可能会引起较大的振动，增加行人过桥时的不安全感，典型案例如英国伦敦千禧桥(Millennium Bridge)建成当天因大量行人过桥产生较大的横向振动而被迫关闭。对于本文实例，上述实测结果表明结构竖向(0.757Hz)、横向(0.517Hz)基频较低，均不满足文献[13-14]的要求，容易发生振动病害，对此探讨改进结构动力特性的措施。

理论上增大刚度可以提高结构自振频率，由于频率是刚度的二次方根，2倍频率意味着4倍刚度。对于振动基频<1Hz的大跨径人行悬索桥，若完全避开敏感频率范围，需要刚度增加的倍数更多，实际中显然难以实现如此大的刚度增幅，而且提高刚度往往伴随增大结构质量，又引起承载能力问题。根据本文桥例上部结构现状，若不改变矢跨比，可以采用构造措施适当提高结构刚度：在跨中设置中央扣连接主缆与加劲梁，或者加密桥面栏杆立柱，在跨中区段将立柱与主缆固结[15]；增大桥面钢板厚度，加强板间纵向接缝及钢板与上纵梁的焊接，并增设桥面铺装层，减少桥面不平整的影响。

鉴于大跨径人行悬索桥难以调整结构刚度以避开敏感频率范围，为改善结构动力性能，减振设计也是一种可行的方法，例如采用调频质量阻尼器(TMD)进行减振控制[16]，利用TMD系统在外界激励下产生的惯性力反作用于结构达到振动控制的目的。由于TMD属被动控制，应根据具体桥梁采取不同控制策略，包括采用单个(STMD)或多个(MTMD)阻尼器，优化设计参数和可能的安装位置以达到所需减振效果等。

6　结论

通过对主跨为100m的人行钢悬索桥进行动力特性数值计算与现场测试可知： (1) 该桥低频范围的结构振动模态较密集，前5阶振型以加劲梁振动为主，结构竖向、横向振动基频均小于1Hz，对行人激励较敏感，容易引起振动病害。 (2) 受构件病害或潜在损伤影响，桥梁实际状态与设计情况有差异，应根据数值计算与现场动力测试结果，综合分析在役人行钢悬索桥的动力特性。 (3) 脉动法所需激振能量小，能稳定识别结构低阶模态参数，可用于人行钢悬索桥动力特性测试。 (4) 人行悬索桥具有较大的跨越能力，加劲梁采用型钢纵横梁后，结构整体刚度不足，设计中应重视基频过小引起的振动问题。在不改变结构原设计参数的前提下，可安装减振装置改善结构动力性能，建议结合技术经济指标与施工条件设计减振方案。