由相关变化率求相关速度

黄 鹏

(重庆巴蜀常春藤学校　重庆　401127)

相关速度就是两个通过某种方式联系起来的速度，它们可以通过媒介(轻绳或轻杆等)、直接接触或不变量相关联，在题目中往往已知一个速度求另一个速度．在运动学中我们把位移对时间的变化率定义为速度，那么求相关速度也可以理解为已知一个变化率求另一个变化率，这正是数学中的相关变化率问题．

下面分别通过3类不同相关速度的几个经典例子探讨由相关变化率求相关速度的方法，试图以对比求解的方式加深大家对相关速度的理解．

1　媒介关联

【例1】如图1所示，某人在岸边用轻绳以速度v0匀速拉动小船使之靠岸，当绳与河夹角为θ时，船的速度为多大？

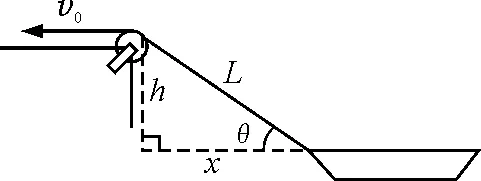
图1　例1题图

运动分解法：因轻绳不可拉伸，故人与小船沿绳方向速度相等．如图2所示，分解船速

v1=v0=vcosθ

则

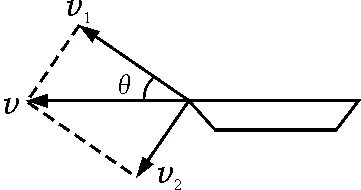
图2　船速度分析

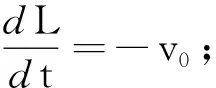
由勾股定理，得

x2+h2=L2

两边对t求导，有

解得

负号表示x减小速度向左．

小结：对轻绳模型求相关速度运动分解法较为简洁，但是在实际学习中，学生很难分辨应该分解绳速还是船速，复习时不妨引入相关变化率法进行一题多解，以帮助学生突破该难点，同时发散学生的思维．

【例2】如图3所示，长20 m的轻杆AB靠在高12 m的墙MN上，接触点M距B端5 m，沿水平方向以5 m/s速度向右拉A端时，B端向下的速度为多大？

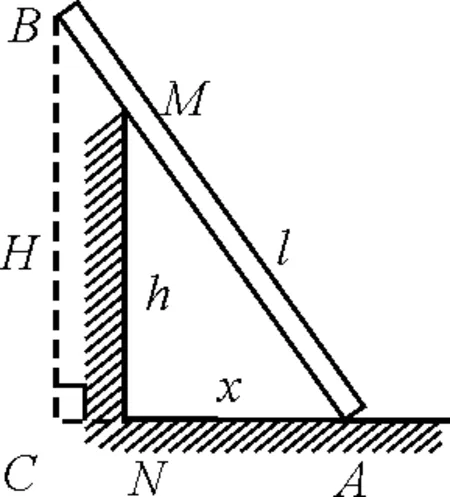
图3　例2题图

运动分解法：因轻杆不可拉伸，故A端与B端沿杆方向速度相等．如图4所示.

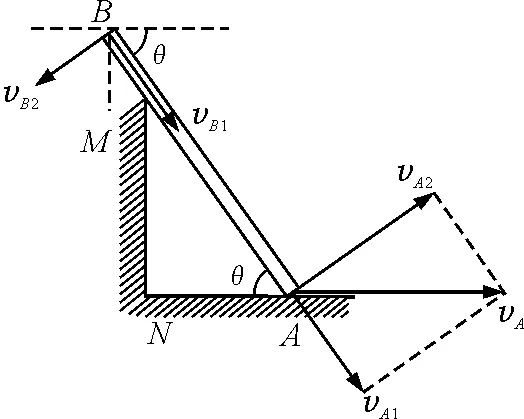
图4　A端速度分解

分解A端的速度

vA1=vB1=vAcosθ

又

则B端沿杆速度vB1=3 m/s．由A端与B端绕M点转动的角速度相等，又

vB2=ωrBM

且

vA2=ωrAM=vAsinθ=4 m/s

则

将vB1和vB2的竖直分量求和得

vBy=vB1sinθ+vB2cosθ=3.2 m/s

相关变化率法：如图3所示，MN=h，AB=L，h和L不变；A端到墙角N的距离为x，其变化率为

AM=l

解得

vBy=-3.2 m/s

负号表示高度减小速度向下．

小结：用运动分解法解此例时，易错判B端速度竖直向下，在求出vB1=3 m/s后，分解B端速度即求出vB=3.75 m/s．其实B端并未受约束，速度并非向下．我们要注意轻杆模型比轻绳模型增加了转动关联的可能性，此时利用两端角速度相等便能得解．而采用相关变化率法不仅可以避开上述陷阱，计算也相对简便．此类模型在2015年高考全国Ⅱ卷第21题中也出现过．

2　接触关联

【例3】如图5所示，半径为R的半圆凸轮以等速v0沿水平面向右运动，带动从动杆AB沿竖直方向上升，O为凸轮圆心，P为其顶点．求：当∠AOP=θ时，AB杆的速度大小．

图5　例3题图

运动分解法：因凸轮和杆不分离，故它们沿接触面法向分速度相等．如图6所示，沿接触面法向和切向分解凸轮和杆的速度得vA1=v1，即vAcosθ=v0sinθ，则vA=v0tanθ．

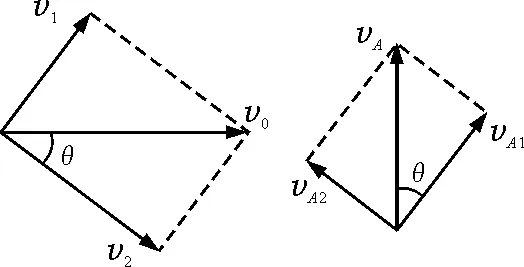
图6　运动速度分解

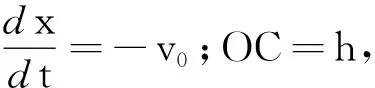
小结：采用相关变化率法可以避免繁琐的速度分解，只要明确已知速度和所求速度分别对应的变化率，列出两变量的关系式求导即可得解．

【例4】距河岸(看成直线)500 m处有一艘静止的船，船上的探照灯以转速n=1 r/min转动．当光束与岸边成60°时，光束沿岸边移动的速率为()

A.52.3 m/sB.69.8 m/s

C.3.14×103m/sD.4.18×103m/s

运动分解法：如图7所示，∠OAB=60°，灯到岸的距离为OB=L，因光束沿岸运动受转动约束，故将沿岸速度分解到切向和法向，则切向分速度为vA1=vAsin60°=ωrOA，又rOAsin60°=L且ω=2πn，解得vA=69.8 m/s．

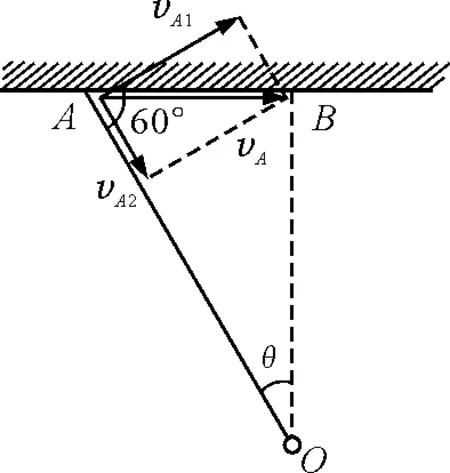
图7　运动速度分解

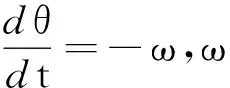
小结：本例为简单的交叉点速度模型，如果能厘清合速度与分速度采用运动分解法将较为快捷；若对求导熟悉采用相关变化率法也很方便．类似模型在2009年清华自招试题中也出现过．

3　流体关联

【例5】一个底面半径为0.1 m的直立圆柱形桶以30 L/min的速率排出液体，桶内液面下降的速率是多少?

解析：排出液体处和桶内液面处液体流量相等，则Q=vπr2=30 L/min，得v=0.96 m/min．

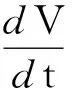
【例6】以1 000 cm3/s的速率把空气冲入气球，当气球半径为8 cm时，半径增大的速率是多少？

解析：冲气处和气体接触球皮处气体流量相等，则Q=v·4πr2=1 000cm3/s，解得v=1.24 cm/s．

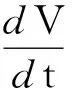
则

小结：对于流体关联模型，若能准确把握流量不变，则可选择直接求解；如果对流量概念理解困难，那么由体积公式求导也不失为一种好的选择．

综上，3类相关速度既有共同遵守的一般规律，又有各自的相关特点所决定的特殊规律．相关变化率法就是一种抓住它们共性的方法，它将复杂问题求解简化为两个步骤：先借助不变量建立起变量与变量之间的关系方程，再在方程两边对t求导数即得相关速度之间的关系，这样让学生对相关速度问题求解有章可循．作为数学知识在物理中的应用，相关变化率法不仅可以开阔学生视野、激发学生兴趣，还能引导学生从数学本质思考相关速度的普遍规律．现在导数属于高考数学二级要求的必考内容，而且近几年已以压轴题的形式出现，所以在中学物理教学中开展相关变化率法教学是可行而必要的．