基于遗传算法的动力总成悬置系统隔振优化
2018-07-13娄小宝陈达亮
娄小宝陈达亮
(1.浙江吉利汽车研究院有限公司;2.中国汽车技术研究中心)
振动解耦和合理匹配固有频率是动力总成悬置系统设计的2个主要问题。从振动解耦角度,为了改善橡胶悬置的隔振效果,文献[1]分析了V型悬置组的力学特性和设计方法,指出如果利用V型悬置组的解耦功能,能够解除动力总成悬置系统的侧倾-横移耦合振动,从而提高悬置系统的隔振性能。由于受到发动机舱的空间限制,V型悬置组在实际工程应用中有时难以实施。为了在有限的空间内获得较好的解决方案,文献[2-4]最早运用数学的优化手段进行悬置系统的设计,以合理配置悬置系统固有频率和自由度之间的振动解耦为目标函数,以悬置刚度和位置参数为设计变量进行优化计算,取得了比较令人满意的优化结果。动力总成悬置系统参数的优化是一个非线性优化问题,目标函数存在非凸性。由于多极值点的存在,使得传统的优化算法容易陷入局部最优。文章运用现代智能优化算法——遗传算法(GA)对悬置参数进行了优化设计,并探讨了不同算法在相同可行域内可搜索范围的大小。

1 动力总成悬置系统动力学模型
由于动力总成悬置系统的固有频率一般在30 H z以下,远比系统作为弹性体的最低阶模态频率(大约60 H z以上)低很多,因此动力总成与悬置所组成的振动系统在分析频段内只存在刚体模态。在这个频段上,可将动力总成视为刚体[5]。为了简化所研究的问题,忽略了车架系统的影响,假设动力总成直接安装在刚性地基上。这样将动力总成悬置系统简化为一个6自由度模型,并在曲轴坐标系oxyz下对动力总成悬置系统动力学特性进行分析[6-7]。该坐标系原点位于动力总成质心处,y轴平行于曲轴中心线指向发动机前端,x轴平行于气缸中心线指向发动机缸盖,z轴按右手定则确定,如图1所示。
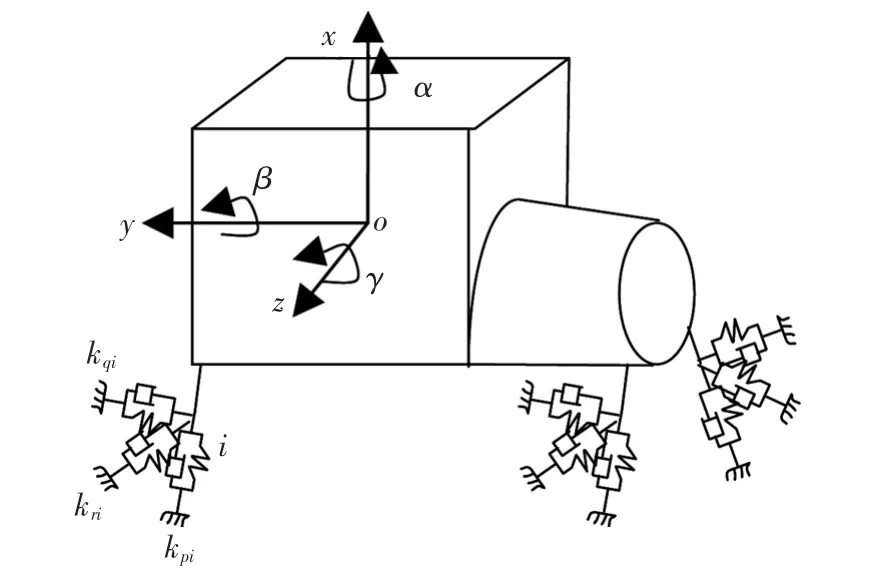
图1 动力总成悬置系统6自由度动力学模型图
在小振幅振动作用下,由于悬置块的阻尼较小,主要作用是降低共振峰值,对系统固有振动特性的影响不大,因此在分析悬置系统自由振动时可以略去不计,则系统的振动微分方程式为:

M,K——系统质量矩阵和刚度矩阵。
由式(1)可求得动力总成悬置系统的各阶模态固有频率和振型矩阵(Φ)。
当采用能量指标判定振动模态的解耦程度,一般用某一自由度方向上的动能占某阶振动模态总动能的百分比作为模态解耦评价指标,在文中称作该方向的解耦度。由系统的M和Φ可求出系统在做各阶主振动时的能量分布矩阵(KE)。当系统以第i阶固有频率振动时,KE中的第k行l列元素为:

式中:Φi——Φ的第i个列向量,即系统的第i阶主振型;
(Φi)k,(Φi)l——Φi的第k及第l个元素;
mkl——KE中第k行l列元素;
ωi——系统第i阶固有频率,H z;
i,k,l=1,2,…,6。
系统以第i阶固有频率振动时第k个广义坐标分配到的能量占系统总能量的百分比为:
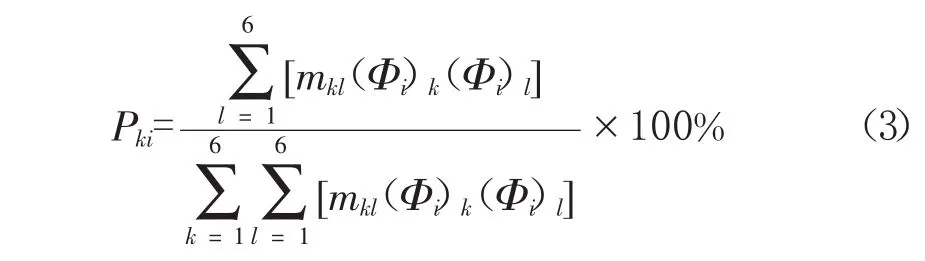
由式(3)可得系统以解耦度为评价指标的振动能量矩阵(KET)。
2 优化数学模型
发动机悬置系统的优化设计通常以悬置的安装位置、倾斜角度及三向主刚度值作为设计变量,可以从不同角度提出目标函数和约束条件来建立不同的优化数学模型。
2.1 目标函数
动力总成悬置系统有多个性能指标,彼此之间存在耦合关系。因此,确定目标函数时必须综合考虑这些指标参数,以使悬置系统具有良好的整体隔振性能。在动力总成的优化设计计算中,目标函数可以是合理配置系统固有频率和自由度振动解耦,低化侧倾模态和侧倾解耦,最小化悬置点响应力和力矩[8],或最小化驾驶座位处垂向加速度值[9]等。以车身敏感点的振动响应值最小为目标函数理论上是最直接且有效的方法,但是需要考虑到车架的弹性,这使得优化问题变得较为复杂。在无法获得足够精度计算模型的情况下,优化后的悬置在实际中往往并不能起到隔振作用。因此,长期以来一直以动力总成悬置系统的固有频率和振动解耦为目标进行优化计算。以悬置系统的固有频率和振动解耦为目标函数,其表达形式如下:
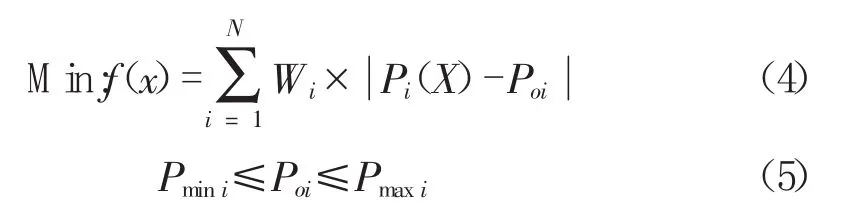
式中:Wi——各项性能指标的权重函数;
X——设计变量;
N——所考虑的子目标函数的数量;
Pi(X)——性能指标函数;
Poi——理想性能指标参数;
Pmaxi,Pmini——第i项性能指标的最大值和最小值。
2.2 设计变量
悬置安装角度和悬置元件的三向主刚度值综合决定了各悬置点的三向刚度(Kxi,Kyi,Kzi),因此,以悬置点的三向刚度值和三向坐标参数作为优化设计的变量,即对于具有n个悬置点的系统,其X的维数为6n。
2.3 约束条件
悬置系统的约束条件主要有系统固有频率(Pfni/H z)约束:
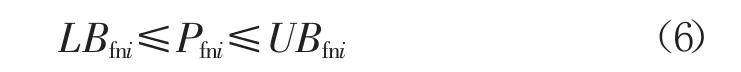
式中:UBfni,LBfni——系统第i阶Pfni的上下限,H z。
动力总成悬置系统在自由度方向振动解耦程度(Pdecoupi)的要求:

式中:UBdecoupi,LBdecoupi——系统在第i个自由度方向上解耦度值的上下限。
还应考虑到悬置系统支承与限位的基本功能和避免动力总成产生过大的位移而与其它部件发生干涉,以及悬置元件的疲劳寿命问题,由这些因素综合对悬置的刚度施加附加约束:
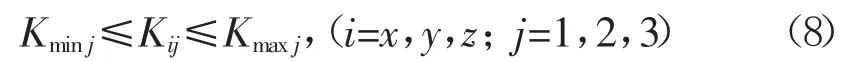
式中:Kij——第j个悬置点的i向刚度,N/m;
Kmaxj,Kminj——Kij可取的最大和最小值,N/m。
另外,受到发动机舱的空间及装配限制,还需考虑各悬置点的位移约束如下:
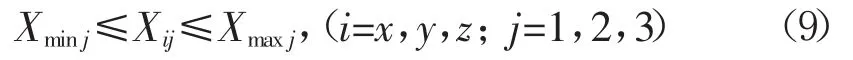
式中:Xij——第j个悬置点的i向位移,m;
Xmaxj,Xminj——Xij可取的最大和最小值,m。
2.4 优化算法
动力总成悬置系统的优化设计属于有约束的非线性优化问题。对于这种优化问题的求解,传统的优化方法可分为2类:一类是直接解法,如坐标轮换法[10-11]、随机方向搜索法、复合形法[12]及序列二次规划法(SQP)等;另一类为间接解法,如拉格朗日乘子法和惩罚函数法[13]等。这些优化算法的共同点就是最优解受到初始点选取的影响,容易陷入局部最优。为此引入GA法对动力总成悬置系统优化设计问题进行研究。
3 实例计算
前轮前驱式轿车发动机悬置系统由于发动机舱空间比较紧凑,因此无法实现对称或V型布置形式,从而给悬置系统的设计带来了困难。为了获得良好的隔振性能,必须对悬置系统进行优化。本例的研究对象为一款紧凑型轿车的发动机悬置系统,该发动机为直列四缸四冲程柴油机,采用三点橡胶悬置布置方式。为便于分析,规定安装于变速器左右侧的悬置分别称为左悬置和后悬置,安装于发动机前端的悬置称为右悬置。动力总成悬置系统的参数,如表1所示。

表1 某轿车发动机悬置系统质量矩阵参数
动力总成的激励源主要是不平衡惯性力和波动转矩激励。在图1所示的坐标系中,二者的作用方向为沿x和β(车身垂直方向)方向。为了使系统获得良好的隔振效果应尽量提高这2个方向的振动解耦程度,同时降低x方向的固有频率。在避免共振的情况下,还应尽量提高β方向的固有频率,因为人体对低频的垂直振动较为敏感。因此,实例以x和β方向的振动解耦度为目标函数,同时约束这2个敏感方向的固有频率,以及将系统的其它频率规定在合理的范围内。
3.1 序列二次规划法(SQP)
SQP法是最常用的传统优化算法。以悬置系统β向和x向的解耦度为目标函数,运用SQP法对上述动力总成悬置系统进行多目标优化计算。为了检验该算法对此问题的适应性,取不同初始值点进行计算比较,以判断所得结果是否为全局最优解。在容许的参数变动范围内,主要计算2种不同初始值点的情况,分别命名为工况1和工况2,具体参数,如表2所示。表3示出运用SQP法优化计算所得的悬置系统的性能参数。

表2 不同工况下发动机悬置系统坐标参数 m
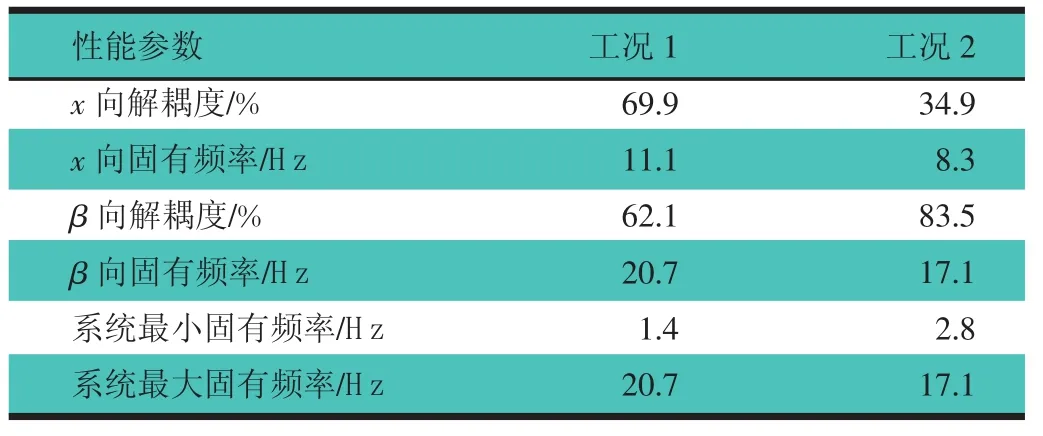
表3 序列二次规划法(SQP)在不同工况下优化计算结果比较
由表3可知:在同样的可行域内,2种工况优化计算结果相差较大。工况1优化计算所得的x向解耦度和β向解耦度比较均衡。相对于工况2而言,工况1的x向固有频率和悬置系统最大频率偏高,但系统最小固有频率值过低,小于2.5 H z,将容易被路面激励激起共振。工况2虽然具有较高的β向解耦度,但是x向解耦程度过低,将不利于悬置系统在汽车高速下隔离由该方向不平衡惯性力所引起的振动。比较2种工况所得的性能参数可知,二者皆不能满足悬置系统设计的要求。一方面说明了SQP法只能获得系统在可行域上的某一局部最优解,优化结果的优劣取决于所选取的计算初始点。因此,采用该法要获得较满意的解,需要依据一定的经验来选取恰当的初始点,或者通过不同初始点计算结果的比较而获得相对最优解,后者将会非常繁琐并且不容易获得全局最优。另一方面,结果也说明了在动力总成悬置系统参数多目标优化设计中存在多极值点的现象,需要应用全局优化方法进行优化计算,才能获得可行域内的全局最优解。
3.2 遗传算法(GA)
GA法作为一种全局优化方法,由于对解空间进行编码操作,因此对于优化目标函数和约束函数的形式没有特别要求,并且优化结果不依赖于初始点的选取,尤其适用于多极值点的优化问题[14-15]。
将GA法应用于上述悬置实例的优化计算,以研究该算法在解决此问题的适应性。为了与SQP法进行比较,分别以x向解耦度、β向解耦度及β向固有频率为单一目标函数,在悬置系统参数设计的可行域内采用SQP法和GA法进行目标函数的最大和最小值范围搜索,结果如表4所示。
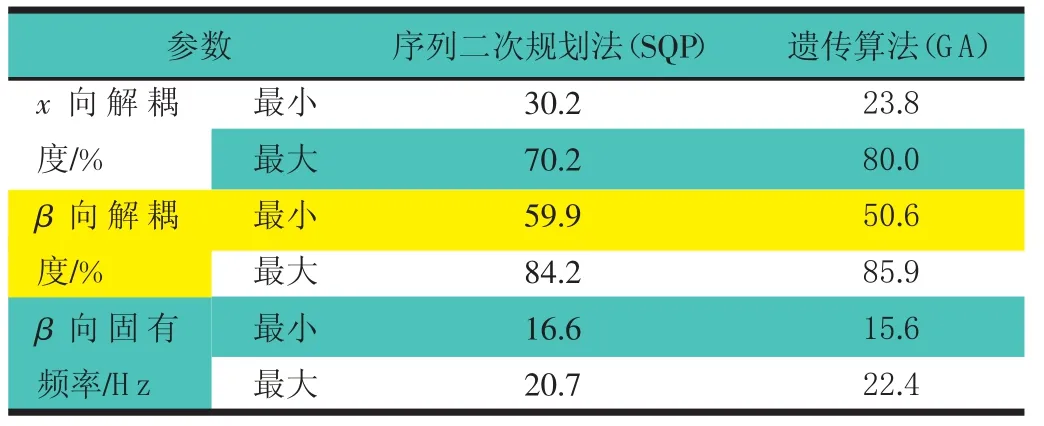
表4 同一可行域上2种算法搜索结果比较
表4说明了2种算法在相同可行域内的搜索能力大小。结果显示在相同的条件下,GA法能够搜索到的x向解耦度范围比SQP法大40%,在搜索β向解耦度时大45%,在搜索β向固有频率时大65%。由此可见,在解决悬置系统多极值点优化设计问题时,GA法将更容易求解到全局最优解。
表5示出GA法在不同初始值点情况下搜索到的最优解所计算得到的系统性能参数值;计算工况,如表2所示。从表5中可以看出,GA法对于优化问题初始值的选取没有特别的要求。这一点对于悬置系统参数的优化设计而言非常重要,因为它使得悬置系统设计的优劣不再依赖于经验,而能够更加方便、快捷地获得满意的结果。

表5 遗传算法(GA)在不同工况下优化计算结果比较
针对所述悬置系统的计算案例,应用GA法和SQP法进行多目标优化计算,获得了设计变量在可行域上的最优解,此时得到的悬置系统各性能参数,如表6所示。

表6 不同算法优化后悬置系统性能参数比较
由表6可知,2种算法获得的悬置系统在β向的解耦度基本相当,但GA法得到的x向的解耦度(60.7%)要远远大于SQP法(34.9%),将有利于提高悬置系统在该方向的隔振性能。另外,在α向和z向的解耦度GA法计算的结果也都大于SQP法。因此,在悬置系统多目标优化设计中,应用GA法进行优化计算更容易获得悬置系统的最优设计方案。
基于GA法的优化结果,计算了优化前后的动力总成悬置系统车架侧振动响应,如图2和图3所示。从图2和图3可以看出,悬置系统起到了更好的隔振作用。
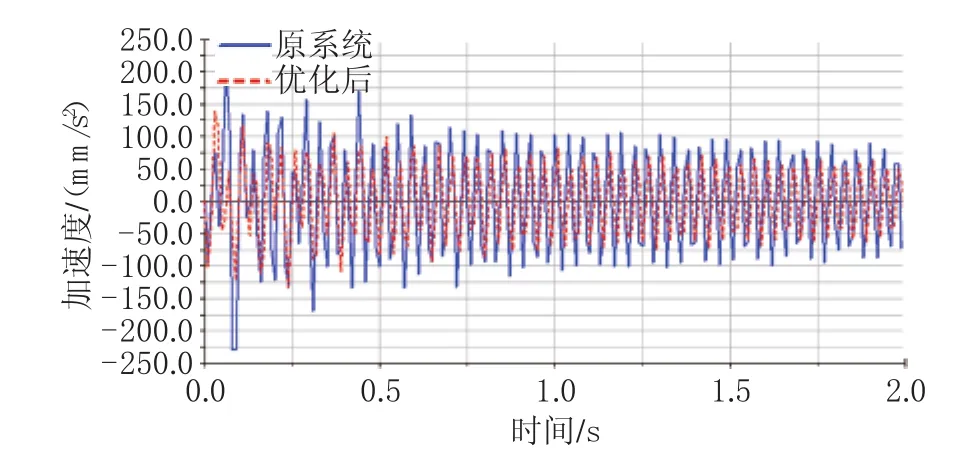
图2 怠速工况下车架侧振动加速度时域响应
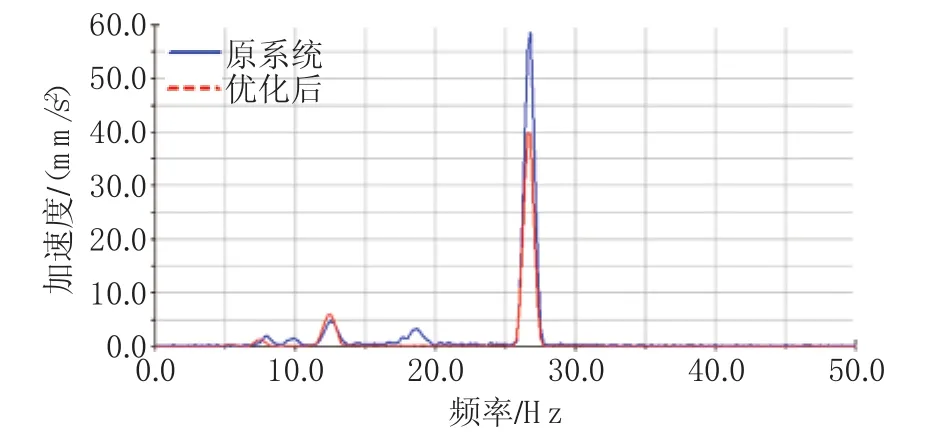
图3 怠速工况下车架侧振动加速度幅频响应
4 结论
动力总成悬置系统参数的优化设计是一个多目标非凸性优化问题,问题本身存在多极值点现象。SQP法优化的结果由于受到初始点选取的影响,容易陷入局部最优,这给悬置系统的设计带来了不确定性,尤其在概念设计阶段,难以获得设计可行范围内的全局最优解。而GA法能够有效地解决悬置系统参数优化设计
中出现的多极值点问题,在设计变量的可行域内更容易搜索到全局最优解。另外,GA法不依赖于初始值的特性,使得动力总成悬置系统优化设计的效率和可靠性大大提高,这对于无法设定初始点的悬置系统概念设计阶段而言,显得尤为重要。
在动力总成悬置系统的优化设计中,上述GA算法同样适用于四点支承的悬置布置形式以及包含动力总成、副车架及车身的多刚体系统的优化。
综合可见,GA法相较于SQP法更加适合于动力总成悬置系统参数的优化设计。
