高中与初中数学函数概念教学的衔接研究

黄清

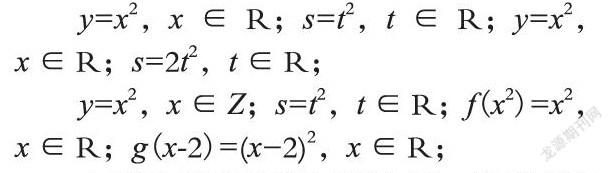
【摘要】在中学数学之中，函数属于核心内容，其一直贯穿在中学数学科目教学之中。而且，数学方法及思想辐射到几何、数列、极限、不等式、方程以及代数等领域，其是对学生辩证观念以及逻辑思维加以培养的良好素材。一直以来，函数部分就是中学教学中的重点和难点，同时也是高考考查的热点内容。近几年来，高考试题当中的几道压轴题多以函数这种形式出现，对导数运用以及和不等式进行结合考查。这都说明函数在数学之中的重要地位。而数学教师怎样才能把初中数学及高中数学中的函数概念有关教学加以有效衔接，是数学教师重点思考及探索的一个问题。

【关键词】高中函数；初中函数；衔接教学

如今，不少高中时期的数学教师并未对初中和高中教学具体衔接这一工作加以重视，致使教学出现了不少问题。还有一些教师即使对衔接教学加以重视，但是也没有抓住衔接工作当中的要点。而本次研究则主要对如何做好衔接工作，进而给课堂教学提供一些可行性的建议。

一、运用类比推理，做好函数衔接铺垫工作

不少高中时期的数学教师实施教学之时，对初中及高中教学中的衔接工作并未加以重视。这些教师觉得，教学任务较重，没有过多时间落实衔接工作，其只需要对教学任务加以完成即可。尽管高中教师普遍教学任务较重，然而教师没有对教学衔接这一工作加以落实难以使得教学效率得以提升。

例如，教师讲授函数概念之时，假设其直接把函数概念告知学生，则不少学生都难以对函数概念加以快速了解，其只能将概念强行记下。因为学生并未对函数概念加以真正理解，所以在对函数概念加以应用之时，就会出现不少问题。在高中生认为自身无法对新知识加以理解以及应用之时，就会逐渐产生一种对函数的畏惧心理。事实上，初中时期，学生就已经对函数知识进行过学习，但初中函数和高中函数存在较大不同。而且，初中函数比较特殊，其概念以及性质比较模糊。而高中生则需要站在更加科学以及更加抽象的角度对函数知识加以理解。虽然学生对于初中及高中函数具体了解存在差异，但二者所讨论以及研究的却是同一问题。如果教师能够把衔接工作做好，就能够让学生对这种异同加以理解，进而让学生迅速对新知识加以理解。

例如，在高中时期，数学教师可让学生对以下函数加以观看及分析：

y=kx，y=kx+b，以及y=ax2+bx+c。

数学教师需让学生对上面三个函数对应的图像加以绘制，并且说出函数图像当中包含的规律以及规律具体应用范围。高中生通过对初中所学知识加以回忆，可以对教师所提问题加以回答。即便一些学生现有知识体系还不健全，经过这一阶段，其也能对对现有知识结构加以补充。当高中生对初中时期函数概念完全理解之后，数学教师需让学生在此进行思考，如：如何通过结合知识来对上面数学概念加以描述？教师可以引导学生听过由此及彼以及对应转换这种思想来对问题加以思考，而这就是类比推理这种思维。当高中生借助这种方法将旧知识变成新知识，就可对新知识进行快速理解。

数学教师将初中函数和高中时期的函数教学有关衔接工作做好，需要引导学生对类比推理这种方法来对新知识加以理解，这样不仅不会造成教学时间的浪费，同时还能使得教学效率得以提高。

二、渗透数学思想，对衔接重点加以把握

高中生在对类比推理这种思想加以应用之后，尽管不少学生会对当前学习目标加以了解，然而学生依然无法抓住学习重点。教师需对学生现有思维水平加以培养，让其对高中数学当中的重点知识加以了解。

例如，在对函数概念加以讲解之时，当学生了解到初中及高中函数所研究内容基本一致，然而研究深度不同之时，就会思考：高中时期的函数本质是什么？要对哪些知识加以学习才能对当前函数知识加以理解？此时，教师可用以下问题来对高中函数有关知识加以理解。

y=x2，x∈R；s=t2，t∈R；y=x2，x∈R；s=2t2，t∈R；

y=x2，x∈Z；s=t2，t∈R；f（x2）=x2，x∈R；g（x-2）=（x-2）2，x∈R；

在学生学完这道习题之后，数学教师可让学生进行相应思考：该题用什么思想来对函数概念加以讨论？通过思考，高中生可发现，在高中数学之中，之所以将集合知识和函数知识加以结合，就是为用更加精确、更加抽象的方法来对函数问题加以讨论。学生以后在对高中函数有关问题加以理解之时，需要从该角度来对问题加以思考。

数学教师将初中及高中的函数概念具体衔接工作做好，能够引导学生借助高中时期所学数学思想对数学问题加以探讨，进而让其对函数本质加以掌握。

三、对知识加以整合，構建完整体系

高中教师在实施函数教学之时，可先让学生对初中时期所学函数概念加以回忆，之后让其将旧知识和新知识加以对应，此时学生便会发现以下对应关系：第一，在初中时期，仅需学生对函数图像基本含义加以了解，而高中则需学生站在抽象角度来对函数的单调性加以理解。第二，在初中，仅需学生对函数存在取值范围以及对应函数值加以理解，但高中则需学生借助单调性这一思想来对函数当中极值问题加以讨论。第三，初中教学仅需学生对特殊并且简单的函数性质加以了解，但高中则需学生借助函数思想来对复杂函数加以讨论。因此，教师需帮学生对现有知识体系加以重新整合，进而让其对函数知识进行深层理解，进而形成完整知识系统。

四、结语

综上可知，高中时期的数学教师需对初中及高中教学整体衔接工作加以重视，帮助学生对知识衔接当中的要点加以把握，让学生逐渐形成健全的知识系统。因此，在课堂上，数学教师需对类比推理加以运用，做好函数衔接铺垫工作，提高数学思想，对衔接重点加以把握，同时对知识体系加以整合，构建完整系统，进而做好数学教学方面的衔接工作。

参考文献：

[1]张苗苗.职高数学与初中数学课程衔接研究——以函数概念对比教学为例[J].中学生数理化（教与学），2018（03）：78-79.

[2]郑文晶.HPM视角下初中、高中、大学教科书函数定义的初探[J].呼伦贝尔学院学报，2017，25（05）：132-135+138.

[3]申奋生.改进高中数学教学措施 做好初高中之间知识衔接[J].学周刊，2015（24）：138.