罗氏沼虾的形态性状对体重的相关性分析
2018-07-12孙海峰刘国兴蒋连玉
孙海峰,刘国兴,蒋连玉
(江苏省淡水水产研究所,江苏 南京 210017)
罗氏沼虾(Macrobrachium rosenbergii),又称马来西亚大虾,隶属于节肢动物门,十足目,长臂虾科,沼虾属,是世界上最大的淡水虾;它盛产于印度-西太平洋地区,具有生长快、易驯养、适应性强、食性广、抗病能力强、生长周期短和高蛋白等特性,是一种养殖量较大的重要经济物种[1-2]。自1976年引种以来,罗氏沼虾已在我国十多个省市自治区进行养殖,但是经过40多年养殖,出现了生长缓慢、蜕壳周期延长或不蜕壳、性成熟提前、抗病力低等种质衰退现象[3-4]。通过人工选育,培育出生长快,抗病力强的良种是当前面临的迫切任务。在选育的过程中,体重和外部形态性状是重要的目标性状,且外部形态性状具有可度量性和直观性,将体重和外部形态性状列为选择指标,将显著提高选育效率[5]。
邓平平等分析了5月龄罗氏沼虾体长、全长等指标对体重的影响,并建立了各形态指标对体重的多元回归方程[6]。耿绪云等分析了中华绒螯蟹幼蟹和成蟹阶段外部形态性状对体重的影响[7]。刘小林等采用相关性分析和通径分析方法对6月龄凡纳滨对虾进行研究,定量地分析了形态性状对体重的影响效果[8]。一般情况下,成体雄性罗氏沼虾比成体雌性罗氏沼虾要大,雄虾第二步足特别发达粗壮,雄、雌间存在差异[9]。尚未在虾、蟹等甲壳动物的研究中发现有对雄、雌进行分别研究的。因此,研究雄、雌各现状间的相互关系,对选育具有实际意义。
本研究运用了相关性分析,逐步回归分析和通径分析对变量间的共线性问题进行分析处理,探讨了扬州市高邮地区4月龄雄、雌罗氏沼虾的主要形态性状,建立体重的多元线性最优回归方程,并分析了保留性状对体重的直接影响和间接影响,为罗氏沼虾的选育以及更深层次的研究提供理想的测量指标。
1 材料与方法
1.1 试验材料
在扬州市高邮养殖塘口采集4月龄罗氏沼虾样本,样本采集后将其置于适宜温度的水箱中,利用增氧泵持续增氧,采集的样本运回实验室后进行筛选,对于新蜕皮的软体虾和虾体各部位不全的虾体舍弃不用,挑选200只供实验用,雄、雌各半。
1.2 形态性状与重量性状的测量
去除罗氏沼虾体表水分后,使用电子天平测量罗氏沼虾的活体重(Y),测量精度为 0.0001 g;用电子游标卡尺测量体长(X1)、腹尾长(X2)、螯长(X3)、第一腹节宽度(X4)4个参数,测量精度为 0.01 mm,以下是对以上4项参数的一个简要说明[10],体长:从额剑前端至尾节末端;腹尾长:头胸甲末端至尾末端;螯长:大螯基部至大螯末端;第一腹节宽度:头胸甲后第一腹节的宽度。
1.3 数据分析方法
采用SPSS 17.0软件对各现状指标数据进行综合整理和计算处理,得到各性状均值、标准差和计算出变异系数。本实验N=100,属于大样本,正态性检验时采用Kolmogorov-smirnov Test检验。对所测各性状进行相关分析、表型性状对体重性状的通径分析,计算决策系数。采用多元逐步线性回归法剔除偏回归系数中不显著性状,以体重为因变量,以其他指标为自变量,建立表型性状与体重性状的多元回归方程。
2 结果与分析
2.1 形态学参数统计
所测体重和形态性状的数据资料经初步整理后的表型统计量见表1。由表1可知,雄性罗氏沼虾各性状变异系数由大到小的顺序为:体重>螯长>腹尾长>第一腹节宽度>体长,体重的变异系数最大(21.39),在形态性状中螯长的变异系数最大(18.21);雌性罗氏沼虾各性状变异系数由大到小的顺序为:体重>螯长>第一腹节宽度>腹尾长>体长,体重的变异系数最大(20.91),在形态性状中螯长的变异系数最大(13.94)。
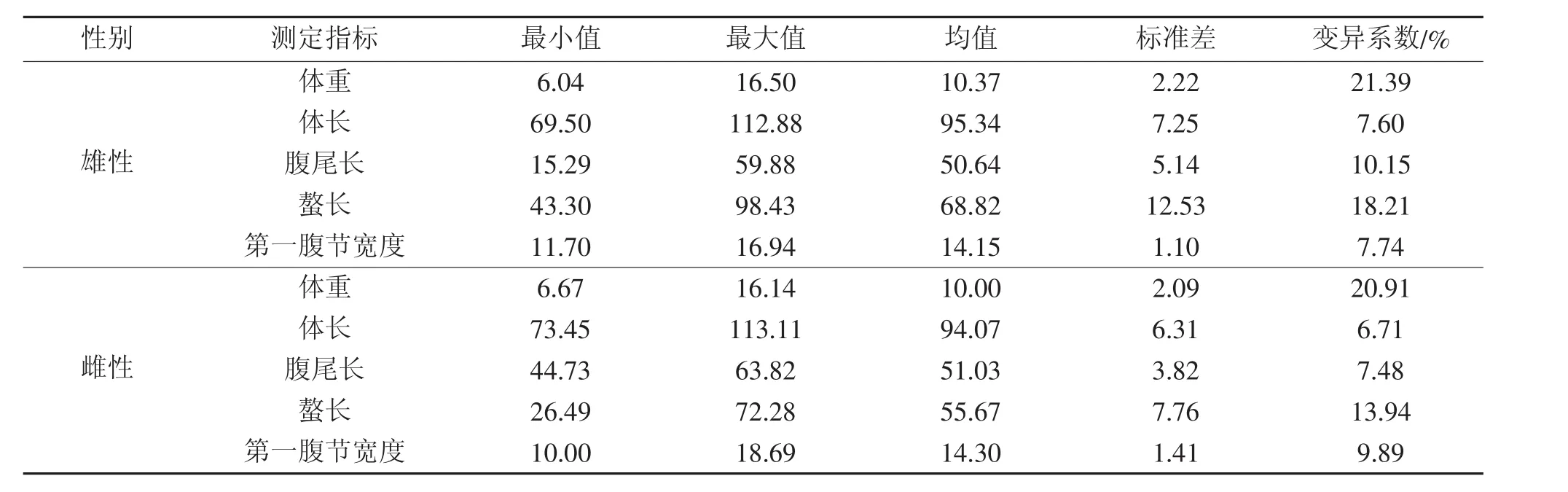
表1 所测各性状的表型统计量(n=100)
2.2 形状间的相关分析
由表2可知,实验所测定雄、雌体重、体长、腹尾长、螯长和第一腹节宽度各性状间相关关系均极具统计学意义(P<0.01),雄性各形态性状对体重的相关系数大小依次为:体长>第一腹节宽度>螯长>腹尾长,雌性各形态性状对体重的相关系数大小依次为:体长>腹尾长>第一腹节宽度>螯长,表明将所选的指标用来进行相关性分析具有很重要的实际意义。

表2 罗氏沼虾各性状间表型相关系数
2.3 数据正态性检验
在进行通径分析和多元回归分析之前需对因变量进行正态分布检验,只有当变量为正态变量或近似正态变量时,之后的分析才具有统计学意义。由于本实验样本数n=100,可以采用K-S test方法对自变量和因变量进行正态性检验,正态分布检验的结果见表3,显著水平均大于0.05,所以雄、雌罗氏沼虾五个测定指标均符合正态分布,即可以对体重进行回归分析。

表3 正态性检验结果
2.4 建立逐步回归方程
表4可以看出随着自变量被逐步引入回归方程,回归方程的复相关系数R和决定系数R2在逐渐增大,说明引入的自变量对体质量的作用在增加。其中雄虾分析中,相比于模型1和2,模型3的R2=0.634最大,则剩余因子较小,模型3对体重的作用有影响的自变量考虑最全面,与数据的拟合度最好;雌性的分析中,相比于模型1和2,模型3的R2=0.595最大,则剩余因子较小,模型3对体重的作用有影响的自变量考虑最全面,与数据的拟合度最好。由表5方差分析可知,P<0.01,说明雄、雌罗氏沼虾体重在个体间有差异性。表6可以看出回归分析中每一步排除的变量。根据表7,雄性的体长、螯长和第一腹节宽度,雌性的体长、腹尾长和螯长显著性检验结果均小于0.05,自变量与因变量之间差异有统计学意义,都应留在方程中。雄性体重与各因子的线性回归方程为:Y=-13.950+0.123X1+0.049X3+0.647X4;雌性体重与各因子 的 线 性 回 归 方 程 为 :Y=-15.735+0.193X1+0.205X2-0.052X3。

表4 模型概述
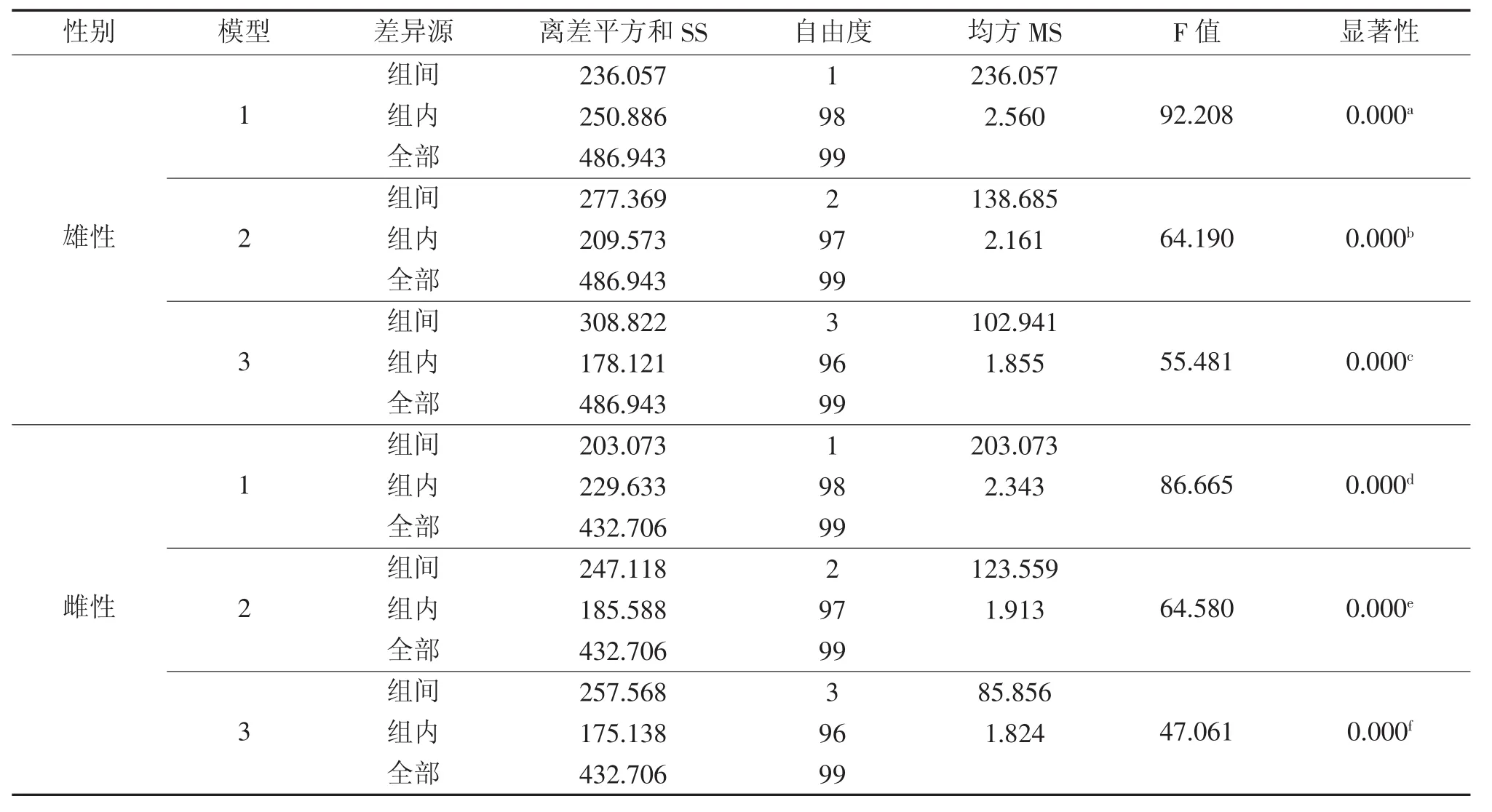
表5 体重方差分析

表6 已排除的变量

表7 偏回归系数和回归系数的显著性检验
2.5 计算间接通径系数
从表2的Pearson Correlation输出结果可得到自变量与因变量之间的相关系数。在雄性中,体长(X1)、螯长(X3)与第一腹节宽度(X4)的相关系数分别为:r13=r31=0.363,r14=r41=0.599,r34=r43=0.309。由表7可知,通径系数(直接作用)分别为:P1y=0.404,P3y=0.279,P4y=0.320。由通径分析的理论可知,r1y=P1y+r31×P3y+r41×P4y=0.696,r3y=P3y+r13×P1y+r43×P4y=0.524,r4y=P4y+r14×P1y+r34×P3y=0.648(结果与表 2 一致)。X1通过 X3对 Y 的间接通径系数为:r31×P3y=0.101,X1通过 X4对 Y 的间接通径系数为:r41×P4y=0.192。X3通过 X1对 Y 的间接通径系数为:r13×P1y=0.147,X3通过X4对 Y 的间接通径系数为:r43×P4y=0.099。X4通过X1对 Y 的间接通径系数为:r14×P1y=0.242,X4通过 X3对 Y 的间接通径系数为:r34×P3y=0.086。
在雌性中,体长(X1)、腹尾长(X2)与螯长(X3)的相关系数分别为:r12=r21=0.574,r13=r31=0.586,r23=r32=0.282。由表6可知,通径系数(直接作用)分别为:P1y=0.583,P2y=0.374,P3y=-0.192。X1通过 X2对 Y 的间接通径系数为:r21×P2y=0.215,X1通过 X3对 Y 的间接通径系数为:r31×P3y=-0.113。X2通过 X1对 Y 的间接通径系数为:r12×P1y=0.335,X2通过 X3对 Y 的间接通径系数为:r32×P3y=-0.054。X3通过 X1对 Y 的间接通径系数为:r13×P1y=0.342,X3通过 X2对 Y 的间接通径系数为:r23×P2y=0.105。
2.6 决策系数
决策系数是通径分析中的决策指标,其可将自变量对响应变量的综合作用进行排序,确定主要决策变量和主要限制变量。决策系数的计算公式:R2(i)=2Pi×riy-Pi2,其中 R2(i)是自变量 i的决策系数;Pi为自变量的直接通径系数;riy为自变量i与响应变量y的相关系数。R2(i)>0,表明自变量对于响应变量起增进作用,R2(i)<0,表明自变量对于响应变量起抑制作用[11]。
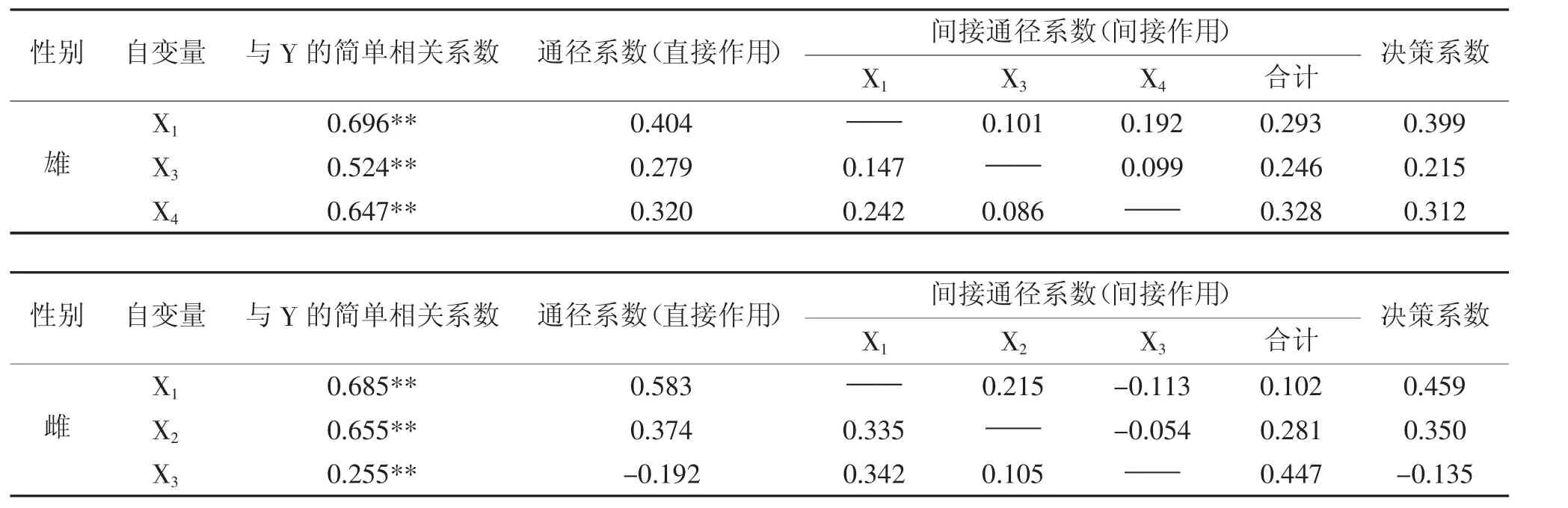
表8 雄、雌罗氏沼虾3个形态性状对体重的影响
由表8可知,在雄性罗氏沼虾中,按决策系数排序为:R2(1)> R2(4)> R2(3)>0,故 X1为主要决策变量(直接决定作用最大),X1、X3与X4均对y起增进作用。在雌性中,按决策系数排序为:R2(1)>R2(2)>R2(3),且R2(3)<0,故X1为主要决策变量(直接决定作用最大),X3为主要限制变量(直接作用最小)。
3 讨论
3.1 自变量的确定
通径分析克服了相关性分析与多元回归分析的不足,即相关性分析不能全面考察变量间的相互关系,结果有一定的片面性;多元回归分析在一定程度上能够消除变量之间的混淆,但由于偏回归系数带有单位,不能直接比较原因对结果的效应。而通径系数是标准化的偏回归系数,表示自变量对因变量直接作用的大小,从而使原因对结果的效应能直接进行比较,包含了两者的直接作用和通过其他变量的间接作用。通径系数随着所选自变量个数和性质的不同而发生改变,考虑的形状越多,结果越可靠,但统计分析也就越复杂,不能突出重点[7-8]。同时,通径系数也是回归方程标准化变量的偏回归系数,因此逐步回归分析获得的最优回归方程自变量与通径分析保留的自变量一致。
罗氏沼虾个体的生长是由于不断蜕壳而逐渐增长的,个体大小通过外部形态性状如:体长、螯长、腹尾长、第一腹节宽度等指标来描述,在本研究中,雄性个体间相关性分析、通径分析达到显著水平的体长、螯长和第一腹节宽度作为测量指标;雌性个体间的相关性分析、通径分析达到显著水平的体长、腹尾长和螯长作为测量指标。
3.2 影响罗氏沼虾体重的主要性状的确定
罗氏沼虾的生长表现为外部形态和体重等数量性状的增长,二者存在不同程度的相关性。由于罗氏沼虾在4月龄时雌、雄个体间表现出性别差异性,因此,本研究将样本分为雄、雌两组进行分析,以4个外部形态性状为自变量(X),体重性状为依变量(Y),分别进行相关分析、多元线性回归分析和通径分析。
由表8可知,雄性罗氏沼虾中3个自变量对体重的直接影响中,体长X1的直接作用最大,第一腹节宽度X4次之,螯长X3最小。体长X1通过螯长X3和第一腹节宽度X4对体重Y的间接作用小,说明对体重Y影响较大的自变量是体长X1。第一腹节宽度X4通过体长X1对体重Y的间接作用最大,其间接通径系数 r14×P1y=0.242。至于螯长 X3,其直接通径系数和间接通径系数均较小,对体重Y的影响不大。从决策系数来看[11],体长的决定作用最大,第一腹节宽度次之,螯长的决定作用最小。决策系数结果与相关系数和直接通径系数结果一致,说明体长是影响雄性罗氏沼虾体重的重要自变量,其次是第一腹节宽度。
雌性罗氏沼虾中3个自变量对体重的直接影响中,体长X1的直接作用最大,腹尾长X2次之,螯长X3最小。体长X1通过腹尾长X2和螯长X3对体重Y的间接作用小,说明对体重Y影响较大的自变量是体长X1。螯长X3通过体长X1对体重Y的间接作用最大,其间接通径系数r13×P1y=0.342,但螯长的直接通径系数为-0.192,说明螯长对体重作用小。从决策系数来看,体长的决定作用最大,腹尾长次之,螯长的决定作用最小。决策系数结果与相关系数和直接通径系数结果一致,说明体长是影响雄性罗氏沼虾体重的重要自变量,其次是腹尾长。
罗氏沼虾的在饥饿的情况下会出现同类相残打斗,弱者或者蜕皮后软壳虾常成为其同类的饵料[9]。罗氏沼虾喜欢打斗,霸占地盘,争斗行为中毁损伤肢体和螯肢,且个体大的虾之间的争斗行为更为凶狠,受过损伤的螯肢生长会较正常的螯肢短些[12]。从雌、雄分析的相关系数来看,自变量螯长与因变量体重之间的相关性最小,从直接通径系数和决策系数来看,螯长对体重的直接作用效果较小,很可能是在挑选样本的时很难将受过不同打斗损伤的个体进行剔除,但这也属于正常的误差范围内。
3.3 罗氏沼虾外部形态性状与体重的数量关系
通过相关分析、通径分析和多元回归分析找出影响罗氏沼虾体重的主要表型性状,根据罗氏沼虾生长的特点,以罗氏沼虾体重为因变量(Y),外部形态性状为自变量(X),分别对4月龄雄、雌罗氏沼虾测定资料进行多元线性回归分析,逐步删除偏回归系数不显著的性状,建立雄、雌罗氏沼虾最优多元线性回归方程,描述了罗氏沼虾主要形态性状与体重性状间的数量关系。最优多元线性回归方程所保留的自变量与通径分析结果一致,且各自变量对体重的偏回归系数均达到显著水平(P<0.05)或极显著水平(P<0.01),确保最优多元线性回归方程具有实际意义,分别为4月龄雄、雌罗氏沼虾的生长提供了多元线性回归方程,为其选择育种提供了理论依据和理想的测度指标,可用于指导下一步罗氏沼虾的实验研究工作。
4 结论
本文对罗氏沼虾的体重、体长、腹尾长、螯长和第一腹节宽度5个形态性状进行测定,采用相关分析、多元回归分析和通径分析等方法计算各性状之间的相关系数,建立了理想的最优回归方程。
