支付模糊图合作博弈分配模型及其应用

苏东风, 杨 洁

(1.福州大学经济与管理学院, 福建 福州　350116; 2.福建农林大学管理学院, 福建 福州　350002)

0　引言

博弈论也称对策论, 合作博弈作为博弈论的重要分支, 主要研究局中人如何形成联盟以及联盟收益(支付)如何分配.传统合作博弈中, 用实数表示联盟收益的期望值, 即合作博弈的支付函数是清晰的.然而通常情况下, 合作博弈的联盟收益是局中人在真正结盟之前对联盟获利的一种预判估值, 其受到现实环境不确定性、 信息不准确性, 以及局中人主观期望与风险态度差异等因素影响, 联盟收益估值几乎都为模糊值[1-2].如, 常见联盟收益往往因市场需求、 市场交易价格等不确定只能模糊估值, 往往有“销售量在18万件左右”, “总收益大约是450万元”等表述.为此, 应用模糊数表示联盟期望收益, 即合作博弈的支付函数是模糊的, 可以提升决策的科学性.支付模糊合作博弈问题自Mares[2]提出以来, 不断受到相关学者的关注[3-4], 特别是模糊支付合作博弈的Shapley值最为典型[5-7].但此类合作博弈研究大都集中于“局中人可自由结盟”假设, 其模糊解未体现出结盟的限制性.现实生活中, 由于局中人之间受到资源、 文化冲突或竞争地位等因素的影响, 其合作结盟往往不是任意的, 而是具有某种限制约束性.

针对此类情况, Myerson[8]用无向连通图表示效用可以转移的合作博弈, 以图的顶点表示局中人, 以图的边表示局中人的交流联系, 从而引入了具有交流结构的合作博弈(也称“图合作博弈”), 并提出著名的Myerson值.沿此思路, 部分学者开展了一类限制交流合作博弈的经典A-T解研究.2008 年, Talman等[9]定义了无圈图合作博弈的平均树解(average tree solution , 简称为“A-T 解”)和子核心, 并讨论A-T 解可能存在于子核心中的条件.Herings等[10]讨论了A-T 解的分支有效性和分支公平性两个特殊性质.Mishra等[11]、 Béal等[12]深入论证了该解具有的优良性质, 如在超可加合作博弈中A-T解存在于核心中, 但Myerson值却不满足； A-T 解边际特征向量的计算量大大简化等.具有限制交流结构图合作博弈的研究虽然能体现“限制结盟”的特点, 但研究主要集中于清晰确定信息的经典研究之中.当前, 仅少量图合作博弈文献涉及模糊信息.Jiménez-Losada等[13]定义了具有模糊交流结构合作博弈的模糊Myerson值.聂翠平等[14]定义了联盟模糊的图合作博弈, 并对经典A-T 解进行推广.文[15]则针对区间值模糊联盟拓展了模糊A-T解.可见, 目前关于模糊信息下图合作博弈的研究远远少于任意结盟假设下的模糊合作博弈研究.

鉴于现实合作结盟中约束性和模糊性的普遍存在, 本研究针对具有限制交流结构的图合作博弈, 通过引入λ截集置信水平, 提出一种具有支付模糊的图合作博弈分配解模型, 建立公理化体系对此解的性质进行讨论.此外, 将模型应用到产学研协同创新收益分配实例中, 并与模糊Shapley值进行比较分析.

1　模糊数及其λ截集

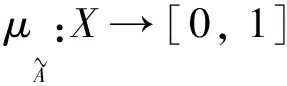
(1)

模糊数是实数的推广, 而区间数是十分重要的一种模糊数.区间数不仅具有集合的特征, 而且具有实数的某些性质.区间数有如下运算规则：

2　具有限制结盟的模糊图合作博弈及其A-T解

2.1　具有限制结盟的模糊图合作博弈

三元组(N,v,L)表示经典(清晰)图合作博弈, 其中:N={1, 2, …,n}为有限局中人集合;v:2N→R为支付函数;L⊆{{i,j}|i≠j,i,j∈N}为边集, 表示局中人交流的集合, 在交流结构中只有连通的节点才可能结成联盟.若L={{i,j}|i≠j,i,j∈N}, 称(N,v,L)为具有完全交流结构的合作博弈, 即各局中人可自由结盟.通常所说的合作博弈便指的是这一类.若L⊂{{i,j}|i≠j,i,j∈N}, 则(N,v,L)为具有限制交流结构的合作博弈, 即局中人不能自由结盟.此外, 不含任何圈的合作博弈称为无圈合作博弈.本研究讨论此类无圈且有限制交流结构的图合作博弈.

经典交流结构合作博弈中,n维A-T解AT(N,v,L)定义为[9]：

(2)

其中：i=1, 2, …,n, |BL|为BL的元素个数.

针对联盟收益的模糊性或者不确定性, 利用模糊数来表示不确定支付函数值, 引入具有支付模糊的图合作博弈.

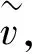
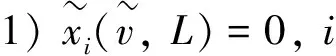
2.2　模糊图合作博弈的A-T解及其性质

(3)

(4)

根据定理1和区间模糊数相关运算规则, 有：

(5)

(6)

同理, 可得：

(7)

证明对于任意i∈N,λ∈[0, 1]和B∈BL, 有：

由式(7), 有：

因此,

从而：

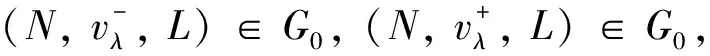
(8)

进而, 根据式(5)和式(7), 有：

同理, 根据式(6)和式(8), 有：

因此, 可得：

从而：

根据式(3), 可知：

3　产学研协同创新收益分配应用

3.1　合作结盟及其收益分配

假设最大联盟{1, 2, 3} 形成, 根据式(1)可得不同置信水平λ下的局中人的收益值, 如表1所示.

表1不同置信水平λ下的协同创新联盟收益

Tab.1Payoffsofcollaborativeinnovationalliancesunderdifferentconfidencelevelsλ(万元)

Lv λ({1})v λ({2})v λ({3})v λ({1, 2})v λ({2, 3})v λ({1, 2, 3}) 1.02.05.04.014.018.033.00.9[1.9, 2.1][4.8, 5.2][3.8, 4.1][13.6, 14.4][17.7, 18.4][32.2, 33.7]0.7 [1.7, 2.3][4.4, 5.6][3.4, 4.3][12.8, 15.2][17.1, 19.2][30.6, 35.1]0.5 [1.5, 2.5][4.0, 6.0][3.0, 4.5][12.0, 16.0][16.5, 20.0][29.0, 36.5]0.3 [1.3, 2.7][3.6, 6.4][2.6, 4.7][11.2, 16.8][15.9, 20.8][27.4, 37.9]0.1 [1.1, 2.9][3.2, 6.8][2.2, 4.9][10.4, 17.6][15.3, 21.6][25.8, 39.3]0 [1.0, 3.0][3.0, 7.0][2.0, 5.0][10.0, 18.0][15.0, 22.0][25.0, 40.0]

根据式(4)和式(5)可求出不同置信水平λ下联盟{1, 2, 3}协同创新分配收益策略, 各局中人具体分配收益值如表2所示.

表2　不同置信水平λ下的协同创新分配收益策略

类似地, 可求出不同协同创新联盟组合下的分配收益策略.

3.2　结果与方法对比

可见, 在此支付模糊下的协作创新收益分配策略是可行的, 如当置信水平λ=0.5时, 高校可分配得到收益为4.00～8.33万元, 企业可分配得到收益为14.50～21.17万元, 科研机构可分配得到收益为6.33～11.17万元.此外, 随着置信水平λ的取值越大, 收益分配的区间范围越小.

当前, 合作博弈的Shapley值方法是应用最普遍的方法, 但该解是基于可任意结盟假设, 求解过程需要得知所有子联盟收益值.针对此类情况, 有学者认为若局中人之间无合作, 其联盟收益便是单干收益之和, 即v({1, 3})=v({1})+v({3}), 进而利用Shapley值进行收益分配.本研究中, 若置信水平λ=1, 基于Shapley值的各局中人具体收益分配为：φ1(v1)=7.5万元,φ2(v1)=15.0万元,φ3(v1)=10.5万元.对比结果, AT1(v1,L)<φ1(v1), AT2(v1,L)>φ2(v1), AT3(v1,L)<φ3(v1).可知, A-T解法相比较于Shapley值法, 企业分配收益有所增加, 而高效和科研机构分配收益有所减少, 这源于企业的无可替代地位.此结论从理论角度解释为在社会创新活动中, 收益最大的往往是企业类组织.由此可见, 局中人在联盟中的获利能力不仅取决于它对联盟收益的边际贡献, 还取决于在联盟中所处的地位, 地位越重要越稀缺其所得分配则越多.

4　结语

联盟组建及其合作行为均基于对未来获利情况的预判, 因此预期支付估值由模糊数替代精确值更为合理可信.本研究针对合作具有结盟限制情形, 通过引入λ截集置信水平研究支付模糊的图合作博弈, 并给出相应的模糊A-T解分配模型, 能有效刻画现实结盟情境中的约束性和模糊性.但由于区间数运算规则, 模糊解的区间范围被不断扩大, 不满足类似于经典解的有效性公理.针对这一问题, 定义相对有效性的概念, 并证明模糊解满足相对有效性公理.此外, 由于模糊解是一个范围值, 只要清晰联盟支付被包含于模糊联盟支付中, 那么清晰分配解也一定包含于模糊分配解中.因此, 此解是经典A-T解函数关于支付函数的自然模糊延拓推广.今后将进一步根据实际问题探讨更加贴近现实应用的模糊合作博弈.