基于最小二乘法的热电偶电势非线性拟合*
2018-07-11郭晓聪
郭晓聪,李 宁
(中原工学院 信息商务学院,河南 郑州 451191)
0 引 言
温度是自然界中常见的一种物理量,在过程检测控制及工业生产中经常被用到,一般通过物体随温度变化的某些特性来间接测量。铸造生产中,需要测量温度,热电偶是常用的测温元件,需要查阅分度表获得温度,操作过程较繁琐,目前,国家对热电偶的应变和温度之间的对应关系并未给出标准的对应公式。
1 测温原理
两种不同成份的均质导体组成闭合回路,当接合点的温度不同时,回路中就会有电流通过并产生电动势,这种现象称为热电效应。两种不同成份的均质导体为热电极,温度较高的一端为工作端,温度较低的一端为自由端,热电势随着测量端温度升高而增长,它的大小只与热电偶材料和两端的温度差有关,与热电极的长度、直径无关;若热电偶冷端的温度保持一定,热电偶的热电势仅是工作端温度的单值函数,如图1所示,右端直接测量介质温度,为工作端(也称为测量端),左端为冷端(也称参考端),冷端与显示仪表或配套仪表连接,显示仪表会指出热电偶所产生的热电势[1-2]。
2 对分度表线性拟合的原因
如图2所示,两种导体A和B相接触,左端为热端,右端为冷端,由热电效应,该回路内产生热电动势,所产生的热电动势由接触电动势和温差电动势两部分组成。温差电动势是在同一导体的两端因其温度的不同而产生的一种热电动势,经推导,电动势的大小为以下所述。
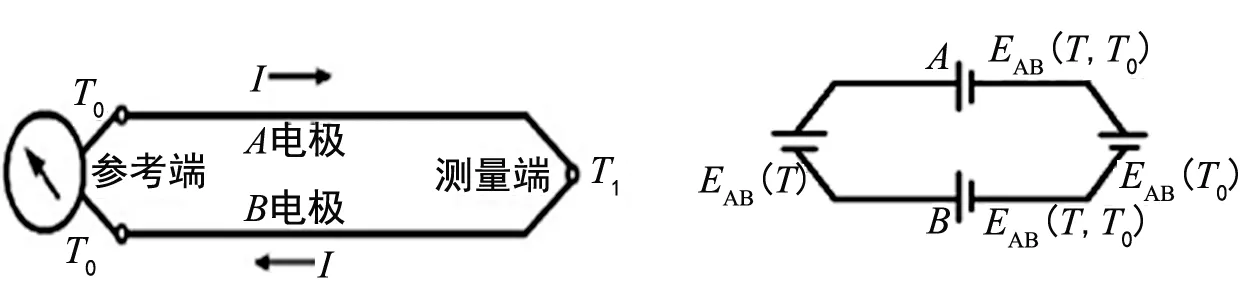
图1 热电偶工作原理图 图2 热电偶回路
接触电动势为:
总的热电势函数EAB(T,T0)
EAB(T,T0) =[EAB(T)-EAB(T0) ]+
[-EA(T,T0)+EB(T,T0)]
=K/e(T-T0) lnNA/NB+
总写法为:
EAB(T,T0) =α(T-T0)+β(T-T0)2+…
由总写法式知,电势与温度之间的关系函数包含了积分,且是多项式,呈非线性,且其非线性误差大多为1%以上,需要对其进行拟合,找出拐点,使之用几个多项式表示,代替分度表存入微机。
3 拟合过程
若已知y=f(x)在n个点上的值如下所示,要求出该函数的一个近似表达式,最简单的是设所求的表达式为一个次数低于n的多项式,如[3]:
Φm(x)=a0+a1x+a2x2+…+amxm(m 用最小二乘法来确定方程中的全部系数aj(j=0,1,2,…,m),为此令: 经推导得: 拟合过程基于最小二乘法,用到软件MATLAB,此软件功能强大,编程简单,误差计算和查询界面选择Visual Basic 。 拟合阶段预分四阶段:第一阶段每100个点一个段,一共分16段,低温段超出的点较多,目的是找出比较合理的多项式次数;第二阶段根据每200个点一段,依据第一阶段的最高次数,进一步确定最佳次数,控制拟合精度,确定拐点个数;第三阶段分四段,每400个点为一段,这段要注意拐点多少,如果第二阶段高温拐点较少,那第三阶段分段就有意义,若第二阶段拐点较多,第三阶段意义不大,拐点和分段更多。第四阶段根据第三阶段的结果而定,最终确定最佳拟合次数和段数[4-8]。 拟合过程: ① 一次函数使用polyfit(x,y,1) ② 多项式函数使用polyfit(x,y,n),n为次数,以第一阶段为例指数4次为例 x=[0,1,2,3,4,…,100]; y=[0.000 0.005 0.011 0.016 0.022,…,0.643]; p=polyfit(x,y,4) f = polyval(p,x); plot(x,y,'o',x,f,'-'); 这种算法得出的误差在Visual Basic界面中显示,如图3所示,均在误差范围之内。 图3 每段误差值 经分析,前三个阶段共同点:4次、5次拟合出来的曲线非常不准确,MATLAB 警告给出次数不适合,所以第四阶段仅选2次和3次多项式进行比较。 第四阶段所得结果: 次数为2次时所得多项式为5段,结果如下所述: 第一段:-47.7700x2+181.3523x+0.0576; 第二段:-20.9425x2+164.6804x+2.7800; 第三段:-3.4289x2+126.8290x+24.5775; 第四段:-0.8028x2+103.6932x+81.2807; 第五段:0.3952x2+71.7563x+292.5307。 次数为3次时,结果如下所述: 第一段:27.8941x3-593630x2+182.6201x+0.0285; 第二段:1.1395x3-12.0436x2+146.9068x+104547; 第三段:0.0748x3-3.0423x2+124.4399x+22.7983 次数为三次时,第四阶段的结果仅为三段,前五个点超出误差范围,但由于0~5 ℃几乎不用,所以不再考虑,因此较合理,三段拟合曲线如图4所示。 生成可执行程序后,在程序中输入显示器的毫伏值,即可得到对应的温度,界面如图5所示。 图4 三次拟合曲线 图5 可执行程序 通过MATLAB和Visuai Basic 相结合的方法,将贵金属热电偶铂铑—铂热电偶的分度表拟合成三段三次多项式,并生成可执行程序,简化铸造车间工人工作量的同时也提高了工业自动化。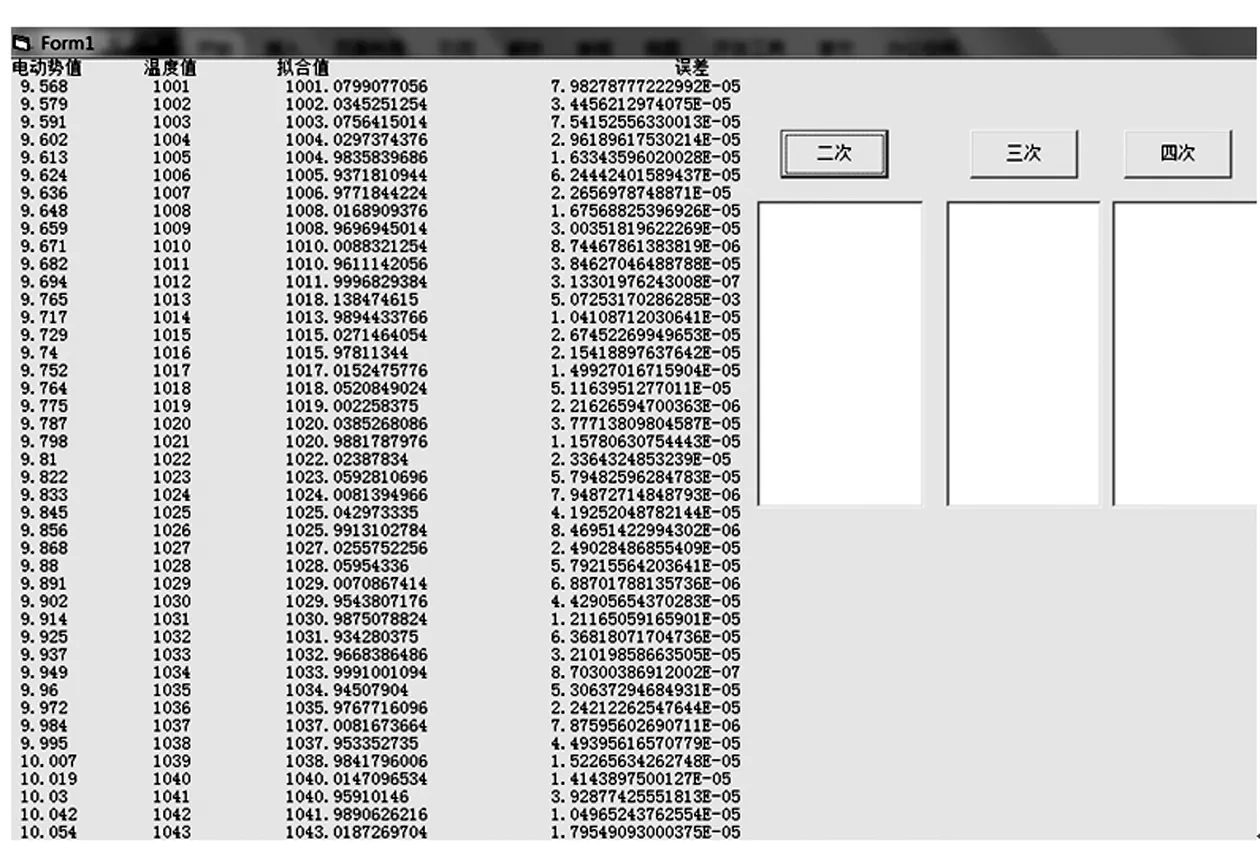

4 结 论
