波纹管流阻特性实验研究与数值模拟*
2018-07-11崔永龙赵术伟范荣超蒋彦龙
崔永龙,赵术伟,范荣超,徐 雷,蒋彦龙
(1.南京航空航天大学,江苏 南京 210016;2.航天晨光股份有限公司,江苏 南京 211100;3.金陵科技学院,江苏 南京 211169)
0 引 言
金属波纹管具有柔性好、减振降噪、使用寿命长等优点,被广泛应用于医疗、化工、船舶、航空等众多领域。目前,对金属波纹管的研究多集中于对其强度、挠度、传热性能的研究,而对波纹管流阻特性的研究相对较少。
S. Mahmud[1],C. C. Wang[2]分别针对不同的波型对雷诺数、设计参数对传热特性和流动特性的影响进行了研究。A. K. Tiwari[3]对两种不同流动介质通过波纹管的压降和传热性能进行了数值研究。D. C. Wiggert[4]采用静态与瞬态相结合的方法对波纹管内部的流动特性进行了研究。张凤玉等[5]以液氮和氮气为介质,研究了波纹管内压降和摩擦系数与雷诺数的关系。杨虎生等[6]对不同波形的波纹管的传热特性和湍流强度进行了比较。吴峰等[7]在层流及低雷诺数湍流工况下对波纹管管内流动与传热性能特性进行了数值模拟。俞慧敏等[8]对光滑圆管和螺纹型波纹管所形成的传热性能和压降差异进行了研究。
针对环形波纹管,通过对其进行流场仿真与实验研究,旨在获得波纹管弯曲半径、弯曲角度、入口压力对流阻特性的一般性影响规律,为今后金属波纹管的不断优化提供技术指导。
1 实验系统与测试原理
1.1 实验方案设计
实验采用的流阻测试实验台以水作为流动介质,以高压水泵作为动力源,由水箱、高压水泵、流量计、稳流管、压差传感器、实验金属软管和阀件组成。阀件有截止阀、流量调节阀和旁通阀三种。截止阀控制水箱供水,为了保证设备启动安全,处于常开状态。流量调节阀与旁通阀通过改变两者开度调节流量。旁通阀采用球阀,在大开度时,会导致实验过程中数据波动较大,实验中流动达到稳定的时间增加,所以旁通阀开度设置在20°~30°,并且保持常开状态。
序号8稳流管的长度应为管道直径的5~10倍,后部稳流管后面应设置软管接入水箱。压差传感器安装在序号8稳流管上,为确保实验管道的密封性,采用螺纹形式连接。

图1 流阻测试实验台原理图1.水箱 2.水泵 3.截止阀 4.旁通阀 5.流量调节阀 6.流量计 7.稳流管 8.稳流管 9.压差传感器 10.实验管
实验中在实验台上固定不同弯曲半径和弯曲角度的金属软管,并与稳流管连接,开启电箱与水泵进行实验。水箱中的水经泵作用从截止阀、流量调节阀到流量计前的稳流管。经过流量计,可以读取其体积流量并在PLC中以电流输出。再经过实验金属软管后回流到水箱,在实验金属软管前的稳流管处的压力传感器可以读取流入弯管段的压力,在实验金属软管前后的压差传感器读取弯管段压差,均以电流输出。实验中,通过改变流量调节阀和旁通阀开度改变流量,减小流量调节阀开度,增大旁通阀开度,降低流量,反之增加流量。旁通阀的开度增加会导致流量波动,所以可以减少旁通阀开度的调节,以流量调节阀的开度调节为主。
1.2 测试原理
在进行实验时,采用水作为流体工质,可看作不可压缩流体,因此实验管道内平均流速可由测得流量根据公式计算得到,公式如下:
(1)
式中:Q为管道内流量;d为管道水力直径。
从而可以计算出雷诺数Re:
(2)
式中:ρ为水的密度;v为平均流速;d为管道当量直径;μ为水的运动粘度系数。
管内流动的能量损失通常可分为沿程阻力损失和局部阻力损失,而在实际的工程实践中,通常将沿程阻力损失和局部阻力系数整合成一个系数,称之为综合阻力系数ξc,其计算公式如下:
(3)
由综合阻力系数可根据公式(4)计算出摩擦阻力系数λc:
(4)
文中所涉及的金属软管,其管内流动为湍流,流动状态复杂,管道粗糙度难于直接测定。通过实验获得不同流速下的摩擦阻力系数λ,再根据尼古拉兹公式计算即可获得管道粗糙度Δ[9]为:
(5)
2 数值计算方法
2.1 计算模型
基于Pro/E对波纹管进行建模,建立弯曲角度和弯曲半径的模型。所涉及的波纹管模型的波形示意图如图2所示。波纹管的波形特征尺寸及外形尺寸如表1、2所示。
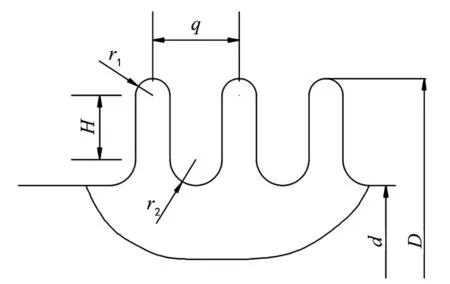
图2 波纹管波形示意图

表1 波纹管的波形特征尺寸 /mm

表2 不同波纹管模型的外形尺寸
基于ICEM对所建立的模型进行网格划分,所使用的模型涉及波纹管的弯模,结构较为复杂,故采用非结构化网格进行网格划分。由于近壁层的流动状态对研究至关重要,因而需要对边界层进行网格加密。生成网格后采用光顺法提高网格质量。检查网格质量,确保网格质量符合计算要求时将其导出。
2.2 计算边界条件与工况
基于Fluent对波纹管内流场进行求解。使用标准k-ε湍流模型模拟管内的流动状况,速度和压力耦合采用二阶离散式,收敛条件的各项残差均小于10-6。边界条件设置如下:
入口条件:设置为压力入口,入口压力为0.8 MPa。
出口条件:设置为压力出口,通过设置目标流量给定流量,目标流量为通过流速、当量直径换算所得到的质量流量。
壁面条件:设置为无速度滑移壁面。
水的物性参数:密度ρ=998.2 kg/m3,动力粘度μ=0.001005 kg/(m·s)。
3 结果综合分析
3.1 压力和流速分布分析
由图3~6可以看出,随着流动介质沿波纹管管道流动,压力、流速都有所降低,入口处压力和流速最大,出口处最小。因为流体在波纹管的渐缩段积聚能量,在波纹管的渐扩段释放能量,这种周期性的能量的积聚与释放伴随着能量的消耗;由管道纵截面云图可知,管道中部流速最大,由管道中部向四周流速逐渐降低,贴近壁面流速最慢。因为波纹管的波纹对流体流动有阻碍作用,产生了流动阻力,在波纹的波峰、波谷处产生局部旋涡,耗散能量,使流速降低。

图3 波纹管压力分布图图4 波纹管速度分布图
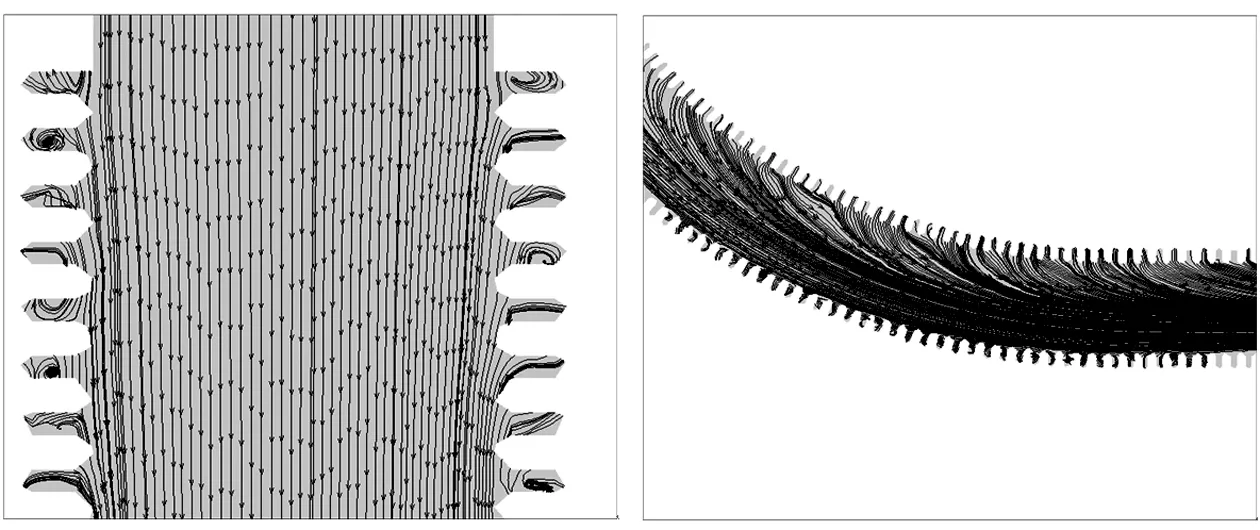
图5 直管段速度矢量图 图6 弯管段速度矢量图
与直管段相比,弯管段产生的压降更大。从速度矢量图及压力分布图可以看出,流体流经弯管段时,由于流体的惯性作用,流体流经弯管段时,来不及改变速度方向,外侧流速相对较大,压力上升,内侧流速较小,压力降低。波纹管弯管段的波纹结构会改变流体的流动状态,产生能量耗散。
3.2 入口压力对流阻特性的影响
实际实验中,很难保证入口压力为某一固定值,同时调节入口、出口阀门,可以维持入口压力接近某一固定值,但此工况下入口压力、流量和压差的波动较大,难以保证实验与仿真的边界条件相同。因此,进行了定入口压力与变入口压力实验的对比,实验结果的对比如图7、8所示。
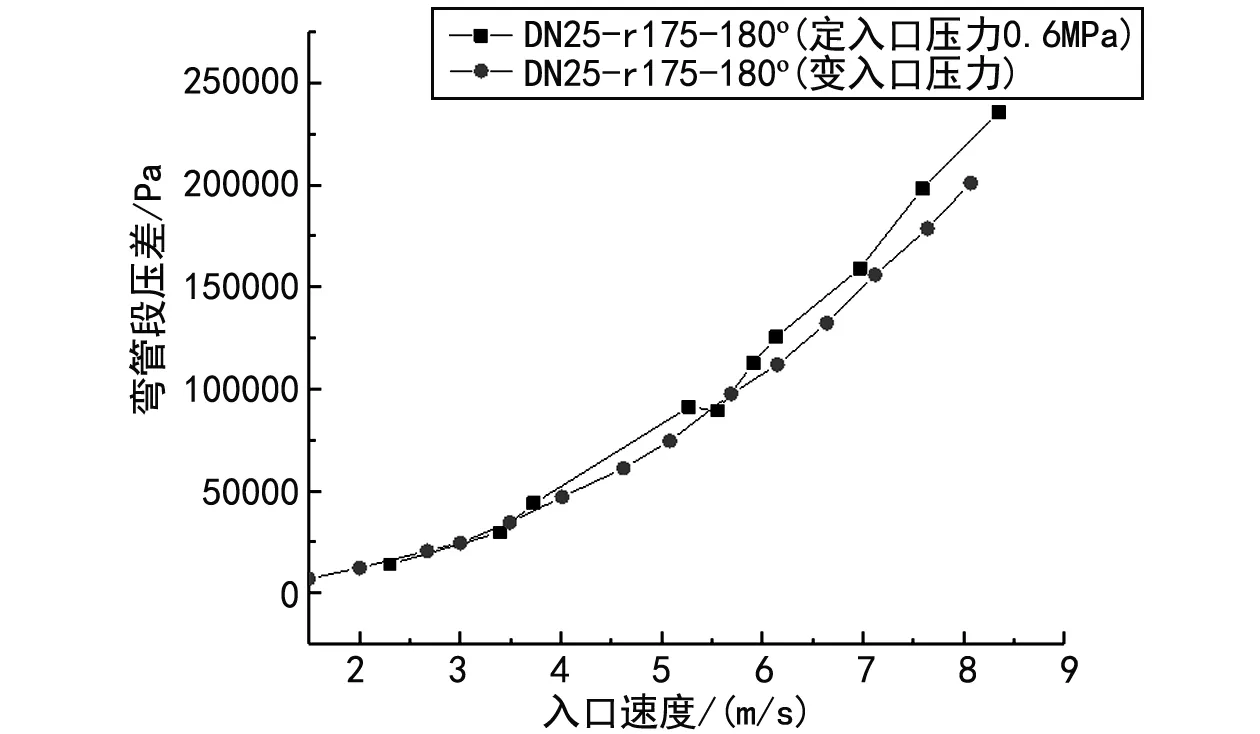
图7 变入口压力与定入口压力的压差随入口速度的变化(DN25,弯曲半径175 mm,弯曲角度180°)

图8 的变入口压力与定入口压力的综合粗糙度随入口速度变化(DN25,弯曲半径175 mm,弯曲角度180°)
由实验结果可知,与变压力入口相比,定入口压力工况下的压差和综合粗糙度的波动较小。因此,在确保流速满足要求的前提下,改变入口压力对实验的影响较小。当入口压力维持在0.6 MPa时,流量和压差存在波动,而入口压力对流阻特性参数的影响较小。因而,在误差允许的范围内,为降低实验操作的难度,实验过程中可以只调节入口阀门改变流速,此时的实验测量参数更为稳定,降低误差。
3.3 弯曲半径对流阻特性参数的影响
由图9可知,管道内部的流阻随着弯曲程度的增大而快速增加,弯曲程度大的波纹管内部流体出现了更加复杂的流动特征,如涡流、二次流等,因而压降和流阻随之变大。由图10、11可知,综合摩擦阻力系数和综合粗糙度均随着弯曲半径的增加而降低,且变化幅度逐渐减小。
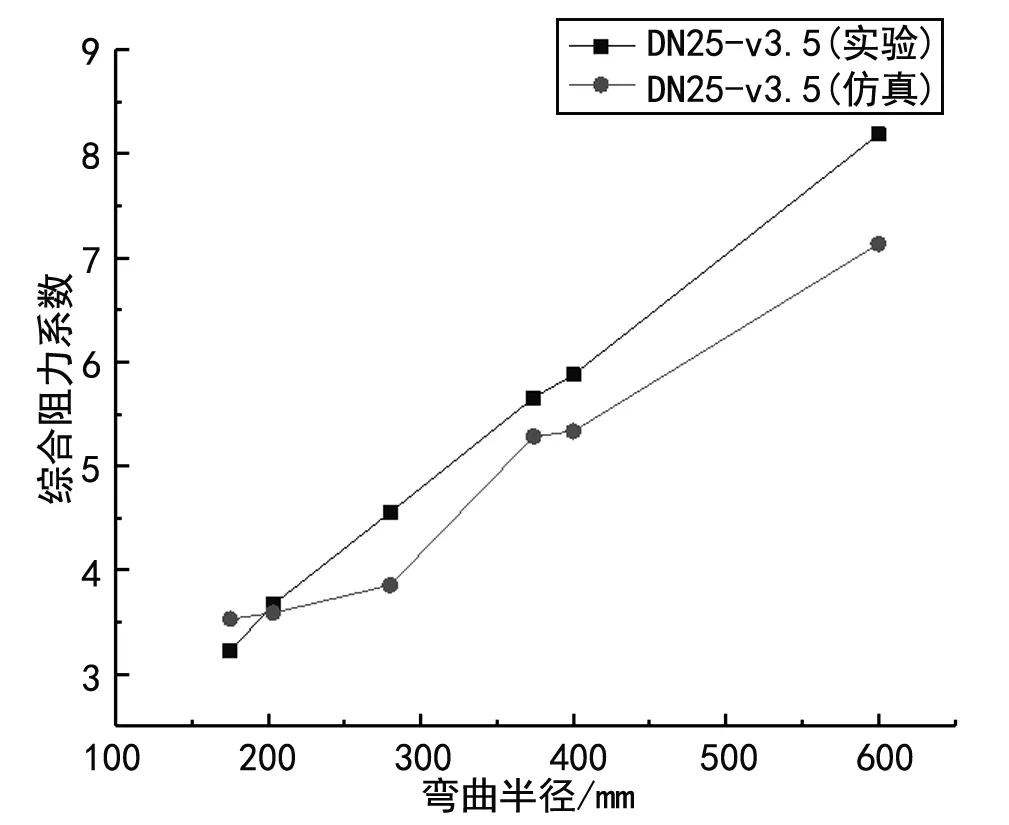
图9 综合阻力系数随弯曲半径的变化(DN25,弯曲角度90°,入口速度3.5 m/s)
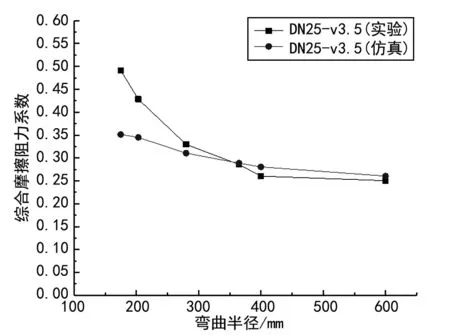
图10 综合摩擦阻力系数随弯曲半径的变化(DN25,弯曲角度90°,入口速度3.5 m/s)
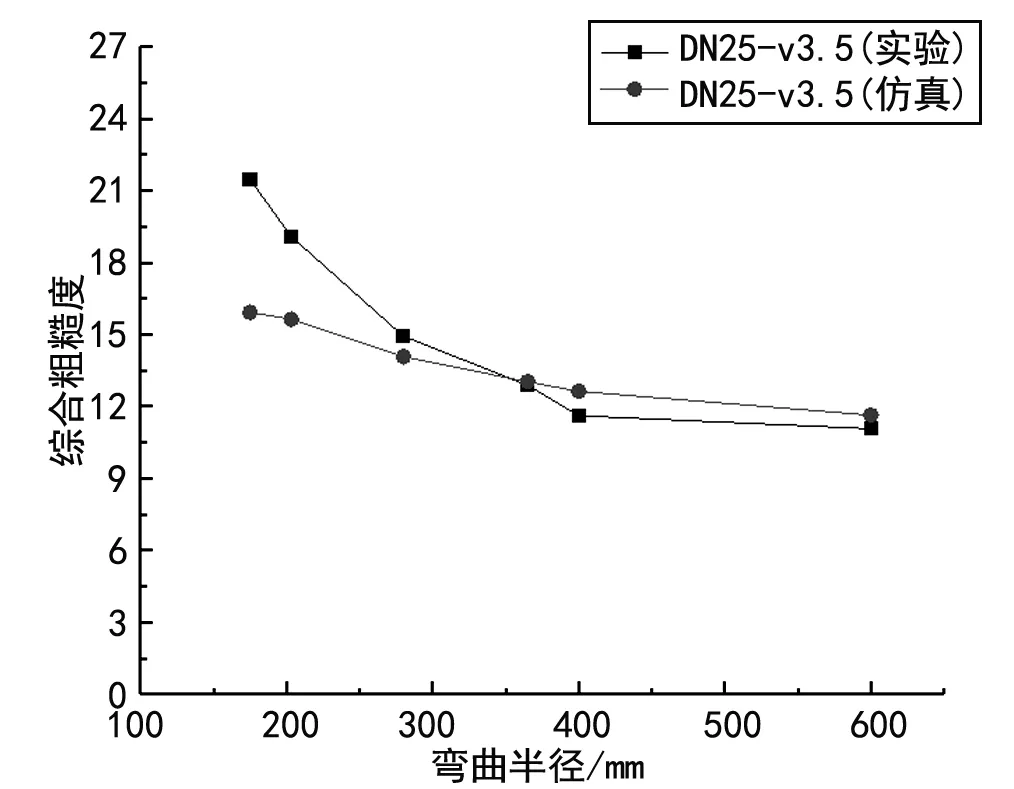
图11 综合粗糙度随弯曲半径的变化(DN25,弯曲角度90°,入口速度3.5 m/s)
通过对实验和仿真获得的结果进行分析,两者获得的结论一致,验证了仿真的正确性。
3.4 弯曲角度对流阻特性参数的影响
相同弯曲半径下,弯曲角度为180°的弯管相当于将两个90°弯管相连,仿真实验结果显示弯曲角度对综合摩擦阻力系数和综合粗糙度影响较小。而对于其余不同弯曲角度,则相当于将其中一个弯曲角度的弯管进行对管长的微分和积分处理。
由图12~14可知,综合阻力系数随着弯曲角度的增大而增大,而弯曲角度的变化对综合摩擦阻力系数和综合粗糙度较小。在实验误差允许范围内,实验与仿真均显示弯曲角度均对综合摩擦阻力系数和综合粗糙度影响较小。
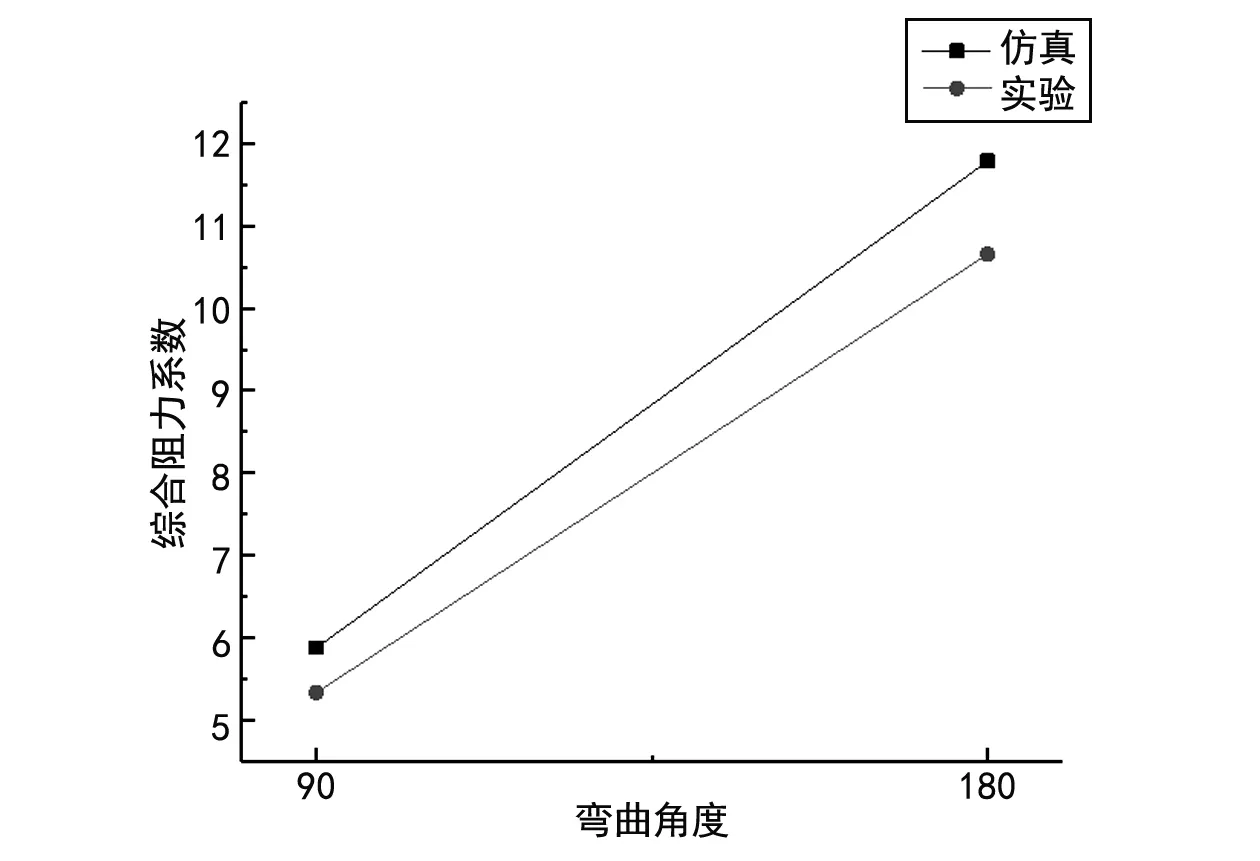
图12 综合阻力系数随弯曲角度的变化(DN25,弯曲半径400 mm,入口速度3.5 m/s)
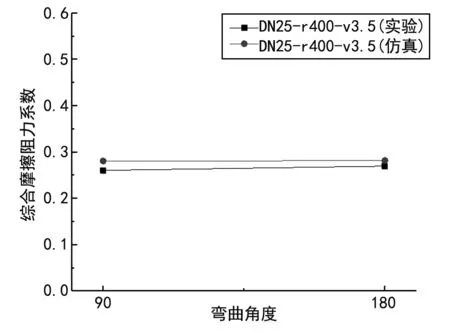
图13 综合摩擦阻力系数随弯曲角度的变化(DN25,弯曲半径400 mm,入口速度3.5 m/s)
4 结 论
通过对波纹管流场进行仿真和实验研究,得出如下结论:
(1) 在满足流速大小的前提下,入口压力的大小对流阻特性的影响较小。
(2) 相同入口速度和弯曲角度下,金属软管的弯曲半径的改变对综合摩擦阻力系数和综合粗糙度影响较大。弯曲半径增加,综合摩擦阻力系数和综合粗糙度降低。弯曲半径增加,综合阻力系数近似呈线性增加。
(3) 相同入口速度和弯曲半径下,金属软管的弯曲角度变化对综合摩擦阻力系数和综合粗糙度的影响较小。弯曲角度变大,综合阻力系数随之增大,综合摩擦阻力系数和综合粗糙度微幅增加。
