一种体质测试数据异常检测融合算法

白王梓松，刘 新，侯 岚，李亭葳

（1.湘潭大学 信息工程学院，湖南 湘潭 411105；2.湘潭大学 公共管理学院，湖南 湘潭 411105）

一、引言

大学生体质健康测试是根据教育部颁发的《国家学生体质健康标准（2014年修订）》所进行的全国性的大学生身体素质情况检测。目的是促进学生加强体质锻炼，养成良好的锻炼习惯，提高自身体质健康水平。该测试实行多年以来，为提高我国大学生体质水平起到了积极的作用。体质测试成绩是反映学生体质水平的重要数据，对该数据进行分析研究可以了解大学生整体的体质健康状态，发现不足，预测学生健康发展趋势，从而更好地指导大学生进行体育锻炼。

我们在对体质测试数据收集和处理过程中发现，由于学生作弊、流程不规范、设备误差、人为修改、学生消极懈怠等因素，收集到的部分数据是不真实、不准确的，不能真实反映学生的体质水平，对研究工作造成了一定的干扰[1-4]，因此对异常数据的检测十分必要。

异常检测在体质测试数据的具体应用中也可以称为体质测试数据的离群点检测，而目前离群点检测技术主要有基于统计方法、基于邻近方法、基于分类方法、基于聚类方法几种类型[5]。其中基于邻近方法可以分为基于距离和基于密度的离群点检测方法，现今比较常用的主要是基于距离方法、基于密度方法和基于聚类的方法。Zhang[6]等人使用基于距离的LOF算法对智能配电网故障进行检测；Lv[7]等人将基于密度的离群点检测技术运用到复杂数据集中；Fabian[8]、郁映卓[9]使用k均值聚类算法检测人体运动特征的异常行为。但以上各类异常检测技术都不能完全适用于具有多维、少样本时序等特性的体质测试数据的异常检测中。

本文针对体质测试中各种情况产生的异常数据的问题，以体质测试成绩系统为平台，综合k均值聚类算法、基于距离的异常检测思想、基于密度的异常检测思想，结合学生的历史数据，提出了一种体质测试数据异常检测融合算法（Anomaly Detection Fusion Algorithm for Physical Fitness Test Data，简称 ADF-PFT），以便对异常数据进行重测、剔除等进一步处理。

二、体质测试数据的特征

根据《国家学生体质健康标准 （2014年修订）》（简称《标准》）对大学生体质健康测试的要求，需要对学生BMI、肺活量、50米跑、1000米跑/800米跑、立定跳远、坐位体前屈、引体向上/一分钟仰卧起坐进行测试。根据《标准》中的要求和高校体质测试的具体实践，总结出体质测试数据有如下特点：①多维性；②各项目计量单位不同，数据值域范围差别大；③有历史数据参考。

按照《标准》对总分的计算方法，学生的体质测试总分由多个子项目的得分按照不同权值相加得到。各个检测项目所评价的身体素质之间有着某些关联，对单个项目进行异常检测研究是片面的，对所有项目数据组成整体的异常检测才具备研究意义。表1中的成绩是某同学完整体质测试数据，如只对引体向上单个项目进行研究，会发现该同学引体向上成绩非常好，远超过平均水平，据此可能会判定该成绩是异常成绩。但实际分析各项成绩后发现，该同学各项成绩都非常出众，可以综合判断该同学身体素质比较好，因此引体向上的成绩也比较可信。整体研究就是多维数据研究，对多维数据的处理是需要解决的第一个问题。

表1 某同学体质测试数据

各测试项目的指标、评价内容、计量方式等的不同，导致测试结果的值域范围也不同，从而造成了在异常检测时值域范围大的项目对结果影响明显。如表2中，除肺活量和50米外其余项目成绩浮动都相同，但少量的肺活量浮动（1号数据）和大幅度提高的50米成绩（2号数据）欧式距离对比发现，1号数据的欧氏距离更大，这种直接计算的方式不符合异常检测的效果要求。为了平衡各项目数据值域范围不同造成的影响，需要运用一定的方法对数据进行标准化，使各数据既能在同一值域中浮动，也能不失去数据本身包含的信息，使用何种方法对数据标准化就是需要解决的第二个问题。

表2 不同项目数据浮动对欧氏距离的影响

人体体质变化的规律是循序渐进的，排除环境等的影响，个体的锻炼、饮食、生活习惯通常也比较固定，在短时间内身体素质大幅度变动的可能性较小，倘若能将历史数据作为异常检测的条件之一，将大大提升异常检测的效果。传统异常检测技术使用标准化的数据处理虽然可以解决多维性和值域范围不同对检测结果的影响，但是却没有将历史数据作为异常检测的因素，缺少了一种有价值的、可靠的参考依据，影响其异常检测结果的实际效果。

三、体质测试数据的预处理

1.数据清洗

使用体质测试成绩系统中的成绩导入功能，将原始测试数据导入数据库时，通常有部分不满足要求，不能直接计算成绩。主要有以下几类：①空白数据和缺项数据；②数据项有无关空白字符；③数据项中圆角半角符号混用；④学生班级异动；⑤可更新成绩。

对于空白数据和缺项数据、学生班级异动的情况，只存储于数据库中，不计算成绩是较好的处理方式；对②和③中涉及的问题，可以依据数据项逐条检测情况，将异常字符剔除或替换为规范字符；对可更新成绩数据，需要使用摘要算法比对成绩是否有变化，并判断成绩是提高还是降低，最终保留较高的成绩。

2.数据标准化

多维数据值域范围的不同对聚类、距离和密度的计算结果有很大影响。体质测试的各个项目所测试的指标不同，单位也不尽相同，数据值域的不同导致值域范围大的项目对异常检测的结果影响大，值域小的项目对结果影响小。本文提出的ADF-PFT算法对每个项目的权重要求是相同的，因而数据标准化也就势在必行。

目前数据标准化有多种方法，如小数定标标准化、最值标准化、Z-Score标准化等。小数定标标准化方法通过调整小数点的位置，使所有的维度的值域在[-1,1]上来达到标准化的目的。该方法直观简单、易于实现，但其不能完全消除不同维度间的权值差异。最值标准化方法是对各维度进行线性变换，使原来值域为[υmin，υmax]的项目值域落在上，该方法可以灵活指定，并且可以完全消除不同维度的权重差异，但该方法中离群点对值域范围影响较大，导致大多数值可能集中分布在一个较小的值域中，不适用于检测离群点的数据标准化中。本文采用Z-Score方法，该方法利用各维度的均值和标准差进行标准化，如公式1所示：

四、体质测试数据异常检测融合算法（ADF-PFT）

1.体质测试数据离群指数（PFT-OI）

本文提出一种针对体质测试数据异常检测的评价指标——体质测试数据离群指数（Physical Fitness Test Outlier Index，简称 PFT-OI）。 PFT-OI以 ADF-PFT 算法为核心，以Z-Score标准化的数据为基础，不仅考虑了学生测试数据在数据总体中的聚类结果，还将历史数据和当前数据的差距作为因素之一，结合基于距离和密度的异常检测思想，综合度量体质测试数据中的异常情况。

定义1：用T(xi)表示PFT-OI，用来度量离群程度，用公式2表示：

其中，α、β、γ 是权值参数，Simk如公式 3所示，表示当前年份体质测试数据使用k均值算法聚类的结果的相似度。

其中KMS(xi,x)表示在集合X中的xi节点在使用k均值算法聚类后的结果，也就是节点xi与其最近的聚类中心的欧式距离。在使用k均值算法聚类的过程中，通过用多组数据对k值的多次探测实验，得到不同k值下所有节点质心距离的平均值。通过图1可以看出，当k=5时是拐点，因而对于体质测试数据选取k=5是合适的。

图1 多组k均值聚类结果图

定义2：Dist(x,x*)表示x节点与x*节点的欧式距离，如公式4所示：

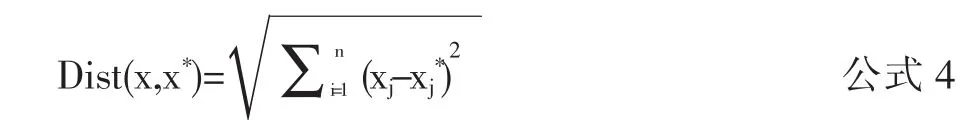
n为节点的总维度，j为维度标号。

Simdis是节点与历史数据距离的相似度，根据历史数据年份数y有不同的处理方式。当y=0时，说明没有历史数据，相似度为0；当y＞0时，需求出当前节点xi与之前多年数据距离的平均值，x*i,j表示所对应的第y年的数据节点。

Simden是节点与历史数据密度的相似度。本文定义表示当前节点xi与某年份对应节点的密度差，如公式6所示：

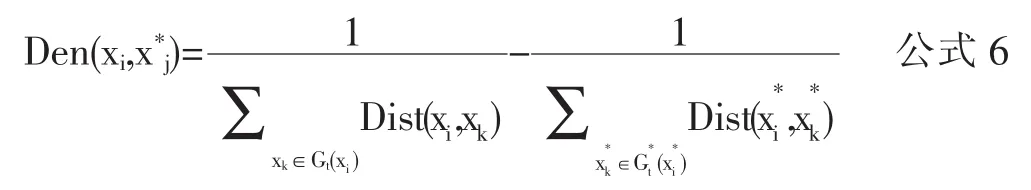
其中Gt(xi)表示距离xi最近的t个节点的集合，求出与xi最近的t个节点距离的和的倒数，可以反映出该节点的附近的密度。根据历史数据年份数y，Simden有不同的处理方式。当y=0时，说明没有历史数据，Simden为0；当y＞0时，应求出当前节点与其余各年份节点密度差的平均值公式如下：

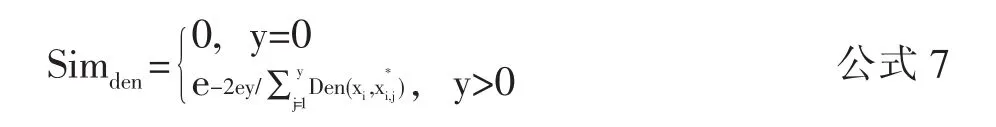
PFT-OI是根据体质测试数据的特点，专门针对体质测试数据设计的评价指标。它在对异常数据的检测中既能“横向的”考虑数据节点在本年度其他同学测试数据的结构，也能“纵向的”兼顾学生本人的历史数据，相比只使用聚类算法的优势主要有：较大程度提高了异常成绩的检出率；较大程度降低了误检率。

2.ADF-PFT算法步骤

输入：多年数据集 Y={X0,X1,X2,…,Xy}（其中 Xy={x1,x2，x3,…,xn}），聚类个数 K，邻近值 t，最大迭代次数 AtMax，权值 α、β、γ。

输出：PFT-OI集合 T={T(x1),T(x2),T(x3),…,T(xn)}

步骤1：随机选取K=5个点Xc={xc1,xc2,xc3,xc4,xc5}∈X0作为初始质心；

步骤2：对于X0中每个点求出dist(xi,xcj)min;i=1,2,3,…，n;j=1,2,…，K;令 λi=j；

步骤3：对于每一类的中心点xcj进行更新，计算λi=j 的所有点 Xcj各维度的平均值

步骤 4：如果迭代次数 At＜AtMax，At++，转到步骤 2；

步骤5：根据公式4，得到X0中各点到其聚类中心的欧氏距离集合D={KMS(x1,X0),KMS(x2,X0),…,KMS(xn,X0)}，按照公式3求出k均值聚类结果相似度集合，Simk={SK1,SK2,…,SKn}；

步骤 6：若 y=0，则 Simdis=0，转到步骤 8；若 y＞0，转到步骤7；

步骤 7：对于集合 Y={X0,X1,X2,…,Xy}，根据求出各集合X0与Xy对应点的欧式距离平均值集合按照公式 5 求出历史距离相似度集合 Simdis={SDI1,SDI2,…,SDIn}；

步骤 8：若 y=0，则 Simden=0，转到步骤 10；若 y＞0，转到步骤9；

步骤9：对于集合Y={X0,X1,X2,…,Xy}，求出每个点在对应子集合中的密度，即距离该点最近的t个点Xt(xi)={xt1,xt2,…,xtt}距离和的倒数 m=1/(∑xk∈Xt(xi)Dist(xi,xk)，Yden={M0,M1,…,My}，其中 M={m1,m2,…,mn}，求出各点与对应点密度差的均值按照公式 7 求出历史密度差相似度集合Simden={SDE1,SDE2,…,SDEn}；

表3 2015级2016年数据离群程度最大10个成绩（传统k均值算法）

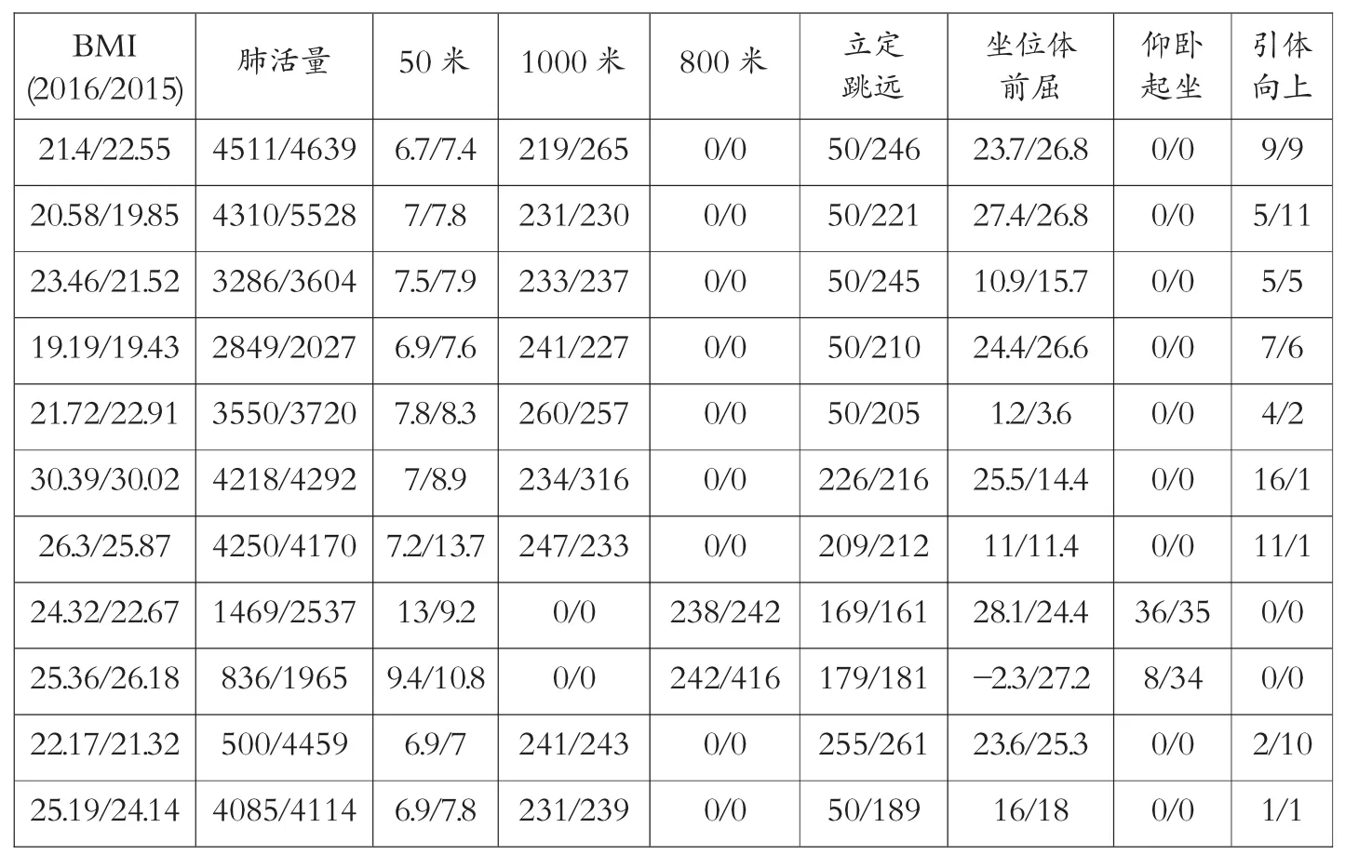
表4 2015级2016年数据离群程度最大10个成绩（PFT-OI）

步骤10：依据公式2可得到PFT-OI集合T={T(x1),T(x2),T(x3),…,T(xn)}。

五、实验结果分析

实验主要对比传统k均值聚类算法和PFT-OI两种方法对异常值的检测效果。

实验1采用某高校2015级4878名学生在2015学年和2016学年的体质测试数据作为数据集，其中男生占比 46.3%，女生占比 53.7%。取 α=1，β=0，γ=0，即传统k均值聚类算法对2015级2016年体质测试数据进行检测，T(xi)最大的10个同学具体成绩如表3所示。

根据k均值聚类结果的大小从上到下列出异常程度最高的10个结果。从表格中可以观察出：①有7个同学的立定跳远成绩为50cm，推测应该是设备问题导致；②第1条、第2条数据是异常程度最高的两个，但根据其2015年的成绩比较分析，这两位成绩稳定、合理，属于成绩极差和极好的同学，不应归为异常成绩，属于误检。

下面使用 PFT-OI，取 α=0.4，β=0.3，γ=0.3，得到 T(xi)最大的10个同学，他们成绩如表4所示。

根据T(xi)大小从上到下列出了异常程度最高的10个结果。从表4可得出：①除立定跳远成绩50cm异常的行外，其余各行都存在明显的成绩异常；②没有发现稳定、合理的极差成绩和极好成绩出现；③第6条数据只看2016年成绩时属于正常成绩，但同其2015年成绩相比时发现，其50米成绩和引体向上差距大，说明具有一定的异常性，用传统的k均值聚类方法不能检测出。

实验2使用某高校2014级2015年、2016年成绩和2015级2015年、2016年成绩分成若干小组作为数据集 （20000+条数据），取T(xi)较大的前1.5%的数据进行误检率统计，参数如表5所示。

表5 实验2参数设定表

由图2可知，传统的k均值聚类方法对异常成绩检测的误检率较高，PFT-OI相比传统的k均值聚类方法在误检率方面有明显的降低，尤其是当α=0.4，β=0.3，γ=0.3时，误检率达到较低水平。

图2 7组数据误检率统计图

使用相同数据集的情况下，从以上两个实验可以看出，PFT-OI相比于传统k均值聚类方法有较低的误检率，大大提升了异常检测的精度。

六、结束语

传统的k均值聚类方法对体质测试数据进行异常检测具有高误检率的缺点，PFT-OI和ADF-PFT算法的提出有效降低了误检率，完善了体质数据异常检测中缺乏纵向关系挖掘的问题。该方法现已着手应用到体质测试成绩管理系统中，在体质测试成绩分析和管理中可以有效辅助高校体育教师的工作，大大减轻工作量。

在实验过程中发现，ADF-PFT算法中还存在密度计算复杂度较高和权值优化难的问题，这也是笔者在下一步需要解决和研究的主要问题。