基于逆系统的空间飞行器末端控制方法研究

2018-07-11周新耀周藜莎臧月进

空天防御 2018年3期

周新耀，周藜莎，臧月进，曾　亮

(上海机电工程研究所，上海，201109)

0　引　言

空间飞行器是未来实现精确交汇的重要装备，这就要求飞行器自身具有极高的制导控制精度。末端控制技术可以通过导引律的设计，支撑飞行器在多变、复杂的空间环境下进行高智能交汇的要求，实现快速、稳定以及高精度的交汇任务。

针对空间飞行器的末端控制，传统的比例导引律虽然易于工程实现，但前向攻击能力差，难以满足交汇要求[1]。因此，国内外学者近年来多采用非线性控制理论对导引律设计进行相应研究，以提高空间飞行器对高机动目标交汇的鲁棒性，提高交汇精度[2]。其中逆系统方法就是用反馈线性化方法来研究控制系统理论的一种有效途径，是一种比较有效的非线性制导控制方法[3]。

本论文假定的飞行器末端执行机构由安装在质心位置的4个轨控发动机组成。针对轨控发动机推力特性，设计出一种基于动态逆系统方法的末端控制规律。通过求解弹目相对运动方程的逆系统，构建伪线性系统，再通过线性系统控制理论设计弹目视线角速度调节器，使得弹目视线角速度趋于零，可提高飞行器对大机动目标的末端精度。通过系统仿真验证，说明此设计方法是有效且正确的。

1　末端数学模型

1.1　飞行器数学模型

一方面，随着发动机的燃料消耗，导致飞行器的质量、质心位置、惯性张量随之发生变化，并产生一定的干扰力矩，同时对飞行器的姿态角产生相应的影响；另一方面，由于飞行器空间位置的改变，导致飞行器重力加速度也在不断变化。考虑上述因素的影响后，建立弹体坐标系下的飞行器运动数学模型为

(1)

rb=(mere+mrrr)/m(t)

(2)

Jb=Jbf-m(t)(rbTrbE-rbrbT)

(3)

(4)

(5)

qβ=arctan(-zr/xr)

(6)

(7)

其中，m(t)为飞行器质量随时间变化函数；mf为飞行器质量；me为空载时飞行器质量；mr为燃料质量;rb、re、rr分别为任意时刻飞行器质心、空载时飞行器质心以及发动机燃料质心在满载弹体系中的位置矢量；Jb为弹体系下的转动惯量；Jbf为满载弹体系下的转动惯量；E为单位阵；Fd为飞行器在地心发射惯性坐标系内受到的外力矢量；Gd为飞行器的重力在地心发射惯性坐标系内的矢量；Fz为发动机推力在满载弹体系中的作用力矢量；Mb为作用在飞行器的外力矩矢量；xr、yr、zr为飞行器与目标之间相对距离在惯性系各轴分量；qε、qβ为视线角；r为相对距离。在此，由于飞行器已处于末端飞行段，助推已抛掉，飞行器轴向为自由飞行状态，因此无轴向推力作用。

1.2　目标数学模型

目标为机动目标，建立弹道坐标系下目标运动学及动力学模型为

(8)

(9)

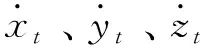
2　基于逆系统方法的末端控制规律设计

2.1　逆系统方法的一般理论

逆系统方法是用反馈线性化方法来研究控制系统理论的一种途径，是一种比较有效的非线性制导控制方法[4]。

逆系统的基本思想是：用对象的模型构成一种可用反馈方法实现的原系统的“α阶积分逆系统”，将对象补偿成为具有线性传递关系的且已经解耦的一种伪线性系统，然后利用线性系统的各种设计理论来完成对伪线性系统的综合控制[5]。

一般仿射非线性系统表达式为

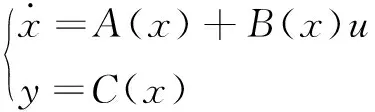
(9)

现以式(9)为例，按照逆系统方法来研究其控制过程。

式(9)中：x=(n×1)为状态向量；u=(m×1)为控制向量；y=(l×1)为输出向量；C=(l×n)为常值矩阵。

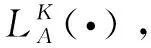
(10)

(11)

使用该记号来微分y的每个分量

(12)

令

(13)

(14)

则式(12)可化简为

y(d)=A*(x)+B*(x)u

(15)

系统(15)的逆系统存在的充要条件是B*(x)非

奇异。如果B*(x)非奇异[6]，则逆系统为

(16)

u=-F(x)+G(x)V

(17)

其中，

F(x)=[B*(x)]-1A(x)

(18)

G(x)=[B*(x)]-1

(19)

V=y(d)

(20)

这里，y(d)是逆系统的输入，u是它的输出。

对原系统式(9)施加逆动力学控制律式(17)，则原系统变为解耦的线性动力系统

y(d)+Pd-1y(d-1)+…+P0y=P0W

(21)

其中，W是新的外部输入，如图1所示。从而可以应用线性系统的各种设计理论来完成对伪线性系统的综合控制。

图1　逆系统原理图Fig.1　The schematic diagram of inverse theory

2.2　制导律设计

在弹目连线矢量方向上并不施加控制，而只是控制弹目视线角趋于定常值[7]，所以，选取状态量为

(22)

于是，有

(23)

(24)

选取输出

(25)

显然，y1、y2只需各微分一次即可出现控制量u1、u2，即

(26)

由式(22)～(25)，并对照式(16)可得

(27)

(28)

先将式(27)和(28)分别代入式(18)和(19)求得F(x)和G(x)，再根据式(16)、(17)求得末端的逆系统。并且

(29)

(30)

(31)

(32)

2.3　视线转率门限设计

为了避免出现发动机点火过于频繁的现象，本文设计了视线转率门限，当飞行器与目标间的视线转率超过门限值时，根据导引律和发动机点火逻辑开启相应发动机对飞行器进行控制，否则不对飞行器进行控制[10]。

(33)

(34)

在设计的过程中，主要考虑两个因素：一是得出的所需控制力与系统的实际推力之间的关系；二是系统视线转率与视线转率包络线之间的关系。

这种实际的控制律可以写成：

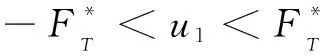
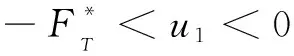
3　基于逆系统的空间飞行器制导控制仿真

假设弹目相对距离ΔR=30 km、相对速度ΔV=8 km/s、横向偏差ΔZ=5 000 m，目标采用正弦机动过载at=20·sin(0.4πt)(km/s2)。若采用比例导引，其末端精度为0.178 9 m。若采用逆系统方法设计的制导律，则末端脱靶量为0.016 38 m。大大提高了系统对机动目标的制导精度。具体仿真结果见图1～5。

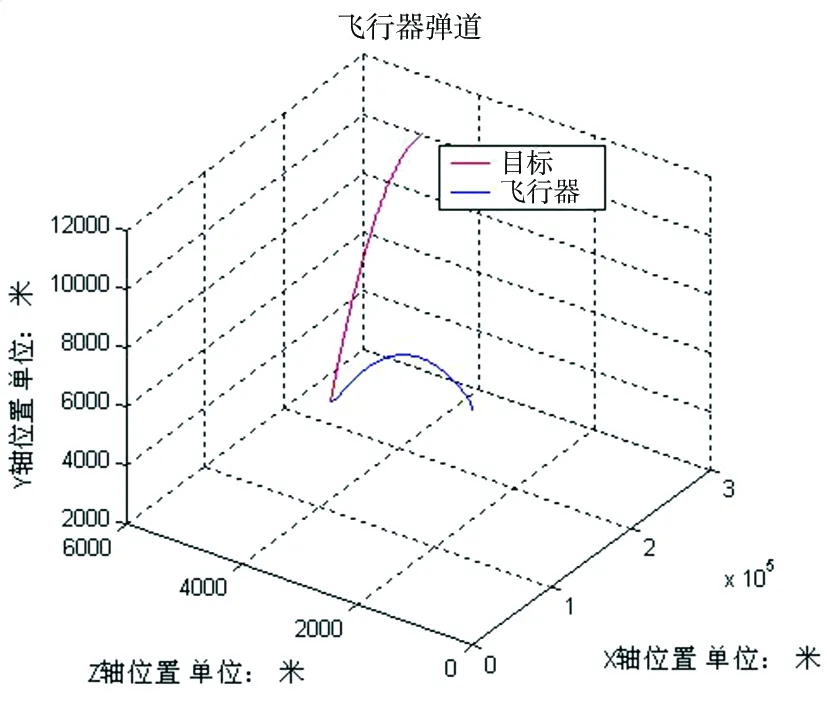
图1　弹目相对运动三维曲线Fig.1　The curve of missile-target relative motion

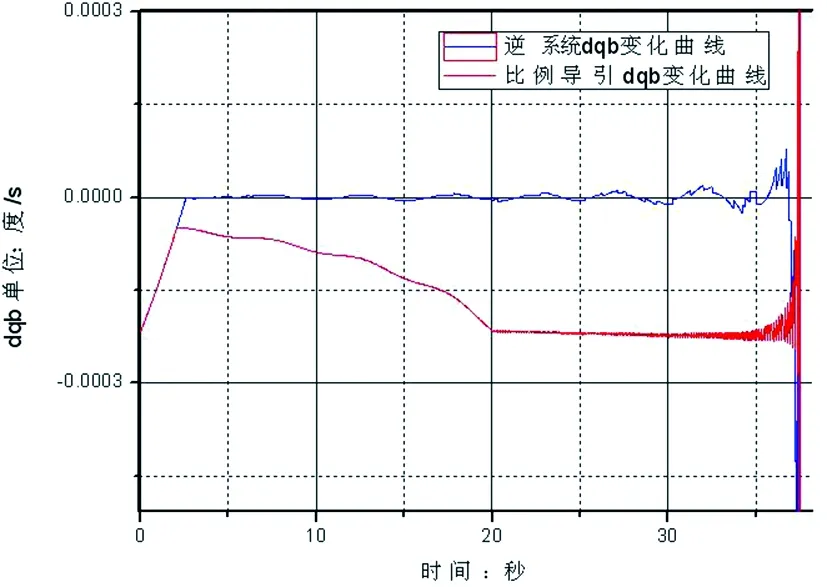
图2　逆系统方法与比例导引dqb对比曲线Fig. 2　The dqb curves comparison between dynamic inverse and proportional guidance

图3　逆系统方法与比例导引dqe对比曲线Fig. 3　The dqe curves comparison between dynamic inverse and proportional guidance

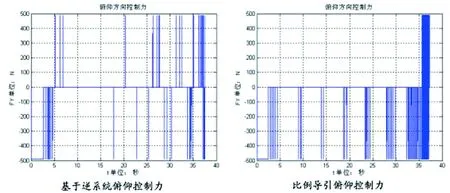
图4　逆系统方法与比例导引俯仰推力对比曲线Fig. 4　The pitching thrust curves comparison between dynamic inverse and proportional guidance

图5　逆系统方法与比例导引偏航推力对比曲线Fig. 5　The yaw curves comparison between dynamic inverse and proportional guidance

由图2～5的对比曲线可以看出，传统的比例导引控制律对于目标的机动过载响应滞后，在跟踪机动目标的过程中，视线角速率变化较为剧烈，导致发动机开关频率大大增加(由5 Hz变化到15 Hz)，从而导致弹体的不稳定，降低了飞行器的末端控制精度。同时，在比例导引的弹道末端，弹体会出现较大的跟踪过载，这也是比例导引控制所固有的缺点，会进一步影响对机动目标的跟踪精度和稳定性。

针对这种情况，采用逆系统方法对制导律进行改进，在目标做大机动的情况下，视线角速度变化相对稳定，弹道也较为平稳。同时，由于逆系统方法采用了反映目标运动的预测信息，可以提前对目标机动进行估计跟踪。因此，在飞行器飞行末端，相对比例导引方法而言，逆系统方法将轨控发动机的开关频率降低了。这样，一方面节省了燃料消耗，另一方面增强了末端的弹体稳定性，从而有利于提高末端跟踪机动目标的制导精度。