在抽象和具体之间寻找平衡点—浅谈小学数学学具使用

2018-07-11朱广琴

名师在线 2018年14期

朱广琴

（上海市徐汇区爱菊小学，上海　200030）

引　言

数学应该是抽象的，还是应该是具体的？新《义务教育数学课程标准》指出，数学是“对于客观现象抽象概括而逐渐形成的科学语言与工具”[1]。那么数学无疑应该是由抽象到具体的。如何具体，又如何抽象，是每个一线教师每天必须面对的实际问题。上海教育出版社出版（简称上教版）的小学数学教材，基本上每个新授的知识点在学习要求及活动建议部分都有“通过操作活动”或者“探索验证”这样的字眼，可见教材编写者也认为数学是源于生活，是对生活中规律的总结，并最终运用到生活中去的一门学科。

一、学具使用的中外比较

笔者在2017年曾有幸赴英国进行数学学科教学的交流，并在深入英国的小学开展课堂教学，同时也观摩了数学课堂，发现在英国的数学课堂中学具是无处不在的，他们对学具使用到了近乎依赖的程度，而且学具在课堂使用频率相当之高。

如五年级计算256÷7这样的算式，他们也是用学具来完成的。具体方法如下：先取出256的圆片（2个圆片100，5个圆片10和6个圆片1）除以7，首先看出2个圆片100不够平均分成7份，然后将2个圆片100换成20个圆片10，这样一共有25个圆片10，平均分成7份，每份3个圆片10还多4个，接着将多出来的4个圆片10换成40个圆片1，现在有46个圆片1，再平均分成7份，每份6个圆片1还多4个，这样得到256÷7=36……4。这是我在英国看到的真实课堂，他们就是这样热爱学具。你一定觉得不可思议，难道这样的算式不应该直接用竖式计算吗？这样的算法看似繁琐，但也并不是一无是处：它很好地诠释了这个算式的算理，尤其是余数后面落零的算理。

对照我们的教学，这样的算理似乎从来没有用这样“换算”的方式来实际探索过，我们将更多的精力花在了“商、乘、减、落”这样操作性的训练上面。如果问起学生算理来，学生会很肯定地说，就是这样算的啊！

我们在讲解这类算理的时候是不是可以使用学具呢？我们有没有可能在具体的学具和抽象的方法之间找到平衡点呢？

是不是我们的教材没有算理这一内容呢？答案是否定的。以上教版教材为例，第一次出现除法竖式是在三年级上学期（上教版《数学》三年级上P34），在教学除法算式之前，有专门的一段是用横式来讲除法算理的，而几乎所有竖式计算教学之前都有横式教学作为铺垫。由此可见，教材是很重视算理的，只不过很多一线教师在教学时总是忽略了横式算理的教学，而偏重竖式方法的教学。

二、新授课是学具使用的最佳时机

皮亚杰认为：“在教学过程中要通过儿童自身积极的活动，让儿童探究、发现知识。”因此，数学教学不应该只是机械地传授知识，而应该借助教具，设计丰富的活动，让学生积极参与进来，从而发展学生对数学的理解能力，激发学生对学习数学的兴趣[2]。这些数学活动，可以促进学生学习的主动性和对数学知识的运用能力，这也是课改一直关注的学生的创新精神。

从教多年来，我一直觉得教学是需要抓住时机的，而且一旦过了合适的时机，教学就很难达到最佳的效果了。新授课往往就是学习新知识的重要时机，所以学具的使用在新授课上常常有事半功倍的效果。

例如教学长方形面积时，可以使用小方格的学具让学生通过亲自数方格的方式推算出长方形的面积是由一行有几个面积单位乘有几行得到的，从而进一步推导出长方形的面积公式是：长方形的面积=长×宽。这个学生自己使用学具推导出公式的工作一定要在学生第一次接触长方形面积的时候进行为最佳。因为此时学生对于新的知识充满了好奇，并且在一张白纸的基础上推导更加能体验到公式带来的便捷性和实用性。反之，如果在上课开始就告知学生长方形的面积公式，学生有时会将其跟长方形的周长公式混淆，因为学生不是通过推导得来的，而是通过记忆得来的，这样的记忆有时候就会出现误差。如果出现误差时再回过去推导公式，收到的效果要比第一次接触时那种恍然大悟的感觉差远了。

以上教版小学数学为例，大部分新授内容都安排了学具教学，无论是计算类还是图形类，都讲究“画面感”，就是在解题时能够回忆起当时学习这部分内容时所使用的学具，从而形象地记住知识点。

例如在一年级学习20以内进位加法时，用小圆片的形式教学例题9+5，让学生在以后做到这样的题目时，脑海中都能有类似这样的图画（图1），或者这样的图画（图2）。

图1

图2

再如，在教学有余数的除法时，尽可能多地搭出某种图形的方式，来体验搭到不能再搭为止，从而理解什么叫余数要比除数小（图3）；还有用位置图上的小圆片理解什么是满十进一（图4）；用饼图来理解整体与部分，以及几分之一（图5）。这样的例子还有很多……

图3

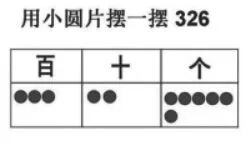
图4

图5

在小学阶段的教学中，形象的学具在帮助学生对知识点的理解上起到了不可替代的作用，我们一直讲要“学为中心”，要将“课堂还给学生”，学具的适当使用恰恰体现了这一理念。在教师的合理设计下，学生可以利用学具更好地理解数学知识，甚至自己通过学具也能推导出数学原理。这样学生会对知识达到深度理解，获得较好的学习效果，感受更好的学习体验。

三、在抽象和具体之间寻找平衡点

“让学生亲身经历将实际问题抽象成数学模型的过程”“动手实践、自主探索与合作交流是学生学习数学的重要方式”，这些课改的新理念已经深入人心，学具成为培养学生创作能力和动手能力的载体。在数学课堂中，学具的使用是非常必要的。一线教师要做的就是在具体的学具和抽象的知识之间寻找到平衡点。形象思维固然有助于理解，适时的抽象也是数学概括和简洁的体现。这也很考验教师的专业素养，比如厘清哪些内容在第几课时我们需要具体的学具操作、哪些内容到什么年级段需要提炼为抽象的结论。

新《义务教育数学课程标准》指出：要注意建立学生的“模型思想”。而“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的量关系和变化规律，求出结果并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识”。所以，我们在形象理解之后要注意引导学生抽象出数学模型，说到底数学是源于生活而高于生活的。