基于同态小波的乘性噪声去除方法研究
2018-07-10王明康周世健李志农王奉伟
王明康,周世健,李志农,王奉伟
(1.南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063;2.同济大学测绘与地理信息学院,上海 200092)
0 引言
在信号处理中,噪声通常被认为是对信号有害的,即它“污染”了信号。正因为噪声的存在,才产生了一系列的信号处理算法,使信号处理理论迅速发展。目前现有的一些信号去噪方法均是在加性类噪声(且默认为高斯白噪声)的基础上进行的。加性类噪声的消除方法有很多,如自适应滤波、经验模态分解方法等:自适应滤波是在维纳滤波、Kalman滤波等线性滤波基础上发展起来的一种最佳滤波方法;经验模态分解方法是为了精确描述频率随时间的变化而提出的一种自适应较好,直观的瞬时频率分析方法;小波变换是众多去噪方法中具有代表性的一种,信噪分离和弱信号提取是小波在信号分析中应用的重要方面。利用小波或小波包分解,可以将信号分解成不同的频段,从而实现信噪分离。
加性类噪声的信号是固定的,且噪声部分不随信号而变化,但是乘性类噪声则不同。乘性噪声往往由信道不理想引起,噪声部分随着信号的变化而变化[1]。因此,对于乘性噪声,利用传统的去噪方法很难得到理想的效果。现有的有效处理方法是引入同态变换去除噪声与信号的相倚性,将乘性噪声转化为加性噪声,再对信号进行滤波处理[2],此方法的去噪效果明显优于传统的去噪方法。联合同态映射与小波变换,提出一种基于同态映射与小波变换的乘性噪声消除方法,并进行仿真实验验证。
1 基于同态小波变换的乘性噪声消除方法
一般地,乘性噪声可用式(1)的数学模型表示[3]。

其中,y(t)表示含噪观测信号,s(t)表示真实信号,e(t)表示噪声,噪声类型为服从N(1,σ2)的高斯噪声。
首先由同态变换和小波阈值去噪两部分组成。首先,y(t)经过对数同态变换为 G(t)=ln(s)+ln(e)。这样就将原有的乘性噪声,在同态映射下已转换为加性噪声[4-5]。对于含加性噪声的信号,可利用小波变换方法对信号进行多尺度分解,选定门限阈值对小波系数进行量化处理,在每一尺度下把属于噪声的小波系数去除,保留并增强属于信号的小波系数,最后重构出小波去噪后的信号,运用指数逆变换恢复真实信号,文章选取信噪比和均方根误差2个指标对去噪效果进行评价。具体流程如图1所示。

图1 算法流程
小波去噪存在小波基和阈值的选取问题[6-9],如何选取最优的小波基和阈值以达到提高去噪、准确提取信号的目的也是很多学者研究的对象。这里小波基选取Daubechies小波,小波阈值采用软阈值法,将信号小波系数的绝对值和阈值比较,小于或等于阈值的点置零,大于阈值的点变为该点与阈值的差值,见式(2)。
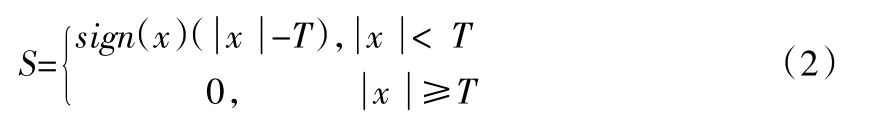
2 仿真实验分析
为了验证该乘性噪声消除方法的有效性,对仿真的3种非线性非平稳信号(bumps,blocks和 x(t))进行测试(对 blocks信号进行平移处理,使其幅值全为正值),其中信号采样点数为1024点,则有式(3)。
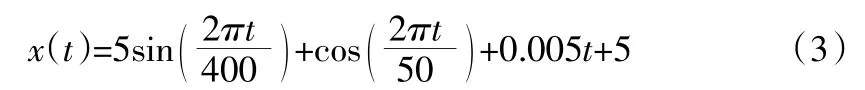
均方根误差 RMSE(Root Mean Square Error)见式(4)。
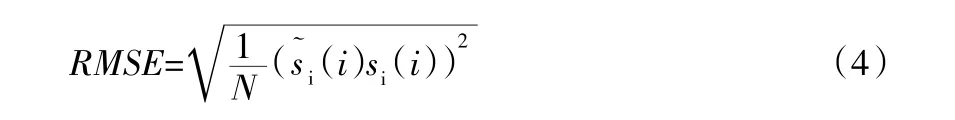
(2)信噪比 SNR(Signal-Noise Ratio)见式(5)。

其中SNR单位为dB。
采用Daubechies小波函数进行去噪处理。原始信号和加入噪声的3种信号见图2,含噪信号经处理后的结果见图3。利用MATLAB仿真3个含有乘性噪声混叠观测信号,并添加相同强度的噪声,通过小波阈值函数直接对含噪仿真信号处理和文中方法对含噪仿真信号处理2种方法进行去噪。小波去噪采用db6小波基,分解层次4层,根据第1层的高频系数估计噪声标准差σ,然后对含噪信号进行阈值处理。
图2是3种仿真信号的模拟序列,噪声已“污染”整个信号,需采用信号处理方法去除噪声的干扰,恢复有用信号。表1中,bumps信号经小波变换和文中方法处理后,信噪比分别为10.434 6 dB,14.572 4 dB;blocks信号处理后信噪比分别为14.729 0 dB,15.266 1 dB;x(t)信号处理后信噪比分别为14.294 3 dB,15.316 6 dB,可以看出信噪比明显提高。图3和表1结果表明,该方法在某种程度上实现了原始含噪观测信号中乘性噪声干扰的消除,较传统的小波变换或自适应滤波去噪有一定优势。
3 结语
针对乘性噪声去除问题,提出基于小波阈值处理的对数同态变换法。相比于其他方法,该法在去除乘性噪声方面效果明显,表明对于乘性噪声的去除,同态变换过程是有必要的。仿真实验中,bumps信号由小波阈值去噪处理后,信噪比与均方根误差分别为10.434 6 dB主0.541 3 mm;由该方法处理后,信噪比与均方根误差分别为14.572 4 dB和0.336 2 mm。结果表明,该方法较小波变换去噪有一定优势。此外,该方法实现简单,可直接处理时频域信号。因此,在含有乘性噪声的信号处理领域有较大应用潜力。
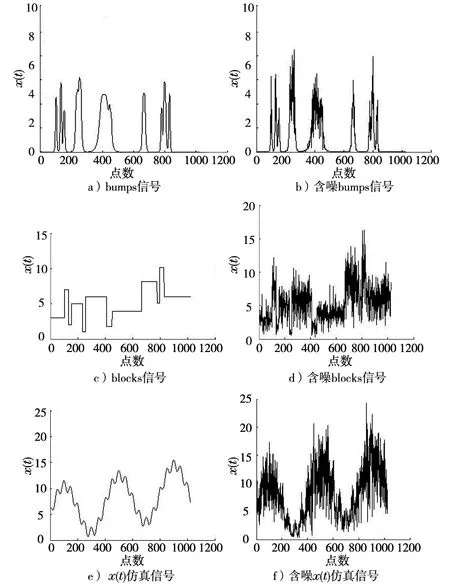
图2 模拟仿真序列

图3 小波阈值去噪与文中方法去噪结果
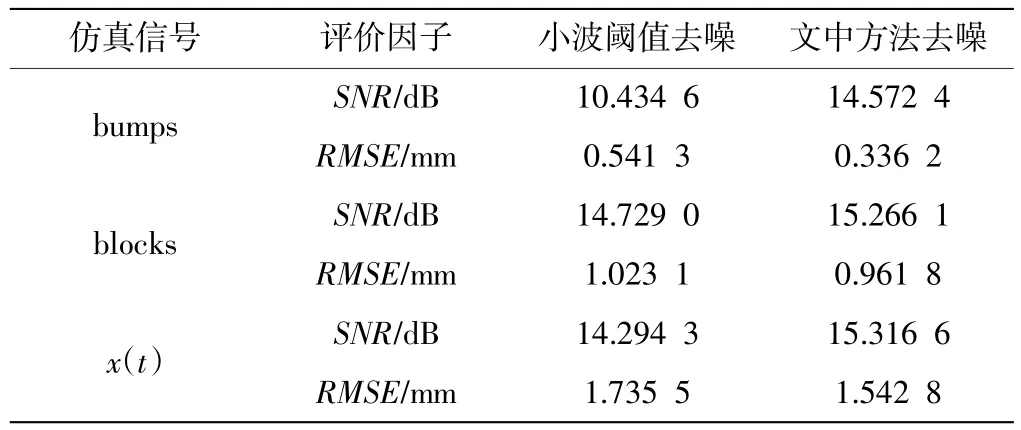
表1 3种仿真信号的去噪结果
[1]T.Teuber,A.Lang.A new similarity measure for nonlocal filtering in the presence of multiplicative noise[J].Computational Statistics and Data Analysis,2012,56(12):3821-3842.
[2]蒋立辉,李宁,成向阳,等.基于一种新的同态滤波算法的散斑噪声压缩[J].激光与红外,2002,30(1):11-14.
[3]Dong Y,Zeng T.A convex variational model for restoring blurred images with multiplicative noise[J].SIAM Journalon Imaging Sciences,2013,6(3):1598-1625.
[4]焦卫东,杨世锡,钱苏翔,等.乘性噪声消除的同态变换盲源分离算法[J].浙江大学学报(工学版),2006(4):581-584,614.
[5]焦卫东,蒋永华,林树森.基于经验模态分解的改进乘性噪声去除方法[J].机械工程学报,2015,51(24):1-8.
[6]关履泰.小波方法与应用[M].北京:高等教育出版社,2007:35-37.
[7]彭自然,王国军.用小波变换对ECG信号进行去噪研究[J].信号处理,2017,33(8):1122-1131.
[8]Donoho D L.Denoising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,11(3):613-627.
[9]毛建东,华灯鑫,王玉峰,等.基于小波包分析的激光雷达信号消噪算法的研究[J].中国激光,2011,38(2):226-233.
