深部采场工作面围岩应力分布规律及围岩破坏范围研究

耿宏波 叶义成 罗斌玉

（武汉科技大学资源与环境工程学院，湖北武汉430081）

大规模深部开采已成为我国采矿工业发展的必然趋势［1］，但随着矿山开采深度不断增加及开采条件日趋复杂，深部采场矿山压力理论及其应用研究成为众多学者研究的热点和难点之一。在深部煤层开采中，准确地了解采动后围岩应力变化规律和分布特点可为保护层开采时分析对被保护层的影响以及卸压开采提供理论基础；同时了解深部围岩破坏范围可用于分析底板运输巷道受采动的影响程度，为矿山安全管理以及围岩控制提供理论指导。

对于深部煤层开采后的围岩应力分布，大量学者运用试验研究、数值模拟以及现场测试等方法和手段从不同角度进行了研究，取得了一系列成果。刘万荣等［2］对深埋隧洞围岩稳定性进行了分析，推导衬砌支护反力与洞壁周边位移的解析表达式，得到围岩和衬砌支护特征曲线。耿琳［3］对深部采场基本顶垮落数值模型和力学模型进行了研究，得到了离煤层越远，采动对煤层支承压力的影响越小；刘书贤等［4］采用理论分析、模拟试验和数值计算相结合的方法，研究了深部煤矿开采过程中上覆岩层移动变形与应力场变化情况；宋艳芳等［5］数值模拟了孤岛工作面应力分布情况，得到了孤岛工作面的上下两区段煤柱分别承受着孤岛工作面上覆岩层的重量，处于高应力集中状态；史红等［6］基于微地震监测技术研究了覆岩多层空间结构倾向支承压力，用力学方法，针对倾斜煤层研究倾向支承压力的动态分布规律和计算方法，得到了倾向支承压力的计算公式；刘金海等［7］对新巨龙矿井1301工作面走向及侧向巷帮煤层垂直应力进行了实测，得到了深井特厚煤层综放工作面走向支承压力峰值位置到煤壁的距离及巷帮煤层侧向支承压力峰值位置到巷帮的距离比一般工作面大；唐军华等［8］通过数值模拟、X光衍射、扫描电镜、现场实测等手段，研究了两淮矿区不同采深和采厚情况下回采工作面前方支承压力分区变异特征；周钢等［9］采用空心包体应力测量技术，在原岩地应力实测基础上监测采动应力的演化过程，探究采动应力影响下工作面覆岩及巷道围岩应力的动态变化规律；程家国等［10］对深井高地压坚硬顶板采场围岩特性进行数值模拟研究，认为深井条件下围岩的受力情况更加复杂，围岩更容易出现应力集中；刘杰等［11］对深部采场工作面采动应力场实时监测，研究了深部工作面走向和倾向应力分布及变化规律，并分析了应力对煤层稳定性及动力现象的影响；Chaoru Liu［12］通过对深部采场应力分析得到水平最大主应力与垂直应力之比在0.63～2.42之间。胡建华等［13］还建立了深部采空区尺寸效应的危险度正态云辨识模型。

综上可知，对于深部工作面应力分析主要以实测和数值模拟为主。当对深部矿岩体进行开挖时，很难对实际应力进行检测，力求探索一种行之有效的方法对围岩应力进行初步计算，而运用微观裂纹扩展分析方法来分析宏观采场围岩应力变化的研究并不多见。基于此，在课题组前期研究基础上［14-16］，运用断裂力学理论，将深部煤层开采工作面从开切眼推进至一定距离的采空区长度视为无限大岩体垂直剖面内一条裂纹，借用无限大板内裂纹端部应力分布分析方法来研究工作面围岩应力变化规律，在此基础上，进一步研究得到深部工作面前方煤层破坏距离和底板破坏深度。研究可为地下深部工程设计的应力及围岩破坏距离初步计算提供一种思路。

1 深部采场围岩应力计算

1.1 围岩力学模型

深部煤层开采时，开采煤层厚度一般远小于开采宽度。假如回采工作面从开切眼开始，工作面推进距离在横向地应力分布不大，满足裂纹平面问题的应力均布条件。可将采空区剖面假设为无限大岩体内部一条裂纹，并简化成平面问题来分析。

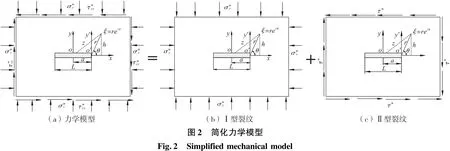
对深部任意倾角的煤层，煤岩体受到多向压力作用。从开切眼起，随着回采工作面不断地向前推进，直接顶悬露的面积增大，当顶板出现初次垮落，此时设工作面推进距离L=2a，建立受压状态下的力学模型，如图1所示。模型受到无穷远处垂直应力σ=γH和水平应力λσ的作用，γ为岩体容重，H为上覆岩层的深度，λ为侧压系数。β为λσ与x轴夹角，x，y为直角坐标系，x轴与煤层倾斜方向重合。

利用坐标变换的方法得到图1坐标系里远场应力分量为

此时，力学模型可等价转化为图2（a），以下记而图2（a）的力学模型可等价于图2（b）（I型裂纹）与图2（c）（II型裂纹）的线性叠加。

1.2 采场应力计算

引入Westergaard应力函数对图2的力学模型进行计算。图2（b）所示的Ⅰ型裂纹采空区的Westergaard应力函数［17-18］为

其中，

为Westergaard函数，B为待定常数。并记表示它的积分。设

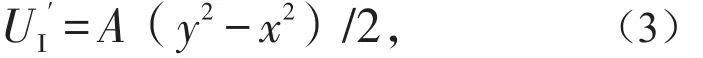
其中，A为待定常数，与远场边界条件有关。根据解析函数的性质，其导数和积分仍为解析函数。因此，应力函数与应力分量之间的关系应满足：

根据边界条件，当 z→∞时以及裂纹前缘坐标z=a+reiθ=a+ζ可得到只保留奇异项的应力分量为

式中，o（r-1/2）表示比r-1/2更高阶的小量。

图2（c）所示的Ⅱ型裂纹采空区边界条件为：当z→∞，在裂纹表面上（y=0，此问题的特点是反对称于x轴，与I型方法相似，取

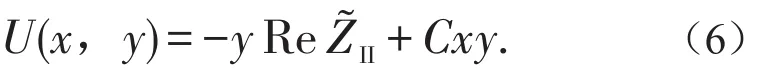
代入式（4），得到II型裂纹应力为

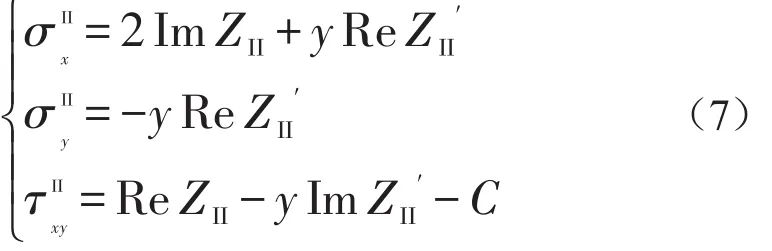
ZII称为II型裂纹的Westergaard函数，可取：

根据无穷远处的边界条件，得到C=D=-τ∞，因此式（8）可以写成：

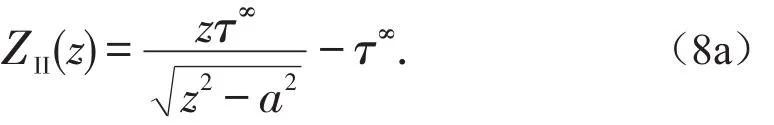
将式（8a）代入式（7），不难验证完全满足内边界条件。仍采用裂纹前缘坐标z=a+reiθ=a+ζ。将式（8）代入式（7），并利用在裂纹端点附近r/a＜＜1的条件，可得此时裂纹端点附近的应力场为

2 采场围岩应力分布分析

根据上面的分析，采场工作面围岩的应力为

即

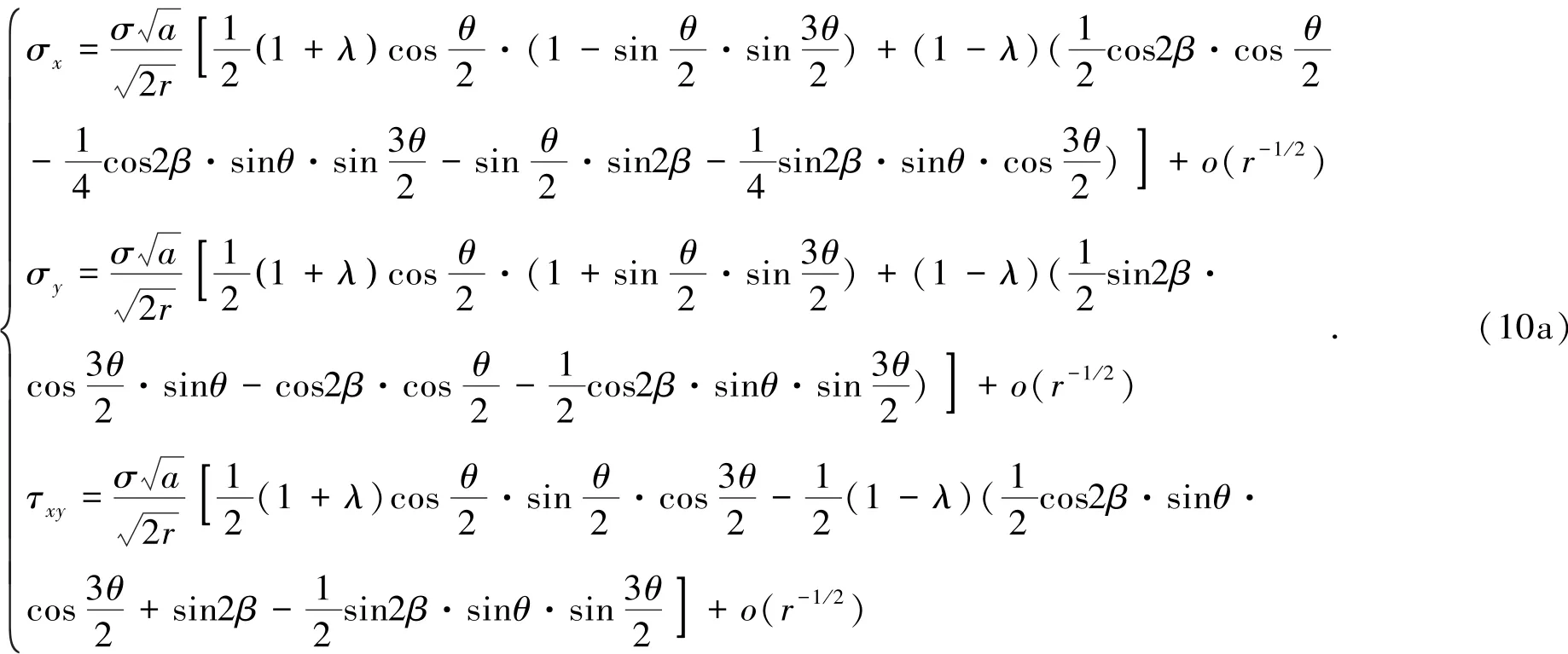
式（10a）即是任意倾角的采场工作面（即裂纹端部）围岩任意一点应力表达式。由式（10a）可知，采场工作面围岩应力分布与埋深H、工作面推进距离L=2a、煤层倾角β以及离采场工作面的距离x=rcosθ有关。

为方便分析，令

则式（10a）可表示为

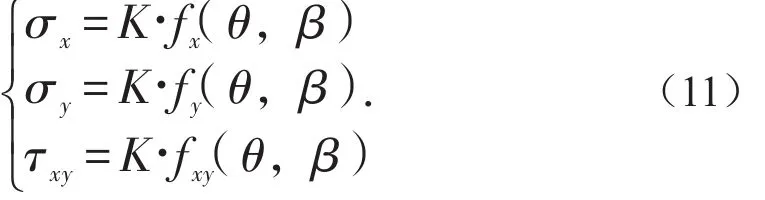
式（11）为深部采场工作面围岩应力场函数，由函数f（θ，β）和函数K组合而成，其中函数f（θ，β）表征应力的周期变化规律，函数K反应了应力的强度变化。为进一步分析应力分布情况，由于深部采场应力分析得到水平最大主应力与垂直应力之比在0.63～2.42之间［12］，取侧压系数λ=1.5。并设工作面推进距离L=2a=30 m，忽略高阶小量，绘制出β、θ∈［-90°，90°］，x=1～50 m，H=600～2 000 m的fx（θ，β），fy（θ，β），fxy（θ，β）以及K的三维函数图像，如图3～图6所示。

由图3可知，fx（θ，β）图像呈“马鞍型”，在θ=0°，β=±90°取得最大值，“马鞍”中点在θ=β=0°。而fy（θ，β）函数图像呈“驼峰型”，在θ=β=0处为“驼峰”中心，函数并非在此处取得最小值，而是在θ=±90°，β=±90°取得最小值；在θ=±45°，β=0°时函数取得最大值，如图4所示。fxy（θ，β）函数图像呈正反矗立的多峰型，且最大值与最小值之间互为相反数，如图5所示。K函数图像与离工作面的位置呈双曲线变化，离工作面越近，压力越大，压力随着离工作面距离呈曲线递减；压力随采深呈线性增加，如图6所示。由此可知，采场围岩应力不是简单线性分布，而是不断波动变化。

从应力理论计算结果和函数图形来看，表征应力周期变化的fx（θ，β）、fy（θ，β）和fxy（θ，β）函数图像均随θ、β改变呈现峰值与谷值交替变化。随着煤层倾角增大，煤层受到应力逐渐减小；反映应力强度变化的K函数随离工作面距离呈双曲线变化。实际开采中，工作面推进使得底板岩层在水平方向上分为采前集中应力压缩区、采后卸压膨胀区和采后压缩应力恢复区。这3个区在开采过程中于底板岩层内不断循环出现，使底板岩层处于闭合、张裂、恢复的循环变化之中。

3 工程案例验证分析

上述对回采工作面应力分布分析，得到了深部回采工作面前方应力表达式，为验证应力表达式的有效性，侧压系数仍然取λ=1.5。根据工程实际参数代入式（11）计算得到y方向的应力随离工作面距离的变化，并与案例实测数据进行对比分析。

刘杰等［11］研究了二矿庚20-21050回采工作面支承压力分布规律。煤层走向可采长度845 m，回采工作面倾向长176 m，采深740～850 m，煤层平均厚度1.9 m，煤的坚固性系数为0.3～0.5；工作面走向113°，倾向23°，平均倾角9.5°，实测了工作面前方煤层压力结果如图7（a）所示［11］。

由现场监测数据可知，应力最大值为29.8 MPa，如图7（a）。在未知岩层内摩擦角的条件下，经理论计算得到了工作面前方应力分布，如图7（b）所示。从图7（b）中可知，理论计算最大应力值约为33.2 MPa，比实测结果高2.4 MPa，相对误差为11.4%。

郑军［19］研究了在工作面采深500 m时的采场围岩应力分布，其中煤层走向长496 m，倾角2°～45°，平均35°，厚度1.5～14.5 m，平均8.l m，煤层普氏硬度系数为0.8，实测结果如图8（a）所示［19］。

根据实测结果可知，3#钻孔显示工作面超前支撑压力最大，其峰值为25 MPa。理论计算（图8（b））的结果显示，最大应力值为24.5 MPa，比实测结果小0.5 MPa，相对误差为2%，应力分布趋势与实测结果相似。

夏永学［20］研究了屯留煤矿S2202工作面矿压显现规律，所采工作面煤层为3#煤层，赋存于二叠系山西组地层中，埋深500～732 m，平均590 m，为陆相湖泊型沉积。煤层厚度较稳定，为5.34～7.25 m，平均6.24 m，煤层倾角为0°～14°，工作面支承压力实测结果图 9（a）所示［20］。

由图9（a）可知，8个钻孔应力计所测得的工作面超前最大支撑压力值为14.7 MPa，而理论计算峰值（图9（b））为16.5 MPa，比实测结果高1.8 MPa，相对误差为12.24%。

工作面前方应力理论计算结果与3个实例实测结果，见表1。

由表1分析可知，3个实例中，应力理论计算结果与实测结果变化趋势一致，其中最大相对误差为12.24%，表明运用断裂力学裂纹扩展这种微观应力分析方法来分析宏观采场推进过程中应力变化是可行的。因此，理论结果可以作为采煤工作面应力变化的真实情况来加以分析。

?

需说明两点：一是文中理论推导是在煤层埋深大于500 m条件下进行，工作面推进距离L为从开切眼开始到工作面推进一定距离时，此时采空区未被跨落的岩石填满。随着工作面不断推进，顶板出现周期性来压，这时L为采空区压实区到工作面的距离；二是理论计算未考虑采场存在大构造应力的情况，如果采场周围存在大构造且已知构造应力时，应将构造应力叠加上去计算工作面围岩应力。

4 工作面围岩破坏范围计算模型

4.1 工作面煤层破坏宽度计算

由弹性力学理论可知，主应力σ1，2为：

联合式（11）与式（12），可求得平面情况时的最大和最小应力：

假设深部煤岩体破坏服从莫尔库伦强度准则，则采场围岩处于极限应力状态时应满足：

式中，φ为岩石内摩擦角，c为岩石内聚力。将式（13）代入式（14）整理可得工作面边缘煤岩体破坏位置：

通过

可求得：

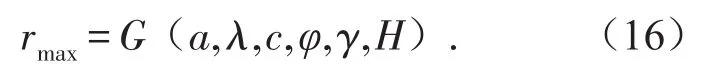
式（16）表示工作面边缘煤岩体破坏最大距离。从式（16）可知，采场围岩破坏临界位置与煤层开采宽度a、围岩力学参数以及埋深有关。式（12）～式（16）的计算比较复杂，很难得到一个简单的解析表达式，但可进行编程计算，程序见附录。通过程序计算了在相同条件下，工作面前方的破坏距离随岩石内摩擦角的变化，如图10所示。

从程序计算结果可知，随着煤岩内摩擦角增加，工作面边缘最大破坏距离减小。在不确定煤层倾角条件下进行了本次程序计算，通过程序对式（15）函数求极值。而针对具体工作面计算时，可由矿层倾角β及其力学参数确定。

当β=0°时，只考虑平面应力情况，即可得到工作面矿岩体的破坏位置：

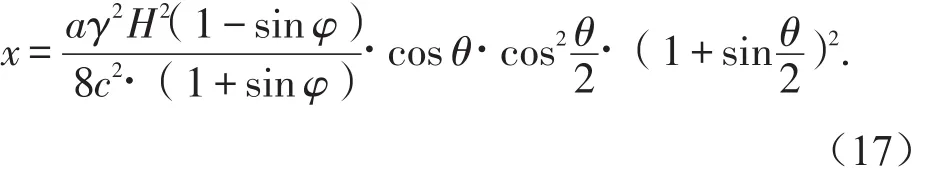
当β=0°，θ=0°时，可得到水平煤层工作面正前方煤岩体的破坏位置x0。

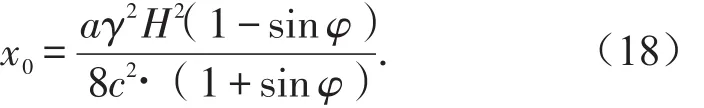
由式（18）可知，水平煤层工作面正前方围岩破坏距离与围岩力学参数成反比，与煤层开采宽度L=2a及埋深成正比。如果采空区垮落岩石压实所需时间一定，可知工作面正前方围岩破坏距离与工作面推进速度呈正相关。

4.2 工作面底板破坏深度计算

根据图11可求得工作面底板破坏深度。

在图11中，设垂直于开采煤层的破坏岩体深度AB=h，由几何关系可求得：

将式（15）代入式（18）中，整理后得：

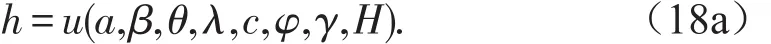
通过

可求得底板岩体的最大破坏深度，即：

式（19）即为工作面底板破坏深度的计算式，与工作面边缘煤体破坏距离的计算模型相似，由于计算公式比较复杂，可按分析工作面破坏宽度思路进行分析，此处不再赘述。

5 结论

（1）基于断裂力学理论，将任意倾角煤层深部开采的采空区剖面看作无限大岩体中一条裂纹，利用无限大薄板中裂纹周边受力分析方法对深部采场工作面围岩应力分布进行研究，得到工作面围岩应力分布规律模型，该模型可由表征应力周期变化的f（θ，β）函数和反映应力强度的K函数构成；其中f（θ，β）函数图像随θ、β呈现周期性的变化，K函数图像与离工作面距离呈双曲线变化，随采深呈线性增加；而工作面围岩应力不是线性变化而是呈波动性变化。

（2）通过围岩应力的理论计算与3个实例实测结果比较分析，最大相对误差为12.24%，应力理论计算分布与实测结果有相同的变化趋势，说明运用细观裂纹扩展的分析方法来分析深部开采的宏观采场围岩应力分布情况是可取的。

（3）将工作面围岩任意一点的应力换算成主应力代入岩石强度准则中，到任意倾角煤层回采工作面边缘煤岩体极限破坏的位置以及工作面底板破坏深度分可通过程序计算得到。

（4）水平煤层时，深部采场工作面正前方围岩破坏距离与围岩力学参数成反比，与煤层开采宽度及埋深成正比。

［1］ 李俊平，王红星，王晓光，等.卸压开采研究进展［J］.岩土力学，2014，35（S2）:350-358.Li Junping，Wang Hongxing，Wang Xiaoguang，et al.Research progress in pressure-relief mining［J］.Rock and Soil Mechanics，2014，35（S2）:350-358.

［2］ 刘万荣，彭 超，李传明，等.深埋隧洞围岩稳定性分析［J］.中国安全科学学报，2015，25（5）:120-125.Liu Wanrong，Peng Chao，Li Chuanming，et al.Stability analysis of surrounding rock of deep underground tunnel［J］.China Safety Science Journal，2015，25（5）:120-125.

［3］ 耿 琳.深部采场采空区基本顶来压规律研究［D］.阜新:辽宁工程技术大学，2011.Gen Lin.Mine Pressure Rule of Basic Roof in Deep Mining［D］.Fuxing:Liaoning Technical University，2011.

［4］ 刘书贤，魏晓刚，王 伟，等.深部采动覆岩破断的力学模型及沉陷致灾分析［J］.中国安全科学学报，2013，23（12）:71-77.Liu Shuxian，Wei Xiaogang，Wang Wei et al.Mechanical model of overlying strata rupture caused by deep coal mining and analysis of strata subsidence disaster［J］.China Safety Science Journal，2013，23（12）:71-77.

［5］ 宋艳芳，唐 治，潘一山，等.孤岛工作面应力分布规律的数值分析［J］.中国地质灾害与防治学报，2012，23（4）:65-68.Song Yanfang，Tang Zhi，Pan Yishan，et al.Numerical analysis of stress distribution of isolated working face in undergrourd mining area［J］.The Chinese Journal of Geological Hazard and Control，2012，23（4）:65-68.

［6］ 史 红，姜福兴.基于微地震监测的覆岩多层空间结构倾向支承压力研究［J］.岩石力学与工程学报，2008，27（S1）:3274-3280.Shi Hong，Jiang Fuxing.Study on abutment pressure rule of overlying strata spatial structures based on microseismic monitoring［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（S1）:3274-3280.

［7］ 刘金海，姜福兴，王乃国，等.深井特厚煤层综放工作面支承压力分布深井特厚煤层综放工作面支承压力分布［J］.煤炭学报，2011，36（S1）:18-22.Liu Jinhai，Jiang Fuxing，Wang Naiguo，et al.Survey on abutment pressure distribution of fully mechanized caving face in extra-thick coal seam of deep shaft［J］.Journal of China Coal Society，2011，36（S1）:18-22.

［8］ 唐军华，白海波，杜 峰.采场支承压力分区变异特征研究［J］.采矿与安全工程学报，2011，28（2）:293-297.Tang Junhua，Bai Haibo，Du Feng.Character of the zonal variation of abutment pressure in working faces［J］.Journal of Mining&Safety Engineering，2011，28（2）:293-297.

［9］ 周 钢，李玉寿，张 强，等.陈四楼矿综采工作面采场应力监测及演化规律研究［J］.煤炭学报，2016，41（5）:1087-1092.Zhou Gang，Li Yushou，Zhang Qiang，et al.Research on monitoring technique and evolution law of the disturbance stress in Chensilou Colliery［J］.Journal of China Coal Society，2016，41（5）:1087-1092.

［10］程家国，曲 华.深井高地压坚硬顶板采场围岩特性的数值模拟［J］.采矿与安全工程学报，2006，23（1）:70-73.Cheng Jiaguo，Qu Hua.Numerical simulation of characteristics of surrounding rock in working faces with strong roof and high ground pressure in deep mines［J］.Journal of Mining&Safety Engineering，2006，23（1）:70-73.

［11］刘 杰，王恩元，赵恩来，等.深部工作面采动应力场分布变化规律实测研究［J］.采矿与安全工程学报，2014，31（1）:60-66.Liu Jie，Wang Enyuan，Zhao Enlai，et al.Distribution and variation of mining-induced stress field in deep work face［J］.Journal of Mining&Safety Engineering，2014，31（1）:60-66.

［12］Chaoru Liu.Distribution laws of in-situ stress in deep underground coal mines［J］.Procedia Engineering，2011，26:909-917.

［13］胡建华，习智琴，周科平.深部采空区尺寸效应的危险度正态云辨识模型［J］.中国安全科学学报，2016，26（10）:70-75.Hu Jianhua，Xi Zhiqin，Zhou Keping.Normal cloud model for identifying hazard degree ofdeep goaf size effect［J］.China Safety Science Journal，2016，26（10）:70-75.

［14］叶义成，施耀斌，王其虎，等.缓倾斜多层矿床充填法开采围岩变形及回采顺序试验研究［J］.采矿与安全工程学报，2015，32（3）:407-413.Ye Yicheng，Shi Yaobin，Wang Qihu，et al.Experimental study of deformation of wall rock and stoping sequence in mining gently inclined and multilayer deposits by backfill mining［J］.Journal of Mining&Safety Engineering，2015，32（3）:407-413.

［15］罗斌玉，叶义成，胡南燕，等.基于应变能平衡的条带矿柱破裂宽度及其影响因素［J］.金属矿山，2016（8）:48-52.Luo Binyu，Ye Yicheng，Hu Nanyan，et al.Width of fractured zone of strip pillars based on the strain energy balance theory and its influencing factors［J］.Metal Mine，2016（8）:48-52.

［16］王其虎.地下开采中接触带复合岩体非协调变形及控制研究［D］.武汉，武汉科技大学，2015.Wang Qihu.Study on Contact Zone Composite Rock Mass Incompatible Deformation and Control in Underground Mining［D］.Wuhan:Wuhan University of Science and Technology，2015.

［17］李世愚，和泰名，尹祥础.岩石断裂力学导论［M］.合肥:中国科学技术大学出版社，2010:144-156.Li Shiyu，He Taiming，Yin Xiangchu.Introduction of Rock Francture Mechanics［M］.Hefei:University of Science&Technology of China Press，2010:144-156.

［18］张金才，张玉卓，刘天泉.岩体渗流与煤层底板突水［M］.北京:地质出版社，1997:24-27.Zhang Jincai，Zhang Yuzhuo，Liu Tianquan.Rock Mass Seepage and Water Inrush from Coal Floor［M］.Beijing:Geological Publishing House，1997:24-27.

［19］郑 军.大倾角厚煤层放顶煤开采覆岩运动规律与矿压特征研究［D］.焦作:河南理工大学，2011.Zheng Jun.Study on Movement Laws of Overlying Rock and Strata Feature of Top-caving，Mining in Illclilled Thick Coal Seam［D］.Jiaozuo:Henan Polytechnic University，2011.

［20］夏永学.屯留矿大采高综放工作面矿压显现规律与煤壁稳定性研究［D］.北京:煤炭科学研究总院，2008.Xia Yongxue.Study on the Laws of Strata-Pressure Behavior and the Stability of the Coal wall in Large Mining Height and Top Coal Caving Working face in Tunliu Mine［D］.Beijing:Coal Science Research Institute，2008.