基于迭代反馈整定的车辆横向控制系统研究
2018-07-10朱立宗牛彩云曾清德邓剑锋张彦会
朱立宗, 牛彩云, 曾清德, 邓剑锋, 张彦会
(1. 广西科技大学 职业技术教育学院, 广西 柳州 545006;2. 广西生态工程职业技术学院 汽车与信息工程系, 广西 柳州 545003)
0 引 言
当前汽车智能化水平已经成为人们关注的焦点, 而横向控制作为实现车辆智能控制的关键组成部分, 对促进车辆的智能化发展具有重要的意义. 横向控制, 即车辆的转向控制, 其控制性能的好坏直接决定着车辆行驶过程的舒适度和平稳性. 文献[1]从人工势场出发, 基于李亚普诺夫的控制方法较好地完成了车辆的弯道轨迹跟踪效果; 王家恩等人[2]采用滑模控制方法通过跟踪期望横摆角速度实现车辆的横向控制, 而李林辉等人[3]则将滑模控制和模糊控制方法进行融合, 设计了智能车辆横向控制策略, 从而保证参考路径的准确和稳定跟踪; 在文献[4]中, 作者针对车辆横向稳定性控制中的非线性问题, 提出了一种基于预测控制的车辆横向稳定性控制方法. 此外, 也有从自适应控制[5]、 H∞控制[6]、 基于代理模型理论的优化策略[7]、 虚拟控制律[8]等角度对车辆的横向控制问题进行的研究. 上述方法从不同角度针对不同的横向控制要求和目标提出了行之有效的解决途径. 但车辆在运动过程中, 由于受路况、 环境、 车辆运动状态和载荷等变化因素的影响和作用, 建立车辆运动过程中的精确动力学模型将变得非常困难, 使得上述基于模型的控制方法难以适应变化因素的影响, 无法满足更高要求的控制和目标跟踪.
相比基于模型的控制方法, 基于数据驱动的控制方法, 只需根据系统的离线或在线I/O数据以及经过数据处理而得来的知识即可完成控制器的设计过程, 而不需要系统的任何模型信息, 其在理论和应用方面都获得了长足发展. 目前, 数据驱动控制方法包括PID、 迭代反馈整定(Iterative Feedback Tuning, IFT)[9-10]、 虚拟参考反馈整定(Virtual Reference Feedback Tuning, VRFT)[11-12]、 无模型自适应控制(Model Free Adaptive Control, MFAC)[13]、 同步扰动随机逼近(Simultaneous Perturbation Stochastic Approximation, SPSA)[14-15]、 模糊控制[16-18]等. 其中, PID方法由于控制器结构简单, 计算快捷, 工业应用较为广泛, 但其参数的整定需要依靠一定的先验知识和人工整定过程, 且随着系统的复杂化和环境因素变化的影响, 整定过程越发变得困难. 而IFT方法通过获取闭环实验数据采用随机优化的方法便可完成控制器参数的自整定过程, 对人工先验知识要求低, 因此得到大量应用[19-20].
虽然IFT方法在很多领域已取得成功应用, 但到目前为止, 并未见IFT方法在车辆横向控制中应用研究的报道, 因此, 本文基于IFT方法研究车辆的横向控制系统的设计和实现过程, 以期为车辆的横向控制研究提供一定的借鉴和技术支撑.
1 车辆横向控制系统设计
1.1 控制目标最小化
假设移动车辆的离散时间系统模型为
y(k)=Pu(k)+v(k),
(1)
式中:y(k)为移动车辆的输出;u(k)为移动车辆的控制输入;v(k)为干扰信号, 这里设为零均值的扰动信号;P为移动车辆的数学模型;k为采样离散时间. 给定如下参数未知而结构已知的控制器
u(k)=C(θ,z-1)e(k),
(2)
式中:C(θ,z-1)是控制器关于参数向量θ的传递函数,θ∈Rnp为np维实数向量;z-1为时间向后一步移位的算子, 即z-1y(k)=y(k-1);e(k)=r(k)-y(k) 是输出误差. 式(1), 式(2)组成如图 1 所示的车辆闭环控制系统框图.

图 1 车辆闭环控制系统Fig.1 Closed-loop control of one vehicle
为表达简便, 记y(θ),u(θ)分别为控制器(2)作用于车辆之后闭环系统的控制输出和输入信号. 控制目标为使控制输出误差信号关于控制器参数的某种范数达到最小, 并通过整定控制器参数向量θ实现其最小化. 本文选用如下普遍认可的二次型性能指标函数
(3)
式中:N为移动车辆运行过程的采样截止时刻;E[·]指关于噪声的期望值;λ为控制输入权重因子. 二次性能指标的最小过程为:
式(3)两边对θ分别求偏导并令其等于零, 得

(4)
由式(4), 利用如下递归搜索算法完成下一次迭代控制参数的计算
(5)
式中:Ri为Hessian矩阵;γi为迭代步长因子, 是一个正的实数标量.
在式(5)中, 当前迭代输出误差信号和控制输入信号都可直接获取, 而相应的两项一阶导数则未知, 为获取该两项一阶导数, 需借助一定的梯度试验进行推导.
1.2 系统输出误差的一阶偏导估计
结合式(1)和式(2), 得移动车辆输出误差相对控制器参数向量θ的一阶偏导为

(6)

结合式(1), 式(2)和图 1, 将式(6)改写为
(7)
为计算出表达式(7), 设计如下连续两次闭环试验
(8)

将式(8)代入式(7)并整理, 且根据扰动信号的零均值假设, 可获得如下所示输出误差信号的一阶偏导的无偏估计
(9)

1.3 控制输入的一阶偏导估计
为计算控制输入的一阶偏导, 需求取控制输入的闭环输出表达式, 将式(1)代入式(2), 可得控制输入的闭环形式
u(θ)=S0(θ)C(θ)[r-v],
(10)
则得控制输入相对参数向量θ的一阶偏导
(11)
根据式(8)的两次闭环试验, 可将其转化为如下有关控制输入的表达式
(12)
(13)
此外, 根据式(9)和式(13), Hessian矩阵的估计值可采用如下形式

(14)
1.4 车辆横向控制方案
根据以上关于移动车辆闭环控制系统的设计过程, 可总结基于IFT方法的移动车辆横向控制系统实现的步骤:
1) 给定结构已知而参数未知的控制器C(θ), 初始化控制器参数向量θ, 并施加给移动车辆;
2) 根据如下两次闭环试验
获取所需输出信号y1(θi)和y2(θi);
3) 根据
5) 换向。当车钟手柄从非海上全速正车位置直接扳到倒车任意位置时,主机转速下降到制动转速,输出停车指令控制主机停机,待主机停机之后反向启动主机。
获得所需输入信号u1(θi)和u2(θi);
4) 根据y1(θi),y2(θi)和u1(θi),u2(θi), 计算
5) 根据2)~4)计算结果, 计算
e1(θi)=r-y1(θi),
6) 更新控制器参数向量
并作用于移动车辆, 令i=i+1, 返回到2).
2 仿真分析
为验证所采用IFT方法对车辆横向控制的有效性, 本文选择经典的PID方法作为仿真对比, 并设计了一种直线-弯道-直线轨道的仿真工况, 该工况为: 车辆首先沿x轴方向直线行驶50 m, 再进入弯道半径为200 m的左弯道上行驶90°, 最后沿y轴方向直线行驶50 m.
为保证公平对比,在车辆的横向控制过程中, IFT和PID方法的初始条件设置相同.
参考文献[16], 选用如下形式的车辆运动学模型

(15)
式中:v=6.25 m/s为车辆纵向轴方向的速度; Δt=0.16 s 为采样时间间隔;θ为车辆纵向轴方向与x轴方向的夹角, 即横向偏角;α为车辆前轮参考本身纵向轴方向的控制转向角度;l=1.5 m为车辆轴距.
由此可知,α即为车辆的横向控制输入变量u,θ为车辆的横向控制输出角度变量y. 需要指出的是, 采用的IFT方法不需要利用任何有关运动学模型(15)的模型信息, 该模型只用于产生I/O数据.
本文选用的PID控制器结构为
u(k)=
其中,KP,TI和TD分别指PID控制器的增益、 积分和微分常数.
图 2 和图 3 分别为IFT和PID两种控制方法的车辆横向偏角跟踪性能, 图 4 和图 5 则为两种控制方法在所设计的直线-弯道-直线目标的运动跟踪性能. 在跟踪所设定的直线-弯道-直线目标轨迹情况下, IFT和PID两种方法经计算产生的最大相对误差分别为: 1.02%和1.69%, 说明这两种方法都达到了良好的控制效果. 以下将从控制舒适度和控制精度两方面具体分析这两种方法的控制效果.

图 2 基于IFT的车辆横向偏角跟踪性能Fig.2 Tracking performance of the lateral angle based on IFT

图 3 基于PID的车辆横向偏角跟踪性能Fig.3 Tracking performance of the lateral angle based on PID
为具体比较图 2 和图 3 两种控制方法所获得的驾驶舒适度, 选取横向偏角跟踪最大绝对误差(用MAE表示)和绝对误差变化积分(用IVAE)进行评价. 由表 1 可看出, 关于车辆的横向偏角跟踪性能, 经过整定后的IFT方法, 所获得MAE比PID的小0.009 9 rad, 说明其控制的横向偏角变化更为平滑, 而获得的IVAE比PID的小0.210 0 rad, 说明跟踪目标横向偏角的变化过程更为平稳. 由此可见, 较PID方法, 采用IFT方法能够获得更好的驾驶舒适度.
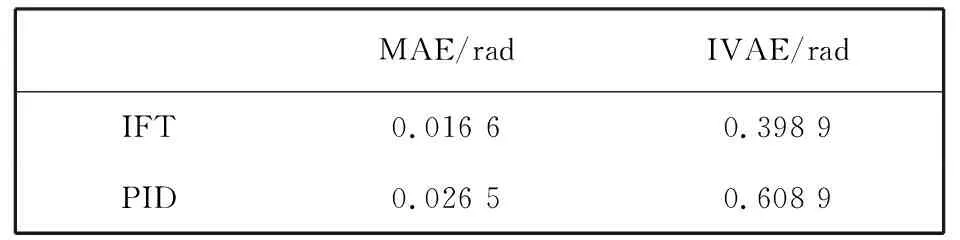
表 1 舒适度评价Tab.1 Evaluation of comfort
IFT的控制器结构为
为了比较图 4 和图 5 两种控制方法的具体轨迹跟踪效果, 本文选取横向偏差的均方误差(用MSE表示)和式(3)所示的性能指标函数(用JP表示)作为评价准则. 其中, 控制输入权重因子选取为λ=10, 该权重因子的选取主要用于保证控制输入变化不至于过快, 同时避免控制过程输出信号出现较大波动.

图 4 基于IFT的车辆运动轨迹跟踪性能Fig.4 Tracking performance of the motion trail based on IFT

图 5 基于PID的车辆运动轨迹跟踪性能Fig.5 Tracking performance of the motion trail based on PID
根据表 2 可以看出, IFT方法获得的JP值比PID方法的小0.41×10-4, 获得的MSE值比PID方法的小2.74×10-4rad2, 这说明了IFT方法比PID方法能够获得更小的控制均方误差和控制性能指标函数, 控制精度更高. 此外, 在控制器参数的整定过程中, 采用IFT方法避免了人工整定控制器参数过程带来的耗时和困难性. 由此说明了IFT方法在车辆横向控制过程中的有效性.

表 2 评价准则Tab.2 Evaluation criterion
3 结 论
本文基于IFT方法对车辆的横向控制进行了仿真研究, 通过构建车辆的横向控制系统, 对车辆在直线-弯道-直线目标轨迹工况下进行了实验, 并与传统PID方法进行了对比仿真, 仿真结果表明, 采用IFT方法在设计的实验中, 跟踪的横向偏角最大绝对误差比PID的小0.009 9 rad, 绝对误差变化积分小0.210 0 rad, 即能够获得更好的驾驶舒适度; 而跟踪的性能指标函数比PID的小0.41×10-4, 跟踪的均方误差比PID的小2.74×10-4rad2, 即控制精度更高.
