多自由度参数振动混沌控制方法研究*

黄迪山 刘献之 邵何锡

(上海大学机电工程与自动化学院, 上海 200072)

引言

随着对混沌运动的发现与研究,人们已经认识到大多数系统都可能转化为混沌运动,近十年来,混沌控制的领域也有了较多的发展,相继提出了参数微扰动控制法、自适应控制法、神经网络法等控制方法.对具有时变参数的参数振动的主动控制也一直是个棘手的问题,对此sinha提出了Liapunov-Floquet变换[1]理论,将时变系统转化为时不变系统,再通过引入状态反馈,配置系统闭环极点完成对该参数振动系统的主动控制[2].

本文将通过分析直升机旋翼的动力学模型即耦合倒立双摆模型,使用L-F变换,结合极点配置,对多自由度参数振动做主动控制研究.同时,绘制相轨迹与庞加莱映射图,分析主动控制对系统混沌的抑制情况.

1 振动模型

直升机在前行时,其旋翼叶片会受到时变的载荷力及力矩,进而引起参数振动.学者sinha针对上述动力学问题,建立了如下图1所示的耦合倒立双摆系统模型,其中双摆和固定基础之间通过弹性系数为kt1和kt2的扭弹簧连接,双摆杆中间位置由弹性系数为k的弹簧链接而耦合,而且摆杆摆动时,存在阻尼系数为c1和c2,摆杆顶部存在两个集中质量m,分别受到时变载荷P1cosωt和P2cosωt,摆杆自身受到变力矩Pu1cos(ωpt)、Pu2cos(ωpt)的外激励作用.

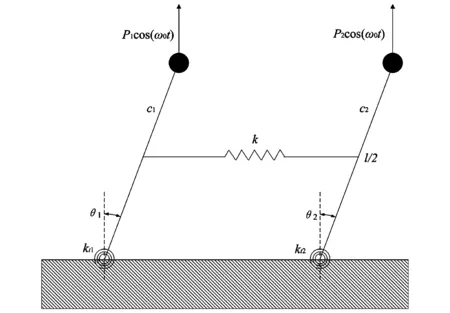
图1 振动系统框图Fig.1 Vibration system

基于上述模型,建立系统参数振动运动方程如下：(考虑了扰动情况,增加高次项)

(1)

(2)

为了对该直升机旋翼模型做振动主动控制,必须将该模型进行线性化处理,并且使用极点配置,完成系统稳定性分析.

当处于平衡位置,即X=0时,对非线性项使用泰勒级数展开进行线性化,可以得到线性化后的状态空间表达式：

(3)

其中M是n×n惯性阵,C、K、B是n×n阶实矩阵,P是n×1列向量.

将上述状态方程写成如下形式：

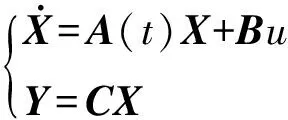
(4)

(5)

2 Liapunov-Floquet变换

Liapunov-Floquet变换[3]主要将时变系统[4]转化为时不变系统,周期为T的Liapunov-Floquet变换(L-F变换)过程如下：

若系统状态方程如下：

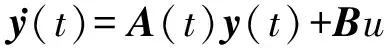
(6)

其中y(t)是n维向量,A(t)是周期为T的n×n阶实矩阵.

则上式的状态转移矩阵Φ(t)可以写成如下:

Φ(t)=Q(t)eRt,Q(t)=Q(t+2T),Q(0)=I

(7)

Q(t)是周期为2T的实数矩阵,且Q(t)是L-F转换矩阵,R为n×n阶时不变矩阵,I是单位矩阵.

将y(t)=Q(t)z(t),带入上式,变化为时不变系统,得到如下表达式：

(8)

根据上式(7),当t=2T时：

(9)

同理,根据(7),可以得到：

Q(t)=Φ(t)e-Rt

(10)

因此,要得到与原时变系统等价的时不变系统,必须要知道常系数矩阵R和状态转移矩阵Φ(t).利用Neumann[5]级数,可以求出上述的状态转移矩阵Φ(t).

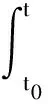
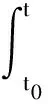
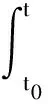
(11)

式中τ0,τ1为无实际物理含义的中间积分变量,对于系统(4)而言,其积分下限为t0=0,积分上限为时间变量t,该过程可以通过Matlab的符合运算[6]工具求解得到.

Φ11=-5.4907sin(3t)-0.14466sin(6t)-

78.953sin2(1.5t)-1.9288sin2(3t)+

2.3146tcos(3t)+66.663tsin(3t)+

4.9997t3cos(3t)+15.026t-35.484t2-

6.451t3+53.875t4-6.473t5-4.9997t2sin(3t)+

99.994t2sin2(1.5t)+1

(12a)

Φ12=0.059097sin(3t)-(2.7327e-6)sin(6t)+

1.2341sin2(1.5t)-(3.858e-5)sin2(3t)+

(5.4012e-5)cos(3t)-0.92541tsin(3t)-

0.069412t3cos(3t)-0.17733t+0.24975t2+

0.10225t3-1.269t4+0.14718t5+

0.069418t2sin(3t)-1.3881t2sin2(1.5t)

(12b)

Φ44=3.445sin(3t)-0.12057sin(6t)+

82.68sin2(1.5t)-9.6455sin2(3t)-

(6.1698e-8)cos(3t)+0.48227tcos(6t)-

66.205tsin(3t)-2.8936t3cos(3t)-11.791t-

30.344t2+10.754t3+25.857t4-3.8949t5+

6.8289t2sin(3t)+0.72341t2sin(6t)+

34.636t3sin(3t)-4.3349t4sin(3t)-

69.446t2sin2(1.5t)+23.150tsin(3t)sin2(1.5t)+1

(12c)

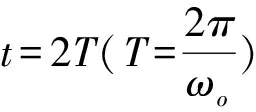
(13)

将式(13)代入式(9)就可以得到L-F变换后的时不变系统的系统矩阵R：

(14)

于是原系统可线性化为：

(15)

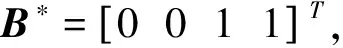
3 极点配置

闭环系统的极点分布情况,直接决定了系统的稳定性和动态品质.在系统设计过程中,通常根据系统的品质要求规定闭环系统的极点分布情况,再通过选择合适的反馈增益矩阵,使给定系统的闭环极点恰好处于复平面上所期望的位置,此过程即状态反馈系统的极点配置[7].

首先考虑系统能控性,rank[BABA2BA3B]=4,由于系统矩阵满秩,该控制系统完全可控.因此对于系统(15)的状态空间表达式,引入状态反馈控制律：

u=-Kz+v

(16)

K为状态反馈矩阵,v为输入,闭环控制系统的状态空间表达式为：

(17)

其系统框图如图2所示,是典型的状态负反馈闭环系统.

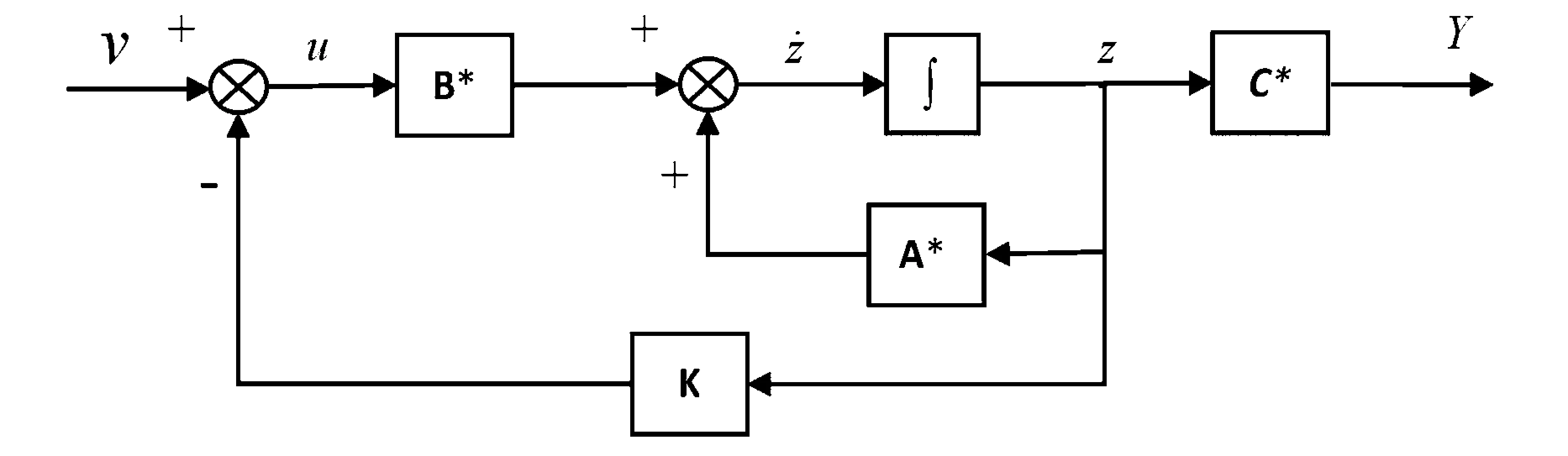
图2 状态负反馈系统框图Fig.2 Negative state feedback system

针对耦合倒立双摆模型,实际的控制系统框图如图3所示.

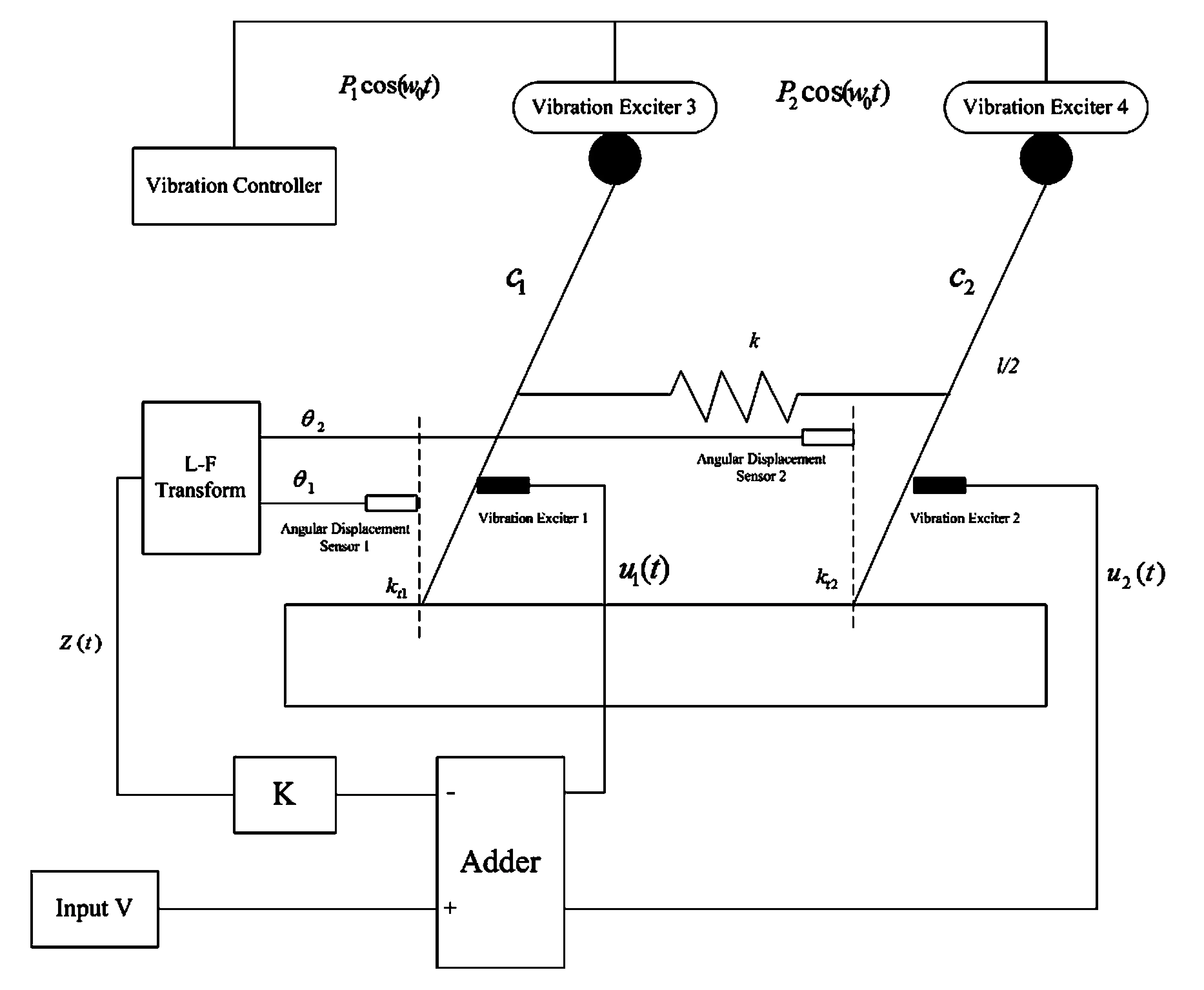
图3 振动控制系统框图Fig.3 Vibration control system

考虑原先给定的系统(15)的极点分布情况,根据前文给定的参数,系统线性化后的状态方程：

(18)

可以求得开环系统的极点为2.6898±0.3570j, 2.4558±0.3462j, 如下图4所示,系统极点分布于复平面的右半平面,系统在激励的作用下将产生增幅正弦振荡现象[8].如果希望系统响应稳定,那么就要将系统的极点配置到复平面的左半面[9],并且位置不能靠近单位圆.

假设给定要求：对系统设计状态反馈使得系统闭环阶跃响应的超调量σ小于5%,且在稳态误差值Δ为1%范围内的调节时间ts小于1s.则可以采用主导极点法进行状态反馈极点配置.

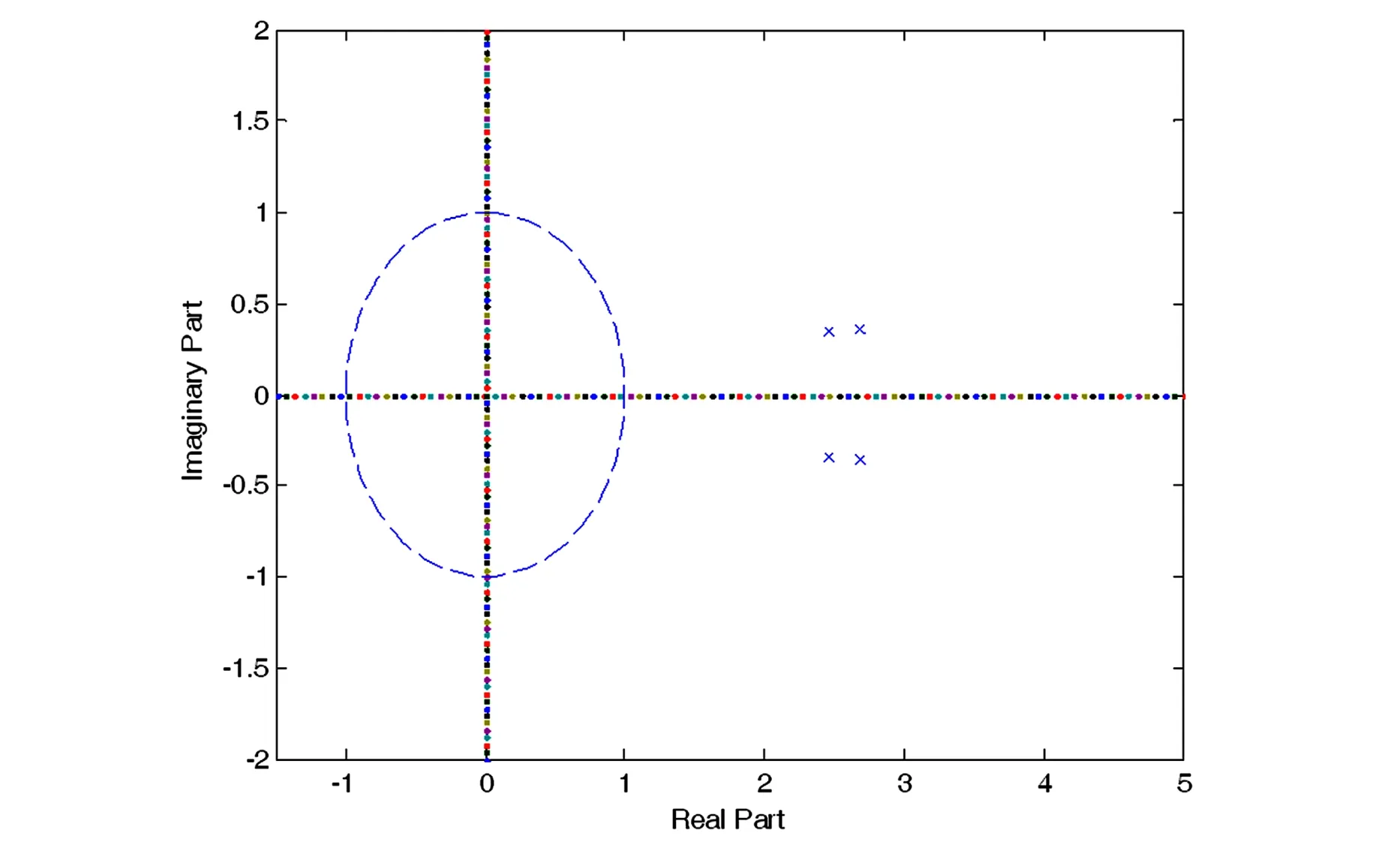
图4 极点配置前零极点图Fig.4 Zero-pole graph before using pole assignment

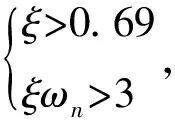
(s2+6.4s+16)(s+12)(s+15)

(19)

求得状态反馈矩阵K：

K=105[4.9196 2.0019 -1.5585 1.5589]

(20)

极点配置后系统的极点分布情况如图5所示,可以发现极点已经全部移至系统复平面的左半平面,因此系统达到镇定.

图5 极点配置后零极点图Fig.5 Zero-pole graph after using pole assignment

原系统的单位脉冲响应如图6,可见原系统的单位脉冲响应随着时间变化逐渐趋近于无穷大,系统处于不稳定状态.通过极点配置后,单位脉冲响应图如图7,对于输出z(t),系统响应时间大概为1s,且随时间增大逐渐趋近于0,说明系统在很短时间达到稳定,满足配置要求.

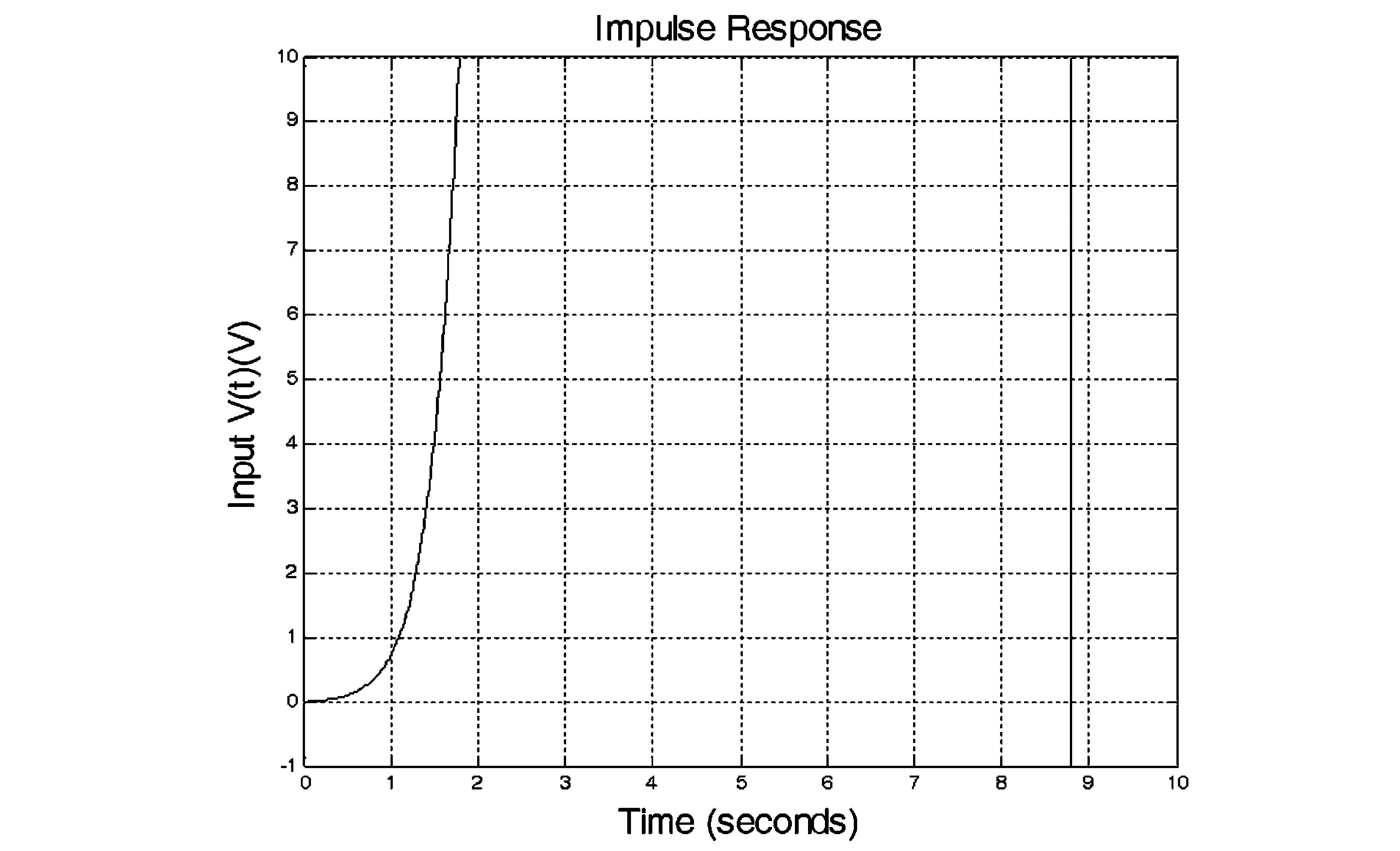
图6 极点配置前单位脉冲响应图Fig.6 Unit impulse response before using pole assignment

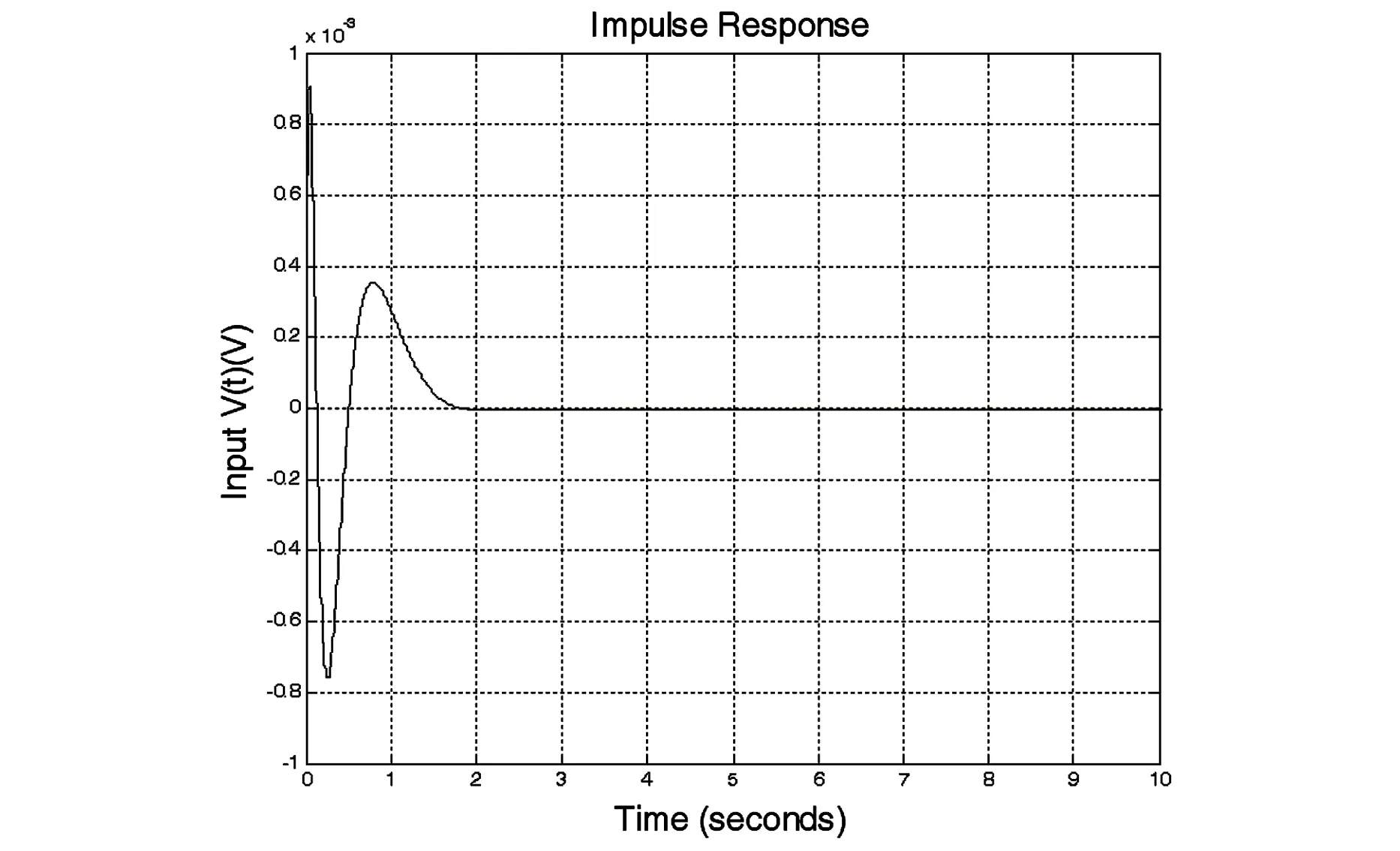
图7 极点配置后单位脉冲响应图Fig.7 Unit impulse response after using pole assignment

工程应用中,系统的激励一般为窄带随机信号,使用图8的窄带随机信号作为输入信号.

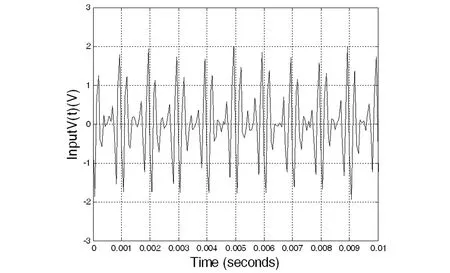
图8 系统输入信号图Fig.8 Input signal

极点配置后,系统在该激励信号下的响应如图9所示.

图9 随机响应图Fig.9 Random response

4 参数振动混沌

混沌运动[10]是一种非常普遍的非线性现象,它作为非线性动力系统的重要特征已引起了人们的广泛重视.利用系统相平面中的相轨迹图,可以对系统的混沌性态进行判定.假如系统的运动周期很长,其相轨迹将会不断延续、重叠,仅仅根据相图来判断系统的混沌振动情况有很大难度.因此,将系统的相图进行改进,即每隔一个时间间隔标出相轨迹上的一个点,将其余相轨迹点隐去,这就生成了一个点集{Pi},其中每一个点的坐标[x(iT),y(iT)],可以认为点集{Pi}是由一个映射所生成,如式所示.这样的映射被称为庞加莱映射.

Pi+1=f(Pi)

(xi+1,yi+1)=[fx(xi,yi),fy(xi,yi)]

(21)

庞加莱映射,能有效地从不断重叠的相图中提炼出系统的混沌特性,它是研究系统混沌运动的十分直观、有效的工具.

参数振动是由外界激励产生的一种振动形式,其激励是通过系统内部参数周期改变而实现.讨论参数振动问题实际上就是讨论时变系统常微分方程零解稳定性问题.本文即是针对直升机旋翼模型,即耦合倒立双摆系统,其运动方程为(1)、(2).该系统实际为非线性时变系统.本文采用基于L-F变换和极点配置的控制策略,对控制前后的参数系统绘制相轨迹图及其庞加莱映射(见图10～11),以判别该控制方法是否消除了系统的混沌特性.

控制前参数系统的相轨迹(图10(a)),在相平面中为一个永远不封闭的曲线,并且相轨迹局限在一个有界的区间内,没有发散到无穷远,这样具有极限环的相轨迹呈现典型的混沌振动特性; 由参数系统的庞加莱映射图(图10(b))可以发现,它是一个非有限点集,呈现明显的非周期特性,而且庞加莱映射中还包含有无穷嵌套的自相似几何结构,在本例中表现为瓣状轨迹,从庞加莱映射图中可以看出系统具有混沌运动的特性.

图10 主动振动前混沌情况Fig.10 Chaotic condition before active vibration

图11 主动振动后混沌情况Fig.11 Chaotic condition after active vibration

控制后参数系统的相图(图11(a)),表现为一个封闭的规则椭圆,表明系统作周期性的振动; 观察控制后的庞加莱映射图(图11(b)),庞加莱映射为有限的点集,同样说明了系统的周期振动.综上所述,参数振动系统在一定情况下会表现出其混沌振动的性态,通过采用文中基于L-F变换和极点配置的控制方法,有效地抑制了参数振动系统的非线性混沌振动.

5 小结

对于耦合倒立双摆这一多自由度参数振动系统,通过基于L-F变换、极点配置和引入反馈的控制方法,实现主动振动控制,其优点为:(1)在系统稳定的基础上,有效地抑制了参数振动系统的非线性混沌振动; (2)大大降低了控制模型以及控制策略的复杂程度,提高了控制效率.

1 Sinha S C, Pandiyan R, Bibb J S. Liapunov-Floquet transformation: computation and applications to periodic systems.JournalofVibrationandAcoustics,1996,118:209～219

2 傅晨宸,黄迪山. 参数振动主动控制系统研究. 动力学与控制学报,2014,12(3):215-5 (Fu C C, Huang D S. Study on active control for parametric vibration system.JournalofDynamicsandControl,2014,12(3):215-5 (in Chinese))

3 Bobrenkov O A, Butcher E A, Mann B P. Application of the Liapunov-Floquet transformation to differential equations with time delay and periodic coefficients.JournalofVibrationandControl,2012,19(4):521～537

4 于 霞,刘建昌,李鸿儒. 时变系统控制方法综述. 控制与决策,2011,26(9):1281～1287 (Yu X, Liu J C, Li H R. Survey on control of time-varying systems.ControlandDecision, 2011,26(9):1281～1287 (in Chinese))

5 王孝武,张晓江. 现代控制理论. 北京: 机械工业出版社, 2006 (Wang X W, Zhang X J. Modern control theory. Beijing: Mechanical Industry Publishing House,2006 (in Chinese))

6 张志涌,杨祖樱. Matlab教程R2011a. 北京: 北京航空航天大学出版社, 2011 (Zhang Z Y, Yang Z Y. Matlab Tutorial R2011a. Beijing: Beihang University Press,2011 (in Chinese))

7 张嗣瀛,高立群. 现代控制理论. 北京: 清华大学出版社, 2006 (Zhang S Y , Gao L Q. Modern control theory. Beijing: Tsinghua University Press, 2006 (in Chinese))

8 吴 宇. 系统函数H(S)的极点位置分布对系统时域特性的影响. 潍坊高等职业教育,2005,1(2):17～19 (Wu Y. System time-domain characteristics′ distribution on different pole position of system function H(S). Higher Vocational Education,2005,1(2):17～19 (in Chinese)

9 赵长德,郭美凤. 控制工程基础. 北京: 清华大学出版社, 2009 (Zhao C D, Guo M F. Foundation of control engineering. Beijing: Tsinghua University Press, 2009 (in Chinese))

10 高普云. 非线性动力学: 分叉、混沌与孤立子. 长沙:国防科技大学出版社, 2005 (Gao P Y. Nonlinear dynamics: bifurcation, chaos and soliton. Changsha:National University of Defense Technology Press, 2005 (in Chinese))