汽轮机转子碰摩热弯曲动力特性研究*

从继庆 荆建平,2,3† 陈昌敏 颜逸飞

(1.上海交通大学机械系统与振动国家重点实验室, 上海 200240)(2.上海交通大学振动噪声研究所, 上海 200240)(3.上海交通大学船舰设备噪声与振动控制技术国防重点学科实验室, 上海 200240)

引言

静转子在摩擦过程中产生的热冲击效应以及转子的干摩擦失稳是转子系统的常见故障和研究热点问题.当转子与静子接触时,转子的接触表面由于摩擦热量进入而引起表面局部温度升高,导致转子沿轴向方向产生连续的热弯曲,改变了转子不平衡量的分布,使转子的振动发生变化.对轴封与转子的摩擦温升研究表明,在摩擦较为严重的情况下,转子与轴封的温度变化会达到十分可观的程度.因此,碰摩及其热效应带来的影响不容忽视.

国内方面,朱向哲,袁惠群等人[1]采用有限元的方法,建立了以航空发动机高压转子为研究对象的考虑摩擦热效应的高压转子热碰摩动力学模型,结果表明摩擦热效应对碰摩响应的影响巨大,在实际工程问题中,不能忽略碰摩热效应的影响；张楠,刘占生等人[2]建立了高速碰摩故障转子轴承系统的非线性动力学模型,得出了滑动轴承支撑下的碰摩转子系统的振动特征；田永伟和杨建刚[3]运用特征值分析的方法,针对建立的热弯曲/振动耦合模型,研究了转速、刚度等因素对摩擦稳定性的影响；黄葆华,杨建刚[4]等建立了发生摩擦热弯曲的转子轴承系统的传递矩阵,分析了摩擦热弯曲对转子稳定性的影响；王士敏等人[5]建立了转子和静子之间的弹性接触、摩擦和热传导的简化模型,分析了转子在通过临界转速时的碰摩过程；梁明轩,袁惠群等人[6]考虑非线性滚动轴承力、不平衡量、碰摩故障及陀螺效应,建立了滚动轴承-柔性对称碰摩转子系统非线性集中质量模型,研究了系统参数变化对转子动力响应的影响.国外方面,Goldman和Muszynska[7]建立了考虑热效应影响的旋转机械转静碰摩的简化模型；Kellenberger[8]基于转子热弯曲正比于进入转子的热量,分析了因为碰摩导致的热变形随时间变化的规律；基于Kellenberger的模型,Childs[9]把间隙对轴振动影响考虑到了模型当中；Robert等人[10,11]分析了转子和密封之间的轻微碰摩问题,并计算了转子内部的三维温度分布；Chen等人[12]分析了柔性转子轴承系统中碰摩发生时系统的响应情况.目前,对于碰摩力作用的转子系统非线性碰摩响应的研究非常广泛,而摩擦热现象对复杂转子系统振动影响的研究较少[1].

1 静转子碰摩热弯曲模型

本文关于摩擦热碰摩响应是指转子系统在不平衡力、碰摩力和碰摩热弯矩耦合作用下的动力响应.图1所示为摩擦热弯曲响应数值模型,该转子系统为刚性支承,无质量弹性轴长2.7m,轴段外径0.2m,内径为0,圆盘2的质量为9164kg,m1、m2距左右两端同为0.9m,在m1处发生碰摩.

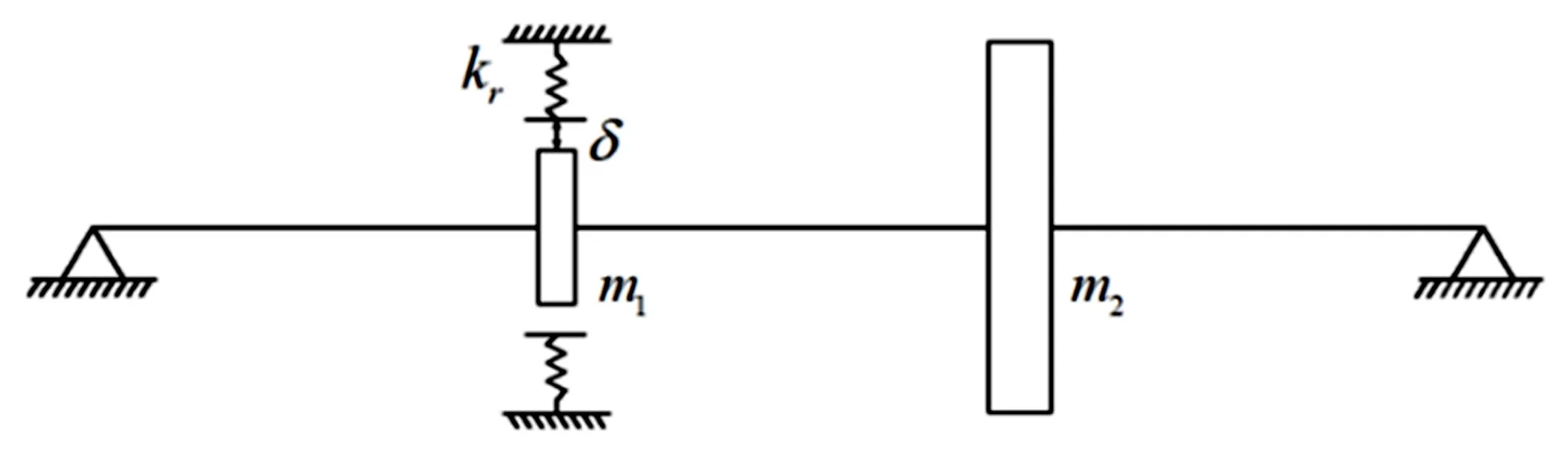
图1 转子系统动力学模型Fig.1 Dynamic model of rotor system

1.1 碰摩力模型

转子与静子的径向碰摩力模型[2]如图2所示,其中,Pr为径向碰摩力,Pt为切向摩擦力,φ为接触点的向径与x轴的夹角,Ω为转子转动角速度,e为转子偏心距.

转子与静子间的径向碰摩力采用线性当量弹簧模型,切向摩擦力采用库伦摩擦力模型,则当r>δ时,径向碰摩力、摩擦力分别为：

(1)

图2 转子与静子的径向碰摩力模型Fig.2 Radial rubbing force model of static stator and rotor

碰摩力为：

(2)

则有：

(3)

1.2 碰摩截面热分布计算

摩擦发生后,从振动高点处进入转子的热量[3]为：

q=μΩRkr(r-δ)

(4)

在计算转子和静子摩擦生热温度场时,采用以下假设：(1)不考虑摩擦过程中材料的磨损；(2)转子和静子材料满足各向同性；(3)忽略由于温度变化引起的转子物性参数的变化；(4)不考虑热量沿轴向的传播.

由传热学基本理论可知,转子碰摩截面的非稳态热传导方程为：

(5)

式中,K为热传导系数,ρ为材料密度,C为材料比热容,T为温度变量,t为时间.

由热平衡基本原理可知,热单元内的热量传递满足如下条件：

(6)

式中,H为热传导系数,Tf为外界环境温度.

在摩擦点表面,摩擦生热温度场分布可由下式确定：

(7)

忽略轴向导热,对具有对流换热及热量流入边界条件的二维瞬态热传导方程求解表明,摩擦表面任一点的温升按时间呈指数形式增长[4],故本文应用有限元软件ABAQUS模拟转轴(r=0.2m)接受碰摩热流作用和换热条件时的温度场分布,并依据碰摩表面温升的特点得到转子截面温度场的分布解析式,以便于以后的动力求解.转子材料的计算参数为：ρ=7767kg/m3,E=2.1×1011Pa,C=465J/(kg·℃),K=45W/(m·℃),γ0=1.2×10-5m/(m·℃),H=265W/(m2·℃).

所得转子截面温度场如图3所示.在ABAQUS热分析中,通过设置碰摩监测点,在历史变量的输出中得到碰摩点温度随输入的恒定热流的变化关系,如图4所示.

图3 转子截面温度场分布Fig.3 Temperature distribution in the rotor section

图4 碰摩点温度变化曲线Fig.4 Temperature variation curve of the rubbing point

应用MATLAB对以上碰摩点的温度变化曲线进行多项式拟合,所得结果为：

Tp=αnqn+αn-1qn-1+…+α1q+α0

(8)

1.3 热弯矩计算

对于转子系统的热应力分布,可以简化为作用于转子系统的等效热弯矩,该等效弯矩可以产生相似的热应力应变分布和热变形.则等效热弯矩Mx、My可按下式计算：

(9)

图5 温度的径向变化及拟合曲线Fig.5 Temperature radial variation curve and its fitting curve

图6 温度线性化示意图Fig.6 Linear temperature diagram

式中γ0是材料线性膨胀系数,E是材料弹性模量,A是摩擦截面面积,Ti(x,y)是摩擦截面坐标(x,y)处的温度值.

针对本文模型有：

(10)

2 转子系统运动方程

(11)

式(11)为采用柔度影响系数的方法建立的具有N个圆盘转子系统的运动微分方程式[13],这是一组由4N个二阶线性微分方程构成的方程组.其中[M]是质量矩阵,[K]是刚度矩阵,[G]是回转矩阵.

依据式(11)建立本文转子系统的运动微分方程,设圆盘的质量、直径转动惯量、极转动惯量和内阻尼系数分别为mi、Jdi、Jpi和ci(i=1,2)转子轴长为l,抗弯刚度为EI,则可得系统的运动微分方程为：

(12)

其中：

{u1}=[x1,θy1,x2,θy2]T

{u2}=[y1,-θx1,y2,-θx2]T

由梁的弯曲变形公式及柔度系数法可得系统的柔度及刚度矩阵：

考虑实际系统所受的不平衡力、碰摩力及热弯矩作用,则得到运动微分方程为：

(13)

为便于MATLAB数值求解,需对以上微分方程组进行无量纲化处理,无量纲后的运动方程为(本模型从简,令m1,Jd1,Jp1,c1=0)：

(14)

式中：

对此方程中的四个线性方程进行变量求解后代入微分方程,整理后的微分方程组为：

(15)

3 转子系统动力学分析

本文针对转子低于临界转速、接近临界转速和高于临界转速时的转子碰摩热弯曲现象,对转子动力学特性进行了分析,其转子响应与温度场联合求解的流程如图7所示.

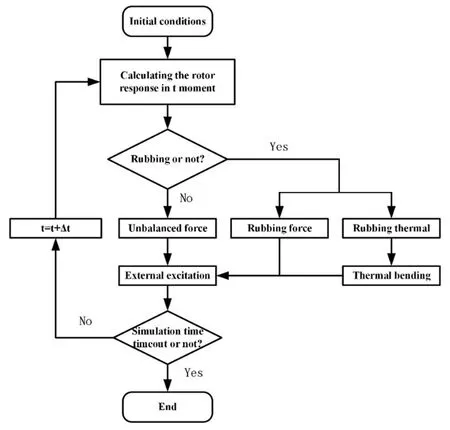
图7 计算求解流程图Fig.7 Flow chart to solve the rotor response and temperature field

由于系统具有很强的非线性,非线性系统的周期解有很多方法,但数值方法仍然是研究系统拟周期现象最有效的工具,本文利用四阶Runge-Kutta方法求解微分方程组获取转子系统的响应,计算的初始条件全选为0,数值仿真无量纲时间步长取π/200,收敛偏差标准取为10-6.因仿真在圆盘1处发生碰摩,此处的振动特征最为显著,故主要研究圆盘1处的振动特征(模型固有频率42Hz).

3.1 低于临界转速时的摩擦振动

图8所示为转子低于临界转速运行时发生碰摩的仿真结果.由图可见,考虑热弹性效应的转子在长时间输入碰摩热流的作用下振动由平稳状态逐渐发散,此时的1X幅值大幅增加,并出现了2X和3X等高频成分；碰摩力受碰摩点轴心轨迹的影响也迅速增大,增大的碰摩力更加剧了碰摩截面的不平衡热分布,此时转子的振动处于一种恶性循环的状态.从转子截面碰摩热流的周向分布可知,最大热流在300°左右,这样由热弯曲造成的不平衡量和转子的不平衡量(0°)形成60°角,加大了不平衡总量,使得转子的振动逐渐增大至最终发散.

由转子碰摩截面的最大温差曲线及热弯矩变化曲线可以看出,热弯矩受最大温差影响较大,与其变化基本保持一致,后期转子的整周碰摩加剧使得最大温差逐渐变小,热弯矩也随即减小,但此时转子的不平衡总量很大,转子振动处于快速发散期,热弯矩的变化则对其影响不大.

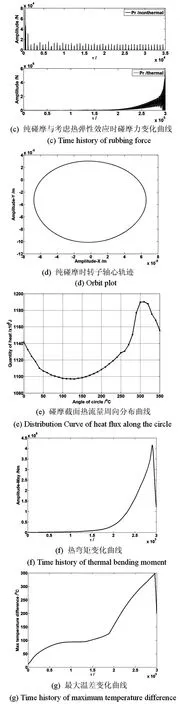
图8 低于临界转速时(w=150rad/s)碰摩仿真结果Fig.8 Rubbing simulation results for w=150rad/s below the critical speed

3.2 接近临界转速时的摩擦振动

图9所示为转子接近临界转速运行时发生碰摩的仿真结果,与转子低于临界转速运行时的碰摩仿真结果相差不大,但对比纯碰摩的转子轴心轨迹可以看出,此时转子发生严重的碰摩,振动幅值和碰摩力都远大于低于临界转速运行时的碰摩.因此转子的热弹性效应变得非常明显,又由于此时的热弯曲不平衡量在260°左右,与原始不平衡力合成之后使得不平衡总量加大,短时间内便造成转子振动发散.计算转子和静子摩擦生热温度场时,采用以下假设：(1)不考虑摩擦过程中材料的磨损；(2)转子和静子材料满足各向同性；(3)忽略由于温度变化引起的转子物性参数的变化；(4)不考虑热量沿轴向的传播.

图9 接近临界转速时(w=150rad/s)碰摩仿真结果Fig.9 Rubbing simulation results for w=150rad/s close to the critical speed

3.3 高于临界转速时的摩擦振动

图10所示为转子高于临界转速运行时发生碰摩的仿真结果.由图可见,相比较前面两种情况考虑热弹性效应下的转子碰摩有较大不同.由于摩擦产生的热弯曲和原始不平衡力的夹角在200°左右,两者合成之后,不平衡力减小,振动逐渐减小.受截面最大温差的影响,热弯矩前期快速增大,之后由于转子碰摩位置不断变化,最大温差保持不变,但热弯矩受其他碰摩区域影响则逐渐减小,最后摩擦几乎消失,热弯矩则保持恒定.

图10 高于临界转速时(w=150rad/s)碰摩仿真结果Fig.10 Rubbing simulation results w=150rad/s above the critical speed

4 小结

本文依据转子碰摩理论建立了一种简单的求解碰摩截面热分布的计算模型,并对低于、接近和高于临界转速下碰摩热弯曲转子的动力学特性进行了数值仿真研究.结果表明:转子在低于和接近临界转速运行发生碰摩后,热弯矩和原始不平衡力合成后加大不平衡量,会使得转子的振动由平稳状态逐渐发散;接近临界转速时的情况更甚,转子在这两种情况下出现的碰摩对机组安全运行危害很大;转子在高于临界转速运行发生热碰摩时与前两者有较大不同,由于摩擦产生的热弯矩和原始不平衡力合成之后,不平衡力减小,使得转子振动逐渐减小,所以转子在高于临界转速运行时发生碰摩相对其他两种情况较安全.

1朱向哲,袁惠群,李东. 摩擦热效应对航空发动机高压转子系统碰摩响应的影响. 推进技术, 2010,31(3):366～371 (Zhu X Z, Yuan H Q, Li D. Friction thermal effect on rubbing response of a high pressure rotor system.JournalofPropulsionTechnology, 2010,31(3):366～371 (in Chinese))

2张楠,刘占生,姜兴渭. 高速转子轴承系统碰摩故障仿真研究. 振动与冲击, 2010,29(9):77～81 (Zhang N, Liu Z S, Jiang X W. Study on the rub-impact fault of the high-speed rotor-bearing system.JournalofVibration&Shock, 2010,29(9):77～81(in Chinese))

3田永伟,杨建刚. 基于特征值分析的摩擦转子热稳定性研究. 振动与冲击, 2010,29(7):66～68 (Tian Y W, Yang J G. The mal stability of a rubbing rotor based on eigenvalue analysis.JournalofVibration&Shock, 2010,29(7):66～68 (in Chinese))

4黄葆华,杨建刚,高亹. 摩擦热弯曲对转子稳定性的影响. 振动工程学报, 2001,14(1):23～28 (Huang B H, Yang J G, Gao W. Influence of thermal bow on the stability of rubbing bearing-rotor system.JournalofVibrationEngineering, 2001,14(1):23～28 (in Chinese))

5王士敏,陆启韶. 转子通过临界转速时碰摩热效应对振动特性的影响. 动力学与控制学报, 2004,2(3):64～69 (Wang S M, Lu Q S. The effect of rub-impact thermal effects on vibration characteristics of a rotor passing through critical speed.JournalofDynamicandControl, 2004,2(3):64～69 (in Chinese))

6梁明轩,袁惠群. 滚动轴承-柔性碰摩转子系统非线性动力学响应分析. 动力学与控制学报, 2013,11(2):153～158 (Liang M X, Yuan H Q. Nonlinear dynamic response on rotor system of ball bearing-flexible rub.JournalofDynamicandControl, 2013,11(2):153～158 (in Chinese))

7Goldman P, Muszynska A. Chaotic behavior of rotor/stator systems with rubs.JournalofEngineeringforGasTurbinesandPower, 1994,116(3):692～701

8Kellenberger, W. Spiral vibrations due to the seal rings in turbogenerators thermally induced interaction between rotor and stator.JournalofMechanicalDesign, 1980,102(1):77～184

9Childs D W. A note on Kellenberger′s model for spiral vibrations.JournalofVibrationandAcoustics, 2001,123(3):405～408

10 Fay R, Kreuzer D, Liebich R. The Influences of thermal effects induced by the light-rub against the brush seal to the rotordynamics of turbo machines. In: ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, 2014:V07AT31A008-V07AT31A008

11 Kreuzer D, Fay R, Liebich R, et al. Investigations on non-steady behaviour of rotors due to light rubbing to brush seals. In: Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, 2015:1993～2005

12 Chen J M, Jiang D X, Deng T T, et al. Dynamic response of rubbing happening in a flexible rotor-bearing system. In: 2015 International Conference on Electrical, Automation and Mechanical Engineering, 2015:168～171

13 钟一谔,何衍宗,王正等. 转子动力学. 北京:清华大学出版社, 1987:21～24 (Zhong Y E, He Y Z, Wang Z, et al. Rotor dynamics. Beijing: Tsinghua University Press, 1987:21～24 (in Chinese))