On Approximation by Two Kinds Modi fied Durrmeyer Rational Interpolation Operators inSpaces
2018-07-06
(Department of Mathematics,Inner Mongolia Normal University,Huhhote 010022,China)
§1. Introduction and main results
Letbe the weighted Orlicz spaces,the weight function isForits Orlicz norm is de fined as[1]

or
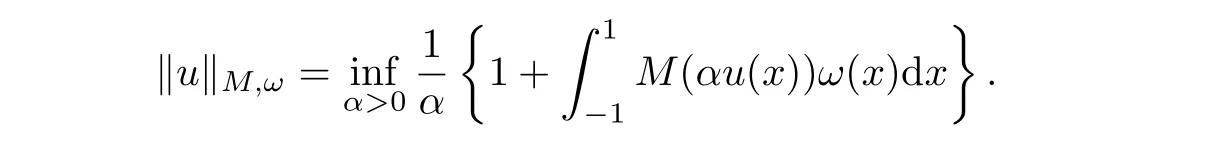
The Luxemburg norm

is equivalent to the Orlicz norm asholds true.
denotes the modulus of continuity of f in Orlicz spaces,that is

Sun Zhiling[2]discussed the approximation of Nevai-Kantorovich rational interpolation operator in weighted Orlicz spaces.In 2009,Gu Chunhe[3]studied the approximation theorem of the first kind of modi fied Vertesi-Kantorovich operator in Orlicz spaces which is formed by the Lagrange interpolation basis function of the first kind of Chebyshev polynomial.In 2010,Feng Yue[4]studied the approximation theorem of shepard-Kantorovich operator in Orlicz space.In the second chapter of[5],not only the de finition of Shepard-Durrmeyer,Vertesi-Durrmeyer and Nevai-Durrmeyer rational interpolation operators are given by Cheng Wentao,but also the approximation theorems of three kinds of operators in Lp(1≤p<∞)spaces were proved in 2012.Therefore,on the basis of the literature[5],we study the approximation problems of two kinds of Durrmeyer rational interpolation operators inspaces.
Let η(x)be a generalized smooth Jacobi weight function de fined by

where −1
For anythe modi fied Nevai-Durrmeyer operator is de fined as

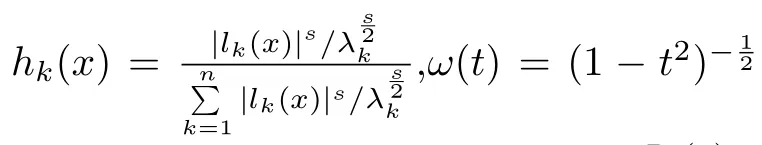
For anyde fine the modi fied Shepard-Durrmeyer operators as


Theorem 1.1Let,then

Write

Here and throughout the whole paper,we use Csto indicate a positive constant depending only on s,Cλ,to indicate a positive constant depending only on λ,and C is an absolute positive constant,their values may vary in de ff erent occurences even in the same line.
§2. Preliminaries
In order to proof theorem,we need the following lemmas.
Let x0=1,xn+1= −1,also xk,k=1,2,···,n,be the zeros of pn(u).Set xk=cosθk,then θk∈ [0,π],k=0,1,···,n+1 and

Lemma 2.1[5,6]For any x∈[xj+1,xj],0≤j≤n,0≤k≤n,we have
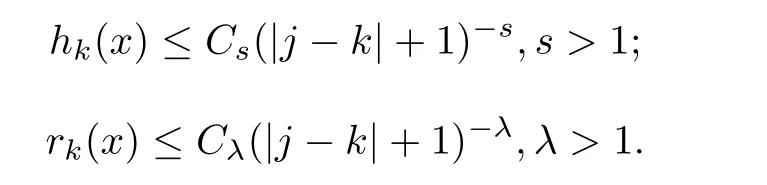
Lemma 2.2[5,6]Let x=cosθ,θ∈ [0,π],we have
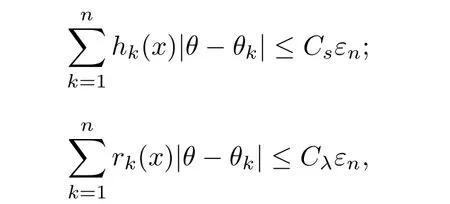
where
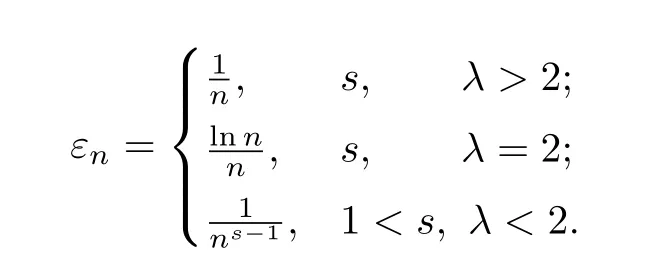
Lemma 2.3For s,λ >1,Dn(f,x),Sn(f,x)are positive bounded linear operators in,that is,for anywe have



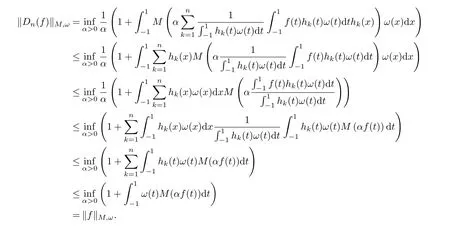

Let g(θ)=f(cosθ),by using Jackson operators,we can easily obtain the following lemma.
Lemma 2.4[3]Letbe an even function,then there exists an even trigonometric polynomial TN(θ)with degree ≤ N,such that

Lemma 2.5Let PN(x)be a polynomial whose order is less than or equal to N,and TN(θ)=PN(cosθ),then
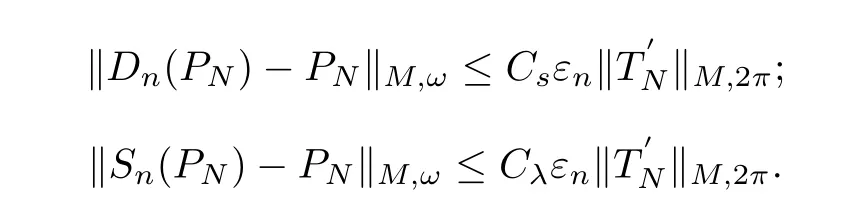
ProofLet x=cosθ,t=cosυ,θ,υ ∈ [0,π],because of Dn(f,x)=1,we have
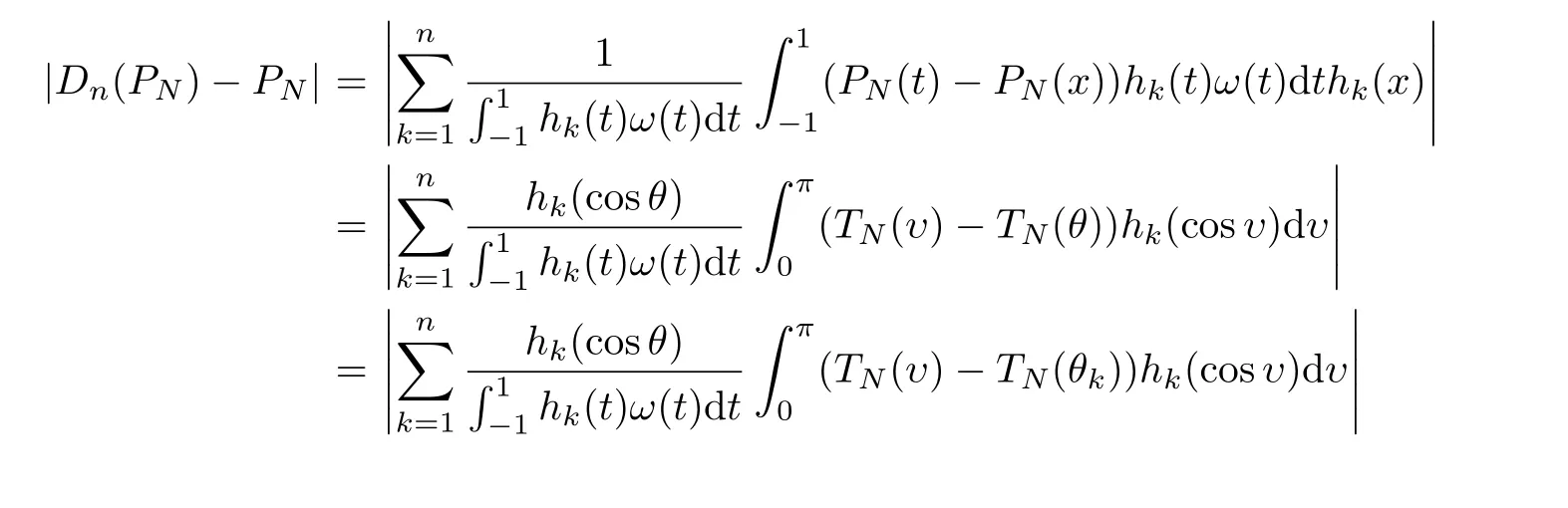

whereare the Hardy-Littlewood extremal maximum function of
By lemma 2.3,we obtain

There is another constant C,satis fiesby lemma 2.3,we obtain

Similarly available
§3.Proof the Theorem
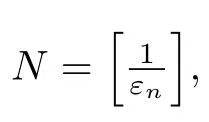


Similarly available
[1]WU Cong-xin,WANG Ting-fu.Orlicz space and its application[M].Harbin:Heilongjiang Science and Technology Press,1983.
[2]SUN Zhi-ling.Approximation theorems of modi fied Nevai operators in Orlicz spaces[J].Journal of Inner Mongolia University for the Nationalities(NATURAL SCIENCE EDITION),2007,22(2):121-124.
[3]GU Chun-he.Study on some approximation problems in Orlicz spaces[D].Hohhot:School of Mathematical Sciences,Inner Mongolia Normal University,2009.
[4]FENG Yue.Approximation equivalence theorem of Shepard operator in Orlicz spaces[J].journal of inner mongolia normal university2010,39(6):565-568.
[5]CHENG Wen-tao.Approximation theorems of modi fied rational operators[D].Zhejiang:School of mathematics,Zhejiang Sci-Tech University,2012.
[6]ZHOU Guan-zhen.Approximation of a kind of Nevai-Durrmeyer operators in spaces[J].Analysis in Theory and Applications2005,21(3):294-300.
[7]A.-R.K.RAMAZANOV.On approximation by polynomials and rational functions in Orlicz spaces[J].Analysis Mathematica,1984,10:117-132.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Common Fixed Point Results for Quasi-contractions Involving Altering Distance Functions in Ordered Cone Metric Spaces
- Some Generalized Normal Subgroups and p-nilpotency of Finite Groups
- The Growth Order of Solutions of Systems Complex Di ff erence Equations
- The{P,k+1}-re flexive Solution to System of Matrix Equations AX=C,XB=D
- The Credibility Estimators under MLINEX Loss Function
- Implicative Pseudo Valuations on Hoops
