Common Fixed Point Results for Quasi-contractions Involving Altering Distance Functions in Ordered Cone Metric Spaces
2018-07-06
(School of Mathematics and Information Science,Leshan Normal University,Leshan 614000,China;School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
§1. Introduction
As a fundamental result in fixed point theory,Banach contraction mapping principle is extended and generalized by many authors in various directions.Alber Y and Guerre-Delabriere S[1]introduced the concept of weakly contractive mappings and proved some fixed point theorems in Hilbert spaces.Rhoades B E[2]studied the fixed point problems of weakly contractive mappings and obtained some fixed point theorems in complete metric spaces.After Khan M S et al[3]introduced the notion of altering distance functions in metric spaces,some more general contractive conditions were studied.At the same time,many authors also studied common fixed point problems for two or more mappings satisfying certain contractive conditions,and some fixed point and common fixed point results for mappings satisfying weakly contractive conditions were obtained(see[4-7]).The initial research of common fixed point problems depended on the assumption that all of maps are commutative,Jungck G[8]de fined the concept of weakly compatible pairs of mappings,which is weaker than commutativity.Recently,several authors studied generalized weak contractive mappings in an ordered metric space which is a metric space endowed with a partially ordering,and obtained some coincidence point results.For details,see[9-12].The notion of cone metric spaces was introduced by Huang L G et al[13]and some fixed point theorems were obtained in cone metric spaces.Subsequently,some fixed point and common fixed point results were generalized from metric spaces to cone metric spaces.Han Y et al[14]obtained some new theorems for Lipschitz type mappings in cone metric spaces.Choudhury B S et al[15-16]generalized the notion of altering distance functions from metric spaces to cone metric spaces and obtained some fixed point and common fixed point results for generalized weak contractive mappings in cone metric spaces or in partially ordered cone metric spaces.In this paper,we shall show that some common fixed point results for four mappings satisfying quasi-contractive conditions under an altering distance function in partially ordered cone metric spaces.
§2. Preliminaries
Let E be a real Banach space,P a subset of E,and θ the zero element in E.If
(i)P is closed,nonempty and
(ii)a,b∈R,a,b≥0 and x,y∈P imply that ax+by∈P;
(iii)x∈P and−x∈P imply that x=θ;then P is called a cone.We denote the interior of P by intP.If intP is called a solid.
接受新教学法实习学生的理论知识及临床技能分数,均优于传统教学法组学生,差异具有统计学意义(P<0.05),见表1。
Given a cone P⊂E,we can de fine a partial ordering“≤”with respect to P on E as follows:x≤y if and only if y−x∈P,x 在流行病学实践教学中开展PBL教学能够加深学生对流行病学现场调查的理解和应用,学会专业文献查阅方法,从而掌握以解决问题为中心、多种学习途径相整合的学习方法;通过团队内和团队间交流,培养学生团队精神;通过PBL教学,培养学生运用流行病学知识和技能解决实际问题的能力;PBL教学中小组总结的过程也对学生课题分析、语言表达及写作能力的培养具有重要意义[3,4]。由此可见,PBL教学在流行病学实践教学中的应用,不仅充分发挥了流行病学学科特点,加深学生对理论知识的理解,而且能够通过学生的自我学习和再学习,使其在未来的医学实践与职业生涯中尽快适应工作要求,并为持续学习奠定良好基础。 The cone P is said to be normal if there is a number K>0 such that for all x,y∈E,θ≤x≤y impliesThe least number satisfying this inequality is called the normal constant of P.The cone P is said to be regular if every increasing sequence which is bounded from the above is convergent,that is,if{xn}is a sequence such that x1≤ x2≤ ···≤ xn≤ ···≤p for some p∈E,then there exists x∈E such that kxn−xk→0 as n→∞.Equivalently,the cone P is regular if and only if every decreasing sequence which is bounded from the below is convergent.Every regular cone is a normal cone. De finition 2.1[13]Let X be a nonempty set,E a real Banach space and P a cone in E.Suppose the mapping d:X×X→E satis fies following conditions. (i)θ≤d(x,y)for all x,y∈X and d(x,y)=θ if and only if x=y; (ii)d(x,y)=d(y,x)for all x,y∈X; (iii)d(x,y)≤d(x,z)+d(z,y)for all x,y,z∈X;then d is called a cone metric on X and(X,d)is called a cone metric space. 根据本组研究结果,我们认为在采用注射器抽吸负压状态下同轴取材活检更容易成功,并且不增加穿刺活检相关并发症,而有助于明确椎体压缩骨折病因,减少椎体压缩骨折病因的误诊和漏诊,使患者获得更长期的良好疗效。因此,经皮椎体成形术中在负压状态下同轴取材活检是一种安全易行、提高诊断准确性的活检方法,应该在椎体压缩骨折行椎体成形术时常规进行。 ψ :P → P is an altering distance function and ϕ :intP ∪{θ} → intP ∪ {θ}is a continuous function with the properties as follows. By a same arguments as in Caes 2,we get r=θ.Therefore 本部分控制契约弹性系统α、β为常量,令p0+a(μH-Q)+g-v-cr-cd-λ1>0.当市场需求增大时,根据公式(29),供应链期望收益表达式为 (ii){xn}is a Convergent sequence if for every c in E with θ¿ c,there is a positive integer number N such that d(xn,x)¿c for all n>N and some point x in X.We denote this byor xn→x as n→∞. A cone metric space X is said to be complete if every Cauchy sequence in X is convergent. Proposition 2.1[13]Let(X,d)be a cone metric space and P a normal cone with normal constant number K.Let{xn}be a sequence in X.Then (i){xn}converges to x for some x∈X if and only if d(xn,x)→θ(n→∞). (ii){xn}is a Cauchy sequence if and only if d(xn,xm)→θ(n,m→∞). Remark 2.1Let E be a real Banach space with cone P.The following properties are often used. Similarly,we can obtain that (ii)Let a,b,c∈E.If a≤b and b¿c,then a¿c. (iii)Let a∈E.If θ≤ a¿c for each c∈ intP,then a= θ. (iv)Let a∈ P and λ be a real number with 0< λ <1.If a≤ λa,then a= θ. (v)Let θ≤ x ≤ y and a be a real number with a≥ 0,then θ≤ ax ≤ ay. (vi)Let θ ≤ xn≤ ynfor n=1,2,···,and limn→∞xn=x,limn→∞yn=y,then θ ≤ x ≤ y. (vii)P is a normal cone if and only if xn≤ yn≤ znand limn→∞xn=limn→∞zn=w imply limn→∞yn=w. De finition 2.3[16]Let ψ :P →P be a function. (i)ψ is called strongly monotone increasing if x ≤ y if and only if ψ(x)≤ ψ(y)for all x,y∈P. 采用现代信息技术对机械类课程中复杂产品设计、机械加工过程、机械振动控制以及加工表面质量等知识点进行建模和仿真,可以有效提高教学效率并增强教学直观性。另外,机械类课程中的工艺流程、机床夹具、加工精度、机器装配等教学内容,都可以通过该方法来实现。因此,该课程数字化和可视化的实施,对机械类专业课程的教学改革具有一定的借鉴价值。 (ii)ψ is said to be continuous at x0∈P if for any sequence{xn}in P,xn→x0implies ψ(xn)→ψ(x0)as n→∞. De finition 2.4[16]The function ψ :P →P is called an altering distance function if (i)ψ is continuous and strongly monotone increasing. 张清元觉得,唐小芹是孤儿院里最漂亮的女孩。她比那帮小家伙要大一些,但比张清元要小。黎院长就叫她小芹子。小芹子是一个从下江逃难来的女人留在河口的。张清元第一次见到小芹子是在河口。他之所以能记住小芹子,是因为她的嘴唇上长有一颗鲜亮突起的黑痣,圆圆的。他听大人们说过,那颗痣就叫美人痣,乍一看有些刺眼,但看过之后就觉得这女孩漂亮,过目难忘。 (ii)ψ(t)= θ if and only if t= θ. 大数据时代下的开放性创新实验室教学管理,其不仅仅只是展现在实验设备上面的革新,它往往还会出现在教学模式上,具体来讲也就是,相关教师可以根据大数据的信息,科学有效的提前做好有关实验器材设备的准备工作,并且在具体的实验开展过程中,明确的了解学生的实验数据,这是因为学生所研究的实验,最终都会以数据的形式保存在相应的数据信息库当中,这种信息的保存与每位学生都是相互联系的,这样大大地方便了教师的研究观察。 Proposition 2.2[15]Let(X,d)be a cone metric space and P a regular cone such that d(x,y)∈ intP for x,y ∈ X withSuppose that function ϕ :intP ∪ {θ} → intP ∪{θ}satis fies the following properties. (i)ϕ(t)= θ if and only if t= θ; (ii)ϕ(t)¿t for t∈ intP; 家长进行家长助教时要做好充分的物质准备,教师应该指导家长准备好充足的物质材料,并且明确各个材料投放的具体环节,对教材的应用做到心中有数。如,对于幼儿的操作材料,教师应该先告知家长班级人数,请家长按照多于班级人数的份额准备材料,并按小组分门别类地放好,以方便操作。让家长做好充足的物质准备,便于活动开展。 (iii)Either ϕ(t)≤ d(x,y)or d(x,y)≤ ϕ(t)for t∈ intP ∪{θ}and x,y∈ X. If{xn}is a sequence such that{d(xn,xn+1)}is monotonic decreasing,thenis convergent to either r=θ or r∈intP. De finition 2.2[13]Let(X,d)be a cone metric space,{xn}is a sequence in X.We say that Proposition 2.3[16]Let(X,d)be a cone metric space and ϕ :intP ∪{θ}→ intP ∪{θ}be a function with following properties. (i)ϕ(t)= θ if and only if t= θ; (ii)ϕ(t)¿t for t∈ intP. Then a sequence{xn}in X is a Cauchy sequence if and only if for each c∈ E with θ¿ c,there exists a positive integer number n0such that d(xn,xm)¿ ϕ(c)for all n>m>n0. De finition 2.5[17]Let(X,„)be a partially ordered set and F,G,H:X → X be mappings such that F(X)⊆H(X)and G(X)⊆H(X).We say that F and G are weakly increasing with respect to H,if for all x∈X,we havefor each y∈H−1(Fx)andfor each y∈H−1(Gx).If F=G,we say that F is weakly increasing with respect to H. De finition 2.6[10]Letbe a partially ordered set and F,G,H:X → X be mappings such that F(X)⊆H(X),(F,G)is said to be partially weakly increasing with respect to H,if for allfor any y∈H−1(Fx). Let X be a nonempty set and F,G:X→X be two mappings.If w=Fx=Gx for some x in X,then x is called a coincidence point of F and G,and w is called a point of coincidence of F and G. De finition 2.7[18]The mappings F,G:X→X are weakly compatible if,for every x∈X,FGx=GFx holds whenever Fx=Gx,that is,F and G commute at every their coincidence point.We say that{F,G}is a weakly compatible pair. A partially ordered cone metric space is a cone metric space(X,d)endowed with a partial ordering,we denoted it by(X,„,d). 句中“驰说之言从横者”,不能按顺序翻译。“言从横”为定语,“驰说”为中心语,“之……者”为定语后置的标志。翻译时应按现代汉语的表达习惯调整为“言从横”的“驰说”。句意:致力于加强军事力量,揭穿主张合纵连横的往来奔走的游说之客。 De finition 2.8Let(X,„,d)be a partially ordered cone metric space and F:X → X be a mapping.We say that F has the property(A)if{xn}is a sequence in X such that{Fxn}is a nondecreasing sequence,converging to Fx0for some x0∈ X,thenfor n=1,2,···,and 作为欧洲化学公司深入中国市场的前沿,欧化农业贸易(深圳)有限公司在中国开拓新的钾肥贸易渠道的突破上一直不遗余力。丁振军介绍,“目前公司红粉、红颗粒、白粉、白色结晶等产品都将随着产能的释放陆续问世,此后如何进军国内市场,公司一直在尝试开拓新的渠道。”国际贸易是中国化肥行业发展的必然,中国化肥企业在国内市场竞争激烈的情况下,正在全球各个地区通过各种方式探寻“走出去”之路,同时也极力寻求新技术、优质资源“走进来”。“通过多元化产品释放钾也是公司目前在进行的工作。” Let X be a set and F,G,T,S:X→X be four mappings such that F(X)⊆T(X),and G(X)⊆S(x).Let x0be a arbitrary point in X,then there exist x1,x2∈X such that Fx0=Tx1,Gx1=Sx2.By the induction,we can construct two sequences{xn},{yn}in X such that y2n=Fx2n=Tx2n+1,y2n+1=Gx2n+1=Sx2n+2,n=0,1,2,···.{yn}is called a(F,G)−(T,S)-sequence with initial point x0.We always suppose that P is a solid in E. Theorem 3.1Letbe a partially ordered complete cone metric space and P a regular cone such that d(x,y)∈intP for x,y∈X withSuppose that F,G,S,T:X→X are four mappings such that F(X)⊆T(X),G(X)⊆S(X)and,both T(X)and S(X)are closed subsets in X.If the following conditions are satis fied. (1)There exists u(x,y)∈MF,G,S,Tsuch that for x,y∈X such that Sx and Ty are comparable,where 722 Research progress of mesenchymal stem cell-derived exosomes in kidney diseases (i)ϕ(t)= θ if and only if t= θ; (ii)ϕ(t)¿t for t∈ intP; (iii)Either ϕ(t)≤ d(x,y)or d(x,y)¿ ϕ(t)for t∈ intP ∪{θ}and x,y∈ X; (2)(F,G)is partially weakly increasing with respect to T and(G,F)is partially weakly increasing with respect to S; (3)S and T have the property(A); (4){F,S}and{G,T}are weakly compatible pairs. Then F,G,S and T have a common fixed point. ProofLet x0be a arbitrary point in X,and{yn}be a(F,G)−(T,S)-sequence with initial point x0.Sincefrom the condition(2),we can obtain that.Hence,Sx2nand Tx2n+1are comparable.From(3.1),we have where and n=1,2,···.For every n,there are three possible cases. Case 1Then By using the strongly monotone property of ψ,we have Case 2Then From the strongly monotone property of ψ,it follows thatwhich implies that Case 3By using triangular inequality,d(y2n−1,y2n+1)≤then Also we can obtain that (i)Let a,b,c∈E.If a¿b and b¿c,then a¿c. From(3.3)and(3.4),{d(yn+1,yn)}is a monotonic decreasing sequence.By Proposition 2.2,there exists r∈P with either r=θ or r∈intP such that d(yn+1,yn)→r as n→∞. Next,we show that r=θ.Since 徐锦霞[17]认为无障碍网络课程是一种新的网络课程的视角,最终实现无论何人何时何地都能学习的无障碍网络教学模式。 for n=1,2,···.(3.2)implies that there is a sequence{nk}of positive integer numbers with nk 点击菜单[选择][按位置选择],打开选择对话框,在[目标图层]勾选建筑物层,[源图层]选择阴影栅格转换而成的矢量图层,[空间选择方法]应选 “目标图层要素的质心在源图层要素内”;根据需要,设置其余参数,点击 [确认]完成查询。建筑物已选中。右击查询后的建筑物图层,选择[数据]→[导出数据],打开工具对话框,完成设置,输出不符合规范的建筑物。如图12中,深色表示不符合规定的建筑。 Case 1for k=1,2,···.By taking k → ∞ in the inequality above,we have ψ(r)≤ ψ(r)− ϕ(r)from the continuity of ψ and ϕ,and Remark 2.1(vi).Hence ϕ(r)= θ,that is,r= θ. Case 2for k=1,2,···.By taking k → ∞ in the inequality above and using the continuity of ψ and ϕ,and Remark 2.1(vi),also we have ψ(r)≤ ψ(r)− ϕ(r).So r= θ. Case 3for k=1,2,···.By using the triangular inequality,.From the strongly monotonic property,we obtain that (i){xn}is a Cauchy sequence if for every c in E with θ¿ c,there is a positive integer number N such that d(xn,xm)¿c for all n,m>N. as n→∞.Now,we show that{yn}is a Cauchy sequence.From(3.5),it is sufficient to prove that{y2n}is a Cauchy sequence.If not,by proposition2.3,there exists c ∈ E with θ¿ c such that,for each positive integer number k,there exist positive integer numbers nkand mkwith nk>mk>k such that d(y2mk,y2nk)¿ ϕ(c)is not true.From a property of ϕ,we have ϕ(c)≤ d(y2mk,y2nk).For further,we can choose nksuch that nkis the smallest in such positive integer numbers,then On the other hand,by using the triangular inequality,we obtain By taking k→∞in(3.7)and using Remark 2.1(vii),we get as k→∞.Similarly,by using the triangular inequality,we can also obtain and By taking k→∞in the six inequalities above and using Remark 2.1(vii),we have and as k→∞.Since Sx2nkand Tx2mk+1are comparable,from(3.1),we have where and k=1,2,···.There is a sequence{ki}of positive integer numbers with ki Case 1for i=1,2,···.ThenBy taking i→ ∞ and using(3.9),(3.10)and the continuity of ψ and ϕ,we get ψ(ϕ(c))≤ ψ(ϕ(c))− ϕ(ϕ(c)),hence ϕ(ϕ(c))= θ.It yields that c=θ. Case 2for i=1,2,···.Then By taking i→ ∞ and using(3.5),(3.9),(3.10)and the continuity of ψ and ϕ,we have ψ(ϕ(c))≤ψ(θ)− ϕ(ϕ(c)).Since θ≤ ψ(ϕ(c)),we get ϕ(ϕ(c))= θ,that is,c= θ. Case 3for i=1,2,···.Then By taking i→ ∞ in the inequality above and using(3.8)∼(3.11)and the continuity of ψ and ϕ,we obtain ψ(ϕ(c))≤ ψ(ϕ(c))− ϕ(ϕ(c)),which is true unless ϕ(ϕ(c))= θ.Hence c= θ. Now we come to a contradiction,therefore{yn}is a Cauchy sequence. From the completeness of X,there exists a point w∈X such that yn→w as n→∞.Since y2n∈T(X),y2n+1∈S(X)and,T(X)and S(X)are closed in X,there exist z1,z2∈X such that w=Tz1=Sz2.From the condition(3)of the theorem,Tx2n+1and Sz2(=Tz1)are comparable.By(3.1),we have where and n=1,2,···.There is a sequence{nk}of positive integer numbers with nk+1>nk(k=1,2,···)such that the one of following three cases is true: Case 1fork=1,2,···.ThenBy taking k → ∞ and using the continuity of ψ and ϕ,we obtain ψ(d(Fz2,w)≤ ψ(θ)−ϕ(θ)= θ.So d(Fz2,w)= θ,that is,Fz2=w. Case 2for k=1,2,···.Then By taking k → ∞ in the inequality above,we getFrom the strongly monotone property of ψ,d(w.Fz2)= θ.So Fz2=w. Case 3for k=1,2,···.Then By taking k → ∞ in the inequality above,also we obtainHence Fz2=w.Therefore,Fz2=Sz2=w,z2is a coincidence point of F and S and w is a point of coincidence of F and S. Similarly,since Sx2nand Tz1(=Sz2)are comparable from the condition(3)of the theorem,as we do it in the above,we can obtain that z1is a coincidence point of G and T and w is a point of coincidence of G and T. If F and S are weakly compatible,then Sincefrom(3.1)and(3.12),we have where If u(w,z1)=d(Fw,w),then ψ(d(Fw,w))≤ ψ(d(Fw,w))−ϕ(d(Fw,w)).From the strongly monotone property of ψ,we have ϕ(d(Fw,w))= θ,which implies that d(Fw,w)= θ.Hence Fw=w. If u(w,z1)= θ,then ψ(d(Fw,w)) ≤ ψ(θ)− ϕ(d(Fw,w))= −ϕ(d(Fw,w)).Since θ ≤ψ(d(Fw,w)),which means that ϕ(d(Fw,w))= θ.Also we have Fw=w. From(3.12),we can obtain that Sw=Fw=w.Similarly,we have Tw=Gw=w from that G and T are weakly compatible,that is,w is a common fixed point of F,G,S and T. This completes the proof of the theorem. Corollary 3.1Letbe a partially ordered complete cone metric space and P a regular cone such that d(x,y)∈intP for x,y∈X withSuppose that F,G,H:X→X are three mappings such that F(X)⊆H(X),G(X)⊆H(X)and H(X)is a closed subset in X.If the following conditions are satis fied. (1)There exists u(x,y)∈ MF,G,Hsuch that ψ(d(Fx,Gy))≤ ψ(u(x,y))−ϕ(d(Hx,Hy))for x,y∈X such that Hx and Hy are comparable,where ψ :P → P is an altering distance function and ϕ :intP ∪{θ} → intP ∪ {θ}is a continuous function with the properties as in Theorem 3.1. (2)F and G are weakly increasing with respect to H; (3)H has the property(A); (4){F,H}and{G,H}are weakly compatible pairs. Then F,G and H have a common fixed point. ProofBy setting S=T=H in Theorem 3.1,we know that the conclusions in the Corollary are true. Corollary 3.2Letbe a partially ordered complete cone metric space and P a regular cone such that d(x,y)∈intP for x,y∈X withSuppose that F,S,T:X→X are three mappings such that F(X)⊆S(X),F(X)⊆T(X)and,both S(X)and T(X)are closed subsets in X.If the following conditions are satis fied. (1)There exists u(x,y)∈ MF,S,Tsuch that ψ(d(Fx,Fy))≤ ψ(u(x,y))−ϕ(d(Sx,Ty))for x,y∈X such that Sx and Ty are comparable,where ψ :P → P is an altering distance function and ϕ :intP ∪{θ} → intP ∪ {θ}is a continuous function with the properties as in Theorem 3.1. (2)F is weakly increasing with respect to S as well as T; (3)S and T have the property(A); (4){F,S}and{F,T}are weakly compatible pairs. Then then F,S and T have a common fixed point. ProofBy setting F=G in Theorem 3.1,we know that the conclusions in the corollary are true. Example 3.1Let E=R2with usual norm,then E is a Banach space with the zero element θ=(0,0).Let P={(x,y):x,y ≥ 0},then P is a regular cone in E.Let X=[0,1]be a partially ordered set with orderingwhich is de fined by for all x,y∈X,where“≤”is the usual ordering.We de fine d:X×X→E as follows for x,y∈X,then(X,d)is a complete cone metric space and d(x,y)∈intP for x,y∈X withLet ψ :P → P and ϕ :intP ∪{θ} → intP ∪{θ}be two functions de fined by for t∈ P and s∈ intP ∪{θ},where t=(t1,t2),s=(s1,s2)and v=min{s1,s2}. Then ψ and ϕ are continuous functions, ψ(t)= θ if and only if t= θ and ψ is strongly increasing.If ϕ(s)= θ,then v=0.Note that s=(s1,s2) ∈ intP ∪ {θ}.So s1=s2=0,therefore s=θ. For(s1,s2)∈ intP ∪ {θ}and x,y ∈ X,we suppose that ϕ(s)≤ d(x,y)is not true,thenthat is,ϕ(s)∈ intP andwhich implies that(|x−y|,|x−y|)¿that is,d(x,y)¿ ϕ(s). Now,we de fine the four mappings from X to X as follows:for all x∈X and Then S(X)and T(X)are closed in X,F(X)⊆T(X)and G(X)⊆S(X).Clearly,{F,S}and{G,T}are weakly compatible pairs of mappings. Let{Sxn}be a nondecreasing sequence,converging to Sz.Ifthenas n→ ∞,that isas n→ ∞,it implies thatas n→∞in R which is the real number space.Since{Sxn}is a nondecreasing sequence,we haveand sofor all n=1,2,···.Clearly,.If,also we haveandHence,S has the property(A).Similarly,also T has the property(A).Since It is easy to check that,for all x,y∈ X,ψ(d(Fx,Gy))≤ψ(u(x,y))−ϕ(d(Sx,Ty))holds.By Theorem 3.1,F,G,S and T have a common fixed point Lemma 3.1Letbe a partially ordered complete cone metric space and P a regular cone such that d(x,y)∈ intP for x,y ∈ X withLet ϕ :intP ∪{θ}→ intP ∪{θ}be a continuous function with the properties as follows. (i)ϕ(t)= θ if and only if t= θ; (ii)ϕ(t)¿t for t∈ intP; (iii)Either ϕ(t)≤ d(x,y)or d(x,y)≤ ϕ(t)for t∈ intP ∪{θ}and x,y∈ X. Suppose that w is a point and{yn}is a sequence in X such that{d(w,yn)}is monotonic decreasing.Then{d(w,yn)}is convergent to either r=θ or r∈intP. ProofSince P is a regular cone,and{d(w,yn)}is a decreasing sequence which is bounded from the below,there exists r∈P such that d(w,yn)→r as n→∞.If there exists n0such that d(w,yn0)= θ,then d(w,yn)= θ for n>n0,and so r= θ.Therefore,we can suppose that d(w,yn)∈ intP for n=1,2,···. LetSince P is a regular cone,it is also a normal cone.Let B={t∈ intP:ktk Hence,from the condition(iii)of the lemma,we have ϕ(t) ≤ d(w,yn)for t ∈ B and n=1,2,···.Let n → ∞ in the inequality,we get ϕ(t) ≤ r for t∈ B.Since ϕ(t) ∈ intP for t∈ intP,we havethat is,r∈ intP. Theorem 3.2Letbe a partially ordered complete cone metric space,and P a regular cone such that d(x,y)∈intP for x,y∈X withLet F,G,S and T:X→X be four mappings satisfying conditions(1)∼(4)in Theorem 3.1.If following condition(5)is also satis fied. (5)For x,y∈S(X)∩T(X),there exists z0∈X such thatandwhere-sequence with initial point z0andis a(G,F)−(S,T)-sequence with initial point z0. Then the common fixed point of F,G,S and T is unique. ProofLet w1and w2be two common fixed points of F,G,S and T. If w1and w2are comparable,that is,Sw1and Tw2are comparable,then there existssuch that where Thenwhich implies that ϕ(d(w1,w2))=0.Hence d(w1,w2)=0,that is,w1=w2. If w1and w2are not comparable,then there exists a point z0∈X such thatandandwhere{yn}is a(F,G)−(T,S)-sequence with initial point z0andis a(G,F)−(S,T)-sequence with initial point z0.There exist two sequenceswithsuch that and where n=0,1,2,···.As we do it in the proof of Theorem 3.1,we can prove that Since,and,we get.From(3.1),we have where and n=1,2,···.For every n,there are three possible cases. Case 1From(3.14),we haveBy using the strongly monotone property of ψ,we have Case 2ThenBy using the strongly monotone property of ψ and the triangular inequality,we haveIt follows thatd(w1,y2n). Case 3Also we can obtain that By a similar argument to the above,we can obtain In view of(3.16)and(3.17),{d(w1,yn)}is a monotonic decreasing sequence.From the lemma3.1,{d(w1,yn)}is convergent to either r=θ or r∈intP. From(3.14)and(3.15),there is a sequence{nk}of positive integer numbers with nk Case 1for k=1,2,···.ThenBy taking k → ∞ and using the properties of ψ and ϕ,we get ψ(r)≤ ψ(r)−ϕ(r).Hence ϕ(r)= θ and so r= θ. Case 2for k=1,2,···.By the triangular inequality, By taking k → ∞,we get ψ(r)≤ ψ(r)− ϕ(r).Hence ϕ(r)= θ,and so r= θ. Case 3.for k=1,2,···.Then Clearly,also we have r=θ.Therefore, as n→∞.By a similar argument to the above,we can obtain that as n→∞.Now,by using the triangular inequality,we have where n=1,2,···.By taking n → ∞ in the inequality above and using(3.18),(3.19),we obtain d(w1,w2)=θ and so w1=w2. [1]ALBER Y,GIERRE-DE ABROERS S.Principles of weakly contractive maps in Hilbert spaces[J].Oper Theory Adv Appl,1997,98:7-22. [2]RHOADES B E.Some theorems on weakly contractive maps[J].Nonlinear Anal,2001,47(4):2683-2693. [3]KHAN M S,SWALEH M,SESSA S.Fixed point theorems by altering distances between the points[J].Bull Austral Math Soc,1984,30(1):1-9. [4]BEG I,ABBAS M.Coincidence point and invariant approximation for mappings satisfying generalized weak contractive condition[J].Fixed Point Theory Appl,2006,2006:1-7.ArticleID74503. [5]ZHANG Qing-nian,SONG Yi-sheng.Fixed point theory for generalized ϕ-weak contractions[J].Appl Math Lett,2009,22:75-78. [6]DORIĆ D.Common fixed point for generalized(ψ,ϕ)-weak contractions[J].Appl Math Lett,2009,22:1896-1900. [7]ABBAS M,DORIĆ D.Common fixed point theorem for four mappings satisfying generalized weak contractive condition[J].Faculty of Sciences and Math Uni of Niŝ Serbia Filomat,2010,24(2):1-10. [8]JUNGCK G.Common fixed points for noncontinuous nonself maps on non-metric spaces[J].Far East J Math Sci,1996,4:199-215. [9]ABBAS M,NAZIR T,RADENOVIĆ S.Common fixed points of four maps in partially ordered metric spaces[J].Appl Math Lett,2011,24(9):1520-1526,dOi:10.1016/j.aml.2011.03.038. [10]ESMAILY J,VAEZPOUR S M,RHOADES B E.Coincidence point theorem for gneralized weakly contractions in ordered metric spaces[J].Appl Math Comput,2012,219:1536-1548. [11]ESMAILY J,VAEZPOUR S M,RHOADES B E.Coincidence and common fixed point theorems for a sequence of mappings in ordered metric spaces[J].Appl Math Comput,2013,219(10):5684-5692. [12]SHATANAWI W,SAMET B.On(ψ,ϕ)-weakly contractive condition in partially ordered metric spaces[J].Comput Math Appl,2011,62:3204-3214. [13]HUANG Long-guang,ZHANG Xian.Cone metric spaces and fixed point theorems of contractive mappings[J].J Math Anal Appl,2007,332:1468-1476. [14]HAN Yan,XU Wang-bin,XU Shao-yuan.Some new theorems of Lipshitz type mappings in cone metric spaces[J].Chin Quart J of Math,2013,28(2):224-233. [15]CHOUDHURY B S,METIYA N.The point of coincidence and common fixed point for a pair of mappings in cone metric spaces[J].Comput Math Appl,2010,60:1686-1695. [16]CHOUNDHURY B S,METIYA N.Fixed point and common fixed point results in ordered cone metric spaces[J].An St Univ Ovidius Constanta,2012,20(1):55-72. [17]NASHINE H K,SAMET B,KIM J K.Fixed point results for contractions involving generalized altering distances in ordered metric spaces[J].Fixed Point Theory Appl,2011,2011(5):http://dx.doi.org/10.1186/1687-1812-2011-5. [18]JUNGCK G,RHOADES B E.Fixed point for set valued function without continuity[J].Indian J Pure Appl Math,1998,29(3):227-238.§3. Main Results







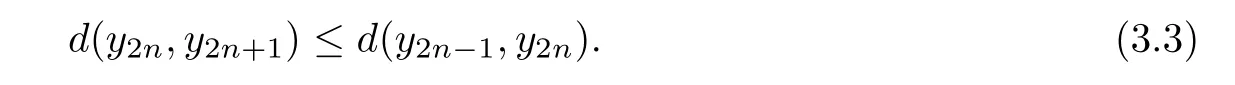


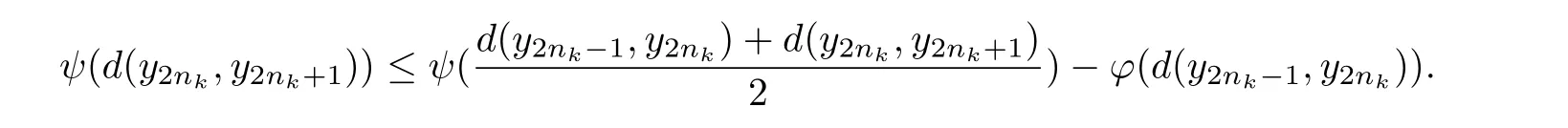




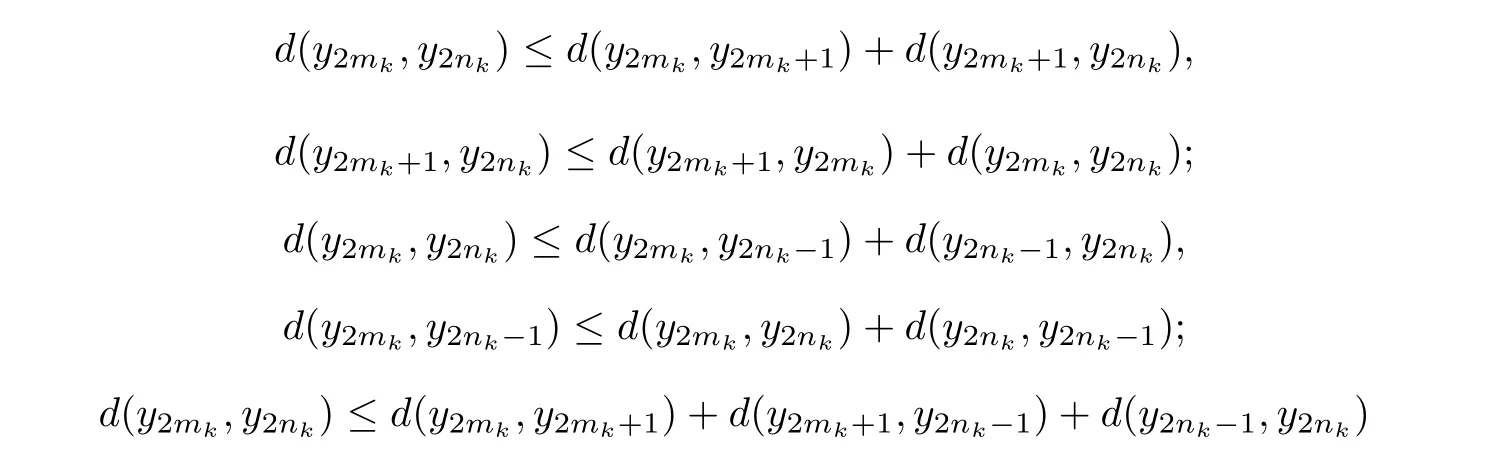





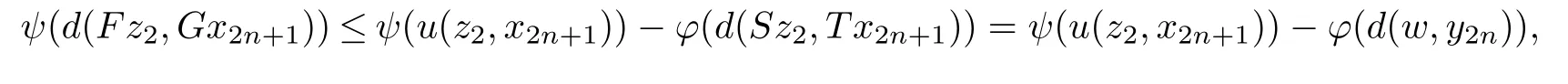
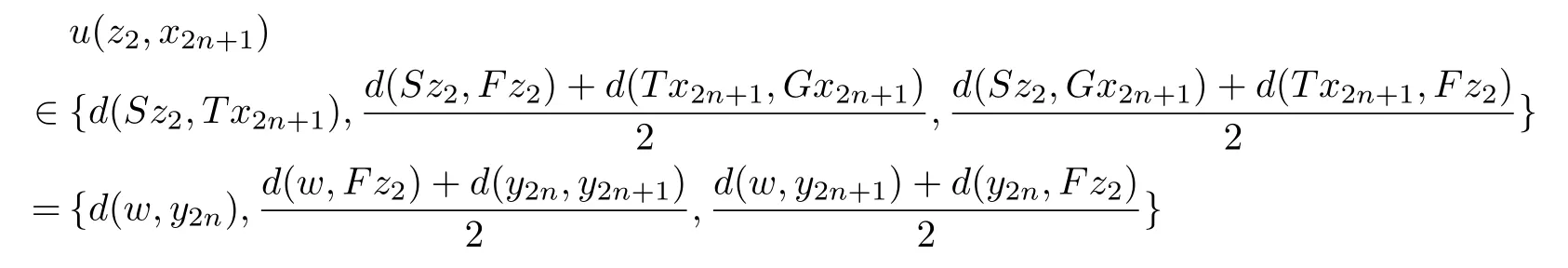





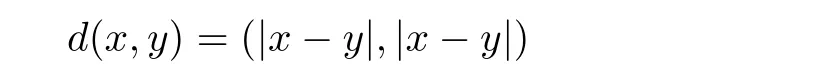



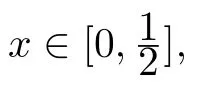




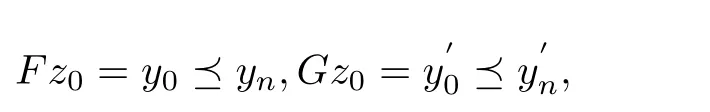








猜你喜欢
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Some Generalized Normal Subgroups and p-nilpotency of Finite Groups
- The Growth Order of Solutions of Systems Complex Di ff erence Equations
- The{P,k+1}-re flexive Solution to System of Matrix Equations AX=C,XB=D
- The Credibility Estimators under MLINEX Loss Function
- Implicative Pseudo Valuations on Hoops
- An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
