The Growth Order of Solutions of Systems Complex Di ff erence Equations
2018-07-06
(School of Mathematics and Statistics,Guangdong finance and Economics University,510320)
§1. Introduction
We use the standard notation of the Nevanlinna theory of meromorphic functions(See,for example,[1,2]).Speci fically,we denote the convergence exponent of the zeros of f(z)by λ(f),the convergence exponent of the poles of f(z)by,and the order by ρ(f).
Let c be a fixed non-zero complex number,

for each integer n>2.The paper make clear which quantity is under discussion.Equations written with the above di ff erence operatorsare di ff erence equations.Let E be a subset on the positive real axis.We de fine the logarithmic measure of E to be

A set E∈(1,+∞)is said to have finite logarithmic measure if log(E)<∞
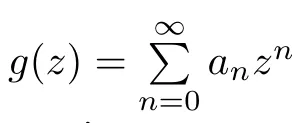

Some authors investigated the problem of the solutions of the growth of an entire or meromorphic solution of a nonlinear algebraic di ff erential equation of the form

where I is a finite set of multi-indices(i0,i1,···in)=(i),and they obtain some results(see[3-10]).
In 2010,Gao Ling-yun in the article[11]investigated the problem of the growth of solution of system of complex di ff erential equations of the form

which

He obtained


Then

§2.The Main Result of This Paper
The purpose of this article is to study the problem of growth order of solutions of a type of systems of di ff erence equations of the from

Then,
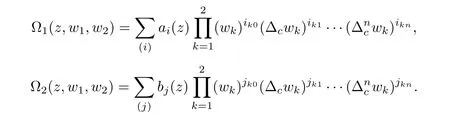
{ai(z)},{bj(z)},a(z),and b(z)are polynomials,
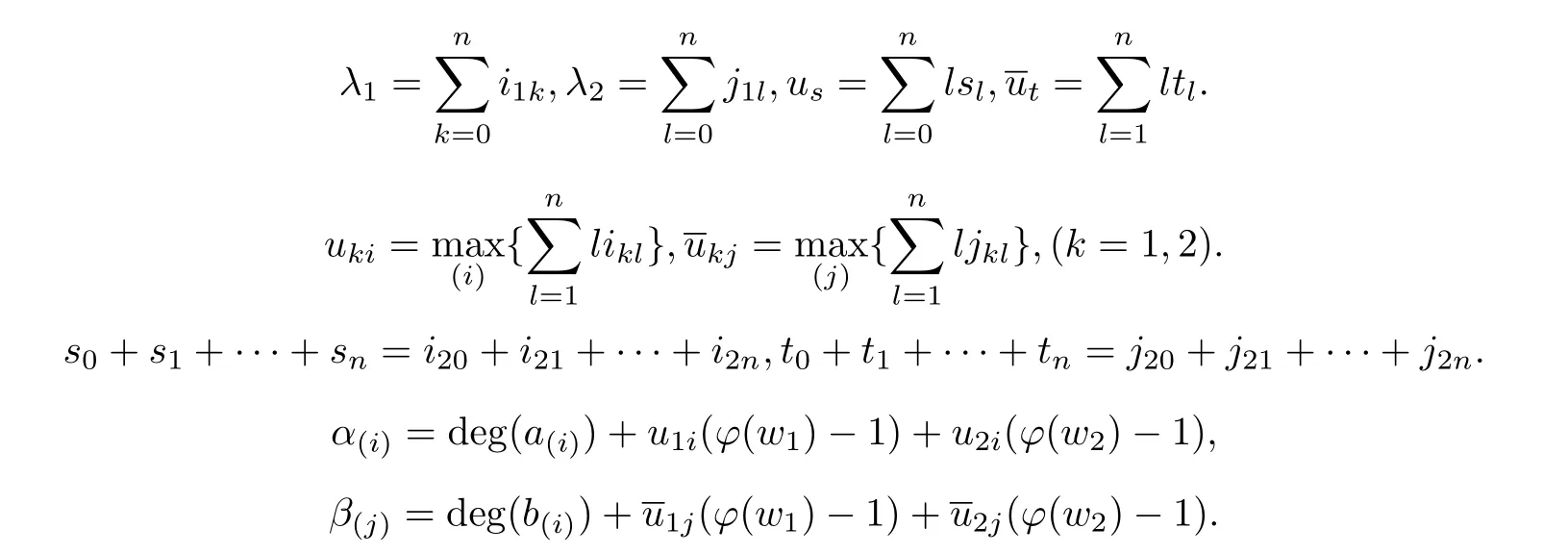
Theorem 2.1Let(w1(z),w2(z))be a transcendental entire solution of(2.1),Ωi(z,w1,w2)(i=1,2)be homogeneous on.If one of the following conditions is satis fied:
(1)
(2)then among ϕ(w1)≥ 1,ϕ(w2)≥ 1,at least one of them will be true.
§3.Some Lemmas
Lemma 3.1[1]Ifis an entire function of order ρ(f),then,

Lemma 3.2[10]Let f(z)be a transcendental entire function of order ρ = ρ(f)<1,and η be a fixed,non-zero number;letand z be such that|z|=r,where

if 0<ρ<1,then

where
Lemma 3.3[10]Let f(z)be a meromorphic function of order ρ = ρ(f)<1,Then,for each given ε>0,and integers 0≤ j Lemma 3.4[9]Let f and h be monotone non-decreasing function on[0,∞)such that g(r) ≤ h(r),for alwhere E ⊂ (1,∞)is a set of finite logarithmic measure.Let α >1 be a given constant.Then,there exists an r0=r0(α)>0 such that g(r)≤ h(αr)for all r ≥ r0. Let(w1(z),w2(z))be a transcendental entire solution of(2.1)with order ρ(w1,w2)<1,By Lemma 3.1, We prove that for each δ>0,there exists a sequence rn→ ∞,such that rn+1>De fine which is a union of non-intersecting intervals and clearly has in finite logarithmic measure.We consider all those r that lie in,Then,as v(r,wi)is a non-decreasing function of r,we have We choose δ and ε,so small that the inequality holds,where.Hence, By Lemma 3.2 and taking η=1,we obtain We rewrite(2.1)as follows: By Lemma 3.3 and(4.1),we choose r and r=|z|6∈F so big that the inequality Then we can obtain By Lemma 3.4 and(4.4),we can get where ε1,ε2>0 are arbitrarily small numbers. So Combining(4.6)and(4.5),we obtain Asthen, Similarly,we have By(4.7)and ϕ(w1)<1,we obtain So By(4.8)and ϕ(w2)<1,we obtain It is in contradiction with the conditions in Theorem 2.1. Example 1The system of complex di ff erence equations of the form then(w1,w2)=(z,z2)is a solution of the system of complex di ff erence equations of the form,and ρ(w1)=0,ρ(w2)=0. So ·[3−3]+2·[3−7]= −8<0. In this case,It shows that the conditions in Theorem 2.1 is right. Example 2The system of complex di ff erence equations of the form then(w1,w2)=(z2,ez)is a solution of the system of complex di ff erence equations of the form(2.1),and ρ(w1)=0,ρ(w2)=1. ·[3−4]+1·[2−2]= −1<0. In this case,the lower bound in Theorem 2.1 can be reached. [1]YI Hong-xun,CC YANG.Theory of the uniqueness of meromorphic functions(in Chinese).Beijing:Science Press,1995. [2]I LAINE.Nevanlinna Theory and Complex Di ff erential Equations,Walter de Gruyter,Berlin,1993. [3]HE Yu-zan,XIAO Xiu-zhi.Algebroid functions and ordinary di ff erential equation(in Chinese).Beijing;Science Press.1988. [4]GOLDBERG A A.On single-valued solutions of algebraic di ff erential equations.Ukrain Mat Zh,1956,8:245-261. [5]HAYMAN W K.The growth of solutions of algebraic di ff erential equations Rend Mat Acc Lincei,1996,7:67-73. [6]KORHONEN R.Meromorphic solutioins of di ff erential and di ff erence equatioins with de ficiencies[PH D Thesis].Helsinki:Ann Acad Sci Fenn,2002:129.J.of Math,2003,23(3):383-384. [7]GAO Ling-yun.On admissible solutions of two types of systems of di ff erential equa-tions.Acta Math Sinica(in Chinese),2000,43(1):149-156. [8]BERGWEILER W.On a theorem of Goldberg concerning meromorphic solutions of a-lgebraic di ff erential equations.Complex Variables,1998,37:93-96. [9]GUNDERSEN G.Finite order solutions of second order linear di ff erential equations.Trans Amer Math Soc,1988,305(1):415-429. [10]Y M CHIANG,S J FENG.On the growth of logarithmic di ff erence quotients and logarithmic derivatives of meromorphic functions.Trans Amer Math Soc,2009,361:3767-3791. [11]GAO Ling-yun.The growth of solutions of systems of complex nonlinear algebraic di ff erential equations.Acta Mathematica Scientia.2010,30B(3):932-938.
§4.The Main Result of This Paper

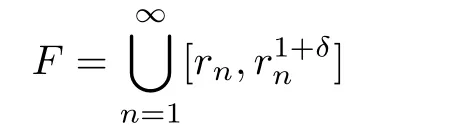
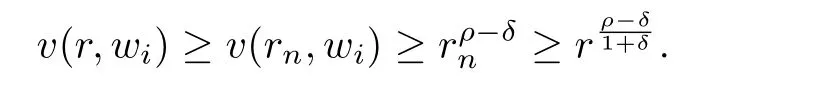


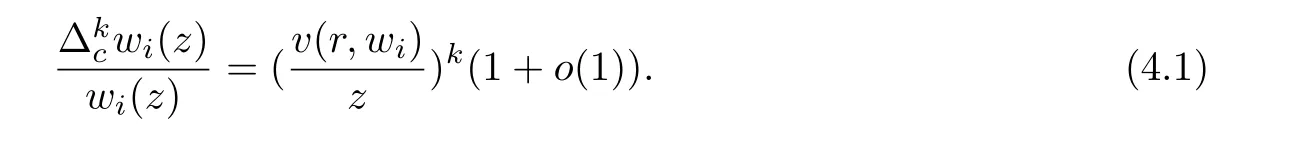




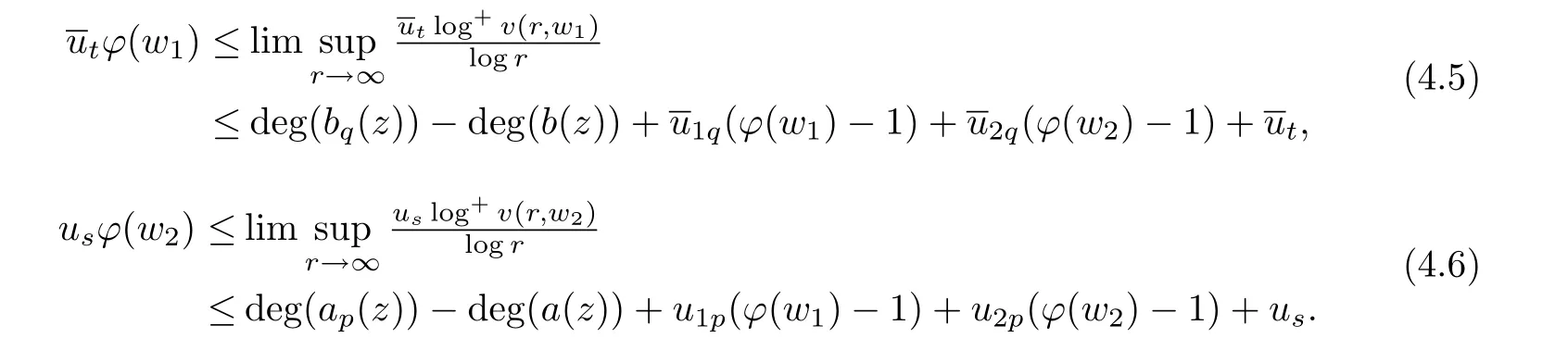

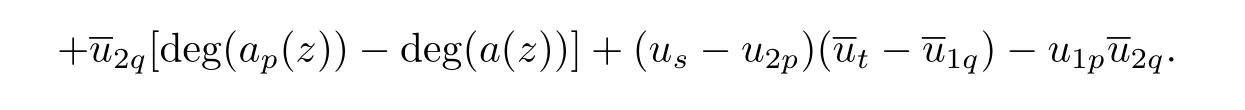

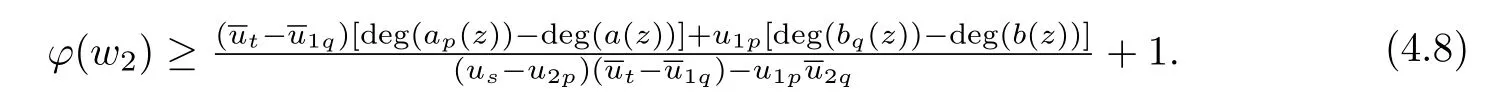
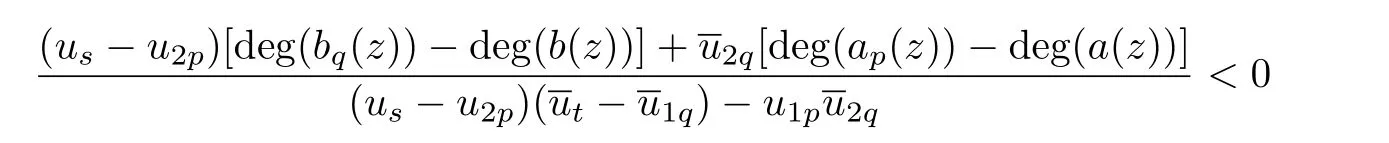

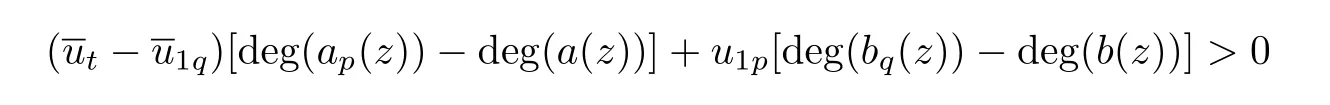
§5.Examples 1
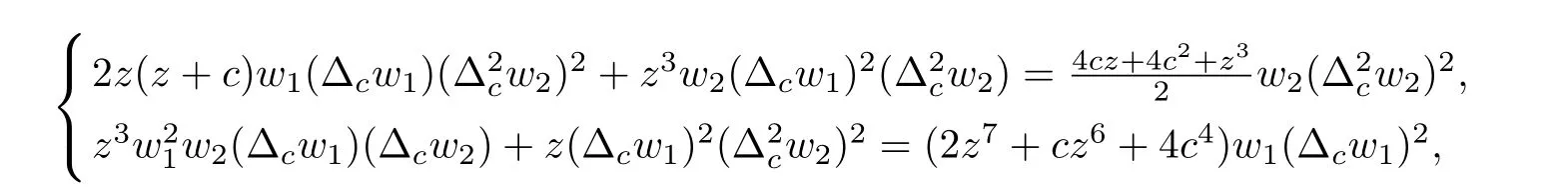




杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Common Fixed Point Results for Quasi-contractions Involving Altering Distance Functions in Ordered Cone Metric Spaces
- Some Generalized Normal Subgroups and p-nilpotency of Finite Groups
- The{P,k+1}-re flexive Solution to System of Matrix Equations AX=C,XB=D
- The Credibility Estimators under MLINEX Loss Function
- Implicative Pseudo Valuations on Hoops
- An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
