新型随钻取心钻头破岩提速工作机理

田家林 朱 志 程文明 杨 琳

1. 西南石油大学机电工程学院 2.西南交通大学机械工程学院

钻井过程中的随钻取心在可实现对地质参数准确记录的同时，还能够：①根据得到的钻进地层岩性参数，优化相关层位的钻具设计，包括钻头的个性化设计，以及提速或减摩工具的优化组合，实现钻井过程提速增效，节约生产成本、降低井下事故风险；②为后期的油气资源开发、增产增效提供重要的基础数据与参考依据[1-5]。基于研究现状，笔者设计出一种全新的随钻取心钻头，与现有技术不同，通过在钻头体内部设置一个回旋通道，当钻井液流经此通道时，由于空化效应，会对通道下部的岩心形成吸附效应，而对于上部岩屑会产生推送效果。基于流体动力学理论和岩石破坏力学，建立了随钻取心钻头工作机理分析模型，对钻井过程中岩石破碎和机械钻速的计算方法进行了研究。通过比较现场实验数据，发现新型随钻取心钻头在保证岩心取样规整的同时，内部通道的吸附效应会使钻头中心岩石的承压情况发生变化，而大幅度增加岩石可钻性，对于破岩提速有重要的积极意义。

1 新型随钻取心钻头设计

首先分析现有随钻取心钻头的结构与破岩特点，如图1所示两种典型的随钻取心钻头。实际钻井工程中，由于钻头钻进的复合运动，图1-a所示的随钻取心钻头钻井过程中的岩心有可能在通道处产生拥堵，当然随着钻井破岩进一步作业，会继续增加岩心环空挤压力，以及优化此处的水眼设计与刀翼倾斜角度，可减轻或避免此种情况。但由于堵塞情况存在的可能性，实际钻井过程中，由于钻井液、岩心、岩屑、钻头、井壁的耦合关系，有可能产生岩心的重复破碎，影响取心效果，或者由于岩屑的重复破碎，降低钻井破岩效率[6-10]。

图1 现有的两种随钻取心钻头图

与此对应，图1-b所示的随钻取心钻头，由于在钻头内部有专用通道，在离井底较远处，岩心从通道中被挤出，进入环空，可避免第1种设计中所述的问题，或者在其他条件相同的情况下，对于保持岩心的完整性、避免岩屑重复破碎有积极意义，对于钻井破岩提速增效有实际效果。但是，由于岩心从专用通道流出，所以设计中必须保证在钻井条件下，岩心不会在通道发生堵塞，即岩心被往上挤压的过程中，一定不能产生“锁死”现象，为避免这种现象，需要考虑岩心形状、通道结构尺寸、岩心与通道的接触、摩擦等情况[11-14]。

在充分考虑现有设计方法、研究现状的基础上，本文提出一种全新的随钻取心钻头，如图2所示。通过在钻头内部设计一个射流专用通道（以下简称专用通道），钻头内部的高压钻井液不通过钻头喷嘴到环空，而从专用通道以速度v0经射流喷嘴流出，同时在负压作用下吸附通道以流速vs携带岩心进入推送通道，然后以流速vc与所取岩心回到环空。

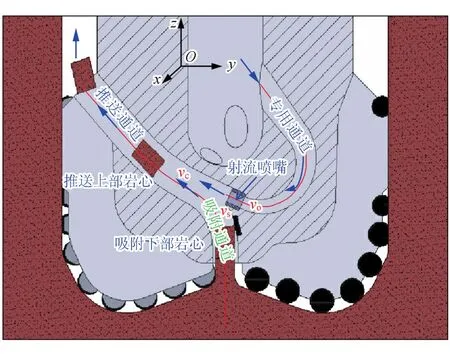
图2 新型随钻取心钻头设计示意图

由于钻头内部的钻井液压力较高，以及根据流体动力学计算模型，当钻井液进入专用通道直至从环空流出的过程中，在钻头中心处由于负压效应，会对下部的岩心产生吸附作用，而对位于推送通道中的岩心，又会有推送效果。即破岩过程中，由于专用通道的存在，结合实际钻井工作情况，新设计的随钻取心钻头会对岩产生“吸附下部岩屑，推送上部岩屑”的效果。

这样的设计对于破岩性能的影响包括两个方面，首先可使推送通道保持畅通，取心的岩样比较均匀，避免了岩心掉落后的重复破碎。另一方面，新设计的随钻取心钻头（下文简称新钻头）同时会改变井眼中心的围压分布，导致心部岩石可钻性大幅度提高，进而提高钻头机械钻速。

2 工作机理分析模型

新钻头的工作机理研究包括通道中的钻井液动力学分析，以及其对岩石受压状态的影响，进而得到新条件下的岩石破碎计算模型，在此基础上，可得到的重要结果包括新钻头的破岩特性以及机械钻速计算结果。

2.1 流体动力特性

首先进行新钻头的流体动力学计算，得到不同流量、压力的钻井液条件下，钻井液流经专用通道后，其压力分布结果，可为“吸附下部岩屑、推送上部岩屑”量化分析提供理论基础。结合井下实际工作情况，可得钻井液的关键因素包括介质密度、压力、流量、黏度、温度等关键参数，再根据钻进过程钻头处的特殊工况，重点对钻井液压力、流量进行分析。

2.1.1 稳定流动流量分配方法

建立专用通道射流喷嘴吸附下部岩屑模型，首先需要计算钻井液在钻头处对应钻头喷嘴、取心专用通道的结构时，其流量分配的计算，根据井底实际工作情况参数，利用稳定流动流量分配方法[15-17]：

式中 表示分析对象所占总流量的比例；R、Ri分别表示总体与分析对象的流阻，Pa·s/m2；Li表示分析管长，m。

当雷诺数2 300＜Re＜4 000时，管道中的流体流动为过渡状态，Re＞4 000时，流体流动为湍流，摩擦系数表达式为：

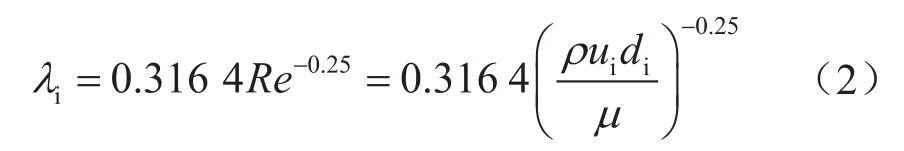
式中ρ表示流体的密度，kg/m3；ui表示流体速度，m/s；μ表示黏性系数，Poise；di表示特征长度，对应专用通道，表示通道的当量直径，m。

结合流动的摩阻计算公式：

得到流体流阻的计算公式为：

将此运动状态等效折合为相同流阻条件下的层流流动，该流动状态的流阻为：

根据系统流阻条件进而可以得到：

式中Δp表示通道阻力，即压差，Pa；Li表示通道长度，m；Vi表示体积流量，m3/s。

将公式（6）带入公式（1），且利用计算机编程进行迭代，则可得到湍流管道的流量分配比例，确定进入专用通道的钻井液流量。

2.1.2 喷嘴处的压降计算

根据前面所述，文章核心在于对底部岩心的吸附，以及对于上部岩屑的推送效果。而下部的吸附是由于负压效应所引起的，根据流体动力学理论，得到对于底部吸附效果的计算方法。进行随钻取心钻头的通道压力计算，需要考虑两个方面的因素：①专用通道至取心通道处的喷嘴对流体压力的改变，②基于流体动力学的吸附效应的计算分析。喷嘴处的压降[9]表示为：

式中Δpb表示喷嘴处的压降，MPa；ρd表示喷嘴喷出的流体密度，kg/m3；C表示喷嘴流量系数，无因次，表示喷嘴的阻力系数；Q表示喷嘴处流量，m3/s；A0表示喷嘴面积，m2。

2.1.3 射流结构对底部岩心的吸附效应

在确定射流喷嘴流出的钻井液压力、流量基础上，可计算射流结构对底部岩心的吸附效应，首先将钻井液作不可压缩流体，其基本方程组为[18]：

连续性方程

运动方程

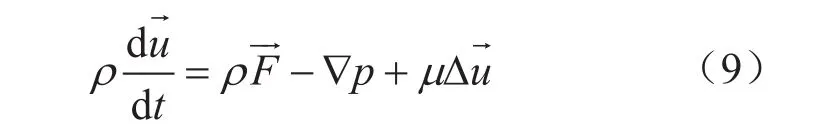
能量方程

式中 表示哈密顿算子； 表示速度矢量，m/s；ρ表示流体的密度，kg/m3；p表示流体压力，Pa；表示质量力，N；μ表示动力黏性系数，Pa·s；cp表示流体的定压热容，J/（mol·K）； 表示流体运动参数，无因次；T表示温度，K；k表示流体热传系数，W/（m2·K）；q表示流体热量，J。

进行专用通道喷嘴对下部岩屑的吸附效果计算，集中在其对于下部产生的负压效应分析。首先确定吸附通道和专用通道流量的比为：

式中Qs表示被吸入流体体积流量，L/s；Q0表示工作流体体积流量，L/s。

同理，得到推送通道和专用通道的压力比为：

式中Δpc、Δp0分别表示推送通道和吸附通道的压差、专用通道喷嘴处和吸附通道的压差，Pa；g表示重力加速度，m/s²；v0、vs、vc分别表示喷嘴流体位置、被吸流体位置、混合流体位置断面的平均速度，m/s；z0、zs、zc分别表示喷嘴流体位置、被吸流体位置、混合流体位置的位置水头，m；p0、ps、pc分别表示喷嘴流体位置、被吸流体位置、混合流体位置的压力，Pa；ρ0、ρs、ρc分别表示专用通道、吸附通道、推送通道流体的密度，kg/m3。

对于压力与速度场的求解，采用k-ε双方程紊流模型，其流动控制方程为以下表达形式：

将控制方程无量纲化，其连续性方程：

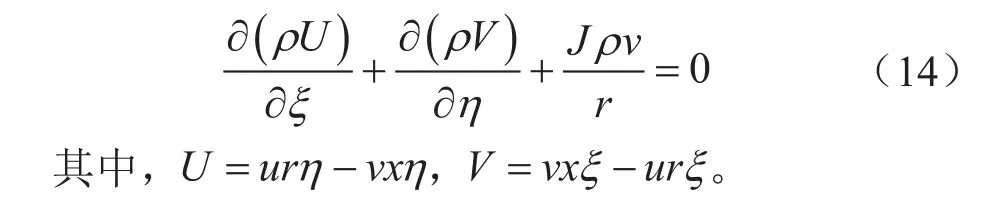
其动量方程：

进而可求解得到速度场与压力场。

对于射流的吸附效应计算，基于稳态解的广义Reynolds方程，根据分析模型中的坐标关系，得到y

方向零吸附工况下的Reynolds方程：

其中 的定义公式为：

根据黏性流体的伯努利方程：

式中α1、α2分别表示动能修正系数，无因次；hw表示黏性流体扬程损失，m。

由此得到Reynolds方程的边界条件为：

2.1.4 推送岩心效应

由于新钻头的结构特点，专用通道的喷嘴射流对下部吸附通道岩屑的吸附效应，以及对推送通道岩屑的推送效应，可减小或避免岩屑的重复破碎，所以需要考虑新钻头推送通道的携岩能力。考虑井身结构可能为直井或者水平井，根据井底实际工作情况，此处对岩心的作用考虑推送效应，建立分析计算方法为：

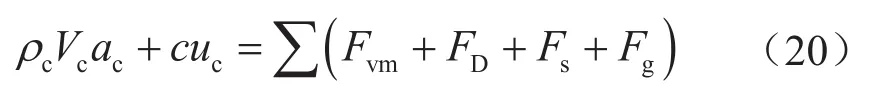
式中 ρc表示岩心密度，kg/m3；Vc表示岩心体积，m3；ac表示岩心加速度，m/s2；c表示阻力系数，N·s/m；uc表示岩心运移速度，m/s；Fvm、FD、Fs、Fg分别表示虚拟质量力、运动阻力、流体速度梯度力、重力（含浮力），N；推送过程中的各力计算方法分别如下：

虚拟质量力是由于岩心在液体中做加速运动时，速度越大，推动流体动能增加所产生的力将大于使岩心加速的力mcac，其效应等价于岩心的质量增加，计算公式为：

式中km表示经验系数，无因次；uf表示流体速度，m/s；dt表示t时刻速度曲率半径，m。

运动阻力的计算方法如下：

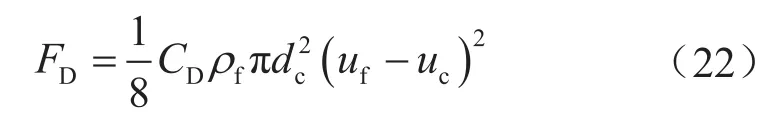
式中CD表示阻力系数，其与颗粒雷诺系数有关，无因次；ρf表示流体密度，kg/m3；dc表示岩心有效直径。

同时修正得到不同流动工况下的摩擦阻力计算公式：

式中表示修正系数，无因次； 是与物性参数、流动参数、几何参数相关的函数；a、b、c表示特定参数，无因次；XTT表示Lockhart-Martinelli参数，表示两相摩擦倍率。

流体速度在y方向的梯度力计算方法如下：

该公式仅对于Re＜1有效，因为在流动的主流区，速度梯度通常都很小，故此时可忽略其影响，仅仅在速度边界层中，对于小尺寸的岩心，其作用才变得明显。

重力（含浮力）的计算方法如下：

式中lc表示岩心有效长度，m。

2.2 机械钻速计算

对于机械钻速的计算分析，机械钻速影响因素众多，对此本文研究基于以下内容展开，首先由于所述专用通道产生的负压效应对岩石围压的影响，导致岩石可钻性发生变化，会降低单位体积岩石有效破碎功，减小岩石破碎所需功耗[19-23]；其次是在实际钻井过程中，新钻头设计的专用通道在具有吸附下部岩屑，以及推送通道推送上部岩屑效果的同时，会增强了钻头排屑效果，减小了岩石重复破碎，提高了破岩效率。从而对于钻头破岩过程岩石破碎功、破岩效率产生影响。

考虑到钻井过程井下的复杂工况，结合本文研究的机械钻速影响因素，首先引入通用幂指数模式分析钻进过程的机械钻速：

式中Rate表示机械钻速，m/h；K表示系数，与可钻性相关，无因次；W表示钻压，N；N表示转速，r/min；Eb表示比水功率，kW/cm2；当Eb＞0.32 kW/cm2时，可认为井底清洁状态下破岩；e表示自然对数，无因次；Δp表示井底压差，Pa；C2表示切削齿磨损系数，无因次；h表示切削齿磨损量，mm；a、b、c、d分别表示钻压指数、转速指数、水功率指数和压差指数；并且，计算公式中的系数K、a、b、c、Eb可根据岩性参数查相关手册确定取值范围，然后利用计算机编程进行迭代计算，确定最终结果。

如前所述，由于新钻头对井底岩心的吸附效应，以及对于重复破碎率的影响，在现有的机械钻速计算的基础上，得到新的机械钻速计算公式：

式中M0表示保证井底清洁时的临界比水功率时的门限钻压，N；We表示水力作用的当量钻压，N。

考虑到实际钻井工程中的具体情况，当其他因素不变时，机械钻速与钻头射流比水功率的关系为：

式中R0-ate表示单纯依靠机械破岩的钻速，m/h；rate表示水力因素产生的钻速增量，m/h。

由此可得W与Eb的关系为线性关系，将机械钻速公式改写为：

式中Ce表示射流水功率与当量钻压换算的系数，即比水功率转换率，无因次。当岩石可钻性介于3.13～9.98时，Ce取值范围介于0.217 8～0.012 4。

由于比水功率转换率与可钻性可用一元幂指数回归：

式中ω、λ分别表示比水功率与可钻性的相关系数与指数，无因次；由此得到修正后的机械钻速计算公式：

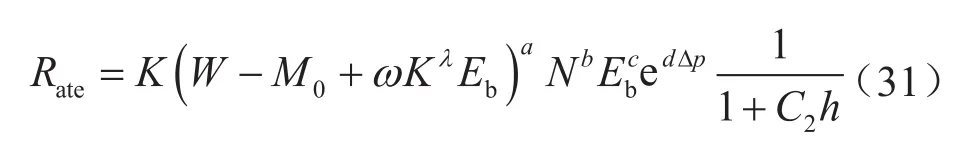
对于台架实验，由于采用新钻头，不考虑钻头磨损，同时不存在压差影响，式（31）简化为：

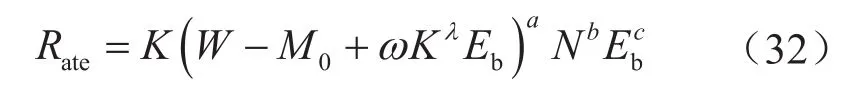
此计算方法与其他方法相比，与实际情况吻合度更高，考虑因素更全面，计算精度更高。

3 算例分析

为了对新钻头破岩特性进行量化分析，利用建立的理论模型，进行算例求解。分别计算其工作过程的液力分布，以及其他参数结果，确定关键参数对新钻头破岩性能的影响。利用钻头破岩模型，分析对钻头机械钻速的影响，得到新钻头对于破岩提速的实际意义。算例参数基础数据如表1所示。

表1 算例参数表

对于专用通道喷嘴而言，其当量尺寸变化对于其流量分配的影响如图3所示，由图3可知，随着喷嘴当量尺寸增加，流量增加幅度斜率减小，呈现非线性特性。

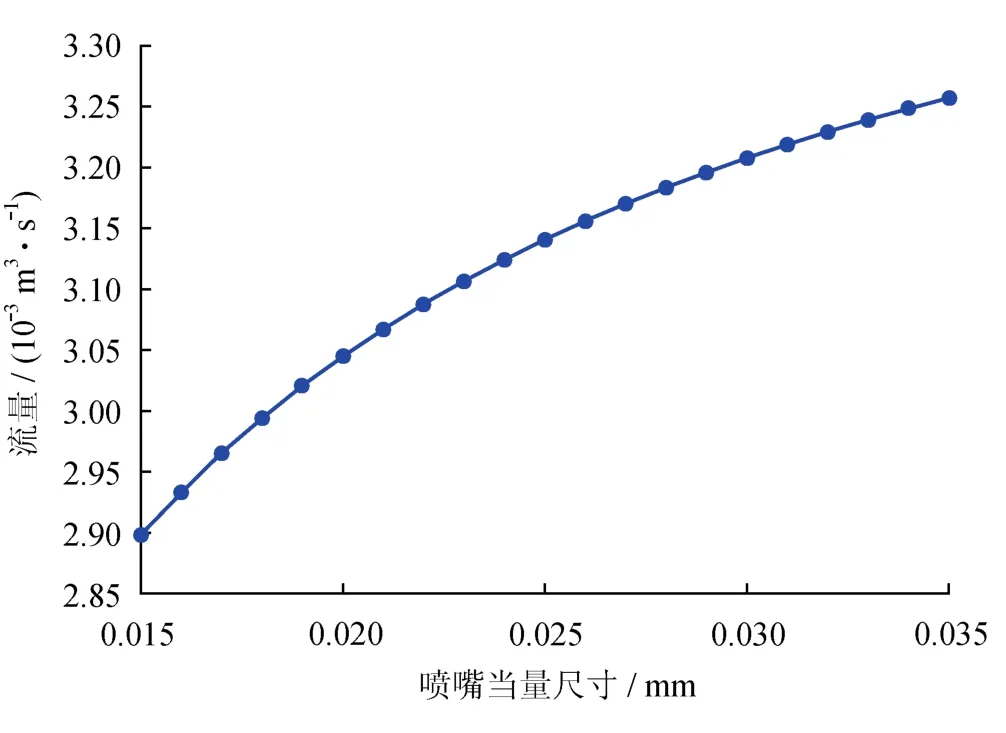
图3 喷嘴当量尺寸与流量的关系图

各喷嘴的压降、流量以及携带的最大颗粒见图4。

图4 各喷嘴的压降、流量及携带最大颗粒图

由图4可知，对于专用通道喷嘴（6号喷嘴）而言，其压降值远大于其他喷嘴，达到7 MPa以上；同时，其喷口处流体速度也远大于其他喷嘴，达到15 m/s以上。根据得到的水力参数结果计算得到的携带最大颗粒直径，专用通道喷嘴对应的岩屑直径达到35 mm以上，这里需要注意的是，此处的结果是根据喷口处的水力参数计算得到的，实际上由于井底情况复杂，影响因素众多，需要考虑其余喷嘴液力参数，以及岩石特性，才与环空返回的实际情况更接近。

为了对破岩性能进行更直观的对比，进行破岩分析的算例参数与后面实验相对应，在后面的台架试验、现场实验中，给出对应输入参数的计算结果与实验结果，并完成相关分析。

4 实验与分析

为验证理论模型，利用台架实验与现场实验对新钻头进行测试分析，将测试结果与理论结果进行对比分析，深化对新设计的随钻取心钻头破岩性能的理解。首先根据理论分析结果，进行与算例参数对应的实验钻头的加工，然后利用台架进行新钻头的实验，分析测试得到的岩心现状、破岩行为等特性。实验用的钻头参数与算例中的输入值相同，台架实验采用清水做钻井液，基础参数如表2所示。实验用钻头如图5所示，台架实验过程与井底模型如图6所示，为对比破岩性能，将同尺寸的其他类型随钻取心钻头进行相同条件实验，对破岩结果进行对比分析。

表2 台架实验参数表

实验得到的现有钻头、新钻头破岩过程机械钻速结果，并将两种随钻取心钻头的机械钻速结果处理，得到新钻头机械钻速增加比如图7所示。

由图7可知，其值大致分布区间介于3%～5%，室内实验取得了一定的提速效果，根据利用大排量泵的实验结果对比分析得到：产生这样的原因是由于台架试验钻井液排量太小，导致新设计所具备的“吸附下部岩屑、推送上部岩屑”的作用不明显。

图5 实验测试所用的新型随钻取心钻头图

图6 随钻取心钻头台架实验与结果照片

图7 新钻头机械钻速增加比值图

为进一步验证破岩性能、机械钻速结果，进行现场实验，同样采用与算例分析、台架实验相同的随钻取心钻头，且与其邻井使用其他钻头进行破岩效率对比。现场钻具组合参数为：Ø215.9 mmPDC×0.32 m＋ Ø172 mm螺杆×7.97 m＋回压凡尔×0.5 m＋Ø165.1 mm无磁钻铤（1根）×9.32 m＋ Ø215 mm扶正器1.07 m＋ Ø165.1 mm钻铤（14根）×128.6 m＋ Ø165.1 mm随钻震击器×9.56 m＋ Ø165.1 mm钻铤（3根）×26.92 m＋ Ø127 mm钻杆（加3只防磨接头），现场实验参数如表3所示。

表3 现场实验参数

由于钻井泵排量相对于室内实验大幅度增加，使新钻头的减小重复破碎能力，导致新钻头的增速效果很明显，在相同井段、相近钻井参数条件下进行机械钻速对比，可获得机械钻速增加比大致在5%～40%。

5 结论

1）提出的新型随钻取心钻头，与现有取心钻头不同，通过在钻头内部建立一个专用通道，钻头内部的高压钻井液流经专用通道至推送通道，然后至环空。通过结合井下情况，利用流体动力学、破岩力学，建立随钻取心钻头工作机理研究的理论模型，为进行新钻头破岩过程的“吸附下部岩屑、推送上部岩屑”，以及提速增效的特性，提供了理论支撑。

2）通过算例分析、台架实验与现场实验，对随钻取心钻头的关键参数以及提速效果进行了分析，且对比了不同类型钻头、计算方法的结果，对影响破岩性能的因素进行了确定，并给出了计算结果。研究结果表明，在现场条件下，钻井泵的排量、功率对钻头的提速效果影响较大，在钻井液流量为25 L/s的现场实验中，新钻头提速范围在5%～40%。

3）笔者提出的新型随钻取心钻头，经过实验室测试与现场实验，破岩性能与理论计算结果吻合，验证了理论模型的准确性与精度。同时，实验表明，新钻头的设计对于随钻取心技术发展，以及钻井过程提速增效，特别是对于大排量的钻井工程，进行提速技术研究具有重要的参考意义。

[ 1 ] Tian Jialin, Yang Yinglin & Yang Lin. Vibration characteristics analysis and experimental study of horizontal drill string with wellbore random friction force[J]. Archive of Applied Mechanics,2017, 87(9): 1439-1451.

[ 2 ] Tian Jialin, Li Jurui, Cheng Wenming, Zhu Zhi, Yang Lin, Yang Yi, et al. Working mechanism and rock-breaking characteristics of coring drill bit[J]. Journal of Petroleum Science and Engineering, 2018, 162: 348-357.

[ 3 ] Horsrud P. Estimating mechanical properties of shale from empirical correlations[J]. SPE Drilling & Completion, 2001, 16(2): 68-73.

[ 4 ] Tian Jialin, Liu Gang, Yang Lin, Wu Chunming, Yang Zhi & Yuan Changfu. The wear analysis model and rock-breaking mechanism of a new embedded polycrystalline diamond compact[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2017, 231(22): 4241-4249.

[ 5 ] Peyret R & Taylor TD. Computational methods for fl uid fl ow[M].Вerlin: Springer Science & Вusiness Media, 1983.

[ 6 ] Tian Jialin, Yang Zhi, Li You, Yang Lin, Wu Chunming, Liu Gang, et al. Vibration analysis of new drill string system with hydro-oscillator in horizontal well[J]. Journal of Mechanical Science and Technology, 2016, 30(6): 2443-2451.

[ 7 ] Ho LT, Cheung ВC, Kong Lingbao, & Ren Mingjun. Theoretical and experimental investigation of three-dimensional-structured surface generation using fl uid jet polishing[J]. Proceedings of the Institution of Mechanical Engineers, Part В: Journal of Engineering Manufacture, 2017, 231(13): 2317-2335.

[ 8 ] Tian Jialin, Yuan Changfu, Yang Lin, Wu Chunming, Liu Gang& Yang Zhi. The vibration analysis model of pipeline under the action of gas pressure pulsation coupling[J]. Engineering Failure Analysis, 2016, 66: 328-340.

[ 9 ] 朱劲木, 梁爱国, 龙新平. 射流泵性能的数值计算[J]. 武汉大学学报(工学版), 2002, 35(6): 7-10.Zhu Jinmu, Liang Aiguo & Long Xinping. Numerical calculation of performances of jet pump[J]. Engineering Journal of Wuhan University (Edition of Engineering), 2002, 35(6): 7-10.

[10] Tian Jialin, Yuan Changfu, Yang Lin, Fu Chuanhong, Liu Gang,Yang Zhi, et al. Rock-breaking analysis model of new drill bit with tornado-like bottomhole model[J]. Journal of Mechanical Science and Technology, 2015, 29(4): 1745-1752.

[11] Вeaucamp A, Namba Y & Freeman R. Dynamic multiphase modeling and optimization of fl uid jet polishing process[J]. CIRP Annals, 2012, 61(1): 315-318.

[12] Panciroli R & Porf i ri M. Evaluation of the pressure fi eld on a rigid body entering a quiescent fl uid through particle image velocimetry[J]. Experiments in Fluids, 2013, 54(12): 1630.

[13] Qiu Вinbin, Tang Si, Yan Junjie, Liu Jiping, Chong Daotong &Wu Xinzhuang. Experimental investigation on pressure oscillations caused by direct contact condensation of sonic steam jet[J].Experimental Thermal and Fluid Science, 2014, 52: 270-277.

[14] Lu Yiyu, Tang Jiren, Ge Zhaolong, Xia Вinwei & Liu Yong. Hard rock drilling technique with abrasive water jet assistance[J].International Journal of Rock Mechanics and Mining Sciences,2013, 60: 47-56.

[15] Liu Xiaohui, Liu Songyong & Ji Huifu. Numerical research on rock breaking performance of water jet based on SPH[J]. Powder Technology, 2015, 286: 181-192.

[16] Xu Lingchao, Guan Zhichuan & Li Jingjiao. Design and application of a rock breaking experimental device with rotary percussion[J]. Advances in Petroleum Exploration and Development,2016, 11(2): 16-20.

[17] Li Wai, Zhao Xionghu, Li Yufei, Ji Yihui, Peng Hui, Liu Lan, et al. Laboratory investigations on the eあects of surfactants on rate of penetration in rotary diamond drilling[J]. Journal of Petroleum Science and Engineering, 2015, 134: 114-122.

[18] Tang Jiren, Lu Yiyu, Ge Zhaolong, Xia Вinwei, Sun Huijuan &Du Peng. A new method of combined rock drilling[J]. International Journal of Mining Science and Technology, 2014, 24(1):1-6.

[19] 陈庭根, 管志川. 钻井工程理论与技术[M]. 东营: 中国石油大学出版社, 2000.Chen Tinggen & Guan Zhichuan. Drilling engineering theory and technology[M]. Dongying: China University of Petroleum Press,2000.

[20] Tien YM, Kuo MC & Juang CH. An experimental investigation of the failure mechanism of simulated transversely isotropic rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(8):1163-1181.

[21] 田家林, 庞小林, 梁政, 杨琳, 张亮. 旋风状井底模型的新型钻头运动特性[J]. 石油学报, 2013, 34(6): 1163-1167.Tian Jialin, Pang Xiaolin, Liang Zheng, Yang Lin & Zhang Liang. Kinematic features of a new drill bit of the tornado-like bottom-hole model[J]. Acta Petrolei Sinica, 2013, 34(6): 1163-1167.

[22] 赵吉坤, 张子明. 三维大理岩弹塑性损伤及细观破坏过程数值模拟[J]. 岩石力学与工程学报, 2008, 27(3): 487-494.Zhao Jikun & Zhang Ziming. 3D Numerical simulation of elastoplastic damage and microfracturacturing process of marble samples[J]. Chinese Journal of Rock Mechanics & Engineering,2008, 27(3): 487-494.

[23] 郑德帅, 高德利, 冯江鹏. 实钻条件下井底岩石可钻性预测模型研究[J]. 岩土力学, 2012, 33(3): 859-863.Zheng Deshuai, Gao Deli & Feng Jiangpeng. A model for downhole rock drillability prediction under real drilling condition[J].Rock & Soil Mechanics, 2012, 33(3): 859-863.