渭河流域宝鸡段气温及降水突变分析

，，

(浙江工业大学 建筑工程学院，浙江 杭州 310023)

渭河是宝鸡市的母亲河，是宝鸡市重要的农业灌溉水源和地下水重要补充水源，同时还担负泄洪、排污以及维护生态平衡的任务，对宝鸡市经济社会发展起到至关重要的作用[1].宝鸡市隶属渭河上游和中游段，流域面积1.329×104km2，全长224 km，自陈仓区凤阁岭镇进入宝鸡市，其干流自西向东至扶风县绛帐镇流出.渭河流域的河川径流主要靠降水补给，气候变化在一定程度上将改变水文循环的现状，从而引起水资源在时空上的重新分配，影响到降水、蒸发、径流和土壤湿度等水循环要素的时空分布，势必会影响到生态系统平衡和社会经济发展[2].

笔者选取渭河流域宝鸡段1956—2008 年气温和降水资料，采用累积距平法[3-4]、 Mann-Kendall检验法[5-8]、滑动T检验法[9-10]和Yamamoto法[11-13]对气温和降水的变化趋势进行突变分析，通过多种突变方法的综合分析来判断流域气温和降水的突变点，进而为该地区水资源评价提供科学的气候变化背景和研究方法.

1 数据来源

笔者采用的数据为渭河流域宝鸡段5 个气象站1956—2008 年日平均气温和日降水资料，来源于中国气象科学数据共享网.气温和降水数据取5 个站点的平均值并按月、四季、年及年际等进行整理，个别缺失的数据按照线性回归法进行插补；四季划分按3月至5月为春季，6月至8月为夏季，9月至11月为秋季，12月至翌年2月为冬季.

2 研究方法

2.1 Mann-Kendall趋势检验法

在时间序列趋势分析中,Mann-Kendall检验法是一种非参数检验方法，该检验方法不要求样本服从一定的分布，即使有少数异常值，检验结果也不会受到干扰，水文、气象等大多是非正态分布的数据，适合采用Mann-Kendall检验法对其变化趋势进行分析.

设气候序列为x1，x2，…，xn，秩序列Sk是第i个样本xi大于xj(1≤j≤i)的累计数，其计算式为

(1)

x1，x2，…，xn相互独立，且具有相同连续分布，累计数Sk的均值E(Sk)和方差var(Sk)计算式分别为

(2)

(3)

假定原序列是随机及独立的，将Sk标准化为

(4)

按x的逆序列xn，xn-1，…，x1，同样采用以上计算方法，同时使得：

(5)

式中：k=n，n-1，…，1；UB1=0.

根据统计序列UFk，UBk可以进一步分析序列的变化，而且可以识别突变的开始时间，明确突变的区间.若UFk>0，则说明序列表现出上升的趋势；UFk<0，说明序列表现出下降的趋势；当UFk超过临界线时，说明序列的上升或下降变化趋势较明显.如果UFk，UBk这两条曲线相交，而且交点在两条临界线之间，则可判断交点对应的时间点就是研究序列开始突变的时间点.

2.2 滑动T检验法与Yamatomo检验法

滑动T检验法是利用T检验法的原理，对序列逐点进行T检验.T检验法的原理：设滑动点为序列1，滑动点后为序列2，序列1和序列2的分布函数分别为F1(x)，F2(x)，从总体F1(x)，F2(x)中抽取样本，容量分别为n1和n2，对原假设F1(x)=F2(x)进行检验，则

(6)

其中

(7)

(8)

(9)

(10)

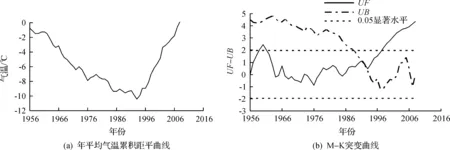
T服从t(n1+n2-2)分布，临界值tα/2根据t分布表得到：当T>tα/2时，原假设被拒绝，说明抽取的两个样本存在显著性差异；当T

Yamatomo检验方法基本原理与滑动T检验相同，它通过定义一个信噪比SNR来判断突变位置：当SNR>1.0时，认为有突变发生；当SNR>2.0时，则认为有强突变发生.

3 突变分析

3.1 累积距平法和Mann-Kendall法突变检验

1956—2008 年年平均气温累积距平值呈现出先下降后上升的趋势：1956—1993 年呈下降趋势，1993—2008 年呈上升趋势，说明渭河流域宝鸡段年平均气温经历了下降—上升过程，气温突变可能发生在1993 年左右，如图1(a)所示.UF—UB曲线1993 年在临界线U0.05=1.96范围内有交点，且UF曲线超过了临界线，说明年平均气温在1993 年发生了由低到高的突变，如图1(b)所示.四季气温累积距平和M-K突变检验结果见表1.

图1 年平均气温累积距平曲线和M-K突变曲线Fig.1 The curve of cumulative anomaly method and Mann-Kendall method of the annual mean temperature

气温时段M-K法累积距平法 滑动T检验法5 年 7 年 10年 Yamamoto法5 年 7 年 10年 综合分析结果年平均1993199319931993,1994,19961992,1993,1994,1995,1996,199719941993,19941993,19941993,1994 春季19961993—1993,19961993—199319931993夏季—1975,1995—19931974,1975,1990,1992,1993,19941993——1975,1993秋季19861986——————1986冬季19871976,1987——————1987

1956—2008 年年降水量累积距平值呈现出波动上升再下降的趋势，1992 年达到累积最大值，气温突变可能发生在1992 年左右，如图2(a)所示.UF—UB曲线在1990 年有交点，说明年平均降水量在1990 年左右有波动，但UF，UB值均未超过0.05临界线(U0.05=1.96)，不存在突变现象，如图2(b)所示.四季降水量的累积距平和M-K突变检验结果见表2.

图2 年降水量累积距平曲线和年降水量累积距平曲线Fig.2 The curve of cumulative anomaly method and Mann-Kendall method of the annual precipitation

降水时段 M-K法 累积 距平法滑动T检验法5 年 7 年 10 年Yamamoto法 5 年 7 年 10 年综合分析结果年—19921992—19921992——1992春季1993,1997,1999,2002,20031962,1991,20001991——1991,1992——1991,2000夏季—1962,1979,199319621962,196319741962——1962秋季—1961,1975,1984———————冬季—1986,1998———————

注：1) 多年平均降水量为659 mm，1992年降水量有所偏离.

3.2 滑动T检验

利用滑动T检验法对渭河流域宝鸡段1956—2008 年年平均和四季气温、降水量时间序列进行突变分析.分析取n1=n2=5，n1=n2=7，n1=n2=10，取信度α=0.01，查表得显著性水平tα依次为3.355，3.055，2.878.1956—2008 年气温和年降水量滑动T检验曲线分别如图3，4所示.图3(a～c)和图4(a～c)分别对应n1=n2=5，n1=n2=7，n1=n2=10，图3，4中虚线表示0.01显著水平.四季气温和降水量滑动T检验结果，如表1，2所示.

图3 年平均气温滑动T检验曲线Fig.3 The MTT curve of the annual mean temperature

由图3可知：n1=n2=5时，年平均气温在1993 年发生升高突变；n1=n2=7时，年平均气温时间序列突变发生在1993—1996 年左右；n1=n2=10时，年平均气温时间序列突变出现在1992—1997 年左右.

由图4可知：n1=n2=5时，年降水量在1992 年发生了减少突变；n1=n2=7时，检验曲线没有超过信度临界线，降水没有发生突变；n1=n2=10时，在1992 年降水发生了减少突变.

3.3 Yamamoto检验

分别取n1=n2=5，n1=n2=7，n1=n2=10，选取信度α=0.01，对渭河流域宝鸡段1956—2008 年年平均和四季气温、降水量时间序列进行突变分析.年平均气温和年降水量Yamamoto检验曲线见图5，6.图5(a～c)和图6(a～c)分别对应n1=n2=5，n1=n2=7，n1=n2=10，四季气温和降水量Yamamoto检验结果，如表1，2所示.

图4 年降水量滑动T检验曲线Fig.4 The MTT curve of the annual precipitation

图5 年平均气温Yamamoto检验曲线Fig.5 The Yamamoto method curve of the annual mean temperature

图6 年降水量Yamamoto检验曲线Fig.6 The Yamamoto method curve of the annual precipitation

由图5可知：n1=n2=5时，年平均气温在1993年发生突变；n1=n2=7和n1=n2=10时，在1993，1994 年发生突变.由图6可知：n1=n2=5时，年降水量在1993 年发生突变1992 年；n1=n2=7和n1=n2=10时，年降水量时间序列都未检测出突变.

4 突变检验综合分析

结合累积距平法、Mann-Kendall法、滑动T检验法以及Yamamoto法对渭河流域宝鸡段1956—2008 年年平均与四季气温、降水量时间序列进行突变分析，为了保证突变点检验的准确性和可信度，将四种突变方法结合起来进行综合分析[14-15]，至少两种方法同时显示出突变则判定为突变点，分析结果如表1，2所示.

由表1可知：年平均气温时间序列在1993—1994 年间发生增高突变；春季气温在1993 年发生增高突变；夏季气温在1975 年发生降低突变，1993 年发生增高突变；秋季气温在1986 年发生增高突变；冬季气温在1987 年发生增高突变.由表2可知：年降水量时间序列在1992 年发生减少突变；春季降水量在1991，2000 年发生减少突变；夏季降水量在1962 年发生增多突变；秋季和冬季检验结果不突出，无法证明发生突变.

5 结 论

通过对渭河流域宝鸡段1956—2008 年气温和降水量的变化特征分析得出：1975 年夏季气温发生降低突变；1986—1987 年间，秋季和冬季气温发生增高突变；1993—1994 年间，年平均、春季和夏季等气温发生了增高突变.1962 年夏季降水量在发生增多突变；1991—1992 年间年降水量和春季降水量都发生减少突变；2000 年春季降水量发生减少突变.应用累积距平法、Mann-Kendall趋势检验法、滑动T检验法和Yamamoto法进行突变检测时，得出的结果不尽相同，所以在实际应用中，应采用多种方法相结合，这样即说明了出现突变的时间，又可以印证突变时间的准确性.

参考文献：

[1] 刘战胜,郭星火.宝鸡市水资源特征[J].水利科技,2008(4):20-21.

[2] 刘佳嘉.变化环境下渭河流域水循环分布式模拟与演变规律研究[D].北京：中国水利水电科学研究院,2013.

[3] 刘政鸿.陕西省近50年来降水量时空变化特征分析[J].水土保持研究,2015(2):107-112.

[4] 苏贺,康卫东,曹珍珍,等.1954—2009年窟野河流域降水与径流变化趋势分析[J].地下水,2013(6):14-17.

[5] 马瑞婷,黄领梅,沈冰.秦岭北麓典型流域年径流序列的突变分析[J].水资源与水工程学报,2016(2):76-79.

[6] 胡刚,宋慧.基于Mann-Kendall的济南市气温变化趋势及突变分析[J].济南大学学报(自然科学版),2012(1):96-101.

[7] SHENG Yue,PILON P,CAVADIAS G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series[J]. Journal of hydrology， 2002，264(1/2/3/4):262-263.

[8] 刘俊萍,周俊杰,王玮,等.渭河流域陕西段气象水文要素变化特征分析[J].浙江工业大学学报,2017,45(3):253-258.

[9] 丁爱中,赵银军,郝弟,等.永定河流域径流变化特征及影响因素分析[J].南水北调与水利科技,2013(1):17-22.

[10] 吕琳莉,李朝霞.雅鲁藏布江中下游径流变异性识别[J].水力发电,2013(5):12-15.

[11]YAMAMOTO R,IWASHIMA T,SANGA N K. Climatic jump,a hypothesis in climate diagnosis [J].Journal of the meteorogy society Japan,1985,63:1157-1160.

[12] ZHOU Yuanyuan,SHI Changxing,DU Jun,et al. Characteristics and causes of changes in annual runoff of the Wuding river in 1956—2009[J].Environmental earth sciences,2013,69(1): 225-234.

[13] 周园园,师长兴,杜俊,等.无定河流域1956—2009年径流量变化及其影响因素[J].自然资源学报,2012(5):856-865.

[14] 翁国庆,王强,黄飞腾,等.配电网络电压暂降源自动定位与智能识别[J].浙江工业大学学报,2016,44(1):45-51.

[15] 赵小敏,孙志刚,夏明.基于局部学习的车辆图像识别方法[J].浙江工业大学学报,2017,45(4):439-444.