注塑车间集成单元布局智能建模与关联优化
2018-07-06,,,,
,,,,
(浙江工业大学 机械工程学院,浙江 杭州 310014)
车间内设施和设备的布局状况影响车间加工生产的物流路径.注塑车间由于其设备体型大、重量重等特点,设备布局不合理往往会产生大量搬运物流成本和搬运时间,很大程度影响车间生产效率[1].目前大部分注塑车间布局仍然按照机群式布置,生产现场的物流路线变得混乱,容易出现交叉回流,不易降低物流成本.针对这类注塑车间,提出注塑车间基本布局原则,通过构建集成单元布局智能模型研究注塑车间布局,合理规划车间布局,降低物流浪费,提高生产效率.
目前国内外关于车间布局求解多采用智能算法建模解决此类多目标优化问题.文献[2]加入二维向量表达车间设备连续空间,通过设定加速系数和惯性系数,优化提高粒子群算法的寻优质量;文献[3]为解决设备形状固定,面积不等的设备多行布局问题,提出自由换行策略,改进自适应遗传算法,完成算法中变异概率和交叉概率非线性自动调整,增进求解的稳定性;文献[4-5]将差分演化策略结合元胞多目标算法,设计差分元胞多目标遗传算法对车间模型进行求解,大大提高算法收敛速度;文献[6]采用带轮盘赌选择算子,设计基于结构化编码的分散收索算法以此求解布局问题模型,提升求解速度和准确性;文献[7]结合启发式算法和粒子群算法,设计启发式人造粒子群优化算法解决车间布局问题,提高搜索效率;文献[8-10]利用自组织演化规则,构建多态性作业车间布局模型,并利用遗传元胞算法,求解车间布局最优解.笔者优化传统单元系统布局,合并单元构建和单元内布局过程,根据不同模型特点,分别设计结构化染色体多变异策略遗传算法对注塑车间单元构建和单元内布局集成设计模型进行求解,同时考虑生产计划变动下对车间布局的关联影响,设计实数编码多点交叉遗传算法进行求解.
1 注塑车间单元构建和单元内布局集成设计建模
1.1 注塑车间布局原则
注塑生产为非连续的离散性加工,不同型号的机台可以使用同种型号的模具,注塑件在生产加工时加工柔性较大,每台注塑机可以使用很多种不同的模具,但是不同注塑机使用不同模具和加工不同注塑件时的加工时间不同.注塑车间布局时需考虑车间面积限制,应采用直线多行布局,确保布局方案实施的实际可用性.
注塑成型工艺在一个或几个机台上加工完成,固定的单条流水线不能满足多品种产品需求.单元式布局基本的组成要素是零件族和设备族等.车间的生产系统被分为几大类零件族,其中每个零件族包含了其下属的各种加工零件,每个独立的零件族都被分配在某一个加工单元之中,加工车间就是由这些小的制造单元构建而成.这种布局模式可以在每一个小的制造单元内进行产品的流水线操作.单元式布局吻合注塑车间工艺,符合车间面积限制上的布局要求,最小化单元间和单元内的物流成本,降低总成本,提高生产效率.单元式布局从工艺要求和建模要求方面都切合注塑车间布局.
1.2 单元式布局系统设计
在传统的单元系统布局中,单元构建和单元内设备布局是独立两部分分别进行,而单元构建在单独进行设计时没有考虑单元间物流成本.笔者在单元式布局设计中,将单元构建和单元内布局综合同时完成,在计算单元构建时物流成本的同时完成单元内布局问题研究规避了单独设计单元构建时没有考虑单元间物流成本,影响最后车间成本结果,如图1所示.

图1 单元式布局结构图Fig.1 Unit layout structure
这种单元构建和单元内设备布局的集成处理具有优势:1) 基于产品加工工艺,更改模型参数,自动得到单元内设备布局;2) 单元构建与单元内设备布局组合求解,提升求解效率.
1.3 单元构建和单元内布局集成设计模型
注塑车间机台在加工过程中,将对应产品族所需原材料和模具设置在同一生产单元内能使物流搬运成本最小.一个生产单元构成分为3 部分:模具区、原料区和机台.综合考虑模型求解实际,单元构建做如下假设:1) 同一生产单元内注塑机台可以使用该单元生产产品所需的所有模具;2) 在一个生产单元内,原材料区,注塑机台和模具区之间按照直线单行排列;3) 一个系列的零部件只能在一个生产单元内进行加工;4) 在注塑成形过程中,已确定各原料工艺细节,并在一个单元加工中保持稳定,而且这种原料在车间生产中只生产某一种零件;5) 每台注塑机每次只能加工一种零部件,直到这种零件满足需求批量;6) 在原材料区中,所有零部件所需的原材料已经按照原料颜色分类完成;7) 忽略注塑机换模具时间,只考虑模具搬运成本.
单元构建问题描述:一个注塑车间有给定的M台注塑机,N种加工模具以及P种相应原料,原料生产批量为Vp,已知每种原料可以选择Rp种加工路线,每个注塑机只能加工一种原料,一种原料经过一台注塑机加工后就不需要经过下一台机器.为了优化制造流程,将P种原料分为F品类(分别加工不同种类产品),将M台注塑机分布在C个生产单元内,每个单元还设置一个原料区和一个模具区,模型的意义是使单元内物流、单元间物流及单元内机台换模具等成本最低.
1.4 多目标函数
注塑车间多目标布局需要考虑单元内物料搬运、单元内模具搬运、单元间物料搬运以及单元间模具搬运等成本.
针对注塑车间单元构建和单元内布局集成设计布局模型,可构建多目标函数指标.
1.4.1 单元内物料搬运成本Costp′和Costq′
1) 物流量wgm为
(1)

(2)

3) 根据式(1,2)可推导出Costp′,Costq′分别为
(3)
(4)
式中:Costp′为正常情况下单元内物流费用;Costq′为因质量问题造成的单元内物流费用.
1.4.2 单元内模具搬运费用Costh′
1) 换模物流量whm为
(5)

(6)
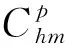
3) 根据式(5,6)可推导出Costh′为
(7)
式中Costh′为单元内模具搬运费用.
1.4.3 单元间搬运费用
当单元尺寸和单元数目在一定数值范围内变化时,单元间的物流费用趋近于一个稳定的最优常量.为了计算简便,在单元构建未完成的情况下,采用常量表示单元间物流费用.
(8)

(9)
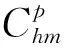
1.4.4 单元构建数学模型
综上所述,单元构建数学模型目标函数包括:单元内和单元间原料搬运费用;单元内和单元间模具搬运费用;单元内因质量问题产生的原料回流费用.
1) 无质量状况时单元内和单元间单位物流量搬运费用Costp为
(10)
式中:xgc为原料g是否属于单元c的决策变量;xmc为设备m是否属于单元c的决策变量.则其物流费用为
(11)
式中Costp为无质量状况时单元内和单元间单位物流量搬运费用.
2) 出现质量状况时单位物料搬运费用Costq为
(12)
则其物流费用为
(13)
式中Costq是出现质量状况时单位物料搬运费用.
3) 当机台需要换模时,单元内和单元间的单位物流搬运费用为
(14)
式中xhc为模具区h是否属于单元c的决策变量. 则其物流费用为
(15)
式中Costh为换模产生的物流费用.
4) 单元构建多目标函数为
F=Min(w1Costp+w2Costh+w3Costq)
(16)
式中:w1,w2,w3为各自子目标的权重值,w1,w2,w3∈[0,1],w1+w2+w3=1.
1.5 约束条件
多目标函数所包含的约束条件为

(17)

(18)

(19)
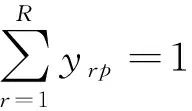
(20)

(21)

(22)

(23)
zgj+zhj+zmj=1 ∀j=1,2,…,J
(24)
约束条件中:式(17)限定一台设备只能属于一个单元;式(18)限定一个原料区只能属于一个单元;式(19)限定一个模具区只能属于一个单元;式(20)限定一个产品只能选择一条工艺路线;式(21)限定一个单元至少包括一个机台,只有一个原料区,只有一个模具区;式(22)限定一个位置只能放置一个机台或者一个原料区或一个模具区;式(23)限定一个机台或者原料区或模具区只能布置于一个位置;式(24)限定一个位置上各个区域不会重合.
2 结构化染色体多变异策略遗传算法求解
根据注塑车间特点,需要改进遗传算法进行求解.在染色体编码中染色体需要清晰地表示出设备-位置关系、设备-单元分组和工艺流程选择.笔者采用结构化编码方法,在设备-位置编码串中设计一个0,1二进制编码串确定设备单元分组位置,注塑车间单元构成包含加工机台、原料区和模具区,另外设立2 条二进制编码串对原料区和模具区在单元内的位置进行确定,第5 条编码串对每种原料的加工工艺选择进行表述.对于不同的染色体串采用不同的变异策略使得解的搜索符合客观实际.
2.1 获取初始种群
使用GA初始参数设定中的种群数量来确定初始种群的数量,根据种群数量创建相应的染色体数量,获取初始种群.
2.2 染色体编码策略
设备-位置编码串:设定一个长度为M(设备区,原料区,模具区个数)的编码串,其中每个基因位表示一个区域的编号.
单元分割编码串:设定一个长度为M-3的编码串,以此表示每个加工单元分割的基因点位.
原料区确定编码串:设定一个长度为M的二进制编码串,基因位为1时指示的就是设备-位置编码串中的原料区位置,基因位为0时表示该位置不是原料区.
模具区编码串:设定一个长度为M的二进制编码串,同理,基因位为1时指示的即是模具区的位置.
工艺路线选择编码串:设定一个长度为N(设备个数)的编码串,每个基因位对应单元中去掉原料区和模具区后每个设备的加工工艺编号,如图1所示.

图2 染色体编码策略Fig.2 Chromosome encoding strategy
2.3 适应度函数
单元构建模型是以单元内以及单元间物流成本来衡量,适应度函数可以取目标函数的倒数表示,适应度函数为
Fitness=10/Min(ω1Costp+ω2Costh+ω3Costq)
(25)
2.4 选择算子
使用轮盘赌运算,从当前个体周围任意选择2 个个体,被选择的可能性和个体适应度值成正比,个体被选择的概率为
(26)
式中:i为染色体编号;P为种群个体数量;Fiti为个体的适应度函数值.
2.5 交叉算子
采用单点交叉算法,对几条染色体串进行交叉,贴合单元分割点编码,模具区位置编码,原料区位置编码,工艺路线编码等染色体串的0,1二进制编码.在对二进制编码进行单点交叉时,只需交换选定的交叉点后的0,1.使用2 个父串进行示意,单点交叉算法如图3所示.

图3 单点交叉算法Fig.3 A single point of intersection algorithm
2.6 变异算子
对于设备-位置编码串,在一条染色体编码中随机选择2 个设备的编号,交换其在编码中的位置,得到新的染色体编码,如图4所示.

图4 设备-位置编码变异法则Fig.4 Coding equipment-position variation rule
对于单元分割编码串:由于是0,1二进制编码串,所以在其中随机选取一个基因位取相反的值,如图5所示.

图5 单元分割编码变异法则Fig.5 Cell segmentation encoding variation rule
对于工艺选择编码串:任意在染色体编码串上选择一个基因位,将其转变为任意一个随机的编码值,从而生成新的染色体串,如图6所示.

图6 工艺选择编码变异法则Fig.6 Process selection coding rule
对于原料模具判别编码串:由于在一个单元内分别只能有一个原料区和一个模具区,那么不能像单元分割编码的变异那样随机进行选择,在这里随机选择一个值为1的基因位,将1变为0后,在相邻的基因位上选择一个位置使其值变为1,从而生成新的编码串,如图7所示.

图7 原料模具区判别编码变异法则Fig.7 Raw materials mold area identifying code variation rule
2.7 结构化染色体多变异策略遗传算法求解流程
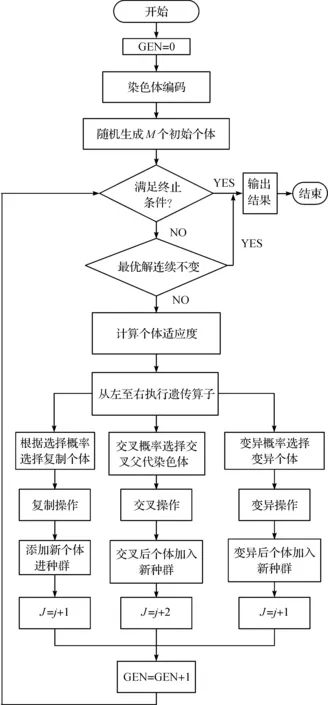
结构化染色体多变异策略遗传算法求解注塑车间单元构建和单元内布局集成设计模型,如图8所示.

图8 单元构建运算流程Fig.8 Unit constructing operation process
3 算例验证分析
为验证笔者提出的结构化染色体多变异策略遗传算法的有效性,现引用文献[2]中的算例作为对比算例,使用结构化染色体多变异策略遗传算法,对遗传算法和PSO算法进行对比验证.算法基本参数设置:种群数N=100,迭代代数T=500,交叉概率Pc=0.7,变异概率Pm=0.01.图9为笔者算法的仿真结果,表1为算法对比结果.
由表1可知:使用结构化染色体多变异策略遗传算法、PSO算法和常规遗传算法均可以在有效代数内得到最优结果.然而对比3 种算法发现:笔者结构化染色体多变异策略遗传算法收敛速度比其他2 种算法更快,寻优时间为0.23 s,同样最优适应度值更高,最后得到的物流搬运成本最低.从而证明结构化染色体多变异策略遗传算法在注塑车间布局中的有效性和优越性.

图9 结构化染色体多变异策略遗传算法迭代过程Fig.9 Structural chromosomal mutation strategy geneticalgorithm process

算法迭代代数最优适应度值物料搬运成本遗传算法1984.46×10-42 243.08PSO算法1764.47×10-42 239.37笔者算法1534.53×10-42 234.26
4 注塑车间单元系统布局与关联优化集成模型
4.1 单元系统布局关联优化集成模型分析
通过单元构建和单元内布局集成设计模型和结构化染色体多变异策略遗传算法求解下,得到单元式布局合理的单元个数,各个单元内机台的具体布置状况.在此基础上仍然需要考虑实际车间单元式布局中因机台状态或者生产计划变动等问题,出现物料和模具在单元间进行流动的状况,产生大量单元重置费用.在第一阶段模型求解下,进而考虑单元数量、单元尺寸、单元间的相对位置关系以及单元间原料的工艺联系对单元式布局的影响.在进行单元系统布局中将生产计划变动的关联性影响考虑进单元系统布局模型中,对布局模型进行关联性优化,使布局结果最大程度适应计划变动带来的关联性影响.
4.2 布局模型关联优化设计
生产计划变动所带来的关联性影响主要体现在物流费用的增加上,然而计划的变动是无法改变的,在单元布局时只能考虑在必要的物流搬运过程中减少物流费用.在集成设计模型中,除了原先设定的单元间物流费用,车间面积利用率这2 个目标函数之外,为了实现对模型的关联优化,引入了关联控制系数ACC,关联控制系数是指在某个因计划变动产生的原料流动过程中的物流费用波动率.车间内物流费用波动率在进行量化设计时,通过单元系统布局使得单元间物流费用波动率趋近某一针对个别车间特点设定的固定值,当关联控制系数趋近于这个最优百分比时,该布局所受的关联影响最小.关联控制系数和物流总成本以及车间面积利用率的关系曲线,如图10所示.

图10 关联控制系数关系曲线Fig.10 TheACC relation curve
单元间间距减少可以使得物流最小费用减少,从而可以满足单元系统布局模型中的总物流成本最低目标函数,但是这样就使得关联控制系数变得非常高,由此衍生的后果就是车间面积利用率变低.在物流费用曲线和面积利用率曲线中当2 条曲线相交时,对应的固定关联控制系数值为最优值.将这个关联控制系数作为单元系统布局的优化目标使其趋近于此最优值,使得出的单元式布局方案在面对计划波动带来关联性影响时将产生的物流费用在不更改单元布置的前提下达到最低化.
4.3 单元系统布局与关联优化集成模型
在进行单元系统布局与关联优化集成建模时需要做以下假设:1) 在进行单元系统布局前,生产单元构建已完成;2) 在进行单元系统布局前,单元内布局已经完成;3) 各个单元的面积和形状可以表示为矩形;4) 注塑车间中单元系统布局问题是一个多行直线布局问题.
4.4 多目标函数
在模型中使用如图11所示方式表示每个独立的生产单元的长、宽以及单元间距坐标正方向是各个生产单元具体坐标数值变大的方向,在这个区域中模型每个生产单元都可以使用正坐标进行表示.图11中:dmin,hmin分别为水平方向同一行内单元最小间距和垂直方向单元间的最小间距;x轴和y轴分别为车间的边界;L为长度;H为宽度.

图11 模型参数参考线示意图Fig.11 Schematic diagram of model parameters
1) 单元间物流费用为
(27)
式中:p为车间内各单元加工的各种物料;cpcc′为单元c和c′之间单位物流量以及单位距离物料搬运成本;wpcc′为物料p在单元c和c′之间的物流量;dcc′为单元c和c′之间的距离.
对于单元之间单位物流量单位距离的物料搬运成本一般布局研究中都设定为一个常量cpcc′,单元c和c′之间的物流量公式和1.4描述的相似.wpcc′为
(28)
考虑到车间内物料搬运路线不能按两点之间直线搬运,单元间的距离则视为单元间折线距离,即
dcc'=|xi-xj|+|yi-yj|
(29)
2) 车间面积利用率为
(30)
式中:Sc为各个单元在单元构建后形成的面积,Sc为单元系统布局完成后的单元总面积.其中Sc=lk(j)lk(j),Sc=HL.
3) 关联控制系数ACC为
(31)

(32)

(33)
设定关联性系数在趋近于一个指定值λ的情况下设施布局在计划变动时生产状况最为稳定.那么关联控制系数的目标函数为
Minθ=|ACC-λ|
(34)
单元系统布局和关联优化集成设计模型由方程式(27,30,34)的结果归一化后按照权重系数相加而得,其多目标函数模型为
F=Min{μ1w1cost+μ2w2(1-U)+w3θ}
(35)
式中:w1,w2,w3为各自子目标的权重值,w1,w2,w3∈[0,1],w1+w2+w3=1;μ1,μ2为总目标函数的归一化因子[11],归一化因子的作用是将在不同量纲下的子目标函数值转化为同一量纲,而且其值都趋近于1,归一化因子的表达方式为
(36)
经过子目标函数的归一化处理,就可以使几个子目标函数结合成一个总目标函数,可以去除子目标不在一个量纲下的问题.
4.5 约束条件
多目标函数求解所包含的约束条件为
xkj> 0,ykj> 0,k=1,2,…,K,j=1,2,…,J
(37)
(38)
(39)
(40)
(41)
(42)
(43)
(44)
λ=0.15
(45)
约束条件中:式(37)规定了同一行内的2 个单元不能相互重合;式(38,39)规定两行间行距不为零;式(40)规定了一个单元只能布置在一行内,一个单元只能被放置一次;式(41~44)为单元与车间之间的边界约束;式(45)为关联控制系数的合理值.
5 实数编码多点交叉遗传算法求解
5.1 染色体编码
在单元系统布局算法设计中采用实数编码的策略,染色体中每个基因位表达的是每个不同单元的横坐标和纵坐标序列.表达方式如下:将各个独立单元的中心坐标作为字符串,一个单元的横纵坐标为一组基因,如:(x1,y1,x2,y2,…,xi,yi),其中一组(xi,yi)为这条染色体的一个基因,表示的是单元i的中心横纵坐标,具体表示如图12所示.

图12 单元系统布局染色体编码Fig.12 Unit system layout chromosome coding
图12中单元1的坐标即为(1,2),单元2的坐标为(3,5),这种编码方式使得最优解的解码变得简单,最优结果中每个基因的数值即是每个单元在二维空间中布局的具体坐标,这种方法同时避免了讨论单元的间距问题,通过得出单元坐标直接显示单元布局.
5.2 初始种群生成
在进行遗传算法各种操作前,从随机解集区域中随机选取一组固定数量的染色体,以这一组染色体作为遗传算法的初代个体.通过计算这一组染色体的适应度来选择进行遗传操作的父代染色体,初始种群的选择是遗传算法中重要的初始环节,一般取100 个.
5.3 适应度函数
在单元系统布局设计中,取适应度函数的方法和单元构建时相似,为了使得求解结果更加准确,在这个适应度函数中需要加入惩罚系数,如果染色体满足约束条件则惩罚系数取0,否则惩罚系数取较大的正整数,适应度函数为
(46)
5.4 选择算子
采用的轮盘赌方法,第i条染色体的选择概率为
(47)
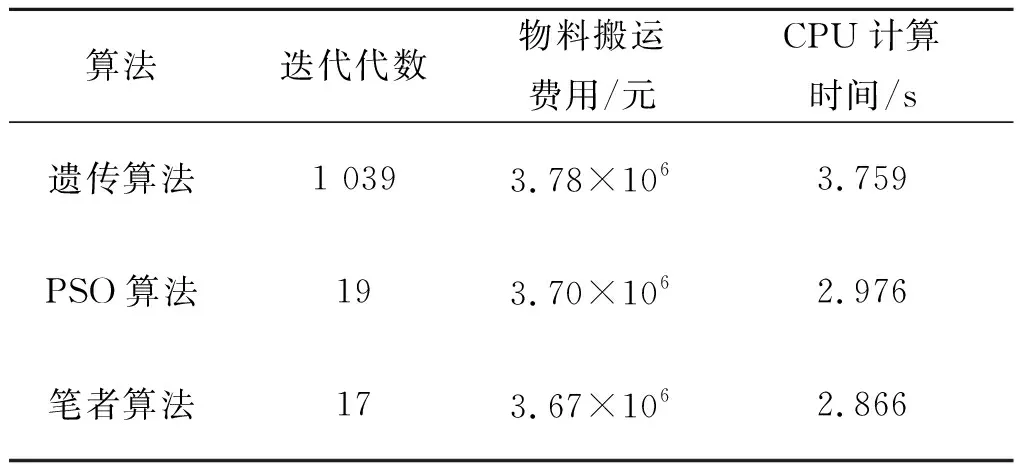
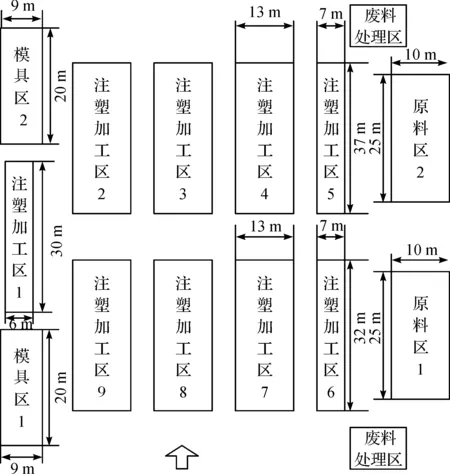
在轮盘赌方法中,轮盘将转动N次(初始种群的数量),每转动一次产生一个被比较的个体,该个体的选择概率将和一个随机产生的0~1之间的实数相比较,如果Pi-1 采取多点交叉的方法,在染色体中随机选择2 个基因位为交叉点,将交叉点之间的基因随机排列,然后对相邻的2 个基因位的值进行算术交叉,具体方法如图13所示. 图13 单元系统布局交叉原则Fig.13 Layout principle of unit system 算术交叉得到的子代染色体为 (48) 式中∂为一个随机数,∂∈(0,1). 系统布局模型的变异策略采用的随机单点变异的方法.通过随机在染色体串中选择一个基因位,进行变异操作,得到新的个体. (49) 式中的变异步长是一个固定值,一般取单元间的最小间距,每个单元中心的坐标通过变异步长的左右上下搜索,得到新的坐标位置. 该算法的运算流程如图14所示. 图14 单元系统布局关联优化模型运行流程图Fig.14 Flow chart of unit system layout optimization model 为验证笔者提出的实数编码多点交叉遗传算法的有效性,现在引用文献[11]中的算例进行对比算例,使用实数编码多点交叉遗传算法,对文献[12]中改进的遗传算法和PSO算法三者进行对比验证.算法基本参数设置:种群数N=100,迭代代数T=100,交叉概率Pc=0.6,变异概率Pm=0.01,在CPU为2.2 GHz,内存4 G的Window 7系统下进行操作.图15为笔者算法的仿真结果,表2为算法对比结果. 图15 实数编码多点交叉遗传算法迭代过程Fig.15 Real coded multi point crossover genetic algorithm 算法迭代代数物料搬运费用/元CPU计算时间/s遗传算法1 0393.78×1063.759PSO算法193.70×1062.976笔者算法173.67×1062.866 由表2可知:使用实数编码多点交叉遗传算法、PSO算法和遗传算法均可以在有效代数内得到最优结果.然而对比3 种算法发现:笔者实数编码多点交叉遗传算法迭代代数更少,在同等设备情况下CPU计算时间更快,最后得到的物流搬运成本最低.从而证明实数编码多点交叉遗传算法在车间布局中的有效性和优越性. 通过具体的实际例子,将模型算法应用于企业布局中,研究模型算法的实用性.F公司注塑车间可利用面积为70 m×60 m,注塑车间现在拥有机台50 台,2 个总原料区,2 个总模具区,布局现状如图16所示.通过单元构建得到在注塑车间内可设置12 个独立的生产单元,每个生产单元包含一个原料区,一个模具区和若干注塑机台,每个生产单元中的原料对应相应的加工工艺.注塑机尺寸为长2.5 m,宽1 m,每个单元原料区和模具区的尺寸按照实际包含的原料和模具决定. 取单元1为示例,则单元内区域布置如图17所示. 图16 布局现状图Fig.16 Workshop layout status 图17 单元1内布局Fig.17 Unit 1 within the cell layout 利用结构化染色体多变异策略遗传算法对参数进行设置为种群数N=100,迭代代数T=400,交叉概率Pc=0.8,变异概率Pm=0.01.利用实数编码多点交叉遗传算法对参数进行设置为种群数N=100,迭代代数T=100,交叉概率Pc=0.6,变异概率Pm=0.03.根据实际设定以下参数:CAP=1,CBP=1.5,CXP=5,CAh=8,Cij=10. 车间改善后布局如图18所示. 图18 注塑车间布局最优解Fig.8 Injection workshop layout optimization 由表3可知:应用笔者算法求解下,单元内物料搬运成本,发生质量问题下物料搬运成本和换模具过程物流成本均得到了大幅度的下降.经过改善后注塑车间布局得到优化,车间布局更加合理,物流更加通畅,侧面验证模型算法的实用性. 表3 改善前后目标函数值对比Table 3 Objective function values before and after contrast 单元式布局原则符合注塑车间特点,能够解决其他布局原则的局限性.根据注塑车间加工特点,在单元构建模型中,将单元分割和单元内布局同步进行,提高运算效率又使所得结果更加切合实际.以单元内和单元间原料搬运成本最低和模具搬运成本最低为目标函数,结合单元构建基本约束条件,建立了注塑车间单元构建和单元内布局集成设计模型,利用结构化染色体多变异策略遗传算法求解模型快速有效.同时考虑生产计划变动带来的关联影响,建立单元系统布局与关联优化集成模型,利用实数编码多点交叉遗传算法进行动态求解.由于篇幅所限,未对原料区和模具区展开形状讨论,在以后的工作中将加深这一方面的研究. 参考文献: [1] 刘毅兴.浅谈注塑车间基本布局[J].模具制造,2016(8):35-38. [2] 郭源源,王谦,梁峰. 基于粒子群优化算法的车间布局设计[J]. 计算机集成制造系统,2012,18(11):2476-2484. [3] 周娜,宓为建,徐子奇,等. 基于改进型自适应遗传算法求解设备多行布局问题[J].上海交通大学学报,2013,47(12):1924-1929. [4] 张屹,卢超,张虎,等. 基于差分元胞多目标遗传算法的车间布局优化[J]. 计算机集成制造系统,2013,19(4): 727-734. [5] CANYURT O E,HAJELA P. Cellular genetic algorithm technique for the multicriterion design optimization[J]. Structural and multidisciplinary optimization,2010,40(1/2/3/4/5/6):201-214. [6] 郑永前,钱伟俊,谢松杭. 基于模糊需求与机器产能的动态单元构建与布局问题[J]. 计算机集成制造系统,2014,20(7): 1561-1571. [7] CHAO OY,SANTOSA B,MUSTAKIM A.Artificial particle swarm optimization with heuristic procedure to solve multi-line facility layout problem[C]//Proceedings of the Institute of Industrial Engineers Asianconference.Singapore: Springer,2013:1431-1439. [8] 陈勇,阮兴聪,鲁建厦,等.基于元胞机和改进GA的大型零件柔性作业车间调度算法[J].中国机械工程,2012,23(21): 177-184,190. [9] 陈勇,阮兴聪,王亚良,等.基于元胞机的大型机械构件生产车间柔性调度求解[J].浙江工业大学学报,2011,39(4): 433-439. [10] 陈勇,王忠住,王亚良,等.基于遗传元胞机的多态性作业车间布局建模[J].浙江工业大学学报,2014,42(6): 676-681. [11] 魏书堤,李明志.基于TOPSIS的第三方物流综合评价方法[J].衡阳师范学院学报,2011,32(3): 76-79. [12] 马淑梅,蔡惠森,张一帆,等.不确定需求下的设备动态布局方法[J].中国机械工程,2015,26(11):1494-1502.5.5 交叉算法

5.6 变异算法
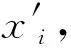
5.7 实数编码多点交叉遗传算法求解流程
6 算例验证分析

7 案例研究



8 结 论
