基于单亲遗传算法的作战体系击破策略

李国栋，刘娜，王鹏，陈健军

（中国电子科技集团公司电子科学研究院，北京 100041）

0 引言

随着信息技术的快速发展，作战理念正向基于效果的作战转变，作战方式朝着“网络中心战”的方向发展，参战力量的网络化越来越明显，体系对抗已成为当前和未来作战的主要形态[1]。

在体系对抗过程中，对抗的胜负不再以击毁、击毙敌方装备、人员的数量和百分比作为衡量指标，这是机械化战争的取胜标准。信息化条件下作战，是以谁先击破对方的作战体系，尽快将对方的体系作战力量摧毁，并且短时间内无法恢复，谁就取得了胜利。近几年的信息化局部战争都说明了这个问题，所以信息化条件下的体系对抗应当以体系作战能力削弱为目标，尽快击破对方的作战体系。

本文针对如何快速削弱体系作战能力的问题进行了数学描述，提出了一种基于单亲遗传算法的击破策略生成方法，并通过算例对所提方法进行了验证。

1 问题建模

1.1 作战体系抽象

作战体系由体系中功能各异的装备及装备间的复杂关系组成，是一个典型的复杂网络，可通过装备之间的作战关系所构成的整体加以描述。利用节点和边分别对作战装备以及装备间的相互关系进行抽象，即可构建作战体系的网络化模型。

根据现代作战循环理论，作战活动是一个侦察、决策、行动的循环过程，可用作战环加以表述。作战环是针对特定作战任务，由作战体系中的感知、决策、攻击等武器装备实体与敌方目标实体构成的有作战行为关系的闭合回路[2]。如图1所示，环中各类节点之间的有向边是节点之间作战关系的抽象，涉及基于红外、电磁、光波等形式的感知能量流；基于无线电、有线通信线路等载体的决策支持信息流和指控信息流；以及基于火力打击过程而建立起来的攻击能量流。作战环代表了作战活动的最简单基本环节，称作标准作战环（Standard Operation Loop）[3]。

因此，本文将单方的作战单元抽象为感知S、决策D、攻击A三类节点并引入目标节点T，通过作战环来进行作战关系的抽象描述。

1.2 体系作战模型

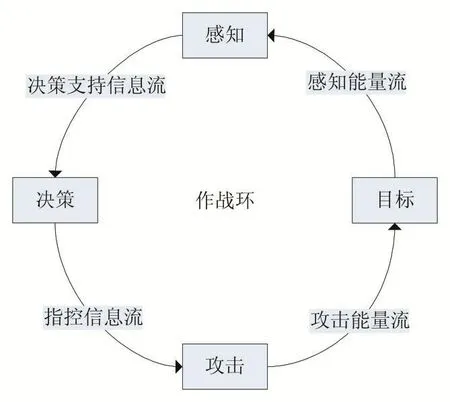
图1 标准作战环

为了量化反映作战体系的装备能力及装备之间的关系，本文采用矩阵的形式来进行模型描述。以图1所示的标准作战环为例，设感知、决策、攻击节点的能力度量分别是CS、CD和CA，支撑决策支持信息流和指控信息流的通信保障能力的度量分别是CSD和CDA，指定条件下感知节点和攻击节点适用于目标对象的适用度分别是CTS和CAT，则综合反映标准作战环中装备能力及关系的矩阵G为：

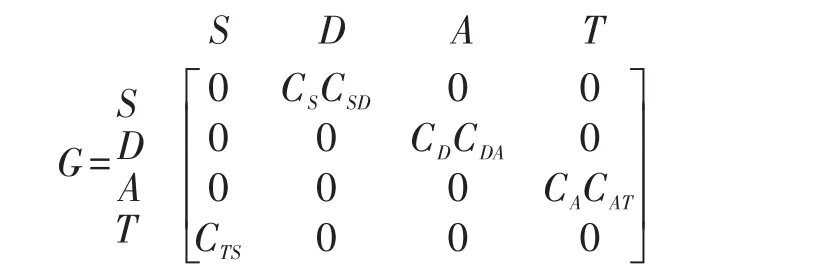
称为能力关系矩阵。其中，矩阵的第i行第j列若为非零元素，则表示第i行的节点对第j列的节点存在指向关系，若为零元素，则表示无指向关系或指向关系太弱可以忽略。关于各类节点的能力度量，目前已经有许多较为成熟的方法，在此，便不赘述。

1.3 体系作战能力

能力关系矩阵G是对武器装备体系作战模型的数学描述，反映了体系中装备间的关系与能力大小，而作战环作为作战活动的基本环节，其数量和质量在一定程度上反映了武器装备体系的作战能力，因此，可通过评价能力关系矩阵G中作战环的数量和质量的方式来度量武器装备体系的作战能力[4,5]。

当网络中包含的节点数目庞大、连接关系复杂时，精确计算作战环的数目、长度将导致计算量非常大。为了方便快捷地综合计算网络中作战环的数量、长度，本文利用作战环综合能力指数τindex_T来综合衡量体系中作战环的数量和质量。

其中，index_T为目标T在矩阵G中对应的行列序号，τindex_T表示作战体系中作战环对目标T的作战能力需求满足度的加权和，本文以此来表征作战体系在一定条件下对目标T的作战能力。

1.4 体系击破策略优化问题

体系击破问题的实质是通过寻找可行的节点攻击顺序，使得按照该顺序进行打击时体系作战能力快速下降为零，且这个过程中作战能力的平均水平最低。

假设某一作战体系由N个节点组成，其体系的能力关系矩阵为G，则该体系的击破策略优化问题可描述为如下数学模型：

其中，x为N维决策向量，其分量xi表示打击序列中第i个摧毁节点的标号，各分量的取值属于集合{1,…,N}且各不相同；G(x[1:k])表示从能力关系矩阵G中去除向量x中前k行对应标号的节点后的矩阵；f(G(x[1:k]))表示经过k次打击后作战体系的作战能力，本文选择作战环综合能力指数作为f(·)，具体应用时函数f(·)可根据不同的作战体系进行调整。问题的优化目标是使每次打击后作战体系的剩余作战能力之和最小。

2 基于单亲遗传算法的击破策略优化

遗传算法模拟生物基因的遗传进化过程，通过编码组成初始种群后，按照种群中染色体对环境的适应程度施加一定操作，从而实现种群的进化。主要包括初始种群生成、适应度计算、遗传操作三个主要环节。

2.1 初始种群生成

在体系击破策略的优化求解中，本文采用序号编码方式，将染色体定义为节点的先后摧毁序列，用没有重复数字的向量x表示，同决策向量。例如，某个体系由标号分别为 1、2、3、4、5、6 的节点组成，那么，摧毁序列 3＞1＞5＞2＞4＞6 则可用染色体x=(3,1,5,2,4,6)T进行表示，其分量为摧毁节点的标号。

根据以上编码规则，种群中的每一个染色体都是N个节点的一个排列，随机生成m个1～N的随机排列，即可得到m个染色体的初始种群，m为种群数量。

2.2 适应度计算

该问题的优化目标是最小化目标函数考虑到遗传算法追求适应度较大的个体，所以定义适应度函数为：

2.3 遗传操作

体系击破问题的本质为排序问题，若用传统的遗传算法进行求解，在完成交叉操作后，需要附加大量的修正操作来保证染色体的可行性。因此，本文采用单亲遗传策略，通过用单条染色体的遗传操作取代两条染色体之间的交叉操作，来克服传统算法的不足。不但有利于提高搜索效率，而且不要求初始群体的多样性，不易出现早熟现象。

本文主要采用以下三种基因重组的方式来进行单亲遗传操作。

（1）基因换位

基因换位是以一定的概率pe把一条染色体上的上的基因进行位置互换，被交换的位置是随机的。

根据交换基因对的数量，可分为单点换位和多点换位。单点换位是一次只交换一对基因的位置，如图2所示。多点换位是对预先给定的阈值ue，取随机数i(1≤i≤ue)，一次交换i对基因，如图3所示。

图2 单点换位

图3 多点换位（ue=3,i=2）

（2）基因移位

基因移位是以一定概率ps把一条染色体上的上的一些基因段依次向后移动，并把基因段段尾的基因移到原基因段段首的位子上。基因段的长度和位置也都是随机确定的。

基因移位也分为单点移位和多点移位。单点移位是在一条染色体中只取一个子串作基因移位操作，如图4所示；而多点位移是对预先给定的正整数us，先取随机数i(1≤i≤us)，然后在一条染色体中取i个子串作基因移位操作，如图5所示。

图4 单点移位

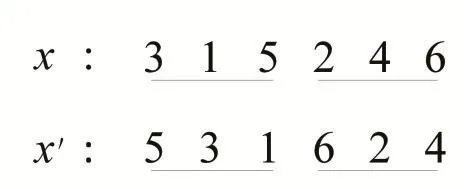
图5 多点移位（us=3,i=2）

（3）基因倒位

基因倒位是以一定概率pi把一条染色体上的一些基因段依次倒转。基因段的长度及位置也是随机确定的。

基因倒位可分为单段倒位和多段倒位。单段倒位是在一条染色体中只取一个子串作基因倒位操作，如图6所示；而多段倒位是对预先给定的正整数ui，先取随机数i(1≤i≤ui)，然后在一条染色体中取i个子串作基因倒位操作，如图7所示。

图6 单段倒位

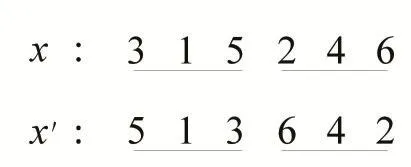
图7 多段倒位（ui=3,i=2）

上述遗传操作可根据问题求解需要进行适当的选择与调整。当染色体的长度N很大的时候，一般使用多点遗传操作，而当N很小的时候，适合使用单点遗传操作。在遗传迭代初期，尤其是当初始群体不具有广泛多样性时，宜用多点遗传操作；而在遗传迭代后期，一般用单点遗传操作。

2.4 算法步骤

（1）参数设置。设置种群的染色体数量M，遗传操作 参 数 pe、ps、pi、ue、us、ui，以 及 最 大 进 化 代 数maxGen等。

（2）初始种群生成。随机生成具有M个染色体的种群。

（3）适应度计算。利用式（2）计算染色体 Xi(1≤i≤M)的适应度F(Xi)。

（4）遗传操作。对上一代种群中的染色体按概率进行基因换位、基因移位、基因倒位操作，产生新染色体。

（5）评价新染色体。计算新染色体的适应度。

（6）终止条件判断。若达到最大进化代数，或者最大适应度的改善幅度连续r代小于tol，则输出最优解并停止，否则，进入下一步。

（7）生成下一代种群。从上一代种群中的染色体和本次遗传操作所产生的新染色体中，按照染色体适应度的比例，使用轮盘赌的方式，选择出M个染色体构成下一代种群，转步骤（4）。

3 算例验证

为了验证所提方法，本文以如图8所示的作战体系为例进行击破策略计算。

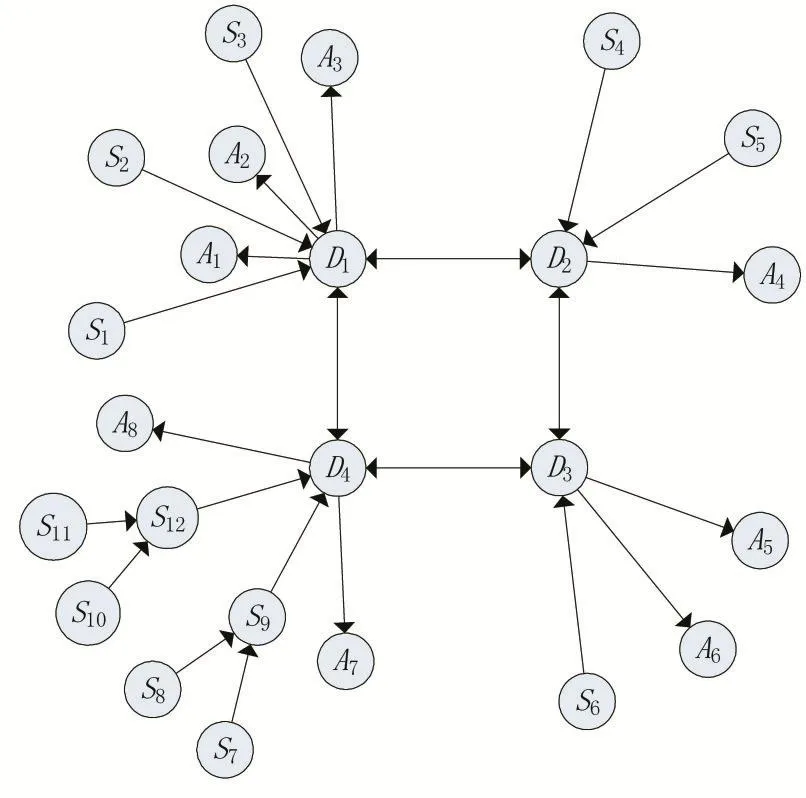
图8 作战体系示意图

假设作战体系中指挥节点D1和D2控制的感知和攻击节点能力归一化度量为0.7，其他感知、决策、攻击节点的能力均为0.9，节点间的通信保障能力为1，且目标节点符合感知和攻击节点的适用范围。

在算法参数设置上，取种群规模M=50，最大进化代数maxGen=300，遗传操作参数pe、ps和pi分别设置为 0.5、0.4、0.1，而阈值 ue、us和 ui在 1～100 次迭代时取 3，在 101～200次迭代时取 2，在 201～300次迭代时取1。

计算结果与随机攻击、度大攻击策略的对比如下。

表1 不同策略的攻击结果对比

图9 不同策略的击破效果对比

三种策略的击破效果对比如图9所示。可以看出，本文所提出的策略算法，与随机攻击、度大攻击相比具有更好的体系击破效果，体现所提方法的有效性。

4 结语

本文面向体系作战中科学合理的决策需要，针对作战体系的击破问题开展研究，通过对作战体系及其能力的抽象描述，建立了体系击破问题的数学模型，提出了基于单亲遗传算法的击破策略优化算法。经过算例验证，本文所提算法比随机攻击策略、度大攻击策略具有更好的体系破击效果，表明了算法的有效性。

[1]杨克巍,赵青松,谭跃进,等.体系需求工程技术与方法[M]．北京:科学出版社，2011.

[2]赵丹玲,谭跃进,李际超,等.基于作战环的武器装备体系贡献度评估[J].系统工程与电子技术,2017,39（10）:2239-2247.

[3]Sean Deller,Ghaith Rabadi,Andreas Tolk,et al.Organizing for Improved Effectiveness in Networked Operations[J].Military Operations Research,2012,17（1）:5-16.

[4]马力,张明智.作战体系网络化效能仿真分析方法[J].系统仿真学报,2013,25（S）:301-305.

[5]谭跃进,张小可,杨克巍.武器装备体系网络化描述与建模方法[J].系统管理学报,2012,21（6）:781-786.